euler calculus data robert ghrist university of pennsylvania

euler calculus & data robert ghrist university of pennsylvania depts. of mathematics & electrical/systems engineering

motivation
tools
euler calculus
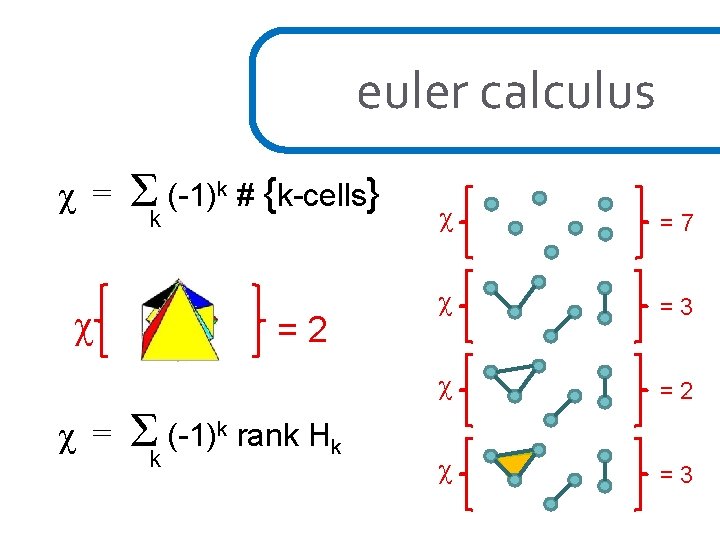
euler calculus χ = χ χ = Σk (-1)k # {k-cells} =2 Σk (-1)k rank Hk χ =7 χ =3 χ =2 χ =3

sheaves
![lemma: [classical] χ(Au. B) = χ(A)+ χ(B) – χ(A B) u lemma: [classical] χ(Au. B) = χ(A)+ χ(B) – χ(A B) u](http://slidetodoc.com/presentation_image_h2/e010c2f15ff98d69c116c37e2bdb864c/image-7.jpg)
lemma: [classical] χ(Au. B) = χ(A)+ χ(B) – χ(A B) u
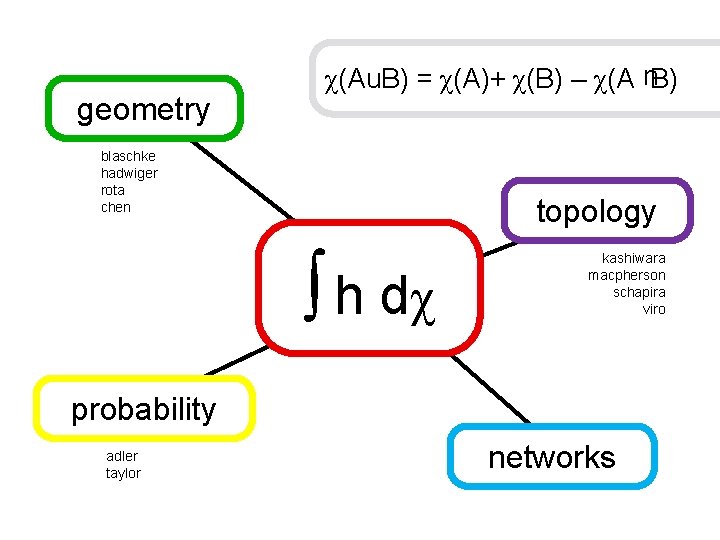
u geometry χ(Au. B) = χ(A)+ χ(B) – χ(A B) blaschke hadwiger rota chen topology ∫ h dχ kashiwara macpherson schapira viro probability adler taylor networks

integration consider the sheaf of constructible functions results tools CF(X) = Z-valued functions whose level sets are locally finite and “tame” axiomatic approach to tameness in the work on o-minimal structures collections {Sn}n=1, 2, . . . of boolean algebras of sets in Rn closed under projections, pr elements of {Sn}n=1, 2, . . . are called “definable” or “tame” sets all definable sets are triangulable & have a well-defined euler characteristic all functions in CF(X) are of the form h = Σci 1 U for Ui definable i all functions in CF(X) are integrable with respect to Euler characteristic explicit definition: euler integral ∫ h dχ = ∫ (Σ ci 1 Ui) dχ= Σ(∫ ci 1 Ui)dχ= Σci χ(Ui)
![integration [schapira, 1980’s; via kashiwara, macpherson, 1970’s] the induced pushforward on sheaves of constructible integration [schapira, 1980’s; via kashiwara, macpherson, 1970’s] the induced pushforward on sheaves of constructible](http://slidetodoc.com/presentation_image_h2/e010c2f15ff98d69c116c37e2bdb864c/image-10.jpg)
integration [schapira, 1980’s; via kashiwara, macpherson, 1970’s] the induced pushforward on sheaves of constructible functions is the correct way to understand dχ X CF(X) F F* Y CF(Y) pt X in the case where Y is a point, CF(Y)=Z, and the pushforward is a homomorphism from CF(X) to Z which respects all the gluings CF(X) CF(pt)= implicit in sheaves. . . ∫ dχ Z F pt X Y corollary: [schapira, viro; 1980’s] fubini theorem CF(X) F* CF(Y) CF(pt)= ∫ dχ Z sheaf-theoretic constructions also give natur convolution operators, duality, integral trans. . .
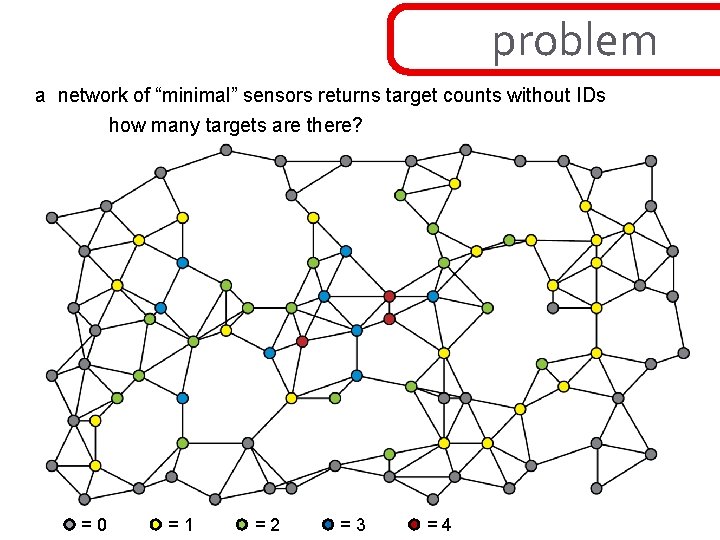
problem a network of “minimal” sensors returns target counts without IDs how many targets are there? =0 =1 =2 =3 =4
problem
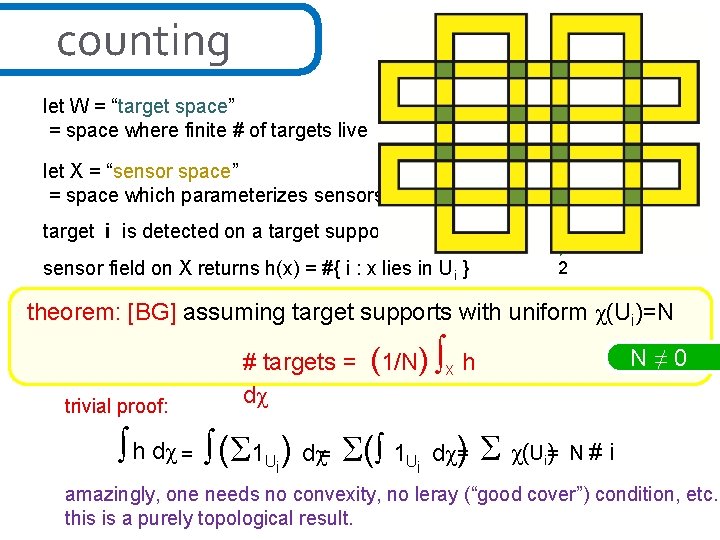
counting let W = “target space” = space where finite # of targets live let X = “sensor space” = space which parameterizes sensors target i is detected on a target support Ui in X h: X→Z sensor field on X returns h(x) = #{ i : x lies in Ui } 2 theorem: [BG] assuming target supports with uniform χ(Ui)=N trivial proof: # targets = dχ (1/N) ∫X h N≠ 0 ∫ h dχ = ∫ (Σ 1 Ui) dχ= Σ(∫ 1 Ui dχ)= Σ χ(U )= i N# i amazingly, one needs no convexity, no leray (“good cover”) condition, etc. this is a purely topological result.

computation for h in CF(X), integrals with respect to dχ are computable via ∞ ∫ h dχ = s=0 Σ s χ({ h=s }) level set ∞ = s=0 Σ χ({ h>s })-χ({ h<-s }) = ΣV h(V)χ(v) “chambers” of h components of level sets upper excursion set weighted euler index
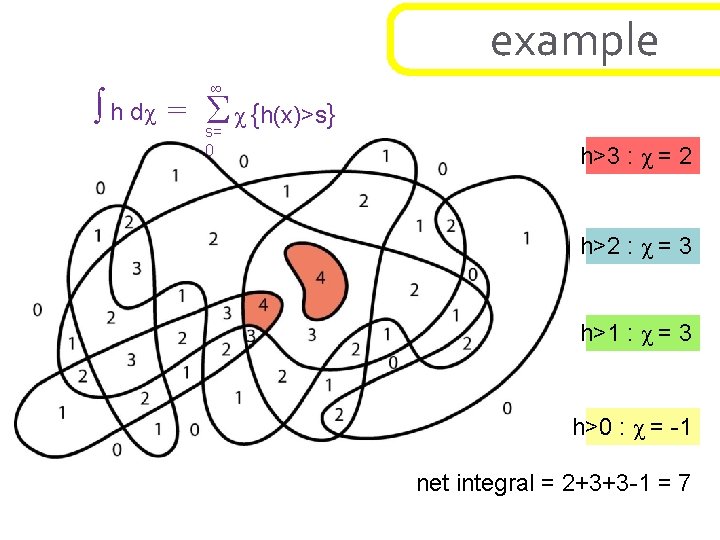
example ∞ ∫ h dχ = s=Σ χ {h(x)>s} 0 h>3 : χ = 2 h>2 : χ = 3 h>1 : χ = 3 h>0 : χ = -1 net integral = 2+3+3 -1 = 7
some applications in minimal sensing

waves consider a sensor modality which counts each wavefronts and increments an internal counter: used to count # events 3 booms… whuh? 2 booms… the resulting target impacts are still nullhomotopic (no echoing) curate event counts obtained via ad hoc network of acoustic sensors with no clocks, no synchronization, and no localization 17
wheels consider sensors which count passing vehicles and increment an internal counter acoustic sensors embedded in roads… such target impacts may not be contractible… theorem: [BG] if sensors read h = the total number of time intervals in which some vehicle is nearby, then # vehicles = ∫ h dχ
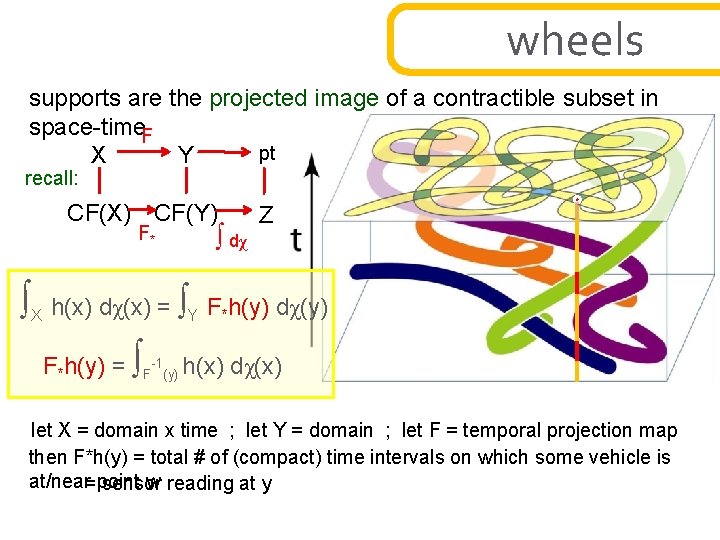
wheels supports are the projected image of a contractible subset in space-time. F pt X Y recall: CF(X) CF(Y) F* ∫ X ∫ dχ Z h(x) dχ(x) = ∫Y F*h(y) dχ(y) F*h(y) = ∫ -1 F (y) h(x) dχ(x) let X = domain x time ; let Y = domain ; let F = temporal projection map then F*h(y) = total # of (compact) time intervals on which some vehicle is at/near= point w reading at y sensor

numerical integration
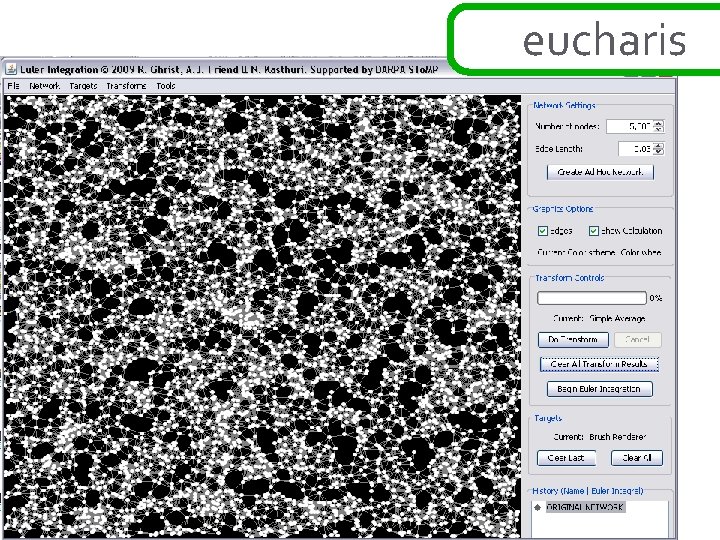
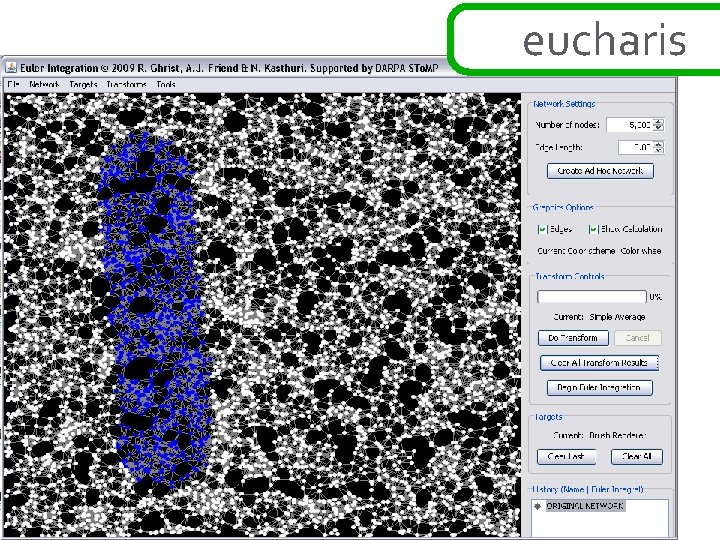
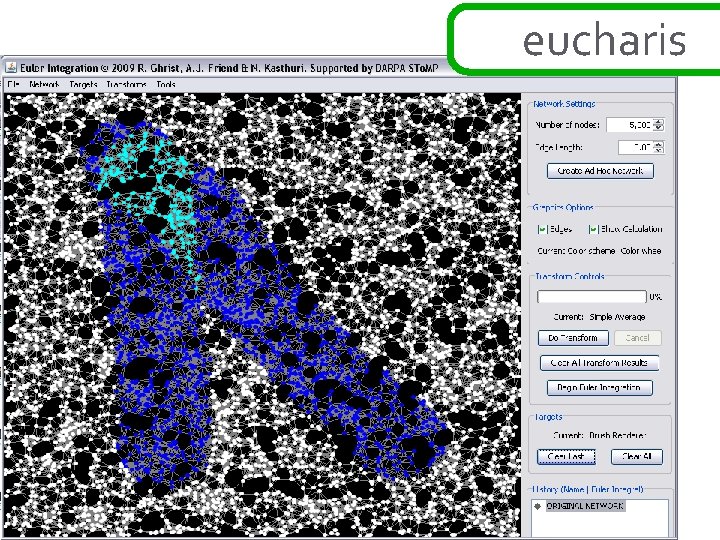
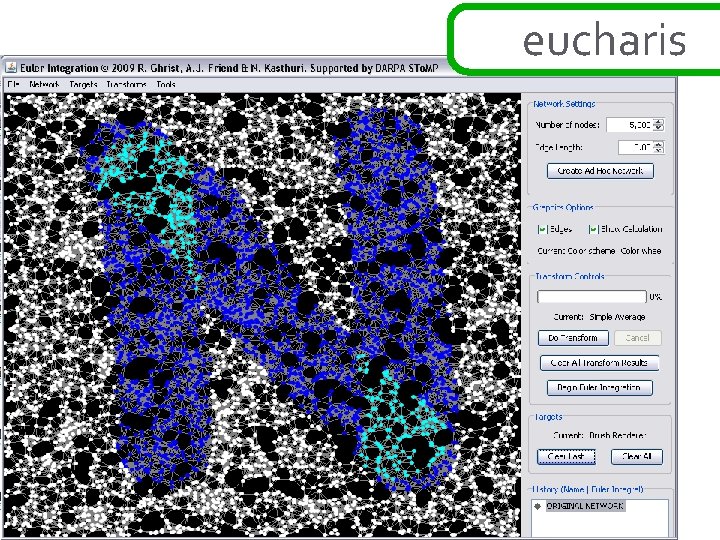
![ad hoc networks theorem: [BG] if the function h: R 2→N is sampled over ad hoc networks theorem: [BG] if the function h: R 2→N is sampled over](http://slidetodoc.com/presentation_image_h2/e010c2f15ff98d69c116c37e2bdb864c/image-22.jpg)
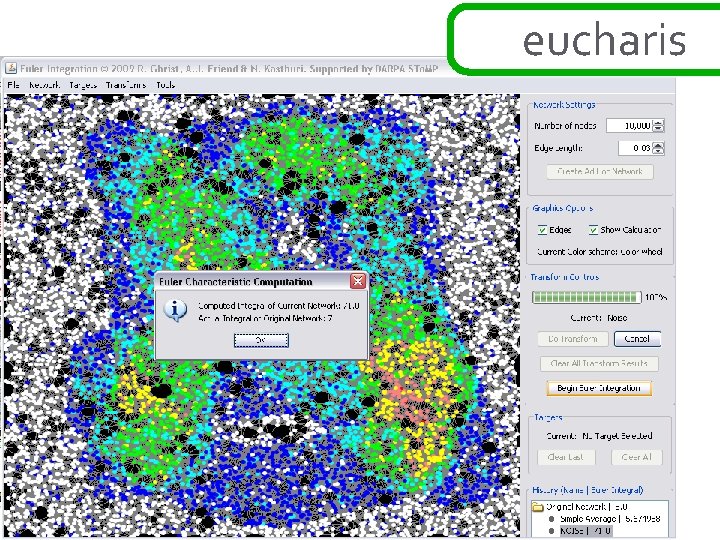
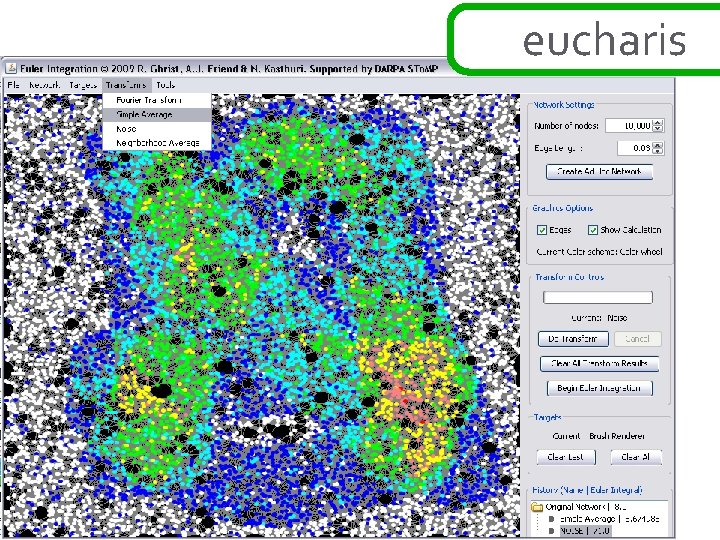
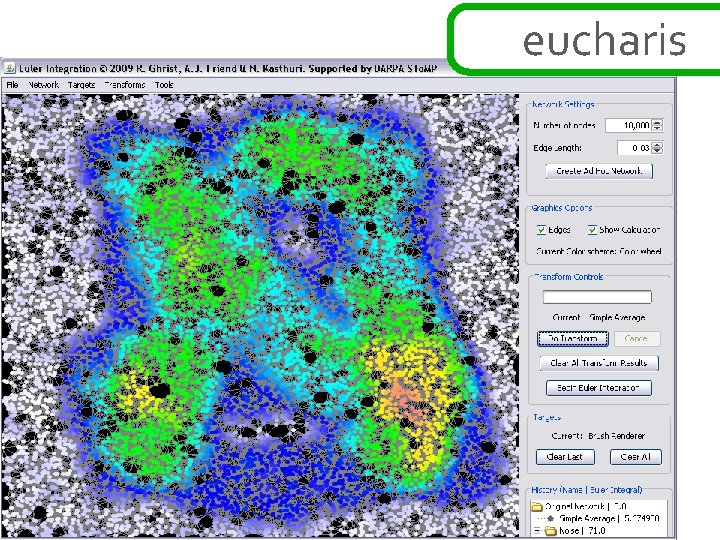
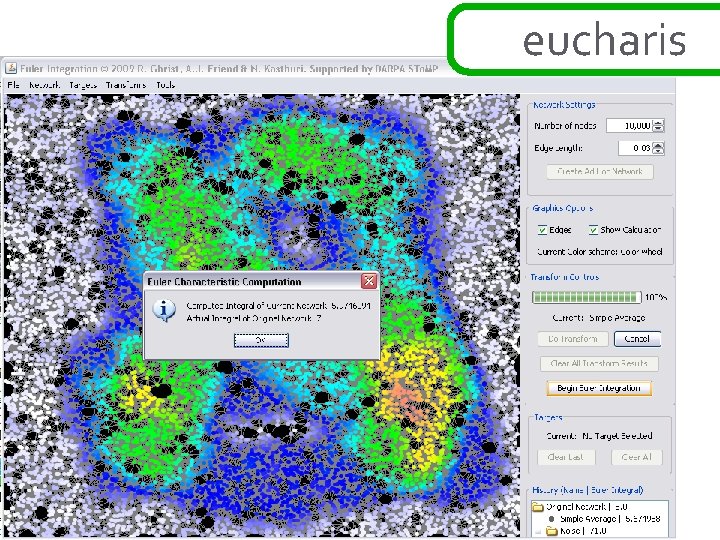
ad hoc networks theorem: [BG] if the function h: R 2→N is sampled over a network in a way that correctly samples the connectivity of upper and lower excursion sets, then the exact value of the euler integral ∞of h is Σ( #comp{ h≥s } - #comp{ h<s } + 1) s=1 this is a simple application of alexander duality… ∞ ∞ χ{ h ≥ s } = Σ ∫ h dχ = Σ s=1 ∞ s=1 b 0 {h ≥ s } – b 1{h ≥ s } ~ =Σ b 0{h ≥ s } – b 0{h < s } s=1 χ = Σ (-1)k dim H ∞ =Σ s=1 bk b 0{h ≥ s } – b 0{h < s } + 1 this works in ad hoc setting : clustering gives fast computation k
eucharis
eucharis
eucharis
eucharis
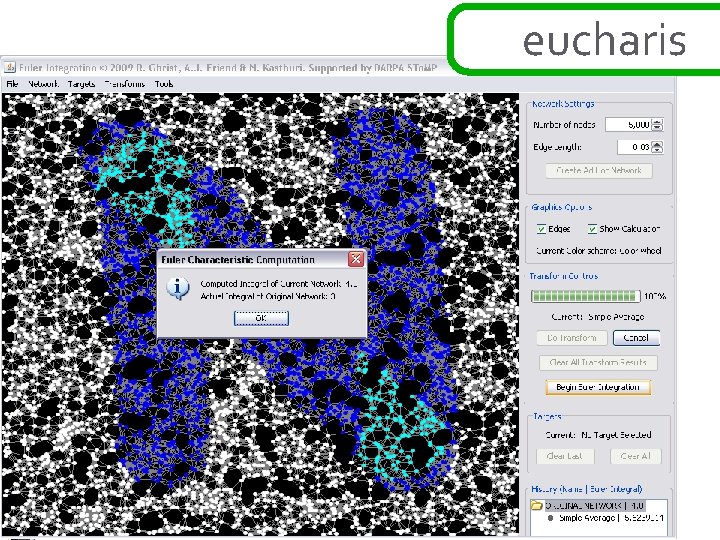
eucharis
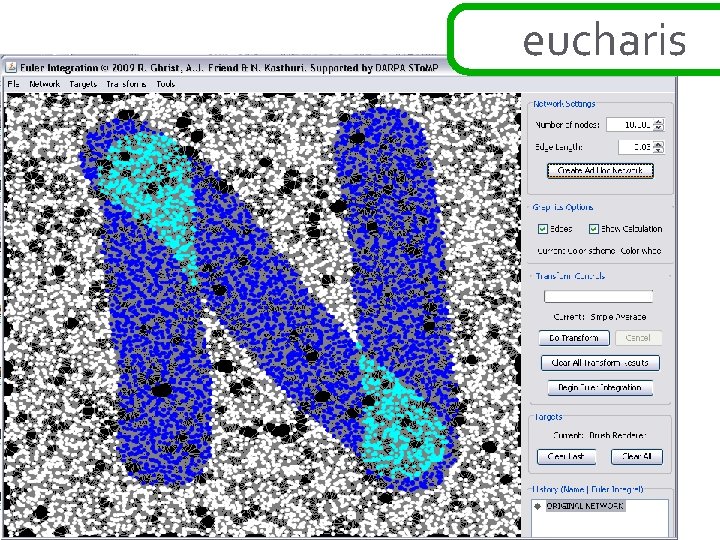
eucharis
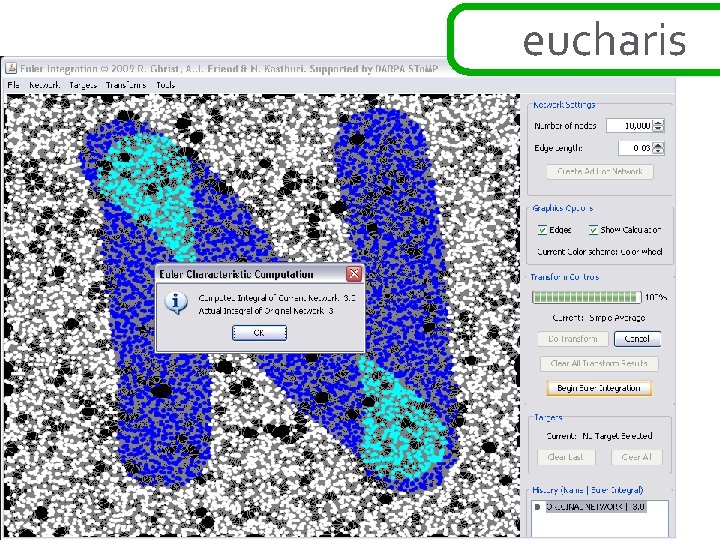
eucharis

get real…
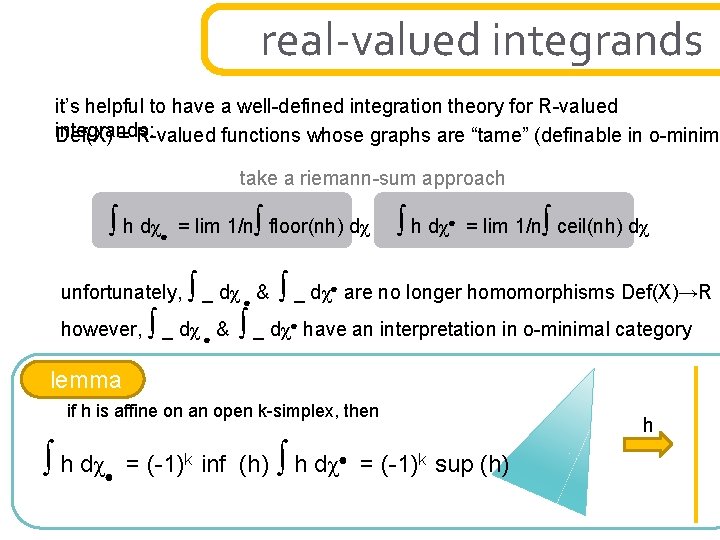
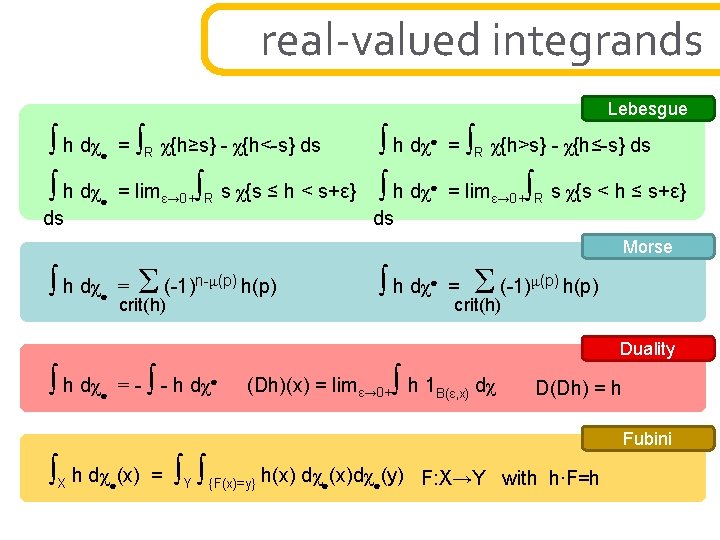
real-valued integrands it’s helpful to have a well-defined integration theory for R-valued integrands: Def(X) = R-valued functions whose graphs are “tame” (definable in o-minim take a riemann-sum approach ∫ h dχ● ∫ = lim 1/n floor(nh) dχ ∫ unfortunately, _ dχ ● & ∫ however, _ dχ ● & ∫ h dχ● ∫ = lim 1/n ceil(nh) dχ ∫ _ dχ● are no longer homomorphisms Def(X)→R ∫ _ dχ● have an interpretation in o-minimal category lemma if h is affine on an open k-simplex, then ∫ h dχ● = (-1)k inf (h) ∫ h dχ● = (-1)k sup (h) h

real-valued integrands intuition: the two measures correspond to the stratified morse in the graph of h in Def(X) with respect to two graph axis directions I*, I* : Def(X)→CF(X) theorem: [BG] for h in Def(X) ∫ h dχ∙ = ∫ h I*h dχ corollary: [BG] if h : X → R is morse on an n-manifold, then ∫ h dχ∙= Σ (-1)n-μ(p) h(p) ∫ h dχ∙= Σ (-1)μ(p) h(p) crit(h) μ = morse index ∫ h dχ∙ = ∫ h I*h dχ corollary: [BG] if h is univariate, then ∫ h dχ = totvar(h)/2 = - ∫ h ∙
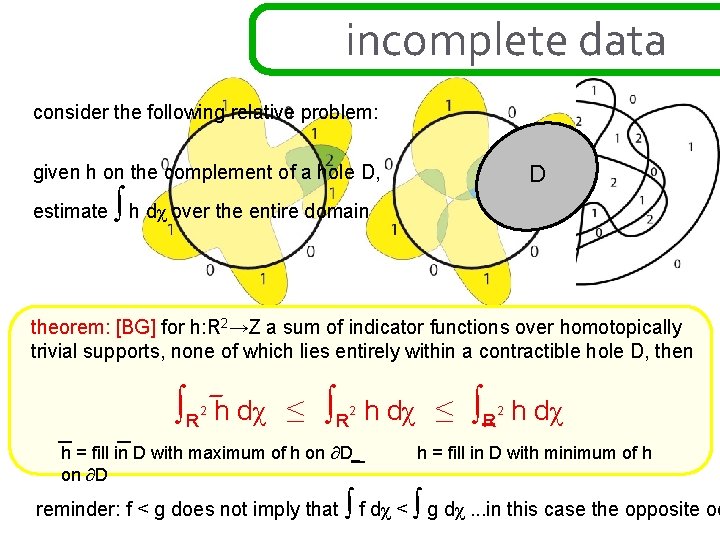
incomplete data consider the following relative problem: D given h on the complement of a hole D, estimate ∫ h dχ over the entire domain theorem: [BG] for h: R 2→Z a sum of indicator functions over homotopically trivial supports, none of which lies entirely within a contractible hole D, then ∫R 2 h dχ ≤ ∫R 2 h = fill in D with maximum of h on ∂D reminder: f < g does not imply that h dχ ≤ ∫R 2 h dχ h = fill in D with minimum of h ∫ f dχ < ∫ g dχ. . . in this case the opposite oc

incomplete data but what to choose in between upper and lower bounds? claim: a harmonic extension over a hole is a “best guess”. . . theorem: [BG] For h: R 2→Z a sum of indicator functions over homotopically trivial supports, none of which lies entirely within a contractible hole D, then ∫R 2 h dχ ≤ ∫R 2 f dχ ≤ ∫R 2 h dχ for f any “harmonic” extension of h over D (weighted average of h rel ∂D) the proof is surprisingly easy using morse theory: a “harmonic” extension has no local maxima or minima within D. . . # saddles in D - # maxima on ∂D = χ(D)=1 the integral over D is the heights of the maxima minus the heights of the saddles
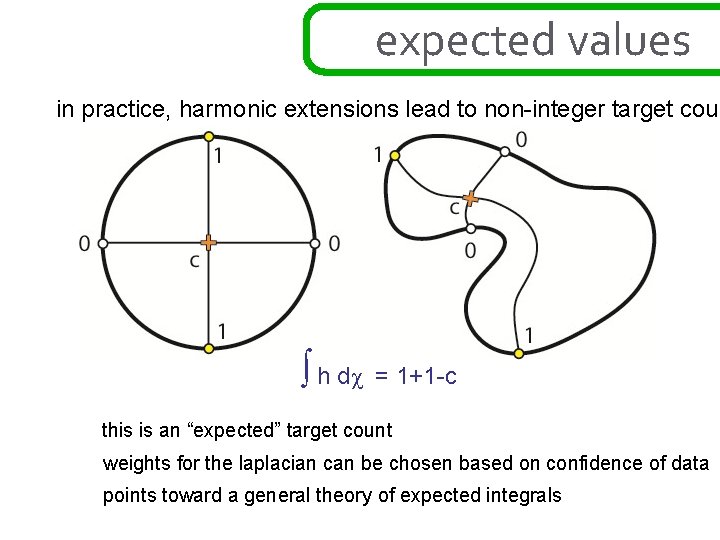
expected values in practice, harmonic extensions lead to non-integer target coun ∫ h dχ = 1+1 -c this is an “expected” target count weights for the laplacian can be chosen based on confidence of data points toward a general theory of expected integrals

integral transforms
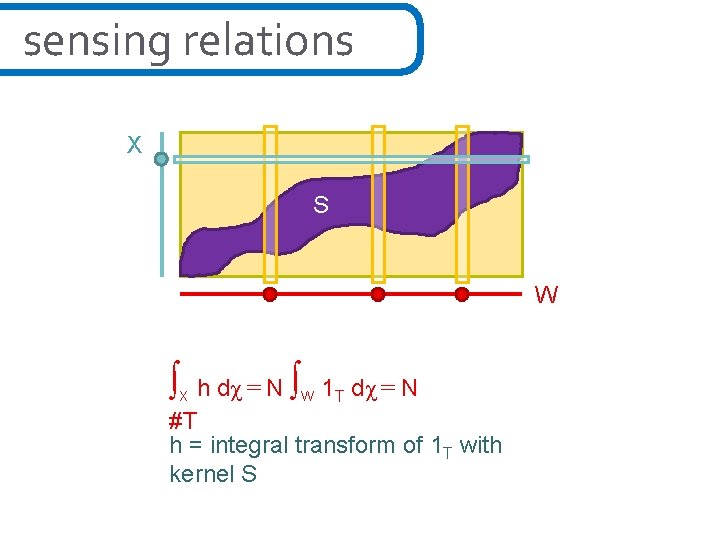
sensing relations X S W ∫ ∫ h dχ = N W 1 T dχ = N #T h = integral transform of 1 T with kernel S X

fourier transform
radon transform

bessel transform
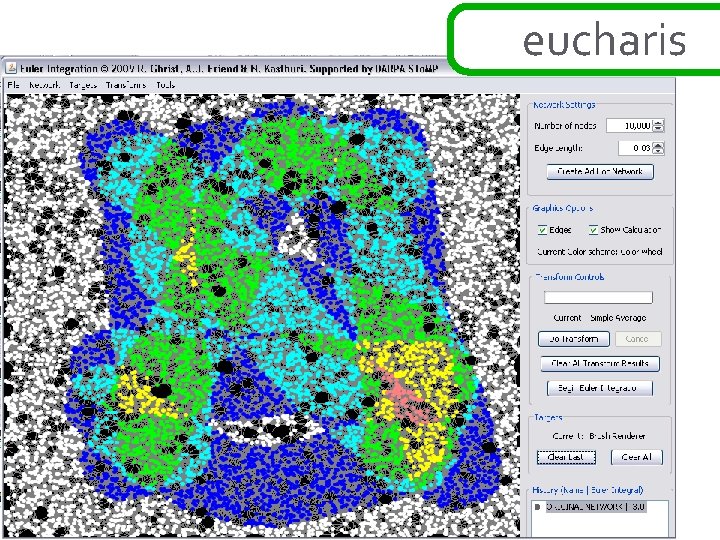
eucharis
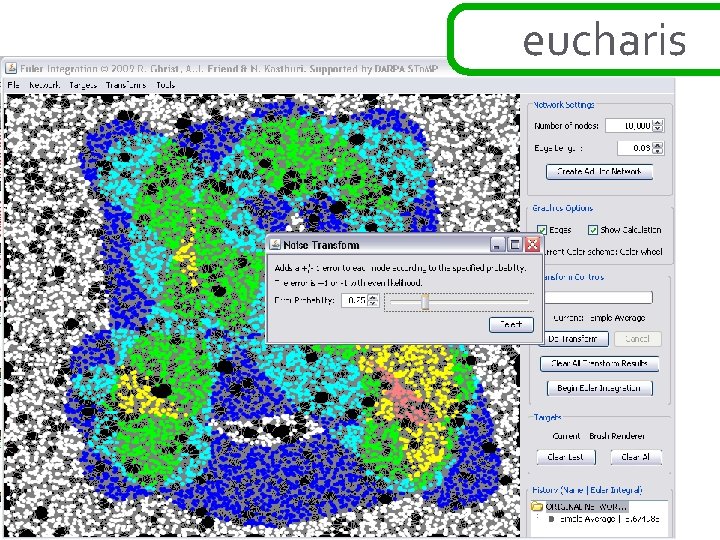
eucharis
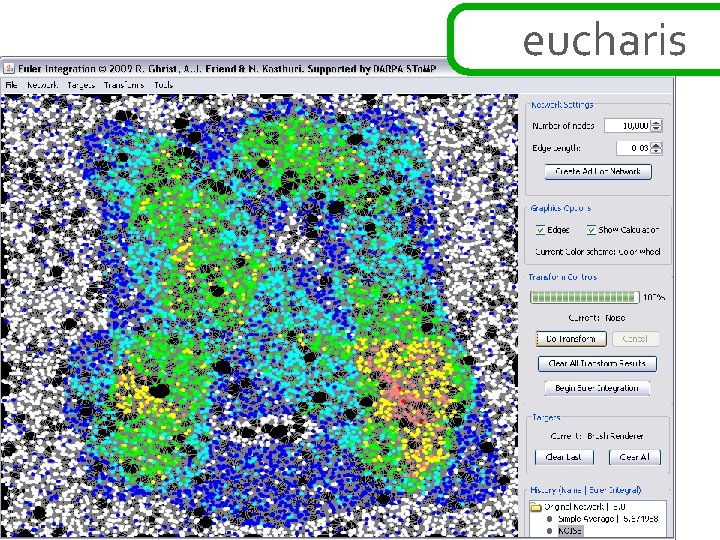
eucharis
eucharis
eucharis
eucharis
eucharis
open questions how to correct “side lobes” and energy loss in integral transforms? what is the appropriate integration theory for multi-modal and logical-valued data? how to efficiently compute integral transforms given discrete (sparse) data? …and, well, numerical analysis in general
topological network topology

closing credits… research sponsored by darpa (stomp program) national science foundation office of naval research primary collaborator yuliy baryshnikov, bell labs work in progress with professional support java code michael robinson, penn matthew wright, penn university of pennsylvania a. mitchell david lipsky, uillinois, urbana a. j. friend, stanford naveen kasthuri, penn
- Slides: 51