EULER BENDING VIBRATION mode 1 Hugh Hunt Trinity

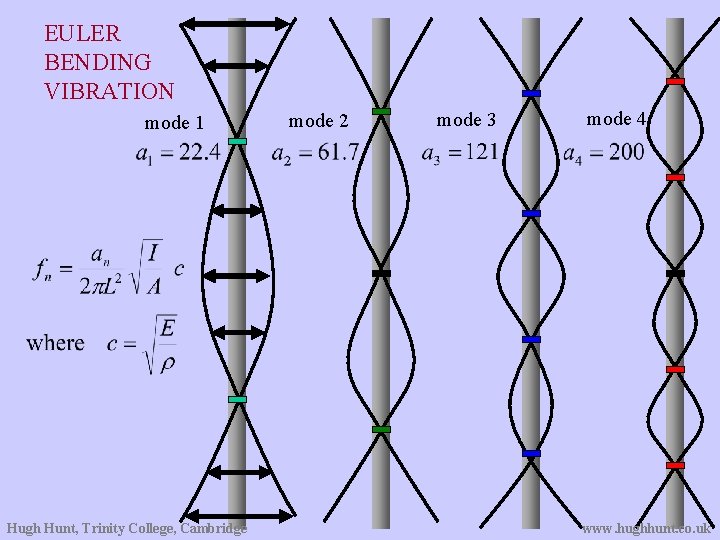
EULER BENDING VIBRATION mode 1 Hugh Hunt, Trinity College, Cambridge mode 2 mode 3 mode 4 www. hughhunt. co. uk

Free vibration of a beam y z mass per unit length m flexural rigidity EI, length L Equation of motion: For vibration, assume y(x, t)=Y(x)cos(wt), so This has general solution Boundary condition for a fee end at z=0: Hugh Hunt, Trinity College, Cambridge www. hughhunt. co. uk

so i. e. C=A and D=B Boundary condition for a free end at z=L: so and or, in matrix form, Hugh Hunt, Trinity College, Cambridge www. hughhunt. co. uk

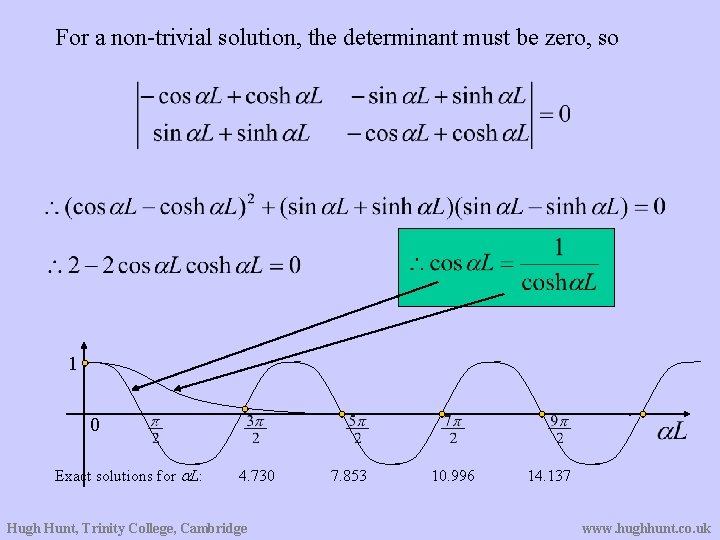
For a non-trivial solution, the determinant must be zero, so 1 0 Exact solutions for a. L: 4. 730 Hugh Hunt, Trinity College, Cambridge 7. 853 10. 996 14. 137 www. hughhunt. co. uk

From a. L the frequencies of free vibration are found using aj= 22. 37, 61. 67, 120. 90, 199. 86, . . . or aj The corresponding mode shapes are obtained by substituting aj into the matrix equation to find the ratio between A and B so that The location of nodal points is then found by looking for where Y(z)=0 Hugh Hunt, Trinity College, Cambridge www. hughhunt. co. uk

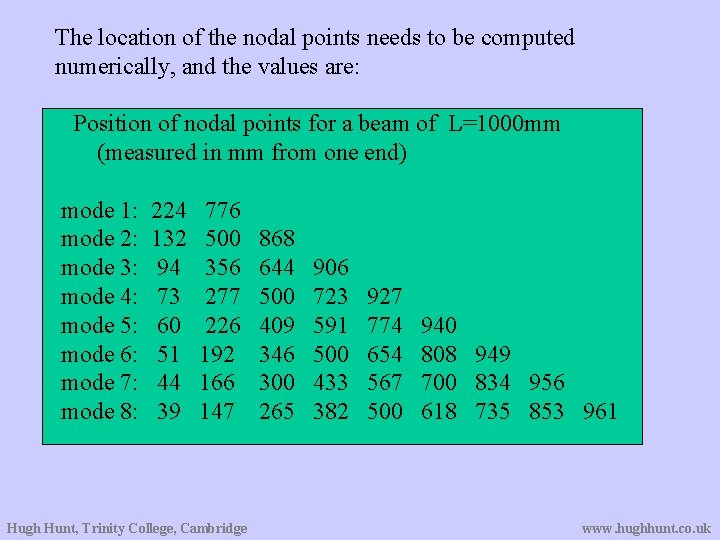
The location of the nodal points needs to be computed numerically, and the values are: Position of nodal points for a beam of L=1000 mm (measured in mm from one end) mode 1: mode 2: mode 3: mode 4: mode 5: mode 6: mode 7: mode 8: 224 132 94 73 60 51 44 39 776 500 356 277 226 192 166 147 Hugh Hunt, Trinity College, Cambridge 868 644 500 409 346 300 265 906 723 591 500 433 382 927 774 654 567 500 940 808 949 700 834 956 618 735 853 961 www. hughhunt. co. uk