ETERNAL DOMINATION Chip Klostermeyer 6 vertices 7 edges

ETERNAL DOMINATION Chip Klostermeyer

6 vertices 7 edges Dominating Set γ=2 Graph

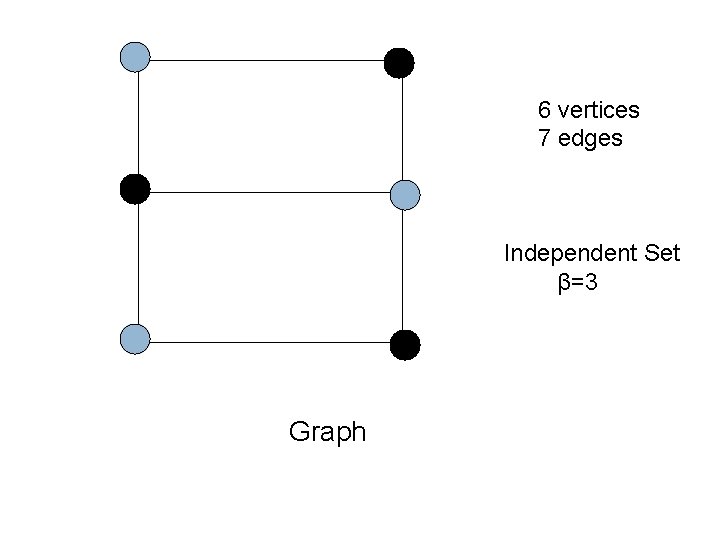
6 vertices 7 edges Independent Set β=3 Graph

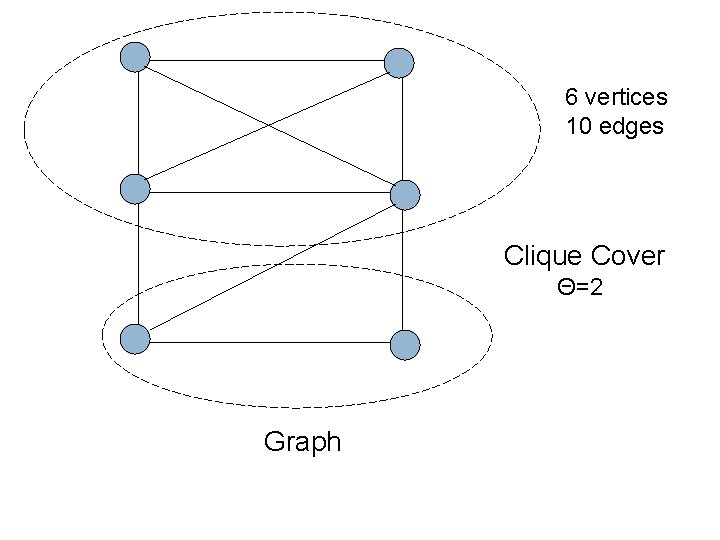
6 vertices 10 edges Clique Cover Θ=2 Graph

Eternal Dominating Set • • • Defend graph against sequence of attacks at vertices At most one guard per vertex Send guard to attacked vertex Guards must induce dominating set One guard moves at a time (later, we allow all guards to move)

2 -player game • • Attacker chooses vertex with no guard to attack Defender chooses guard to send to attacked vertex (must be sent from neighboring vertex) Attacker wins if after some # of attacks, guards do not induce dominating set Defender wins otherwise

Eternal Dominating Set γ∞=3 γ γ=2 Attacked Vertex in red Guards on black vertices

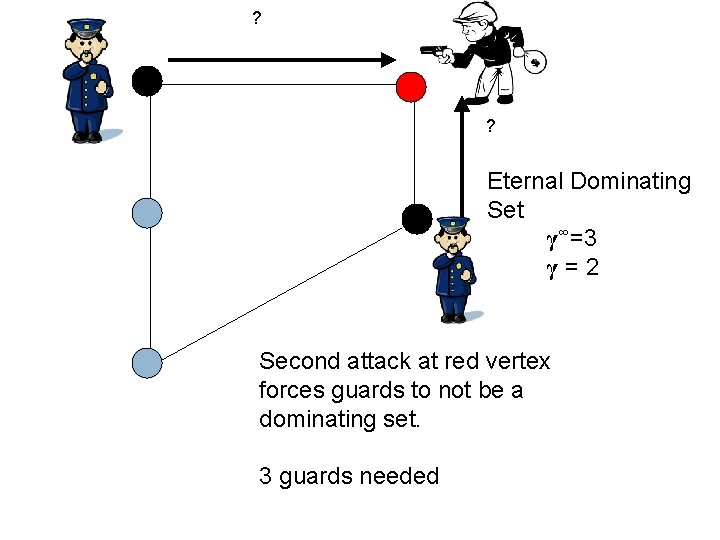
? ? Eternal Dominating Set γ∞=3 γ=2 Second attack at red vertex forces guards to not be a dominating set. 3 guards needed

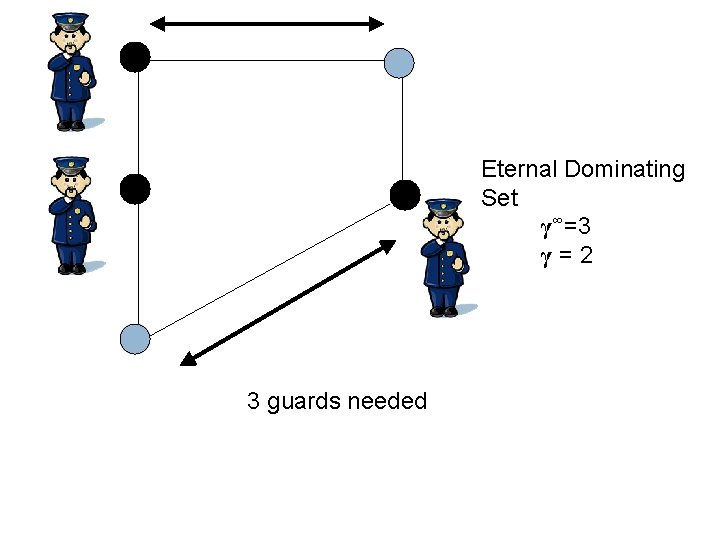
Eternal Dominating Set γ∞=3 γ=2 3 guards needed

Basic Bounds γ ≤ β ≤ γ∞ ≤ Θ Because one guard can defend a clique and attacks on an independent set of size k require k different guards

Problem Goddard, Hedetniemi asked if γ∞ ≤ c * β and they showed graphs for which γ∞ < Θ Smallest known has 11 vertices. Question: Is there a smaller one?

Upper Bound Klostermeyer and Mac. Gillivray proved γ∞ ≤ C(β+1, 2) C(n, 2) denotes binomial coefficient Proof is algorithmic.

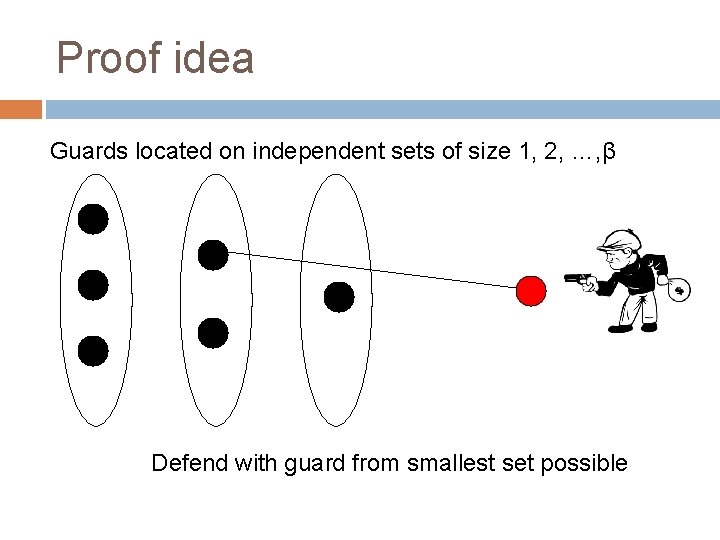
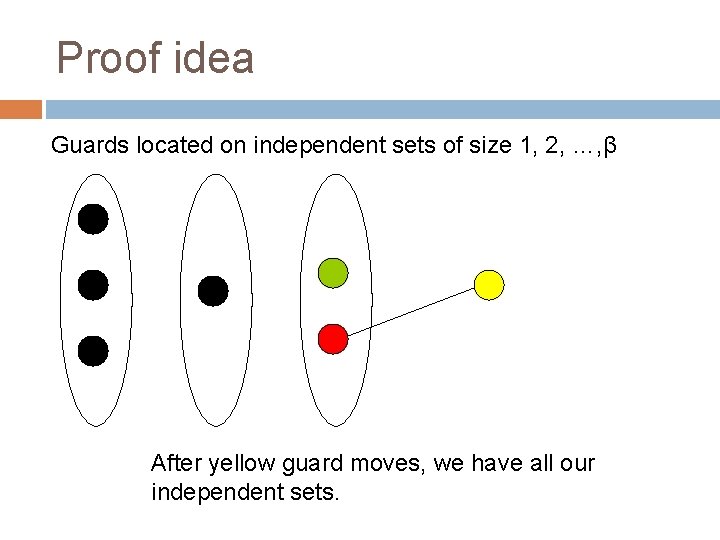
Proof idea Guards located on independent sets of size 1, 2, …, β Defend with guard from smallest set possible

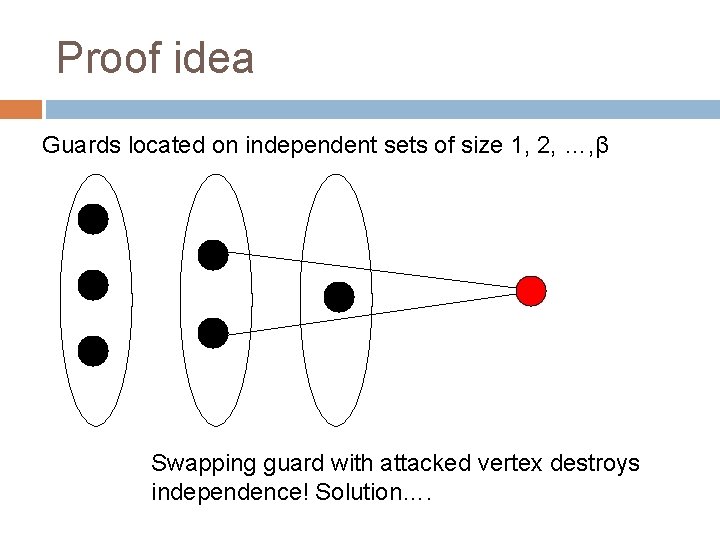
Proof idea Guards located on independent sets of size 1, 2, …, β Swapping guard with attacked vertex destroys independence! Solution….

Proof idea Guards located on independent sets of size 1, 2, …, β Choose union of independent sets to be LARGE as possible

Proof idea Guards located on independent sets of size 1, 2, …, β After yellow guard moves, we have all our independent sets.

Lower Bound Upper bound: γ∞ ≤ C(β+1, 2) Certain large complements of Kneser graphs require this many guards. Problem: find small circulants where bound is tight. C 22[1, 2, 4, 5, 9, 11]

γ ≤ β ≤ γ∞ ≤ Θ γ∞ =Θ for Perfect graphs [follows from PGT] Series-parallel graphs [Anderson et al. ] Powers of Cycles and their complements [KM] Circular-arc graphs [Regan] Open problem: planar graphs

Open Questions Is there a graph G with γ = γ∞ < Θ ? No triangle-free; none with maximum-degree three. Planar? Is there a triangle-free graph G with β = γ∞ < Θ ? Is γ∞(G x H) ≥ γ∞ (G) γ∞ (H)?

The Fundamental Conjecture For any vertex v in any minimum eternal dominating set D there is a vertex u adjacent to v such that D–v+u is an eternal dominating set.

Fundamental Theorem Given any graph G and minimum eternal dominating set D containing v, there is a minimum eternal dominating set D’ not containing v. Corollary: For all graphs G γ∞(G-v) ≤ γ∞(G)

M-Eternal Dominating Set γ∞m=2 All guards can move in response to attack

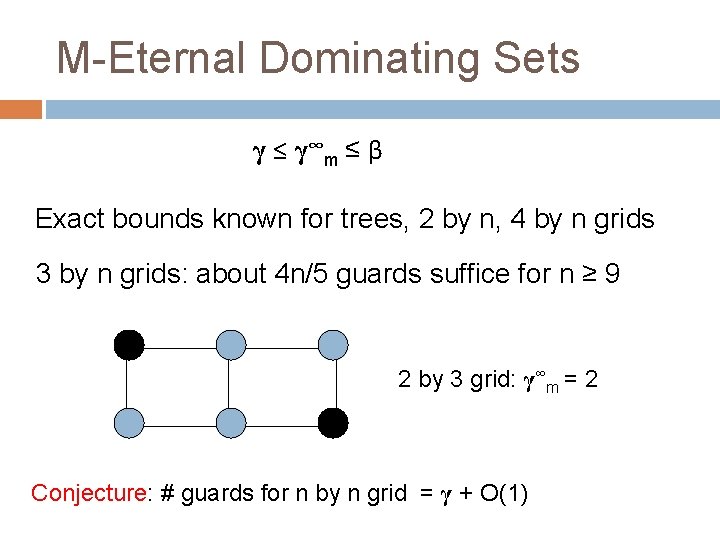
M-Eternal Dominating Sets γ ≤ γ ∞m ≤ β Exact bounds known for trees, 2 by n, 4 by n grids 3 by n grids: about 4 n/5 guards suffice for n ≥ 9 2 by 3 grid: γ∞m = 2 Conjecture: # guards for n by n grid = γ + O(1)

M-Eternal Dominating Sets Known that γ∞m ≤ n/2; sharp for odd length paths, many trees What about graphs with minimum degree 3? Petersen graph is 2 n/5; we know no other examples with more than 3 n/8 (and no large cubic ones with 3 n/8) Cubic Bipartite graphs: γ∞m ≤ 7 n/16 [HKM] • Improve upper bound for minimum degree three • Find infinite families needing close to 2 n/5 guards.

Proof idea Cubic Bipartite graphs: γ∞m ≤ 7 n/16 Remove perfect matching M. Cycles remain: Long cycles adjacent to no 4 -cycle (via M) n/3 guards Long cycles connected to 4 -cycles (via M) 7 n/16 guards (8 -cycles are obstacle) 4 -cycles connected to each other (via M) 3 n/7 guards

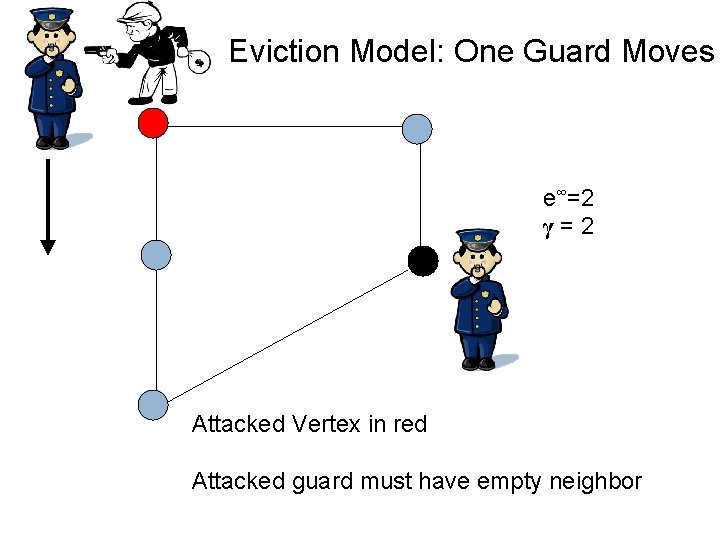
Eviction Model: One Guard Moves e∞=2 γ=2 Attacked Vertex in red Attacked guard must have empty neighbor

Eviction: One guard moves • e∞ ≤ Θ • e∞ ≤ β for bipartite graphs • e∞ > β for some graphs • e∞ ≤ β when β=2 • e∞ ≤ 5 when β = 3 • Question: Find graphs with β = 3 and e∞ = 5 • Question: Is e∞ ≤ γ∞ for all G?

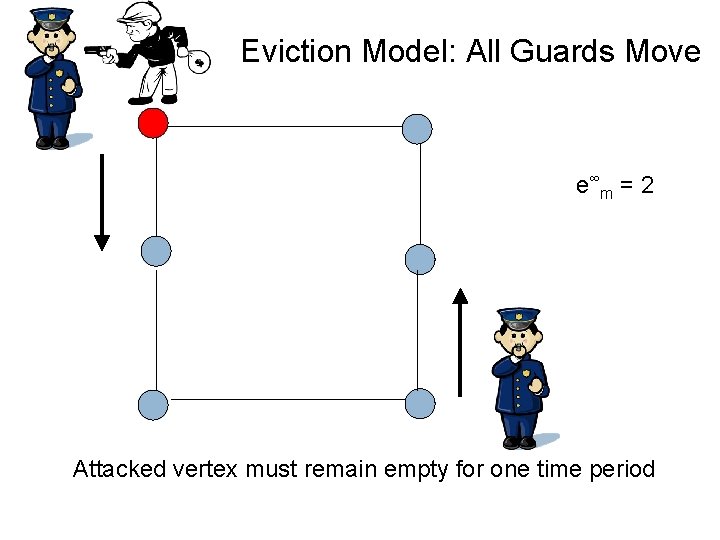
Eviction Model: All Guards Move e∞ m = 2 Attacked vertex must remain empty for one time period

Eviction: All guards move • e m∞ ≤ β • Grids: m by n solved for m ≤ 4 Bound: em∞ ≤ (n+2)(m+3)/5 – 4 for m, n ≥ 8 • Question: Is em∞ ≤ γ∞m for all G? (swap model only, else star is counterexample)

Mixed Model Combine eternal domination and eviction: Attack at vertex w/o guard: guard moves there Attack at vertex w/ guard : guard moves away • Denote by m∞ • Question: Is m∞ ≤ 6 when β = 3? • Question: Is m∞ = γ∞ for all G?

Eternal Independent Sets • One model defined by Hartnell and Mynhardt • Caro & Klostermeyer define alternate model: • • Maintain an independent set of guards eternally Attacks are at vertices with guards (like eviction) Maximize # of guards One guard moves or all-guards move or ALL guards move

Eternal Independent Sets • Questions • Find graphs where eternal independence # (all guards move) equals size of maximum matching. It is true for bipartite graphs. • Find graphs where eternal independence # (all guards move) equals the independence number • Characterize graphs where eternal independence # (one guard moves) equals size of maximum induced matching (a lower bound for eternal independence #)

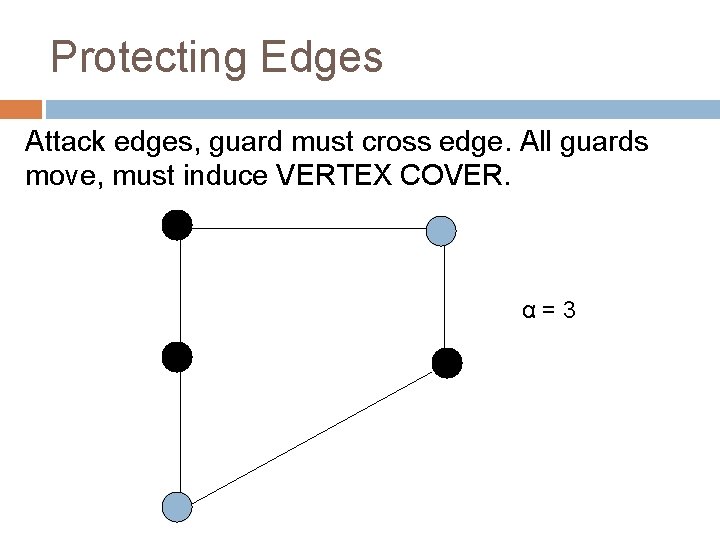
Protecting Edges Attack edges, guard must cross edge. All guards move, must induce VERTEX COVER. α=3

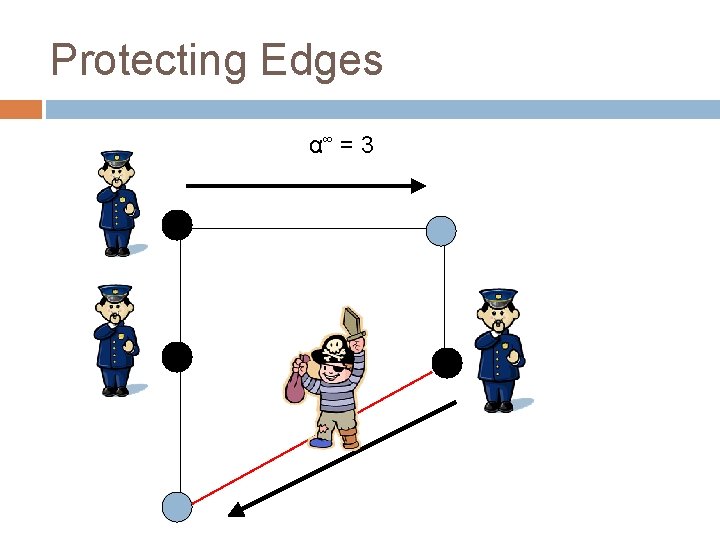
Protecting Edges α∞ = 3

Edge Protection • • § § § Theorem: α ≤ α∞ ≤ 2α Which graphs have α = α∞? Grids Kn X G Circulants, others. Is it true for vertex-transitive graphs? Is it true for G X H if it is true for G and/or H?

More Edge Protection • • • Which graphs have α∞ = γ∞m ? Trees with property characterized. No bipartite graph with δ ≥ 2 except C 4 No graph with δ ≥ 2 except C 4 Which graphs with pendant vertices?

Vertex Cover • • • m-eternal domination number is less than eternal vertex cover number for all graphs of minimum degree 2, except for C 4. m-eternal domination number is less than vertex cover number for all graphs of minimum degree 2 and girth 7 and ≥ 9. What about girths 5, 6, 8?