Estudio y representacin de funciones Matemticas I Macarena

Estudio y representación de funciones Matemáticas I Macarena González Lobo Antonio Izquierdo Laynez Cristina Sosa Orta

Introducción histórica Descartes y Fermat estudiaron en profundidad las curvas y sus ecuaciones, pero las habían tratado como casos individualizados. A partir de ellos, muchos matemáticos a lo largo del siglo XVII se esforzaron en el estudio de las curvas, pero ninguno dio con los elementos que permitían establecer un método general. Newton y Leibniz lo proporcionaron, e introdujeron un tipo de técnicas que permitían estudiar con las mismas herramientas los problemas de física y geometría. Sus avances en el cálculo diferencial e integral posibilitaron un desarrollo de las matemáticas espectacular, cuyo resultado se apreció posteriormente durante los siglos XVIII y XIX. Desde el punto de vista del desarrollo de las matemáticas, les corresponde a estos dos autores la elaboración de un método general y nuevo, que puede aplicarse a muchos tipos de problemas sobre el cálculo algebraico, el infinitesimal y, en general, a toda la geometría analítica. El concepto de función se hizo el eje central de la matemática, sobre todo en el análisis. Su estudio se hizo totalmente indispensable para llevar adelante el desarrollo científico y tecnológico. El nombre de “función” proviene del gran matemático Leibniz, y su estudio más profundo sobre funciones fue estimulado por su interés geométrico de analizar, matemáticamente, los puntos de las curvas donde éstas alcanzan su máximo y su mínimo valor y dar un método general para determinar las rectas tangentes es estos puntos. Estos cálculos se realizan mediante el cálculo de las funciones derivadas y forman parte importante del cálculo diferencial, que se estudia más adelante.

Introducción histórica Newton y Leibniz, los dos grandes científicos de finales del siglo XVII y principios del XVIII, vivieron en una Europa caracterizada por la revolución del realismo científico y la explosión cultural del Barroco. Newton, en su obra ”Methodus fluxionum et serierum infiniturum”, introduce su nueva concepción de fluxiones y fluentes al abordar dos problemas; el primero consiste en encontrar la velocidad del movimiento en un tiempo dado cualquiera, dada la longitud del espacio descrito. El segundo problema es la inversa del primero. Disponiendo de su método general, determina los máximos y mínimos de relaciones, las tangentes a curvas, el radio de curvatura, los puntos de inflexión y el cambio de concavidad de las curvas, su área y su longitud. Isaac Newton (1642 -1727) Gottfried Leibniz (1646 -1716)

Justificación ¢ ¢ ¢ ¢ Contexto: Esta unidad se enmarca en el bloque IV (Análisis) de 1º de Bachillerato. Las funciones nacen de la necesidad de resolver problemas prácticos y se sustentan por su capacidad para tratar, explicar, predecir y modelar situaciones reales y dar rigor a los conocimientos científicos. Tienen una fuerte conexión con la realidad, debido a su constante interrelación con otras áreas, especialmente en el ámbito de la ciencia y la técnica. El estudio de las funciones es principalmente estratégico y se manifiesta en tres aspectos: como base conceptual, como instrumento esencial de desarrollo de la Ciencia y la Tecnología y como valor inherente a la propia cultura. El alumnado debe aprender a apreciar la utilidad de las funciones, sobre todo, su capacidad para dar respuesta a la mayoría de las necesidades humanas. Los contenidos de esta lección proporcionan técnicas básicas, tanto para estudios posteriores como para la actividad profesional. No se trata de que los estudiantes posean muchas herramientas matemáticas, sino que las manejen con destreza y oportunidad. Las herramientas tecnológicas, en particular el uso de calculadoras y aplicaciones informáticas, pueden servir de ayuda tanto para la mejor comprensión de conceptos y la resolución de problemas complejos como para el procesamiento de cálculos. Esta unidad será la base para poder adquirir los conceptos que se estudiarán en lecciones posteriores. Además, contribuye mejorando la adquisición de cualidades como la constancia, la autonomía, la adquisición de nuevos saberes y habilidades y la curiosidad por la investigación.

Objetivos ¢ ¢ ¢ Calcular dominios y recorridos de funciones reales de variable real. Distinguir correspondencias funcionales de las que no lo son. Representar gráficamente funciones polinómicas, racionales, radicales, exponenciales, logarítmicas, trigonométricas y algunas transformaciones de dichas funciones. Saber y saber aplicar los conceptos de función par/impar, así como las simetrías correspondientes de sus gráficas. Saber qué es una función creciente/decreciente, monótona en un intervalo y saber aplicar esos conceptos al análisis de funciones elementales. Saber qué son funciones periódicas y distinguir su periodo gráficamente.

Contenidos ¢ Conceptuales: l l l l Concepto de función. Dominio e imagen de una función. Gráficas de funciones polinómicas, racionales, radicales, exponenciales, logarítmicas, trigonométricas y algunas transformaciones de dichas funciones. Simetrías. Crecimiento y decrecimiento. Máximos y mínimos. Funciones periódicas. Asíntotas.

Contenidos ¢ Procedimentales: l l l l Expresión en forma funcional de reglas y relaciones descritas en lenguaje convencional. Cálculo de dominios y recorridos de funciones. Distinción entre correspondencias que son funciones y las que no lo son. Trazado de gráficas de funciones. Uso de la calculadora para hacer tablas de valores. Análisis de la paridad de funciones y de la simetría de sus gráficas. Cálculo de máximos y de mínimos funcionales. Análisis y representación de funciones periódicas.

Contenidos ¢ Actitudinales: l l l Valoración de la potencia del cálculo de funciones en la resolución de problemas de la vida real. Reconocimiento del papel de las funciones en el estudio de los cambios de un proceso natural, social o técnico de la realidad. Receptividad, curiosidad e interés por el planteamiento, la investigación y la resolución de problemas, mediante las características analíticas de las funciones que describen los fenómenos que estudian. Gusto por la interpretación de problemas de aplicación a casos reales. Gusto por la limpieza y claridad.

Organización de las sesiones ¢ SESIÓN 1: l l ¢ Prueba inicial. Motivación. SESIÓN 2: l l l Definición de función, dominio y recorrido. Ejercicio en clase. Características del comportamiento de las funciones: raíces, monotonía, máximos y mínimos, continuidad, funciones escalonadas, simetrías (par/impar), periodicidad, asíntotas. Funciones polinómicas. Ejemplo. Ejercicios en clase y para casa. Realización de dichos ejercicios en Geogebra.

Organización de las sesiones ¢ SESIÓN 3: l l l ¢ Corrección ejercicios de casa. Funciones racionales. Ejemplo. Ejercicio en clase y para casa de investigación. Funciones radicales. Ejemplo. Ejercicio en clase y para casa. Realización de dichos ejercicios en Geogebra. SESIÓN 4: l l Corrección ejercicios de casa. Funciones a trozos. Ejemplo. Ejercicios en clase y para casa. Realización de dichos ejercicios en Geogebra.

Organización de las sesiones ¢ SESIÓN 5: l l ¢ Corrección ejercicios de casa. Algunas transformaciones de funciones. l Simetrías. l Valor absoluto. l Traslaciones. l Dilataciones o contracciones. Ejercicio en clase y para casa. Realización de dichos ejercicios en Geogebra. SESIÓN 6: l l l Corrección ejercicios de casa. Funciones exponenciales. Ejercicios en clase y para casa. Funciones logarítmicas. Ejercicios en clase y para casa. Realización de dichos ejercicios en Geogebra.

Organización de las sesiones ¢ SESIÓN 7: l l ¢ Corrección ejercicios de casa. Funciones trigonométricas. l Transformaciones de las funciones trigonométricas. Ejercicios en clase y para casa. Sesión Geo. Gebra. SESIÓN 8: l l l Corrección ejercicios de casa. Ejercicios en clase de repaso. Resolución de dudas previas al examen.

Organización de las sesiones ¢ SESIÓN 9: l ¢ Examen. SESIÓN 10: l l l Revisión del examen. Ejercicios de refuerzo para el examen de recuperación. Ejercicios de ampliación para quien quiera subir nota.

Prueba inicial I 1. Un empresario paga mensualmente a cada empleado 720 € por un determinado trabajo. Además le abona 6 € por cada unidad que produce el empleado durante ese mes. a) Define la función I(n) que da los ingresos de un empleado en función de las unidades producidas n. b) Escribe y representa gráficamente las parejas (n, I(n)), unidades producidas e ingresos correspondientes, en los casos de producir 5, 10 y 15 unidades. c) ¿Para qué valores de n tiene sentido considerar el valor I (n) en el contexto del enunciado?

Prueba inicial I 2. Un rectángulo tiene 20 cm de perímetro. Encuentra una expresión para el valor del área, A, del rectángulo, en función de la base, x, de dicho rectángulo. a) ¿Cuáles son los valores posibles de la longitud de la base? b) Representa gráficamente la función obtenida para los valores posibles de x. c) A la vista de la gráfica, describe el crecimiento o decrecimiento del valor del área cuando crece la longitud de la base. ¿Para qué valor de ésta se alcanza el mayor área?

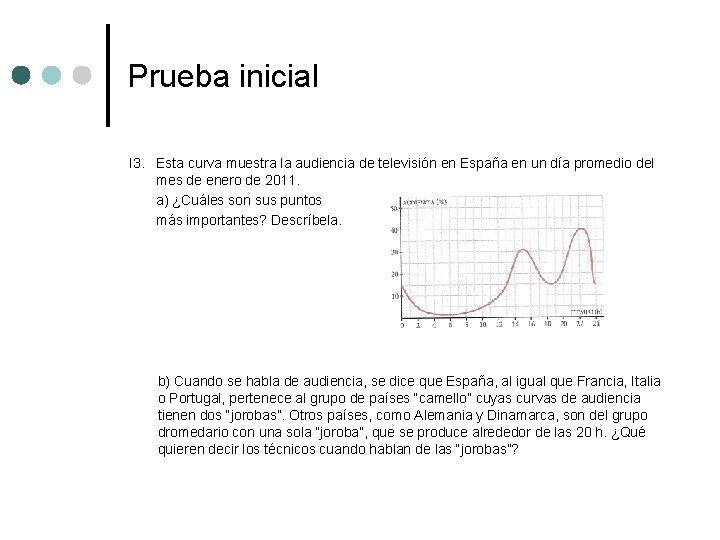
Prueba inicial I 3. Esta curva muestra la audiencia de televisión en España en un día promedio del mes de enero de 2011. a) ¿Cuáles son sus puntos más importantes? Descríbela. b) Cuando se habla de audiencia, se dice que España, al igual que Francia, Italia o Portugal, pertenece al grupo de países “camello” cuyas curvas de audiencia tienen dos “jorobas”. Otros países, como Alemania y Dinamarca, son del grupo dromedario con una sola “joroba”, que se produce alrededor de las 20 h. ¿Qué quieren decir los técnicos cuando hablan de las “jorobas”?

Objetivos de la Prueba inicial ¢ Problema 1 l ¢ El objetivo de esta tarea es que los alumnos pasen un problema contextualizado al modo algebraico. Después han de transformarlo a una tabla de valores que han de transformar al modo gráfico. Tienen que saber reconocer el dominio de la función tanto en general como para el contexto en el que se sitúa. Los objetivos al pedirles esta tarea del curso anterior son representación de funciones lineales a partir de un contexto, dominio de dichas funciones, contextualizar la función con el enunciado. Problema 2 l El objetivo de esta tarea es que los alumnos pasen un problema contextualizado al modo algebraico, el cual, también tendrán que contextualizar. Después han de transformarlo a una tabla de valores que han de transformar al modo gráfico. Después deben trabajar en ese modo para llevar la información que da este modo a una descripción verbal. Los objetivos al pedirles esta tarea del curso anterior son representación de funciones cuadráticas a partir de un contexto, dominio de dichas funciones, contextualizar la función con el enunciado. Estudio del crecimiento, decrecimiento y extremos a partir de la gráfica.

Objetivos de la Prueba inicial ¢ Problema 3 l El objetivo de esta tarea es que los alumnos conviertan un problema contextualizado y acompañado de una gráfica en una descripción verbal mediante la interpretación de la gráfica dada, es decir, que reconozcan y analicen las funciones que desempeñan los gráficos en la mejor comprensión de los mensajes. Dichos mensajes son interpretación de la información de una gráfica en un contexto, estudio del crecimiento, decrecimiento y máximos relativos a partir de la gráfica.

Motivación ¢ Actividad por parejas. Un componente de la pareja corre una vuelta alrededor de la pista de fútbol, y al llegar al punto inicial comienza a medirse las pulsaciones. El otro componente de la pareja anotará las pulsaciones a los: a) b) c) d) 15’’ 30’’ 45’’ 60’’ e) f) g) h) 1’ 30’’ 2’ 3’ 5’ Una vez obtenidos los datos anteriores, obtened la gráfica que representa el número de pulsaciones en función del tiempo transcurrido. ¿Puedes predecir cuántas pulsaciones tendrás si las contaras al cabo de 1 hora en reposo? Razona tu respuesta. ¿En qué momento de los representados tendrías más pulsaciones?

Desarrollo Definición, dominio y recorrido ¢ Definición de función: Una función f es una relación entre dos conjuntos A y B, de manera que a cada valor del primero, A le hace corresponder un único valor del segundo, B. f: A→B x→f(x) ¢ Dominio de la función: Es el conjunto de valores que puede tomar la variable independiente x. ¢ Recorrido: Es el conjunto de valores que toma la función.

Desarrollo Definición, dominio y recorrido EJERCICIOS PARA CLASE C 1. ¿Cuál de estas gráficas son funciones?

Desarrollo Características del comportamiento de las funciones ¢ Raíces. Puntos de corte con los ejes. l l ¢ El eje de abscisas es la recta de ecuación y=0. Para hallar los puntos de corte de una función y=f(x) con el eje de abscisas, basta resolver la ecuación f(x)=0. Estos puntos se denominan también raíces. El eje de ordenadas es la recta de ecuación x=0. El punto de corte de una función con el eje de ordenadas, si existe, es (0, f(0)), ya que cada x puede tener, a lo sumo, una imagen f(x), el corte con el eje OY es, a lo sumo, uno. Monotonía. l l f(x) es creciente en un punto x=a ↔ f(a-h)≤f(a+h) f(x) es creciente en un intervalo (X 1, X 2) cuando lo es para todo x entre X 1 y X 2. f(x) es decreciente en un punto x=a ↔ f(a-h)≥f(a) ≥f(a+h) f(x) es decreciente en un intervalo (X 1, X 2) cuando lo es para todo x de él.

Desarrollo Características del comportamiento de las funciones ¢ Máximos y mínimos. l l ¢ f(x) tiene un máximo en un punto x=a ↔ f(a-h) ≤f(a) ≥ f(a+h) f(x) tiene un mínimo en un punto x=a ↔ f(a-h) ≥ f(a)≤f(a+h) Continuidad. Discontinuidad. Una función f es continua cuando puede dibujarse sin levantar el lápiz del papel. Cada vez que sea necesario levantarlo para seguir dibujando se produce una discontinuidad. En todos los puntos en los que f no está definida se produce una discontinuidad, un salto de su gráfica.

Desarrollo Características del comportamiento de las funciones ¢ Funciones escalonadas. Son funciones definidas a trozos, constantes en cada trozo y discontinuas en los puntos de división de los intervalos. ¢ Simetrías: pares e impares. l l Una función es par si f(x)=f(-x) para todo x de su dominio. Las funciones pares son simétricas respecto del eje OY. Una función es impar si f(x)=-f(-x) para todo x de su dominio. Las funciones impares son simétricas respecto del origen de coordenadas.

Desarrollo Características del comportamiento de las funciones ¢ Periodicidad. Una función es periódica si hay algún número k tal que f(x+k)=f(x) para todo x. Esto significa que su gráfica se repite cada k unidades. El menor de los valores de k que cumpla esa condición es el periodo de la función. ¢ Asíntotas. Las asíntotas son rectas hacia las cuales tiende a pegarse la gráfica de la función; esto es, la curva correspondiente a la función se acerca cada vez más a una recta. Pueden ser verticales, horizontales y oblicuas. Las funciones de la forma P(x)/Q(x), pueden tener asíntotas verticales en aquellos puntos que anulen el denominador (Q(x)=0).

Desarrollo Funciones polinómicas ¢ Funciones polinómicas: l l l Constantes: f(x)=a Se representa mediante una recta horizontal. Lineales: f(x)=mx+n Se representan mediante una recta de pendiente m que pasa por el punto (0, n). A la función lineal también se le llama función afín. Cuadráticas: f(x)=ax²+bx+c, a≠ 0 Se representan mediante parábolas. Sus ejes son paralelos al eje Y. Su vértice es X 0=-b/2 a. Su forma depende del valor de a: Si a>0, las ramas van hacia arriba. Si a<0, las ramas van hacia abajo. De proporcionalidad directa: f(x)=kx k indica la razón de proporcionalidad. Su gráfica es la de una recta que pasa por el origen. Otras: f(x)= El dominio de existencia de las funciones polinómicas es . Si el polinomio es de grado n, tiene a lo sumo n raíces, que son los cortes con el eje de abscisas. Se representan mediante una línea “continua”.

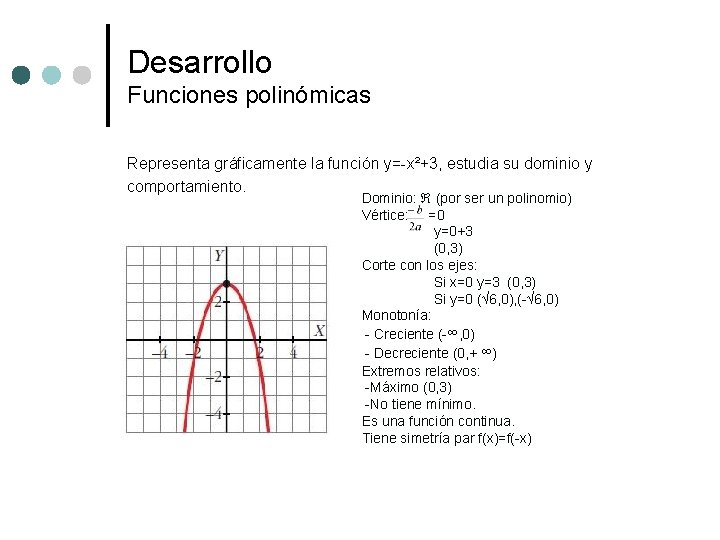
Desarrollo Funciones polinómicas Representa gráficamente la función y=-x²+3, estudia su dominio y comportamiento. Dominio: (por ser un polinomio) Vértice: =0 y=0+3 (0, 3) Corte con los ejes: Si x=0 y=3 (0, 3) Si y=0 (√ 6, 0), (-√ 6, 0) Monotonía: - Creciente (-∞, 0) - Decreciente (0, + ∞) Extremos relativos: -Máximo (0, 3) -No tiene mínimo. Es una función continua. Tiene simetría par f(x)=f(-x)

Desarrollo Funciones polinómicas EJERCICIOS PARA CLASE C 2. Representa gráficamente las siguientes funciones y estudia su comportamiento: a) y=-2 x+7, x Є (1, 4] b) y=x²-6 x+5 c) y=x²-4, x Є (-∞, 2) U (2, +∞) C 3. Una persona duda entre comprarse un coche de gasolina o uno de gasóleo. El primero consume, cada 100 km. 12 l. de gasolina a 0, 69 €/l. El segundo consume, cada 100 km. 7 l. de gasóleo a 0, 42 €/l. y cuesta 3005 € más que el otro modelo. Haz un estudio del gasto total según los kilómetros recorridos y averigua a partir de qué kilometraje resulta más rentable uno que el otro.

Desarrollo Funciones polinómicas EJERCICIOS PARA CASA K 1. Representa las siguientes funciones y estudia su comportamiento: a) y= x+4 b) y=x²-5 x+4 c) y=-2 x²+10 x-8 K 2. La altura de un objeto que es lanzado hacia arriba viene dada por la función h(t)=vt- gt², donde v es la velocidad con la que es lanzado, t el tiempo transcurrido y g la aceleración de la gravedad. Si lanzamos hacia arriba una pelota de tenis a 24, 5 m/s: a) ¿Qué altura tiene a los 2 segundos? b) ¿Cuándo vuelve a pasar por la misma altura que en el apartado anterior? c) ¿Cuál es la altura máxima que alcanza? d) ¿Cuántos segundos tarda en regresar al suelo? e) Representa su gráfica y, a partir de ella, indica su dominio y recorrido.

Desarrollo Funciones racionales ¢ Funciones racionales: Son de la forma P(x)/Q(x), donde P(x) y Q(x) son polinomios. La gráfica es una línea “continua” en los intervalos determinados por los puntos que anulan el denominador. Su dominio de existencia es excepto en los puntos que anulan al denominador Q(x). Si el polinomio del numerador P(x) es de grado n, tiene a lo sumo n raíces, que son los cortes con el eje de abscisas. La gráfica es una línea “continua” en los intervalos determinados por los puntos que anulan al denominador. Si los polinomios P(x) y Q(x) tienen el mismo grado, al dar valores muy grandes a x la función f(x) se “acerca” la recta y=a/b, donde a es el coeficiente principal de P(x) y b el de Q(x).

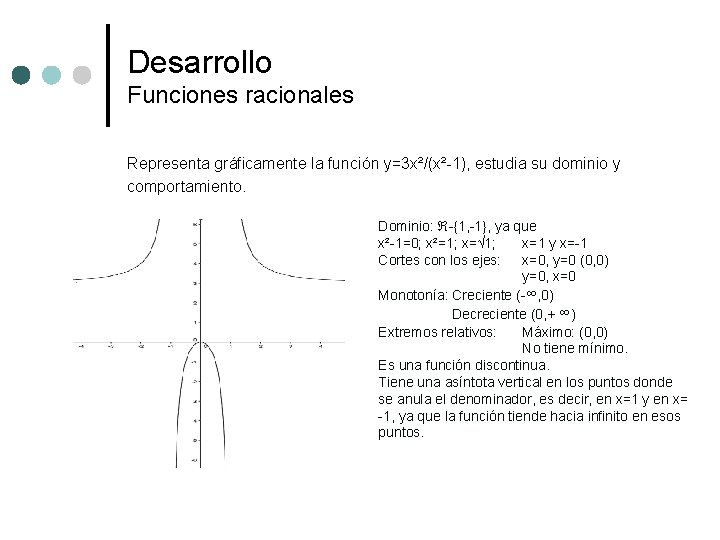
Desarrollo Funciones racionales Representa gráficamente la función y=3 x²/(x²-1), estudia su dominio y comportamiento. Dominio: -{1, -1}, ya que x²-1=0; x²=1; x=√ 1; x=1 y x=-1 Cortes con los ejes: x=0, y=0 (0, 0) y=0, x=0 Monotonía: Creciente (-∞, 0) Decreciente (0, + ∞) Extremos relativos: Máximo: (0, 0) No tiene mínimo. Es una función discontinua. Tiene una asíntota vertical en los puntos donde se anula el denominador, es decir, en x=1 y en x= -1, ya que la función tiende hacia infinito en esos puntos.

Desarrollo Funciones racionales EJERCICIOS PARA CLASE C 4. Representa gráficamente y estudia su comportamiento: a) f(x)=1/(2 x+1) b) g(x)=2 x/(3 x+1) c) h(x)=x/(x²-1) EJERCICIO PARA CASA (INVESTIGACIÓN) K 3. Busca información sobre las gráficas de la Bruja de Agnesi, invéntate una, represéntala y estudia su comportamiento.

Desarrollo Funciones radicales ¢ Funciones radicales: Son de la forma y=n√f(x) (raíz n-ésima) Su dominio depende del índice de la raíz. Si el índice es impar, el dominio será todo , y si el índice es par, el dominio será aquellos valores de x para los cuales, el radicando sea positivo. Si el índice de la raíz es n, tiene a lo sumo n raíces, que son los cortes con el eje de abscisas. Se representan mediante un línea “continua”.

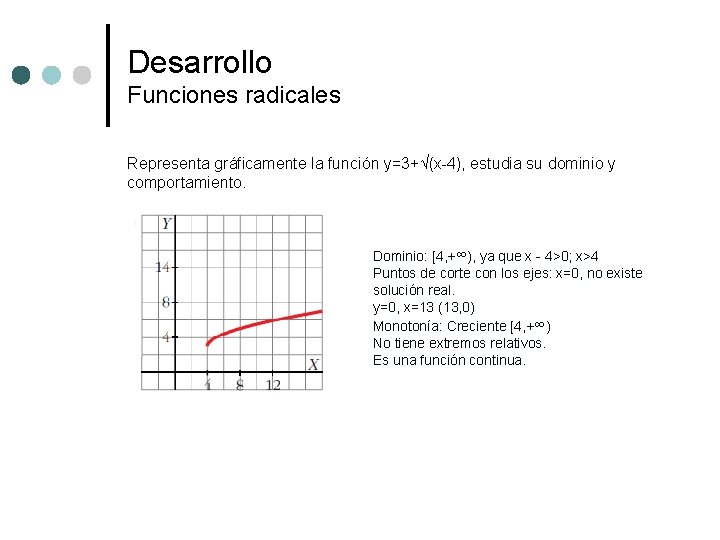
Desarrollo Funciones radicales Representa gráficamente la función y=3+√(x-4), estudia su dominio y comportamiento. Dominio: [4, +∞), ya que x - 4>0; x>4 Puntos de corte con los ejes: x=0, no existe solución real. y=0, x=13 (13, 0) Monotonía: Creciente [4, +∞) No tiene extremos relativos. Es una función continua.

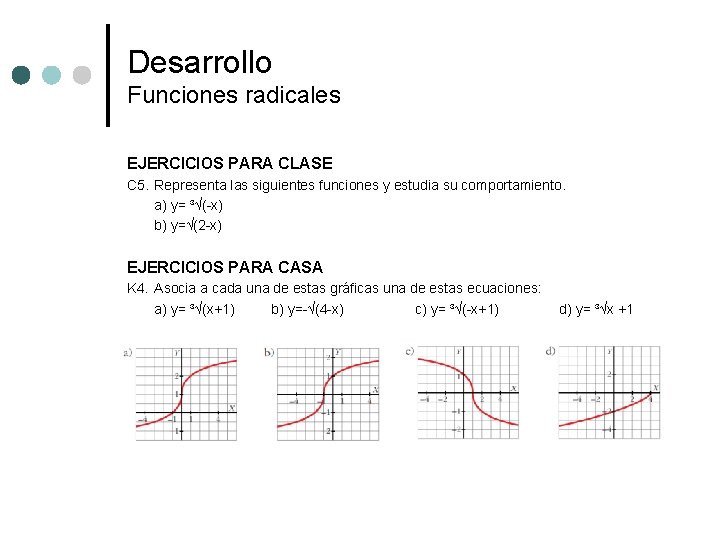
Desarrollo Funciones radicales EJERCICIOS PARA CLASE C 5. Representa las siguientes funciones y estudia su comportamiento. a) y= ³√(-x) b) y=√(2 -x) EJERCICIOS PARA CASA K 4. Asocia a cada una de estas gráficas una de estas ecuaciones: a) y= ³√(x+1) b) y=-√(4 -x) c) y= ³√(-x+1) d) y= ³√x +1

Desarrollo Funciones a trozos ¢ Definidas a trozos: Aquellas definidas por expresiones distintas en intervalos distintos. Se representan, tramo a tramo, prestando atención a su comportamiento en los puntos de empalme.

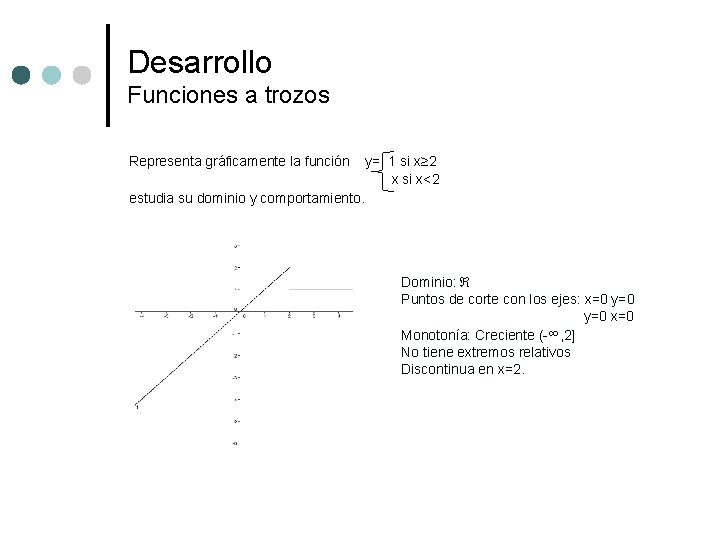
Desarrollo Funciones a trozos Representa gráficamente la función y= 1 si x≥ 2 x si x<2 estudia su dominio y comportamiento. Dominio: Puntos de corte con los ejes: x=0 y=0 x=0 Monotonía: Creciente (-∞, 2] No tiene extremos relativos Discontinua en x=2.

Desarrollo Funciones a trozos ¢ EJERCICIOS PARA CLASE C 6. Representa gráficamente la siguiente función y estudia su comportamiento: a) f(x)= 4 -x si x<1 x+4 si x>5 b) f(x)= x+1 si xЄ[-3, 0) x²-2 x+1 si xЄ[0, 3] 4 si xЄ(3, 7) C 7. Una agencia de viajes organiza un crucero por el Mediterráneo. El precio del viajes es de 1000 € si reúne entre 30 y 60 pasajeros; para un menor número de pasajeros el crucero se suspende. Pero si supera los 60, hace una rebaja de 10 € a cada participante por cada nuevo pasajero. a) Halla la función que da el precio del crucero dependiendo del número de viajeros. Represéntala gráficamente. b) Calcula la función que da el ingreso total que obtiene la agencia organizadora en función del número de viajeros. Represéntala gráficamente.

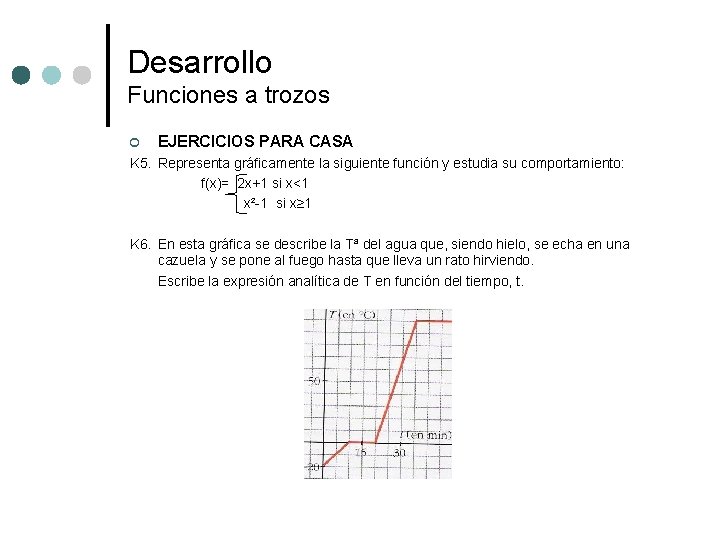
Desarrollo Funciones a trozos ¢ EJERCICIOS PARA CASA K 5. Representa gráficamente la siguiente función y estudia su comportamiento: f(x)= 2 x+1 si x<1 x²-1 si x≥ 1 K 6. En esta gráfica se describe la Tª del agua que, siendo hielo, se echa en una cazuela y se pone al fuego hasta que lleva un rato hirviendo. Escribe la expresión analítica de T en función del tiempo, t.

Desarrollo Algunas transformaciones de funciones ¢ Simetrías: -f(x) y f(-x) l La función –f(x) cambia de signo todos los resultados de f(x). Las gráficas de f(x) y –f(x) son simétricas respecto del eje OX. l La función f(-x) se obtiene sustituyendo x por –x en la fórmula de f(x). Esta función es la simétrica respecto del eje OY, de la función f(x) = x²-3 x+1 - f(x) = -x²+3 x-1 f(-x) = x²-3 x+1

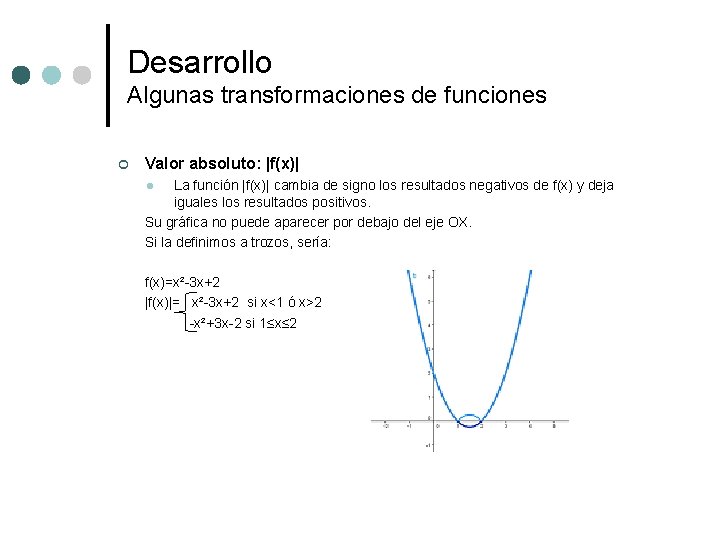
Desarrollo Algunas transformaciones de funciones ¢ Valor absoluto: |f(x)| La función |f(x)| cambia de signo los resultados negativos de f(x) y deja iguales los resultados positivos. Su gráfica no puede aparecer por debajo del eje OX. Si la definimos a trozos, sería: l f(x)=x²-3 x+2 |f(x)|= x²-3 x+2 si x<1 ó x>2 -x²+3 x-2 si 1≤x≤ 2

Desarrollo Algunas transformaciones de funciones ¢ Traslaciones: k+f(x) y f(x+k) l l La función k+f(x) suma el número k a los resultados de f(x). Si k es positivo, la gráfica se desplaza k unidades hacia arriba; si k es negativo, se desplazará k unidades hacia abajo. La función f(x+k) es la misma que f(x), pero trasladada k unidades a la izquierda si k es positivo y a la derecha si k es negativo. f(x)=x²-3 x+1 2+f(x)=x²-3 x+3 f(2+x)=(2+x)²-3(2+x)+1

Desarrollo Algunas transformaciones de funciones ¢ Dilataciones y contracciones: f(kx) y kf(x) l l La función f(kx) contrae o dilata la función f(x). Si k>1, se contrae; si 0<k<1, se dilata. La función kf(x) multiplica por k todos los resultados de f(x)=x²-3 x+1 g(x)=2 f(x)=2 x²-6 x+2 h(x)=f(2 x)=4 x²-6 x+1 f(x)= x²-3 x+1 g(x)=(1/2)x²-(3/2)x+1/2 h(x)=x²/4 -(3/2)x+1

Desarrollo Algunas transformaciones de funciones EJERCICIO PARA CLASE C 8. Para la función dada por la gráfica adjunta, representa las gráficas de las funciones: a) f(-x) b) |f(x)| c) 2 f(x) d) f(2 x) EJERCICIO PARA CASA K 7. Ésta es la gráfica de la función x²-2 x-3. Representa, a partir de ella, las funciones: a) g(x)=f(x)+3 b) h(x)=f(x+2) c) i(x)=-f(x) d) j(x)=|f(x)|

Desarrollo Funciones exponenciales ¢ Funciones exponenciales: Para comprenderlas mejor, resolvamos la siguiente actividad: Un laboratorio quiere saber en cualquier instante el número de bacterias presentes en su estudio en función de las horas transcurridas. Para ello, en el laboratorio saben que en el instante inicial solo tienen una bacteria y que ésta se duplica por mitosis en una hora. Determina: a) ¿Cuántas bacterias habrán al cabo de una hora? b) ¿Y al cabo de 3 horas? ¿Y al cabo de 5 horas? c) ¿Podrías dar la función que expresa el número de bacterias que habrán en el laboratorio al cabo de x horas?

Desarrollo Funciones exponenciales La función que expresa el número de bacterias presentes en el laboratorio en función de las horas transcurridas es f(x)= 2 x y su representación es la siguiente: Las funciones exponenciales son de la forma y= ax, siendo a>0 y a≠ 1. El dominio de las funciones exponenciales es . Son funciones continuas, y todas pasan por el punto (0, 1) y el (1, a). Si a>1, son funciones crecientes. Si 0<a<1, son decrecientes. El eje OX, la recta y=0, es asíntota horizontal , hacia - ∞ si a>1 o hacia + ∞ si 0<a<1.

Desarrollo Funciones exponenciales EJERCICIOS PARA CLASE C 9. Representa la función y=(1/2) x. ¿Qué relación existe entre dicha función y la función y=2 x? C 10. Dada la función y=ax, contesta razonadamente: a) ¿Puede ser negativa la variable x? ¿Y la variable y? b) ¿Para qué valores de a es la función creciente? c) ¿Cuál es el punto por el que pasan todas las funciones y=ax? d) ¿Son también exponenciales las funciones de la forma y=akx? En caso afirmativo, ¿cuál es la base de dichas funciones? EJERCICIOS PARA CASA K 8. Representa, en los mismos ejes de coordenadas, las funciones y= 3 x, y=3 x+1 y la función y=3 x-3. ¿Qué observas a partir del dibujo? K 9. De la función exponencial f(x)=kax conocemos que f(0)=5 y f(3)=40. a) ¿Es la función creciente o decreciente? b) ¿Cuánto valen k y a?

Desarrollo Funciones logarítmicas ¢ Funciones logarítmicas: Son las funciones inversas de las funciones exponenciales. Si tenemos la función exponencial y=a x su función inversa es y=log a x, siendo a>0 y a≠ 1. Su representación es la siguiente: El dominio de las funciones logarítmicas es aquel en el que su argumento es >0. Son continuas en su dominio y pasan por (1, 0) y (a, 1). Si a>1 son crecientes. Si 0<a<1 son decrecientes. El eje OY, la recta x=0, es asíntota vertical de su curva.

Desarrollo Funciones logarítmicas EJERCICIOS PARA CLASE C 11. ¿Cuál es el dominio de la función y=log 2 (2 -x)? Representa dicha función. C 12. En el contrato de trabajo de un empleado figura que su sueldo subirá un 6% anual. a) Si empieza ganando 10000 euros anuales, ¿cuánto ganará dentro de 10 años? b) Calcula cuánto tiempo tardará en duplicarse su sueldo. EJERCICIOS PARA CASA K 10. Calcula el dominio y representa, en los mismos ejes de coordenadas, la función f(x)=log 2 x, y, partir de ella, representa, calculando también su dominio, las funciones: a) g(x)=1+log 2 x b) h(x)=log 2(x-1) K 11. Dibuja la gráfica de la función y=log 3 x. Dibuja después, en los mismos ejes de coordenadas, la gráfica de la función y=log 1/3 x. ¿Qué relación existe entre ambas funciones?

Ejercicio de investigación V 1. Representa la gráfica que indica la hora del amanecer para tu ciudad en función del mes del año en curso. Para obtener datos entra en: http: //www. tutiempo. net/silvia_larocca/Programas/astronomia. htm Las coordenadas geográficas de tu ciudad has de buscarlas para poder realizar la actividad.

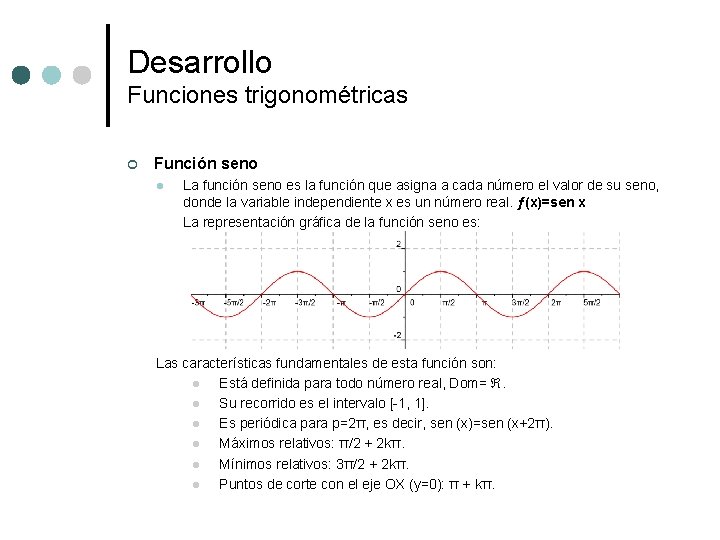
Desarrollo Funciones trigonométricas ¢ Función seno l La función seno es la función que asigna a cada número el valor de su seno, donde la variable independiente x es un número real. ƒ(x)=sen x La representación gráfica de la función seno es: Las características fundamentales de esta función son: l Está definida para todo número real, Dom= . l Su recorrido es el intervalo [-1, 1]. l Es periódica para p=2π, es decir, sen (x)=sen (x+2π). l Máximos relativos: π/2 + 2 kπ. l Mínimos relativos: 3π/2 + 2 kπ. l Puntos de corte con el eje OX (y=0): π + kπ.

Desarrollo Funciones trigonométricas ¢ Transformaciones de la función seno. Veamos la representación gráfica de algunas de las transformaciones de ƒ(x)=sen x (nos aparece siempre en rojo). l ƒ (x)= sen (-x) La función seno es impar porque ƒ (-x) = -ƒ(x) sen (-x) = -sen x, es simétrica respecto al origen. l ƒ (x)= sen (x-2) Traslación del tipo ƒ(x+k), es horizontal donde k = -2, como k es negativo, se desplaza ƒ(x), 2 unidades a la derecha para tener ƒ(x+k). l ƒ (x)= sen 2 x Contracción del tipo ƒ(kx), en horizontal donde k=2, como k>1 hay que contraer ƒ(x) para tener ƒ(kx).

Desarrollo Funciones trigonométricas ¢ Función coseno l La función coseno es la función que asigna a cada número el valor de su coseno, donde la variable independiente x es un número real. Dado que para cualquier número x sabemos que cos x= sen (x + π/2). La función ƒ(x)=cosx será idéntica a la del seno pero desplazada horizontalmente π/2 a la izquierda, así la representación gráfica es: Las características fundamentales de esta función se deducen de la del seno: l Está definida para todo número real, Dom= . l Su recorrido es el intervalo [-1, 1]. l Es periódica para p=2π, es decir, cos (x)=cos (x+2π). l Máximos relativos: 2 kπ. l Mínimos relativos: π+ 2 kπ. l Puntos de corte con el eje OX (y=0): π/2 + kπ.

Desarrollo Funciones trigonométricas ¢ Transformaciones de la función coseno. Veamos la representación gráfica de algunas de las transformaciones de ƒ(x)=cos x (nos aparece siempre en azul). l ƒ (x) = cos (-x) La función coseno es par porque ƒ (-x) = ƒ(x) cos (-x) = cos x, es simétrica respecto al eje OY. l ƒ (x) = 1/2 cos (x) Contracción del tipo kƒ(x), en vertical donde k=1/2, como k<1 hay que contraer ƒ(x) para tener kƒ(x).

Desarrollo Funciones trigonométricas ¢ Función tangente: l Como ya sabemos l Como conocemos las funciones de seno y coseno podemos sacar la función de la tangente a través de su tabla de valores. Una vez representada gráficamente, veamos sus características fundamentales: l Está definida para todo número real, excepto para los que el cos x = 0 (denominador de la fracción), Dom= - π/2 + kπ. l l Su recorrido es el intervalo (-∞, ∞ ). Es periódica para p=π, es decir, tg (x)=tg(x+π). Tiene asíntotas verticales para las rectas x=π/2 + kπ. Puntos de corte con el eje OX (y=0): π + kπ y en x=0.

Desarrollo Funciones trigonométricas EJERCICIOS PARA CLASE C 13. Representa gráficamente las siguientes funciones y expresa por escrito qué transformaciones han sufrido con respecto a las funciones originales y=sen x e y=cos x. a) b) y = -sen (x) y = cos (x)-2 EJERCICIOS PARA CASA K 12. Representa gráficamente las siguientes funciones y expresa por escrito qué transformaciones han sufrido con respecto a las funciones originales y=sen x, y=cos x e y=tg x. a) y = sen (x-2) c) y = cos (1/4)x e) y = 1 – tg x b) y = sen (3 x) d) y = cos (x/2) f) y = tg (x)-1 Indica además el dominio, el recorrido y dibuja su periodo en la gráfica.

Ejercicios de Geo. Gebra A continuación realizaremos una serie de ejercicios con Geogebra, además de aquellos que se han ido realizando en cada etapa de esta unidad. G 1. Dibuja las gráficas de f(x)=2 X y g(x)=3 X. Contesta razonadamente a las siguientes cuestiones: a) Estas gráficas se cortan en un punto, ¿cuál es? b) La gráfica de f está por debajo de la de g en un intervalo, ¿cuál es? c) La gráfica de f está por encima de la de g en un intervalo, ¿cuál es? G 2. Dibuja las gráficas de f(x)=log 2 x y g(x)=log 3 x. Contesta razonadamente a las siguientes cuestiones: a) Estas gráficas se cortan en un punto, ¿cuál es? b) La gráfica de f está por debajo de la de g en un intervalo, ¿cuál es? c) La gráfica de f está por encima de la de g en un intervalo, ¿cuál es?

Ejercicios de Geo. Gebra G 3. Les daremos a los alumnos un listado de funciones por grupos, les pediremos que vayan una a una, por orden, introduciéndolas en la aplicación informática y que escriban en su cuaderno las repuestas a las siguientes cuestiones: (se sentarán por parejas equilibradas) a) ¿Qué tipo de funciones son? b) Indica el dominio y el recorrido. c) Punto(s) de corte con los ejes OX y OY. d) Indica si tienen máximos, mínimos o asíntotas y cuáles son. e) Si existe alguna simetría. f) ¿Qué tipo de transformación ha sufrido con respecto a la función inicial? Razona tu respuesta. Nota: Hay que explicarles que si no ven en la gráfica el valor exacto que den un valor próximo.

Ejercicios propuestos P 1. Halla el dominio de las siguientes funciones: a) √(x²-9) c) -1/(x³-x²) b) 1/√(4 -x) d) 2 x/(x 4 -1) P 2. Asocia a cada una de estas parábolas una de estas ecuaciones: a) y=x²-2 b) y=-0, 25 x² c) y=(x+3)² d) y=-2 x²

Ejercicios propuestos P 3. Representa las siguientes funciones y estudia su comportamiento. a) y=0, 5 x² c) y=2 x²-4 b) y=-x²+3 d) y=-3 x²/2 P 4. Observando las gráficas de estas funciones, indica cuál es su dominio de definición y su recorrido. P 5. Representa gráficamente las siguientes funciones: a) y= -2 si x<0 x-2 si 0≤x<4 2 si x≥ 4 b) y= -2 x-1 si x<1 (3 x-15)/2 si x ≥ 1

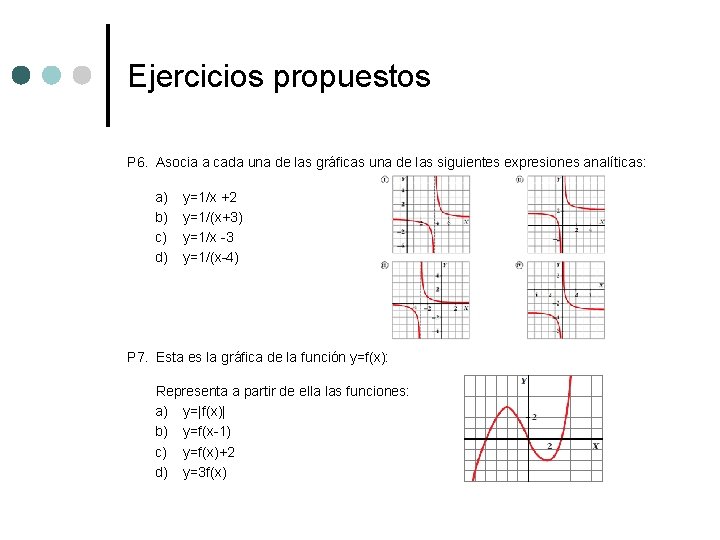
Ejercicios propuestos P 6. Asocia a cada una de las gráficas una de las siguientes expresiones analíticas: a) b) c) d) y=1/x +2 y=1/(x+3) y=1/x -3 y=1/(x-4) P 7. Esta es la gráfica de la función y=f(x): Representa a partir de ella las funciones: a) y=|f(x)| b) y=f(x-1) c) y=f(x)+2 d) y=3 f(x)

Ejercicios propuestos P 8. Representa y estudia el comportamiento de las siguientes funciones: a) y= -x-1 si x≤ 1 x²-2 si -1<x<1 x-1 si x ≥ 1 b) y= -x²/2 + 2 si x<1 x-3 si x ≥ 1 P 9. La factura del gas de una familia, en septiembre, ha sido 24, 82 euros por 12 m³, y en octubre, 43, 81 por 42 m³. a) Escribe la función que da el importe de la factura según los m³ consumidos y represéntala. b) ¿Cuánto pagarán si consumen 28 m³? P 10. Los gastos fijos mensuales de una empresa por la fabricación de x televisores son G = 3000 + 25 x, en miles de euros, y los ingresos mensuales son I = 50 x – 0, 02 x², también en miles de euros. ¿Cuántos televisores deben fabricarse para que el beneficio (ingresos menos gastos) sea máximo?

Ejercicios propuestos P 11. Una pelota es lanzada verticalmente hacia arriba desde lo alto de un edificio. La altura que alcanza viene dada por la fórmula h = 80 + 64 t – 16 t² (t en segundos y h en metros). a) Dibuja la gráfica en el intervalo [0, 5]. b) Halla la altura del edificio. c) ¿En qué instante alcanza su máxima altura? P 12. Representa y estudia el comportamiento de las siguientes funciones: a) y=1/(x+1) b) y=1/(x-1) c) y=-1/x d) y=1+1/x P 13. Representa y estudia el comportamiento de las siguientes funciones: a) y=√(x-1) b) y=-√(x+3) c) y=2+√x d) y=1 -√x

Ejercicios propuestos P 14. Elena va a visitar a su amiga Ana y tarda 20 minutos en llegar a su casa, que está a 1 km de distancia. Está allí media hora y en el camino de vuelta emplea el mismo tiempo que en el de ida. a) Representa la función tiempo-distancia. b) Busca su expresión analítica. P 15. Representa y define como funciones “a trozos”: a) y=|(x-3)/2| b) y=|3 x+6| c) y=|(2 x-1)/3| d) y=|-x-1| P 16. Calcula el dominio y los puntos de corte con los ejes de las siguientes funciones: a) f(x)=log(x+3) b) g(x)=log(x²+3) c) h(x)=log(-x²+x+2) P 17. Halla el dominio de definición de las siguientes funciones: a) f(x)=10 x-2 b) g(x)=10 1/(x-2 ) c) h(x)=10 √ (x-2)

Ejercicios propuestos P 18. El valor de la motocicleta Honda CBF 600 S que costaba 7200 € deprecia su valor en un 15 % anual. a) ¿Cuánto valdrá al cabo de 6 años? b) ¿Cuántos años han de transcurrir para que su valor sea inferior a 3500 €? P 19. Un fabricante aumenta el precio de sus productos según el IPC, que en los diez últimos años ha sufrido un crecimiento anual medio del 6%. a) ¿Cuál es el precio actual de un producto que hace diez años costaba 120 €? b) ¿Cuánto tiempo tardó el producto en costar el doble de lo que valía hace diez años? P 20. Se dice que en 1626 Peter Minuit compró la isla de Manhattan a los indios por 24 $. Imagina que Minuit hubiera puesto en el banco los 24 $ al 6% de interés compuesto. ¿Cuánto dinero tendría en 2011? Compara este resultado con el precio actual de la isla de Manhattan.

Ejercicios propuestos P 21. Un pueblo creció en forma exponencial de 10000 habitantes a 28900 habitantes en 2011. Suponiendo que continúa este tipo de crecimiento, ¿cuál sería la población en 2030? P 22. Representa con ayuda de la calculadora las siguientes funciones: a) f(x)=e 2 x-1 b) g(x)=log(x²+1) P 23. A partir de la gráfica de ƒ (x)= cos x, dibuja la gráfica de: a) ƒ (x)= -2 cosx b) ƒ (x)= 1+cos 2 x c) ƒ (x)= cos(x-π) P 24. El consumo de energía eléctrica de una familia, en kilovatios hora (k. Wh), viene dado por la siguiente función, , donde x indica los meses del año (enero=1): a) ¿Cuál es el consumo en enero, en julio y en octubre? b) ¿En qué mes consume más? ¿Y en cuál menos?

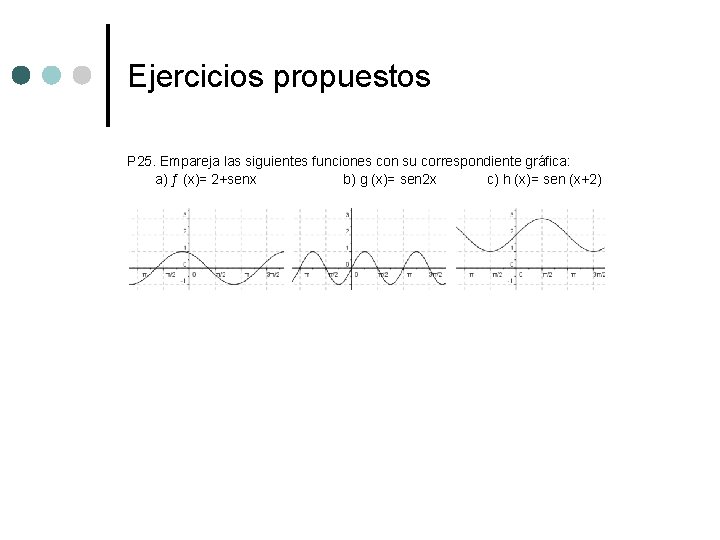
Ejercicios propuestos P 25. Empareja las siguientes funciones con su correspondiente gráfica: a) ƒ (x)= 2+senx b) g (x)= sen 2 x c) h (x)= sen (x+2)

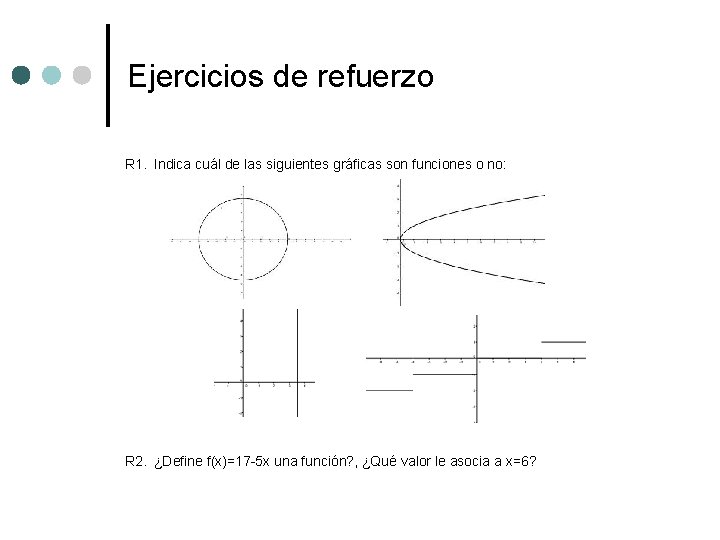
Ejercicios de refuerzo R 1. Indica cuál de las siguientes gráficas son funciones o no: R 2. ¿Define f(x)=17 -5 x una función? , ¿Qué valor le asocia a x=6?

Ejercicios de refuerzo R 3. Calcula el dominio y el recorrido de las funciones: R 4. Indica los intervalos de crecimiento y decrecimiento de las siguientes funciones: R 5. Indica los máximos y los mínimos relativos de las funciones del ejercicio anterior.

Ejercicios de refuerzo R 6. Representa las rectas: a) y=6 -2 x b) 2 x-3 y=12 c) x/4+y/5=1 R 7. Encuentra los puntos de corte de las rectas del ejercicio anterior con los ejes de coordenadas. R 8. Calcula las coordenadas del punto donde se cortan las funciones lineales y=2 x-5 e y=1 -x. R 9. Encuentra las coordenadas del vértice de las parábolas siguientes: a) y=x²+2 x-8 d) y=6 x²-7 x-5 b) y=-x²+7 x-10 e) y=3 x-2 x² c) y=4 x²-4 x+1 f) y=x²+2 x+3 R 10. Indica los puntos de corte con los ejes del ejercicio anterior.

Ejercicios de refuerzo R 11. Encuentra la expresión de la parábola que pasa por estos tres puntos (0, 1), (1, 0), (3, 10). R 12. Indica si los siguientes puntos pertenecen a la hipérbola y=12/x: A(12, 1), B(3, 24), C(-4, -3), D(120, 0), E(-6, 2), F(2, 5). R 13. Sea la función f(x)=log 3 x. Se pide: a) Halla el dominio de f(x). b) Halla f(1) y estudia el signo de f cerca de x=1. c) Comprueba que, tomando valores del dominio x 2>x 1, entonces f(x 2)>f(x 1) (la función es creciente en todo su dominio). d) Representa gráficamente f(x). R 14. Sea la función f(x)= 3 X : a) Halla el dominio de la función. b) Halla los cortes con los ejes y el signo de la función c) Comprueba que, tomando valores del dominio x 2>x 1, entonces f(x 2)>f(x 1) (la función es creciente en todo su dominio). d) Con la ayuda de una tabla de valores y los apartados anteriores, construye la gráfica de f. .

Ejercicios de refuerzo R 15. Calcula el dominio de las siguientes funciones: a) Ln(2 x-5) b) log(1 -x/x+3) c) 2 5/x² -4 R 16. A partir de la gráfica de f(x)=sen x, dibuja la gráfica de g(x) = sen (x+π/2). a) Marca en la gráfica el periodo que tiene g (x). b) ¿Cuántos máximos y mínimos tiene g(x) en el intervalo [0, 3π]? Indica sus abscisas. R 17. A partir de la gráfica de f(x)=cos x, dibuja las gráficas de: a) f(x)= 3 cos x b) f(x)= 2 – cos x

Ejercicios de ampliación A 1. Halla el dominio de las siguientes funciones: a) f(x)=(3 x²+x)/(x+1) e) f(x)= √(x-1)/(x-5) b) f(x)=(2 x-1)/(x²+x-12) f) f(x)= √(2 x-6)/ √(21 -3 x) c) f(x)=√(x²+4) g) f(x)=log(x²-x+2) d) f(x)=√(x²-25) h) f(x)= √[(x-3)/(x²-4)] A 2. Representa y define como funciones “a trozos”: a) y = |x² – 4| b) y = |x² – 2 x – 4| c) y = |– x²/2+ 2| d) y = |x² + 2 x – 2| A 3. Representa estas funciones y exprésalas en intervalos: a) y = 1 – |x| b) y = |x – 1| – |x|

Ejercicios de ampliación A 4. Estudia la simetría (par o impar o ninguna de las dos) de: a) f(x)=1/(x+1) c) f(x)=1/x+1 b) f(x)=1/(1 -x²) d) f(x)=2/(x³+4 x) A 5. Da valores a x (los mismos para las dos funciones) y representa en unos ejes de coordenadas las funciones f(x)=x-1; g(x)=(x²-1)/(x+1). ¿Qué observas? , ¿Qué pasa para x=-1? A 6. Dibuja la gráfica de y=log x, ¿Cómo obtendrías a partir de ella la gráfica de g(x)=2+log(x-3)? A 7. La altura de un objeto que es lanzado hacia arriba viene dada por la expresión h(t)=e 0+v 0 t-1/2 gt², donde e 0 es la altura desde donde se lanza, v 0 la velocidad inicial y la fuerza de la gravedad. a) ¿Cuándo alcanza su máxima altura? , b) ¿Cuál es esa altura máxima? , c) ¿Cuál es el valor de t máximo para que la función tenga sentido?

Ejercicios de ampliación A 8. Las tarifas de una empresa de transportes son: l 40 € por tonelada de carga si esta es menor o igual a 20 t. l Si la carga es mayor que 20 t, se restará de los 40 €, tantos € como toneladas sobrepasen 20. a) Dibuja la función ingresos de la empresa según la carga que transporte (carga máxima 30 t). b) Obtén la expresión analítica. A 9. Supongamos que el número de pulsaciones por minuto que es capaz de teclear una persona que aprende mecanografía viene dado por la función f(x)= (350(x+1))/(x+20), donde x expresa el número de horas de práctica (x≥ 0). a) ¿Cuántas pulsaciones por minuto tecleará al cabo de 1, 4, 10, 20, 30, 50 horas? b) ¿Es creciente f(x)? , ¿Alcanzará en algún momento las 400 pulsaciones por minuto? , ¿Tiende el número de pulsaciones hacia algún valor? c) Traza su gráfica.

Ejercicios de ampliación A 10. En una piscina hay un trampolín a 8 m de altura. Un nadador se lanza tomando impulso y elevándose 1 m antes de empezar a caer. El nadador alcanza el agua a 8 m del borde del trampolín. a) Si tomamos como origen de coordenadas la proyección del extremo del trampolín sobre el agua y el vértice de la parábola es (a, b), ¿cuánto vale b? b) La ecuación del movimiento es: y=k(x-a)² + 9. Justifícala y halla k y a. A 11. El carbono contiene un componente radioactivo, el carbono 14. Este último reduce su masa a la unidad cada 5500 años y se forma continuamente en las capas altas de la atmósfera por acción de rayos cósmicos de manera que se compensa el que se desintegra. Cada gramo de carbono contiene 10 -6 g de carbono 14 y en esta proporción es asimilado por los organismos vivos. Al morir éstos, el carbono 14 sigue desintegrándose. En ciertos fósiles se ha observado que 1 g de carbono contiene sólo 1, 3· 10 -11 g de carbono 14. ¿Puedes calcular su edad? .

Ejercicios de ampliación A 12. Partiendo de la gráfica ƒ(x)=sen x, y sabiendo que sen 2 x = 2 senx cosx, haz una representación gráfica de la función g (x) = senx cosx. A 13. La temperatura del aire, T, en grados centígrados, en una cierta ciudad, en un día de primavera, viene dada por la función: donde t es el tiempo medido en horas desde la medianoche. a) ¿Cuál es la temperatura a las 8 h, a las 12 h y a las 18 h? b) Representa gráficamente esta función. A 14. Supongamos que el número de linces en el Parque Natural de Doñana se puede expresar con la función, F(x)=40000+35000 sen(0’ 6 x), donde x es el tiempo en años desde la fecha de partida del estudio. El estudio de las fluctuaciones de su principal presa, la liebre, también varía sinusoidalmente con el mismo periodo. Se observó, sin embargo, que las liebres alcanzaban un máximo de 110000 individuos dos años antes que los linces alcanzarán el suyo, siendo el mínimo estimado de liebres de 10000. a) Halla la función f(x) que describa el número de liebres. b) Representa las funciones F(x) y f(x) e indica en el gráfico el momento en que ambas poblaciones son iguales.

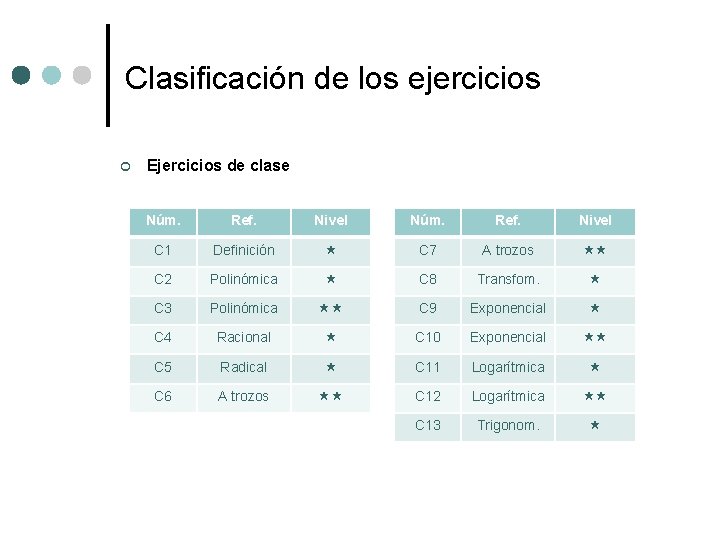
Clasificación de los ejercicios ¢ Ejercicios de clase Núm. Ref. Nivel C 1 Definición C 7 A trozos C 2 Polinómica C 8 Transfom. C 3 Polinómica C 9 Exponencial C 4 Racional C 10 Exponencial C 5 Radical C 11 Logarítmica C 6 A trozos C 12 Logarítmica C 13 Trigonom.

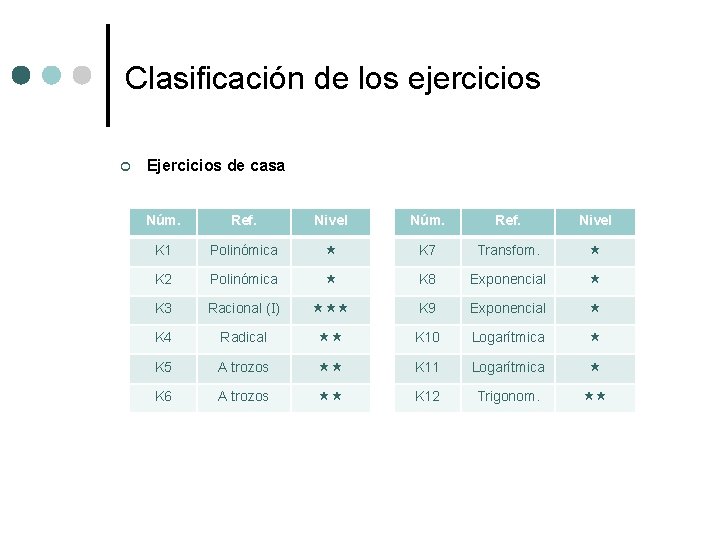
Clasificación de los ejercicios ¢ Ejercicios de casa Núm. Ref. Nivel K 1 Polinómica K 7 Transfom. K 2 Polinómica K 8 Exponencial K 3 Racional (I) K 9 Exponencial K 4 Radical K 10 Logarítmica K 5 A trozos K 11 Logarítmica K 6 A trozos K 12 Trigonom.

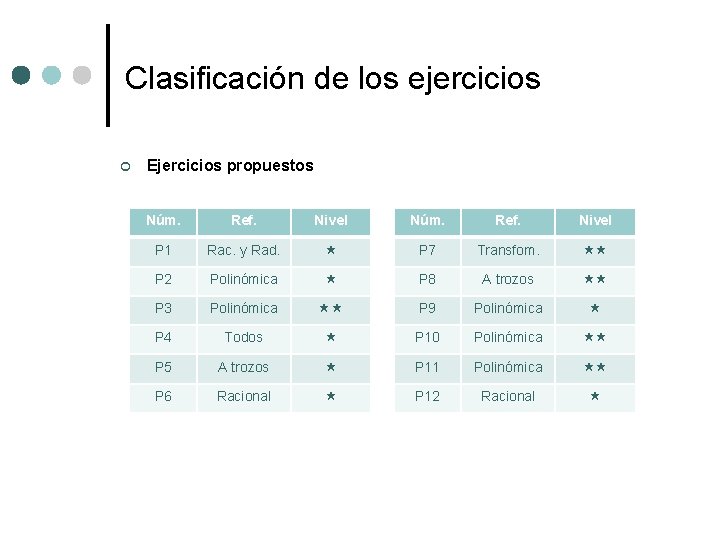
Clasificación de los ejercicios ¢ Ejercicios propuestos Núm. Ref. Nivel P 1 Rac. y Rad. P 7 Transfom. P 2 Polinómica P 8 A trozos P 3 Polinómica P 9 Polinómica P 4 Todos P 10 Polinómica P 5 A trozos P 11 Polinómica P 6 Racional P 12 Racional

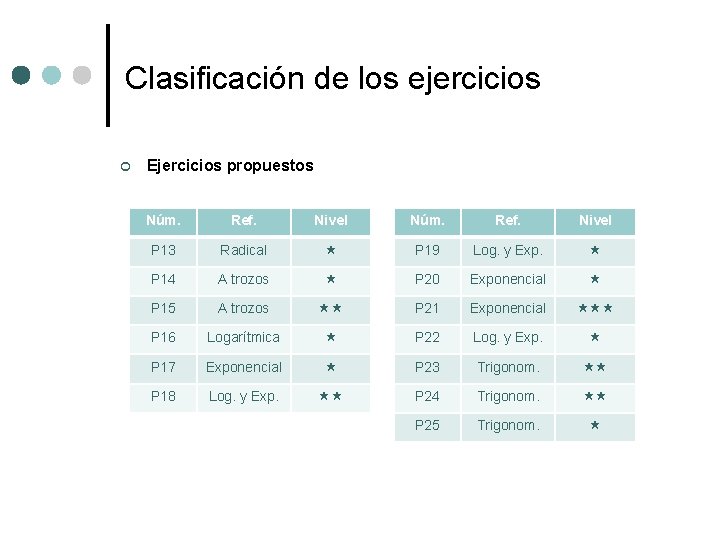
Clasificación de los ejercicios ¢ Ejercicios propuestos Núm. Ref. Nivel P 13 Radical P 19 Log. y Exp. P 14 A trozos P 20 Exponencial P 15 A trozos P 21 Exponencial P 16 Logarítmica P 22 Log. y Exp. P 17 Exponencial P 23 Trigonom. P 18 Log. y Exp. P 24 Trigonom. P 25 Trigonom.

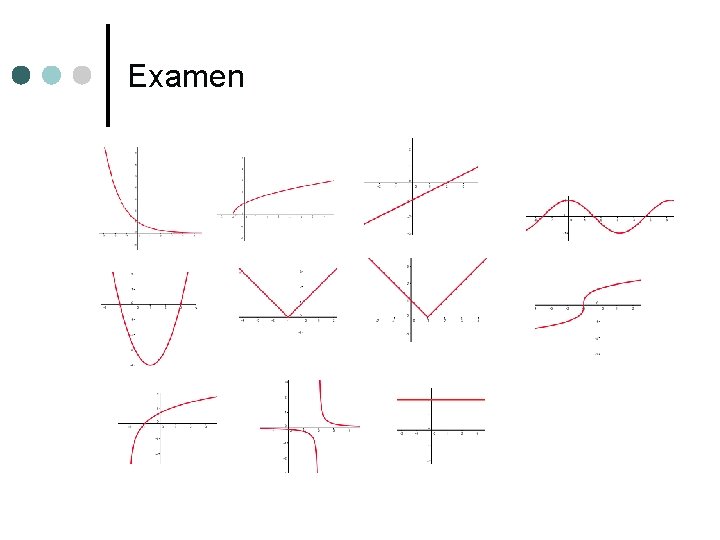
Examen E 1. Dos compañías de teléfono, C 1 y C 2 ofrecen las siguientes tarifas: l C 1 cobra 24 € fijos al mes y 0, 6 € por minuto desde el primer minuto. l C 2 cobra 57 € fijos al mes, que le dan derecho a 40 minutos gratis al mes y, a partir de los primeros 40 minutos, cada minuto más lo cobra un 5% más barato que la otra compañía. a) Escribe las expresiones de T 1(t) y T 2(t) que dan el precio a pagar en cada una de las compañías cuando se usa el teléfono t minutos al mes. b) Determina cuál es la compañía más ventajosa para el usuario, en función de los minutos que se use el teléfono al mes. E 2. Asocia a cada una de las gráficas una de las siguientes expresiones analíticas: a) y=2 g) y= 1 -x si x<1 b) y=-1+x/2 x-1 si x≥ 1 c) y=x²-2 x-3 h) y=|x+1| d) y=1/(4 x-8) i) y=(1/2) x e) y=√(x+1) j) y=sen(π/2+x) 1/3 f) y=(x+1) k) y=log(2+x)

Examen

Examen E 3. Representa gráficamente la siguiente función y estudia su comportamiento: f(x)= 2 x+1 si x<1 x²-1 si x≥ 1 E 4. El valor de un coche que costo 25000 euros, disminuye cada año el 20 % de su valor. a) Dibuja la función que representa la evolución del precio en relación a los años pasados. b) ¿Cuánto tiempo tiene que pasar para que el coche valga la mitad?

Recursos ¢ Los recursos que se utilizarán a lo largo de la unidad serán los siguientes: l l l Libro de texto. Calculadora. Aplicación informática: Geo. Gebra. Pizarra y tiza. Ordenador conexión a Internet.

El clima de clase ¢ Organización espacial l ¢ El alumnado se sentará por parejas, tomando como criterio para formar las parejas sentarlos de manera que el rendimiento académico sea dispar, de manera que el alumnado más aventajado pueda ayudar a aquellos que presenten mayores dificultades académicas, siendo el profesor quien decida dichas parejas y, si lo estimara necesario, quien realiza alguna modificación posteriormente. Atención a la diversidad Se tendrán en cuenta las siguientes pautas de atención a la diversidad: l Actividades de refuerzo para los alumnos que presenten mayores dificultades para adquirir los contenidos de la unidad. l Actividades de ampliación, para aquellos alumnos cuyas destrezas y rendimiento sean elevados. l Actividades de recuperación para el alumnado que no adquiera los conocimientos mínimos para aprobar la unidad. Si se presentan alumnos con algún tipo de discapacidad, se les atenderá consultando con el protocolo del centro e intentando actuar en la medida de lo posible para atender sus necesidades.

Evaluación ¢ Criterios de evaluación Los criterios de evaluación para el alumnado quedan detallados a partir de la ponderación que se muestra a continuación: l Una prueba de carácter teórico y práctico que constituirá el 60% de la nota. l El trabajo y la participación en clase también se tendrá en cuenta y su peso será del 15%. l El trabajo en casa contará también un 15% de la nota. l Las tareas de investigación y ampliación serán valoradas con el 10% de la nota. ¢ Mecanismos de recuperación El alumnado que tras finalizar la unidad presente una nota inferior a 5 deberá realizar un examen de recuperación, para el cual será requisito indispensable la entrega previa de las actividades de refuerzo. ¢ Evaluación del profesor Tras la finalización de la unidad didáctica se valorarán los distintos aspectos de ésta, y se mejorarán aquellas partes que se consideren oportunas, tanto conceptualmente como en su forma de desarrollo.

Bibliografía y webgrafía l l l l l Algoritmo 1, Bachillerato. Ed. SM. Matemáticas I, Bachillerato. Ed. Vicens-Vives. Matemáticas I, Bachillerato. Ed. Anaya. Matemáticas I, Bachillerato. Ed. Mc. Graw-Hill. Matemáticas I, Bachillerato. Ed. La Ñ – Proyecto Ajimez. Servicio de publicaciones de la S. A. E. M. Thales. http: //www. amejor. com/index. php? option=com_content&view=article&id=204: leibniz&catid=20: matemcos&Itemid=16 http: //www. solociencia. com/cientificos/isaac-newton-metodo-fluxiones. htm http: //www. tutiempo. net/silvia_larocca/Programas/astronomia. htm http: //www. iescanovas. es/documentos/programaciones 1011/MATEMATICAS/Programacion%204 -ESO. pdf