ESTRUCTURAS Anlisis Estructural Barras y Nodos B 3

ESTRUCTURAS

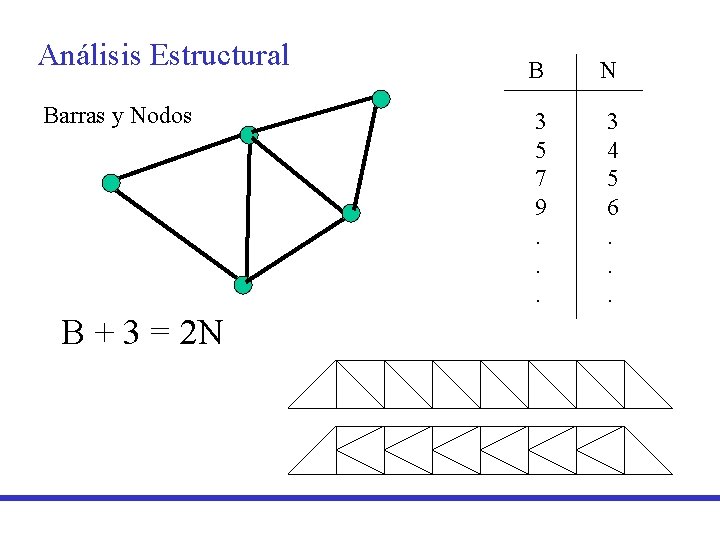
Análisis Estructural Barras y Nodos B + 3 = 2 N B N 3 5 7 9. . . 3 4 5 6. . .

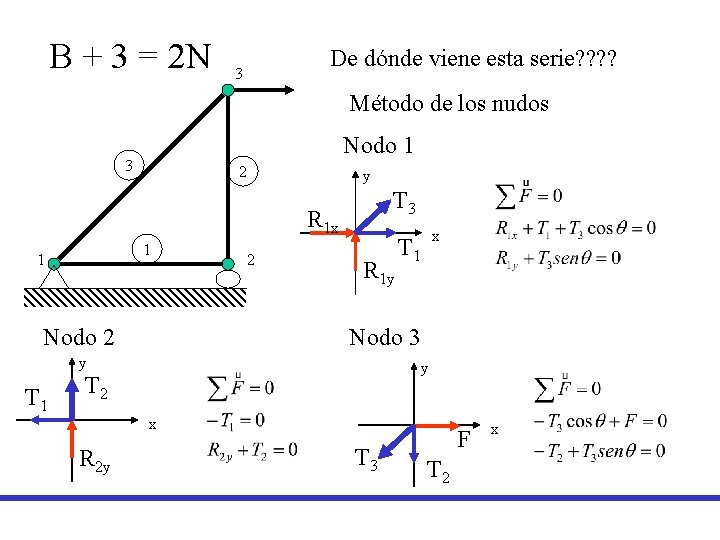
B + 3 = 2 N De dónde viene esta serie? ? 3 Método de los nudos Nodo 1 3 2 y T 3 R 1 x 1 1 Nodo 2 2 R 1 y Nodo 3 y T 1 x T 1 y T 2 x R 2 y T 3 F T 2 x

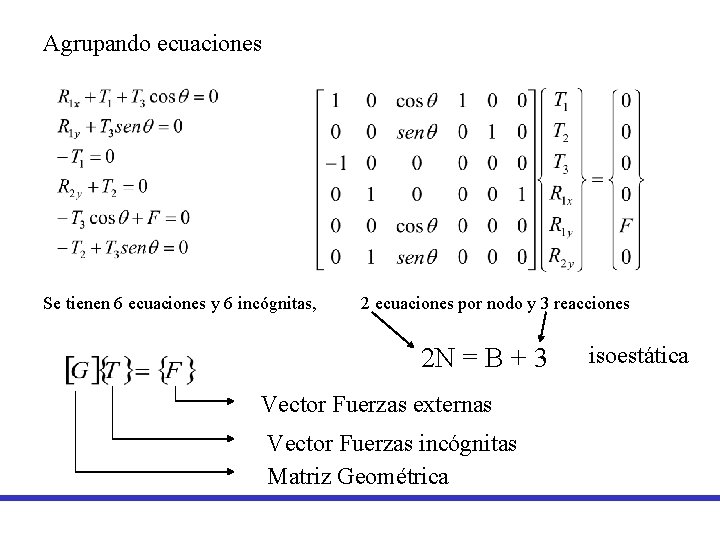
Agrupando ecuaciones Se tienen 6 ecuaciones y 6 incógnitas, 2 ecuaciones por nodo y 3 reacciones 2 N = B + 3 Vector Fuerzas externas Vector Fuerzas incógnitas Matriz Geométrica isoestática

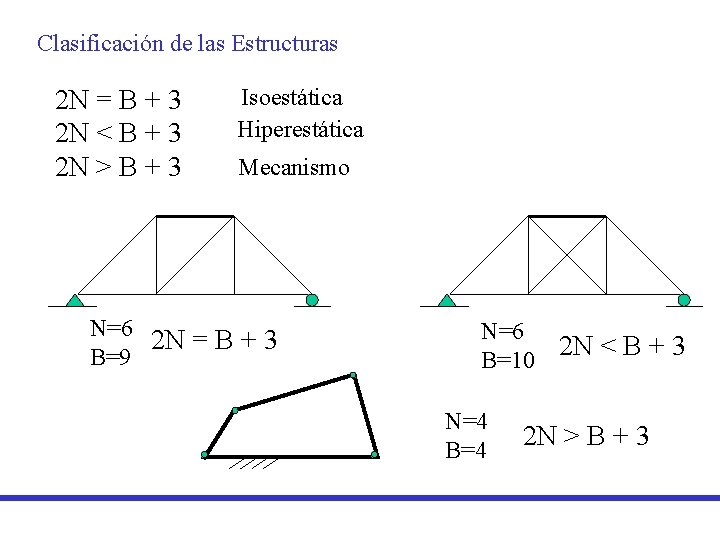
Clasificación de las Estructuras 2 N = B + 3 2 N < B + 3 2 N > B + 3 Isoestática Hiperestática Mecanismo N=6 2 N = B + 3 B=9 N=6 B=10 N=4 B=4 2 N < B + 3 2 N > B + 3

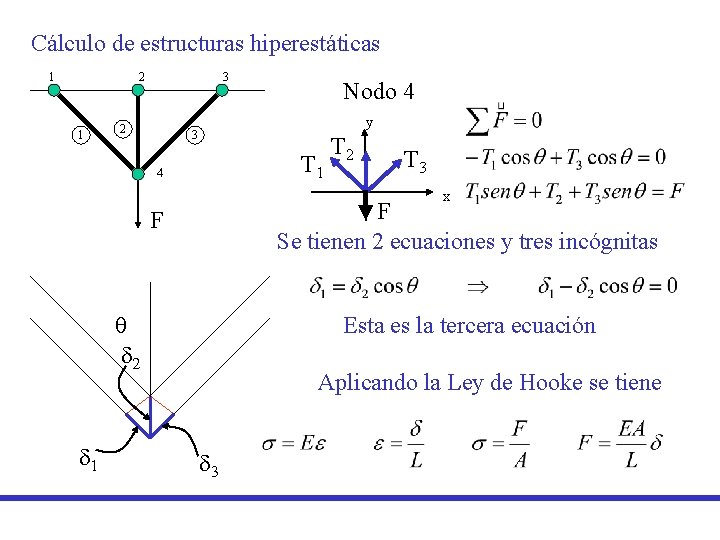
Cálculo de estructuras hiperestáticas 1 2 1 3 2 Nodo 4 y 3 T 1 4 T 2 T 3 x F Se tienen 2 ecuaciones y tres incógnitas F q d 2 d 1 Esta es la tercera ecuación Aplicando la Ley de Hooke se tiene d 3

Reemplazando en las ecuaciones de equilibrio se tiene: Escrito en forma matricial se tiene:

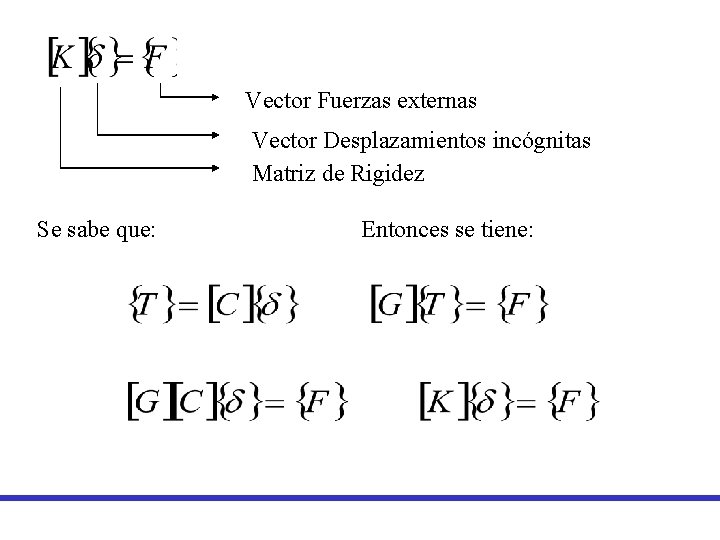
Vector Fuerzas externas Vector Desplazamientos incógnitas Matriz de Rigidez Se sabe que: Entonces se tiene:

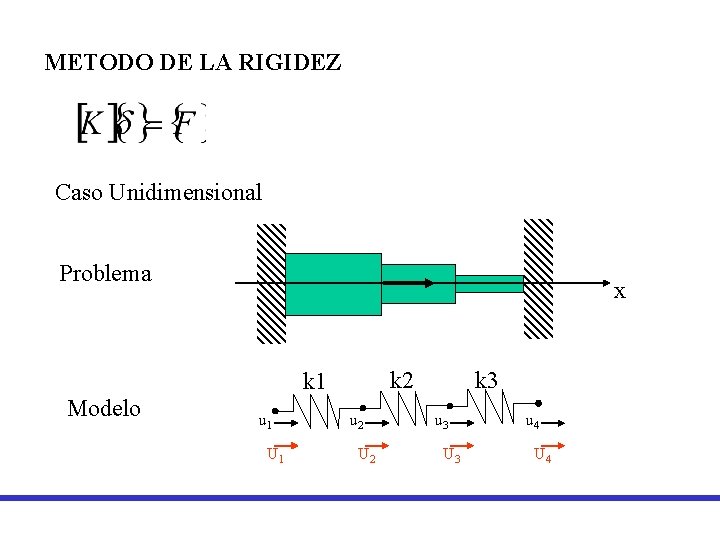
METODO DE LA RIGIDEZ Caso Unidimensional Problema x k 2 k 1 Modelo u 1 U 1 u 2 U 2 k 3 u 3 U 3 u 4 U 4

Para cada elemento k 1 u 2 U 11 U 12 k 2 u 3 U 22 U 23 k 3 u 4 U 33 U 34

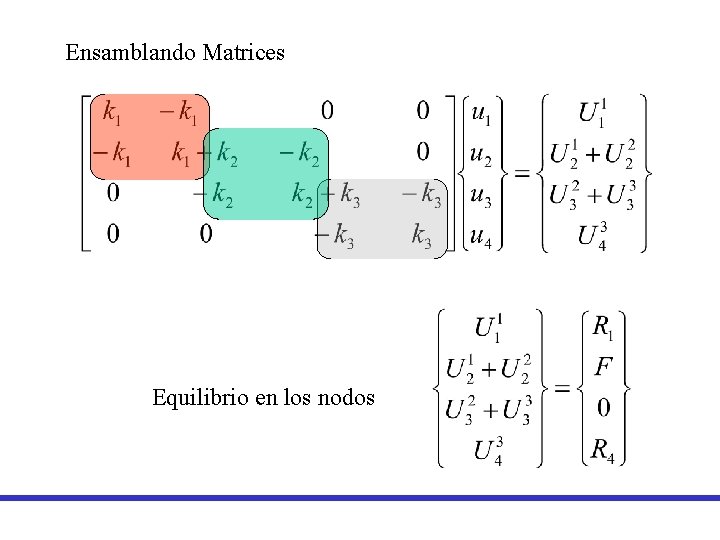
Ensamblando Matrices Equilibrio en los nodos

Si hacemos k 1= k 2= k 3=k tenemos

Aplicando condiciones de borde u 1=0 y u 4=0 se tiene:

Volviendo al problema 2 F/3 u 1=0 y u 4=0 2 F/3

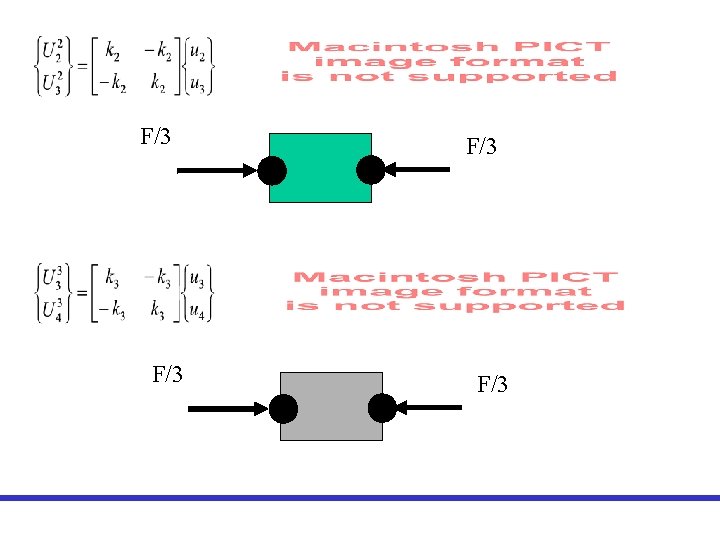
F/3 F/3

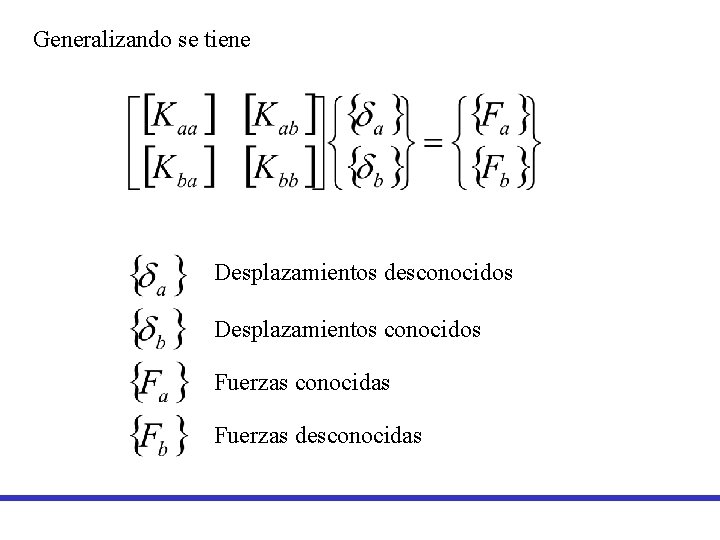
Generalizando se tiene Desplazamientos desconocidos Desplazamientos conocidos Fuerzas conocidas Fuerzas desconocidas

Resolviendo la primera fila se tiene Resolviendo la segunda fila se tiene

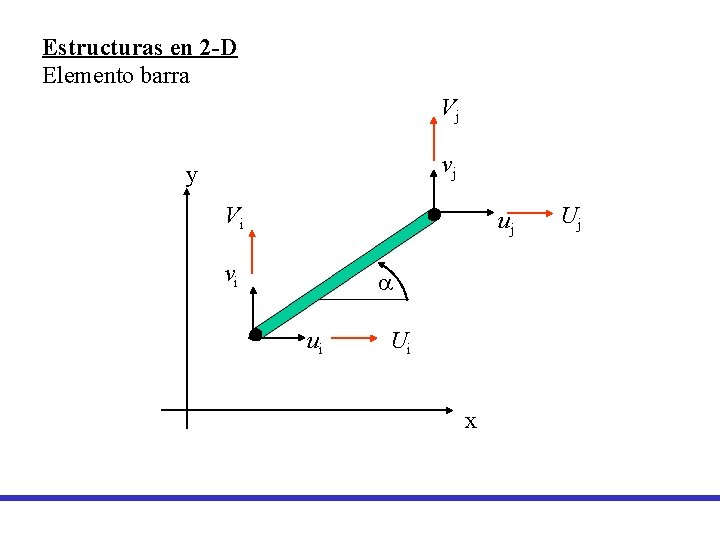
Estructuras en 2 -D Elemento barra Vj vj y Vi uj vi a ui Ui x Uj

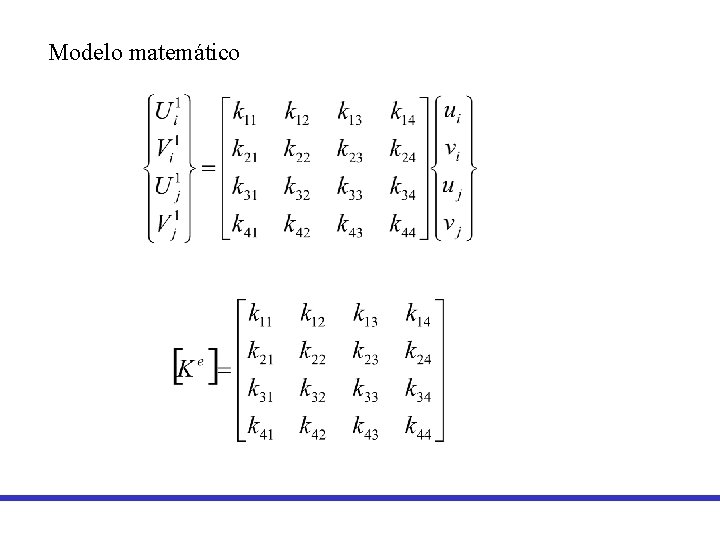
Modelo matemático

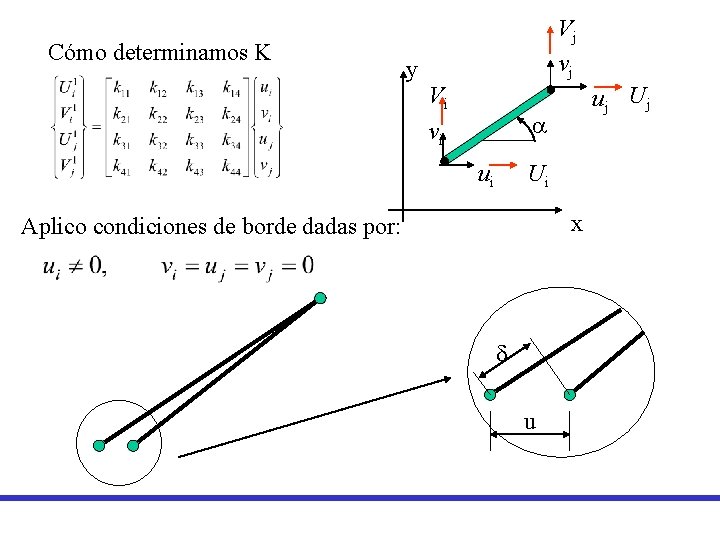
Cómo determinamos K y Vj vj Vi uj Uj a vi Ui ui x Aplico condiciones de borde dadas por: d u

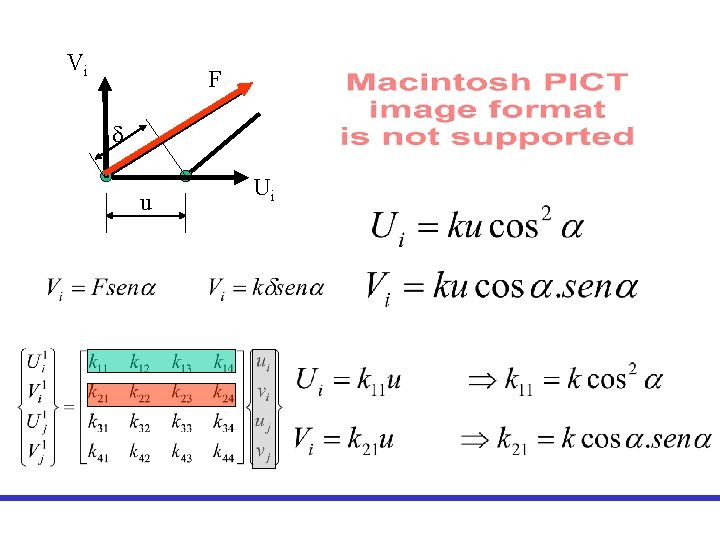
Vi F d u Ui

Para las otras columnas se procede con las siguientes condiciones de borde

MATRIZ de RIGIDEZ en 2 -D

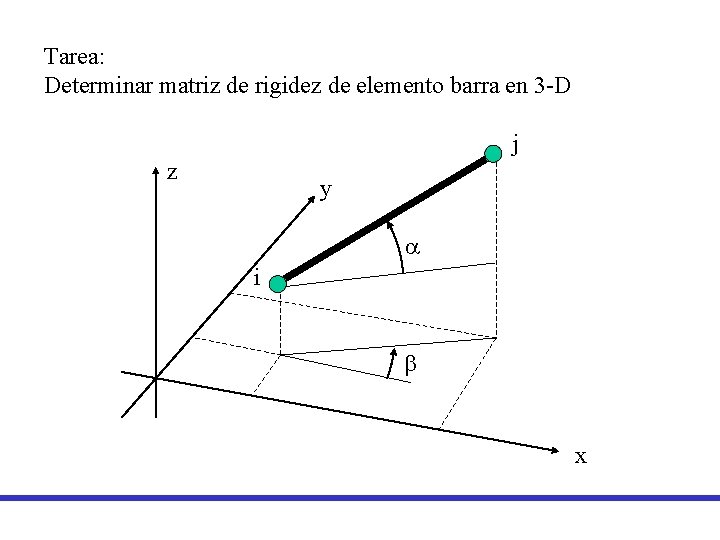
Tarea: Determinar matriz de rigidez de elemento barra en 3 -D j z y a i b x

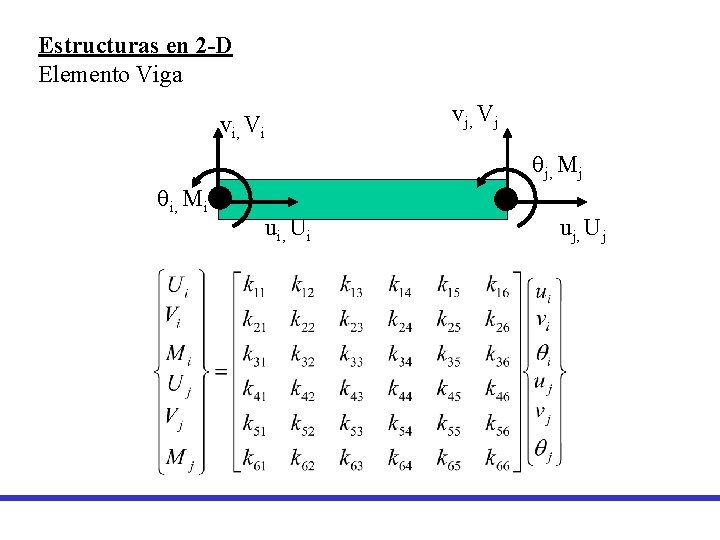
Estructuras en 2 -D Elemento Viga vi, Vi vj, Vj qj, Mj qi, Mi ui, Ui uj, Uj

Determinación de los coeficientes Observe que los Gd. L correspondientes a U, son los que cuantifican la tracción y compresión, además nunca producirán flexión. Por lo tanto hay una total independencia con las otras variables.

Determinación de los coeficientes Condiciones de borde dadas por: vj, Vj vi, Vi qi, Mi Ecuaciones: x qj, Mj x

Aplicando a condiciones de borde a las ecuaciones se tiene

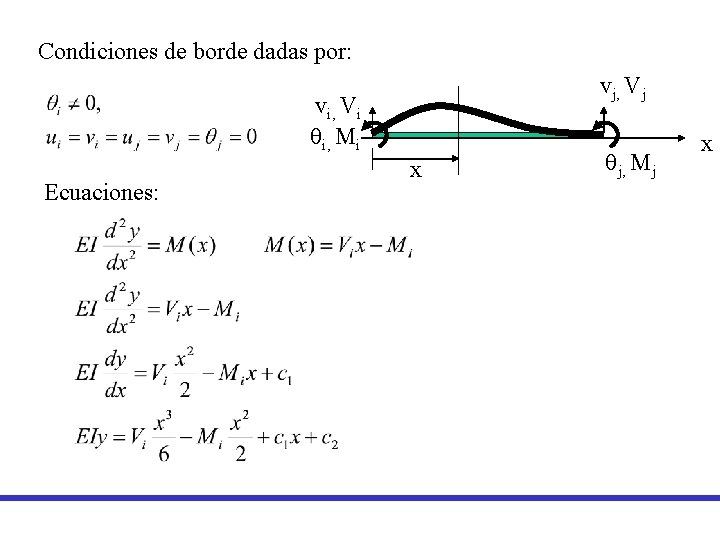
Condiciones de borde dadas por: vj, Vj vi, Vi qi, Mi Ecuaciones: x qj, Mj x

Aplicando a condiciones de borde a las ecuaciones se tiene

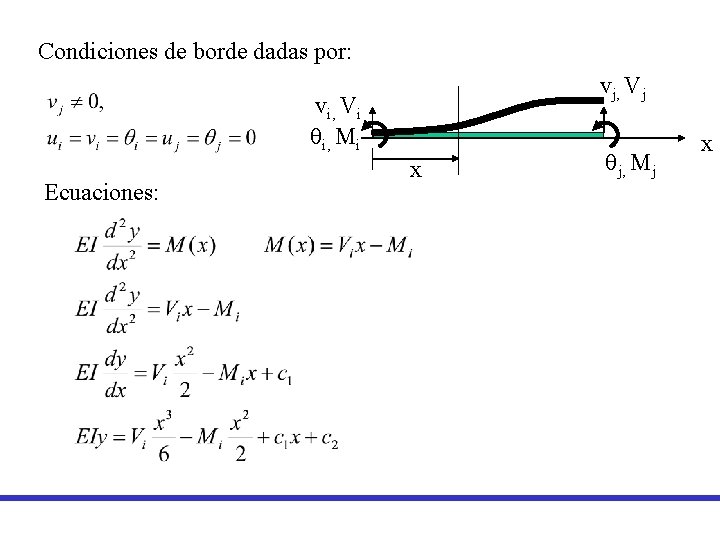
Condiciones de borde dadas por: vj, Vj vi, Vi qi, Mi Ecuaciones: x qj, Mj x

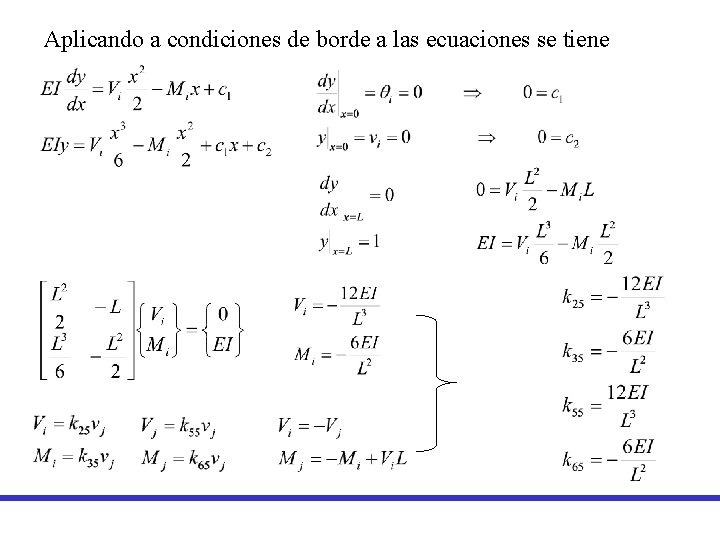
Aplicando a condiciones de borde a las ecuaciones se tiene

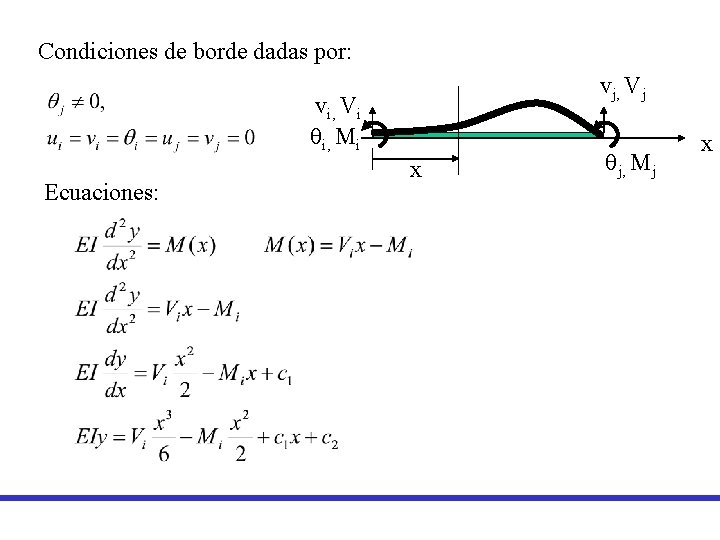
Condiciones de borde dadas por: vj, Vj vi, Vi qi, Mi Ecuaciones: x qj, Mj x

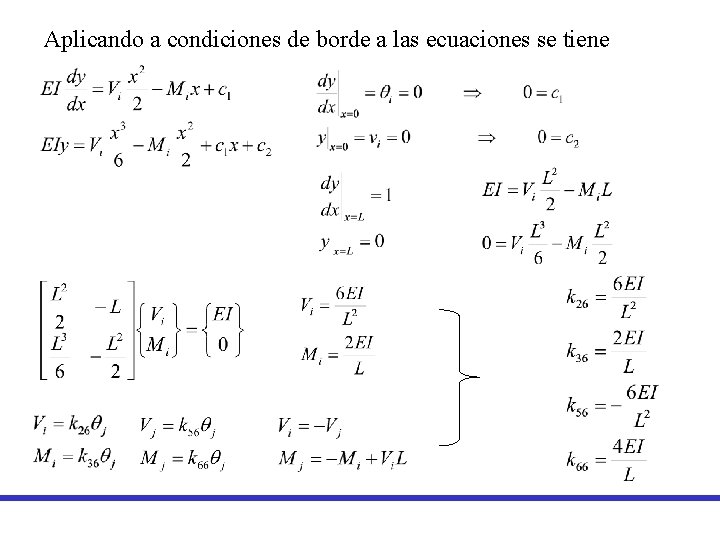
Aplicando a condiciones de borde a las ecuaciones se tiene

Matriz de rigidez Elemento Viga

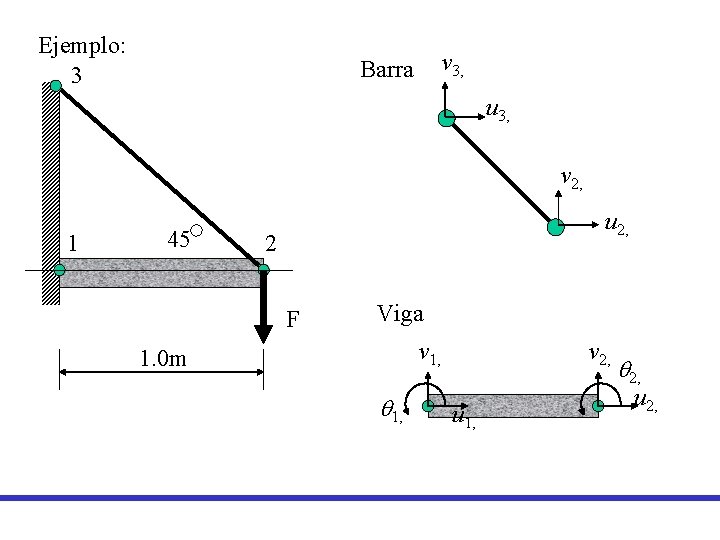
Ejemplo: 3 v 3, Barra u 3, v 2, 1 45 u 2, 2 F Viga v 1, 1. 0 m q 1, v 2, u 1, q 2, u 2,

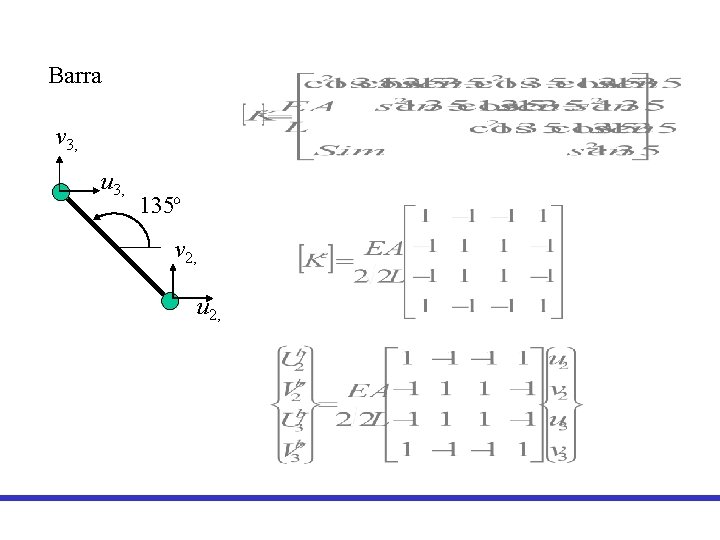
Barra v 3, u 3, 135 v 2, u 2,

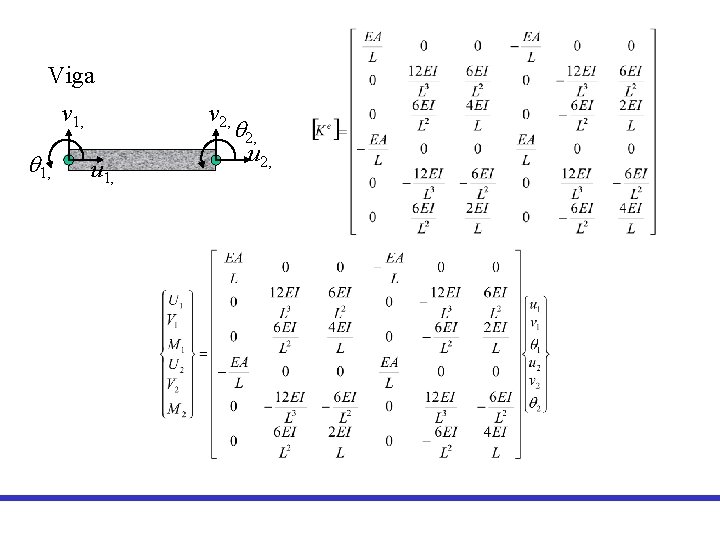
Viga v 1, q 1, v 2, u 1, q 2, u 2,

Ensamble de matrices

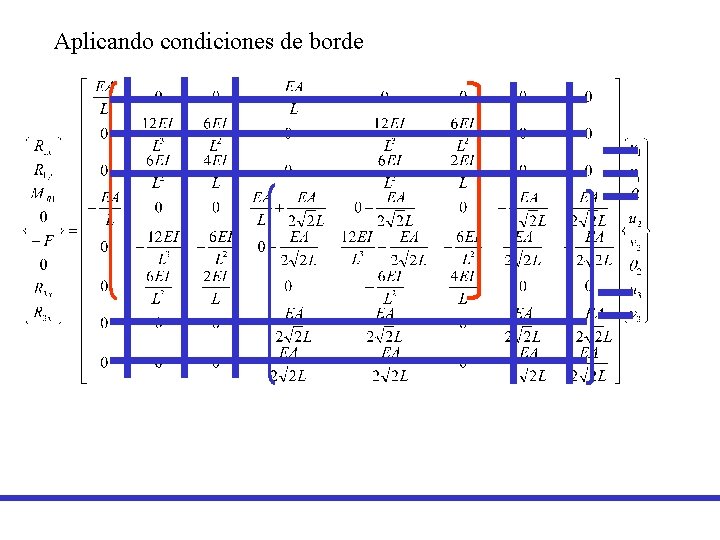
Aplicando condiciones de borde

F=10000 E=2. 0 x 1011 Pa L= 1. 0 m A=0. 01 m 2 Ab=0. 001 m 2 I=8. 33 x 10 -6 m 4

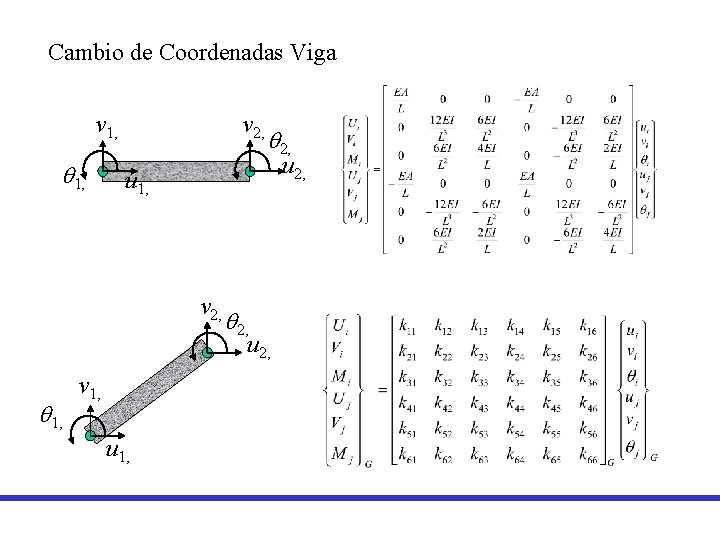
Cambio de Coordenadas Viga v 1, q 1, v 2, q 2, u 2, q 1, v 1, u 1,

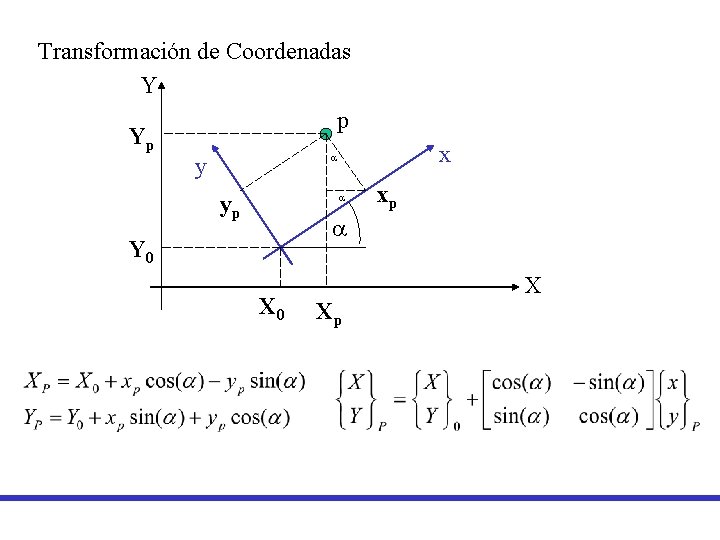
Transformación de Coordenadas Y p Yp a y yp a x xp a Y 0 X Xp

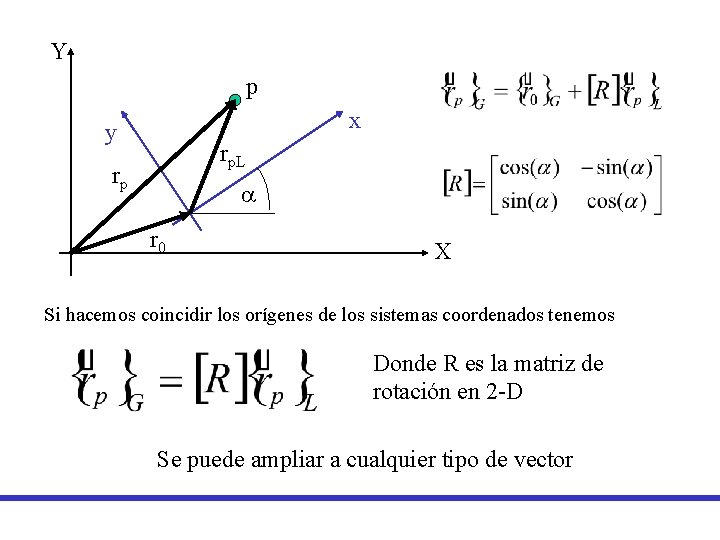
Y p x y rp. L rp a r 0 X Si hacemos coincidir los orígenes de los sistemas coordenados tenemos Donde R es la matriz de rotación en 2 -D Se puede ampliar a cualquier tipo de vector

Si se trata de fuerzas tenemos Observe que R es una matriz ortogonal, entonces su inversa es igual a la traspuesta. Por otra parte se tiene

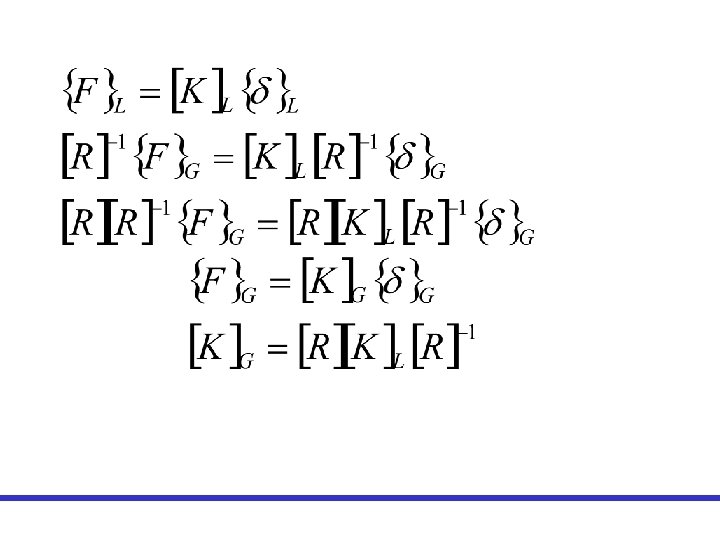
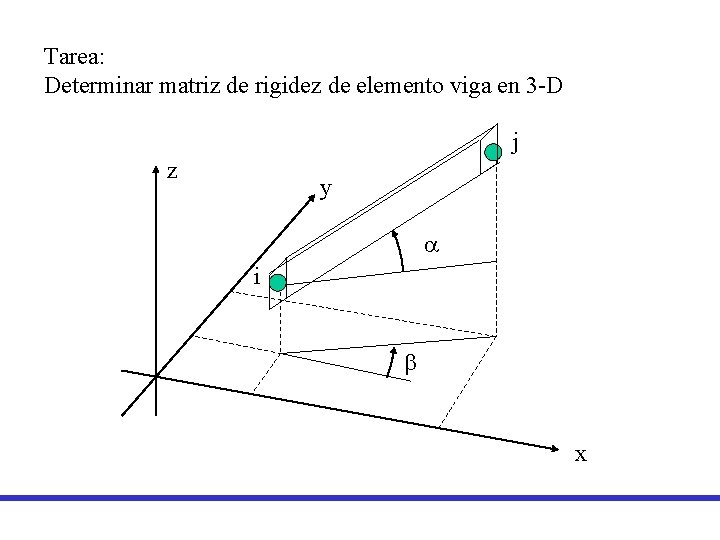
Tarea: Determinar matriz de rigidez de elemento viga en 3 -D j z y a i b x