Estratgias de Particionamento e Diviso e Conquista Estratgias

Estratégias de Particionamento e Divisão e Conquista

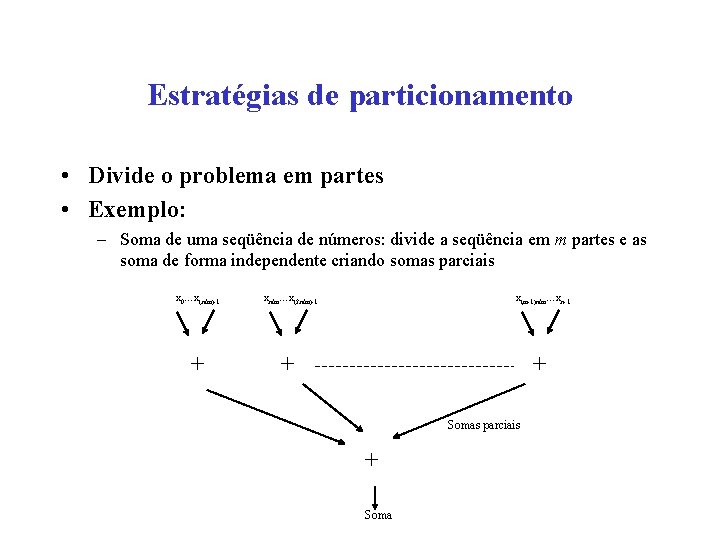
Estratégias de particionamento • Divide o problema em partes • Exemplo: – Soma de uma seqüência de números: divide a seqüência em m partes e as soma de forma independente criando somas parciais x 0…x(n/m)-1 xn/m…x(2 n/m)-1 x(m-1)n/m…xn-1 + + + Somas parciais + Soma

Utilizando send()s e receive()s separados • Mestre s = n/m; for (i=0, x=0; i < m; i++, x=x+s) send (&numbers[x], s, Pi); sum = 0; for (i=0; i < m; i++) { recv(&part_sum, Pany); sum=sum+part_sum; } • Escravo recv(numbers, s, Pmaster); part_sum=0; for (i=0; i < s; i++) part_sum=part_sum+numbers[i]; send (&part_sum, Pmaster); }

Utilizando rotina broadcast() • Mestre s = n/m; bcast(numbers, s, Pslave_group); sum = 0; for (i=0; i < m; i++) { recv(&part_sum, Pany); sum=sum+part_sum; } • Escravo bcast(numbers, s, Pmaster); start=slave_number * s; end=start + s; part_sum=0; for (i=start; i < end; i++) part_sum=part_sum+numbers[i]; send (&part_sum, Pmaster);

Utilizando rotinas scatter() e reduce() • Mestre s = n/m; scatter(numbers, &s, Pgroup, root=master); reduce_add(&sum, &s, Pgroup, root=master); • Escravo scatter(numbers, &s, Pgroup, root=master); . . reduce_add (&part_sum, &s, Pgroup, root=master);

Análise de complexidade • Seqüencial: n-1 somas • Paralela: Utilizando rotinas send e receive – Fase 1: Comunicação – Fase 2: Computação – Fase 3: Comunicação: retorno dos resultados parciais – Fase 4: Computação: acumulação final – Tempo total de execução: Pior que seqüencial

Divisão e conquista • Divide o problema em subproblemas que são da mesma forma que o problema maior e divisões posteriores podem ser realizadas por recursão • Exemplo – Uma definição recursiva seqüencial para adicionar uma lista de números int add (int *s) { if (number(s) <= 2) return (n 1 + n 2); else { divide (s, s 1, s 2); part_sum 1 = add(s 1); part_sum 2 = add(s 2); return(part_sum 1 + part_sum 2); } }

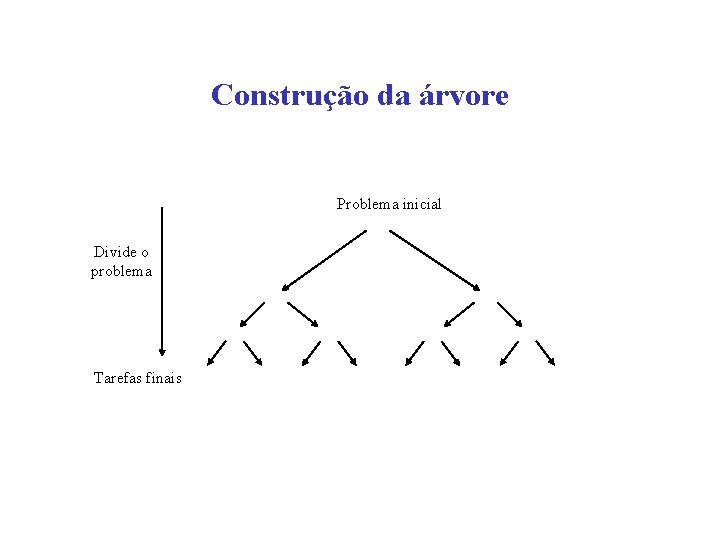
Construção da árvore Problema inicial Divide o problema Tarefas finais

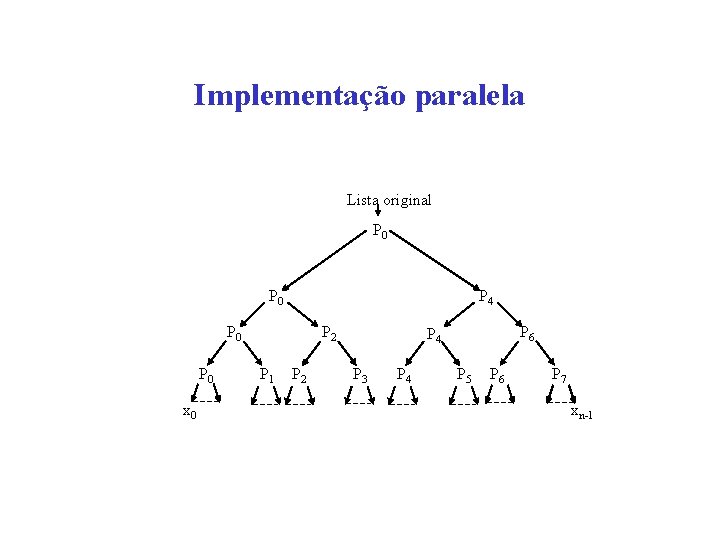
Implementação paralela Lista original P 0 P 4 P 0 x 0 P 2 P 1 P 2 P 6 P 4 P 3 P 4 P 5 P 6 P 7 xn-1

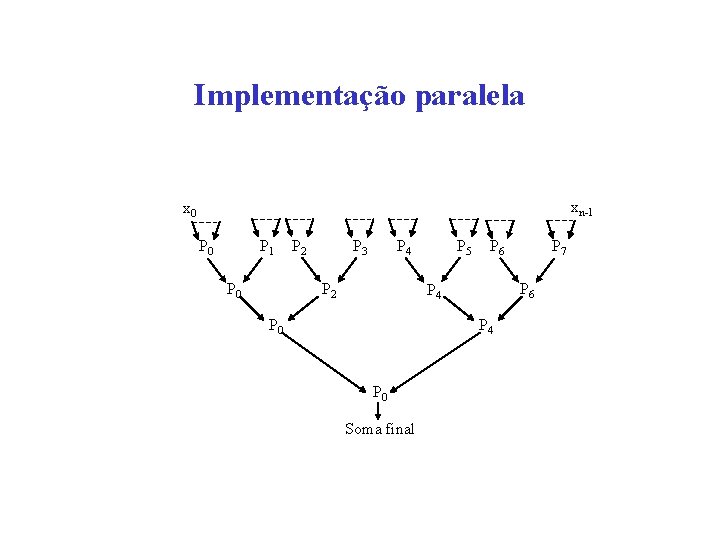
Implementação paralela xn-1 x 0 P 1 P 0 P 2 P 3 P 4 P 2 P 5 P 6 P 4 P 0 Soma final P 7

Código paralelo • Suponha que foram criados 8 processos estáticamente Processo P 0 divide(s 1, s 2); send(s 2, P 4); divide(s 1, s 2); send(s 2, P 2); divide(s 1, s 2); send(s 2, P 1); part_sum = *s 1; recv(&part_sum 1, P 1); part_sum=part_sum + part_sum 1; recv(&part_sum 1, P 2); part_sum=part_sum + part_sum 1; recv(&part_sum 1, P 4); part_sum=part_sum + part_sum 1;

Código paralelo Processo P 4 recv(s 1, P 0); divide(s 1, s 2); send(s 2, P 6); divide(s 1, s 2); send(s 2, P 5); part_sum = *s 1; recv(&part_sum 1, P 5); part_sum=part_sum + part_sum 1; recv(&part_sum 1, P 6); part_sum=part_sum + part_sum 1; send(&part_sum, P 0);

Análise de complexidade • Assuma que n é uma potência de 2 e tstartup não é incluído – Fase 1: Comunicação - Divisão – Fase 2: Combinação – Fase 3: Tempo total de comunicação – Computação – Tempo total

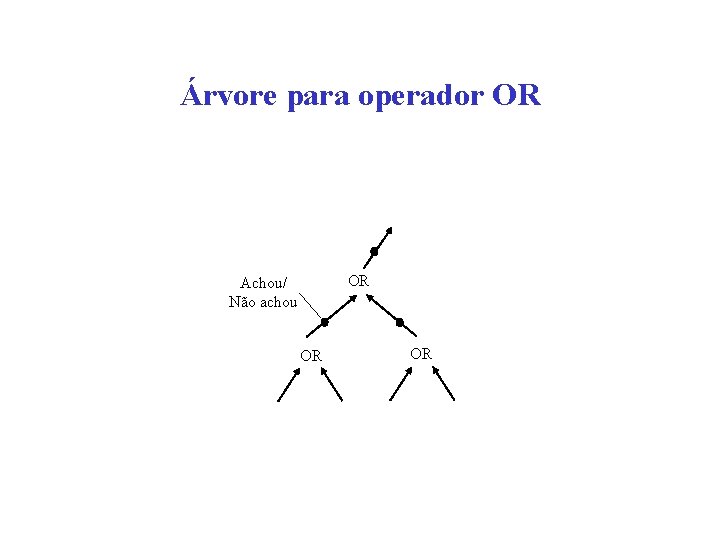
Árvore para operador OR OR Achou/ Não achou OR OR

Dividir e conquistar M-ário • As tarefas são divididas em mais de uma parte em cada estágio • Exemplo: Uma tarefa é quebrada em 4 partes. A definição recursiva poderia ser int add (int *s) { } if (number(s) <= 4) return (n 1 + n 2+n 3+n 4); else { divide (s, s 1, s 2, s 3, s 4); part_sum 1 = add(s 1); part_sum 2 = add(s 2); part_sum 3 = add(s 3); part_sum 4 = add(s 4); return(part_sum 1 + part_sum 2+part_sum 3 + part_sum 4); }

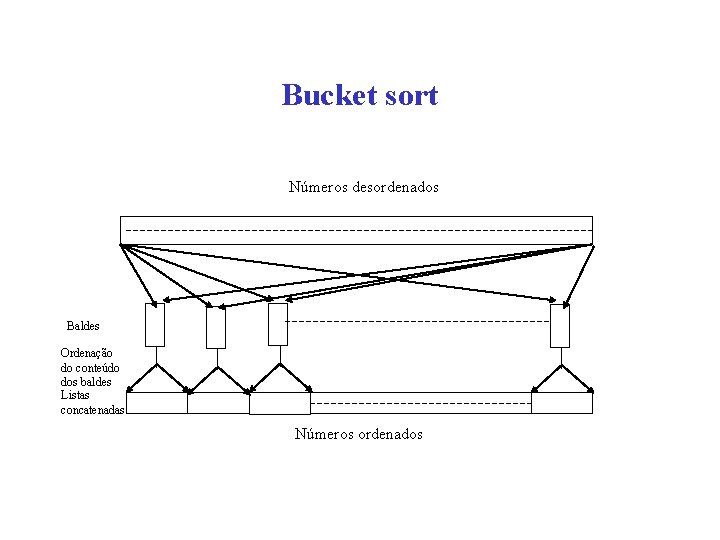
Exemplos utilizando divisão e conquista • Ordenação utilizando bucket sort – O intervalo de números é dividido em m regiões iguais, 0 até a/m-1, a/m até 2 a/m-1, 2 a/m até 3 a/m-1, … – Um balde ( bucket) é designado para armazenar os números que estão em uma determinada região – Os números são colocados nos baldes associados – Os números de cada balde serão ordenados através de um algoritmo de ordenação seqüencial – Funciona bem, se números estiverem distribuídos de forma uniforme em um intervalo conhecido 0 até a-1

Bucket sort Números desordenados Baldes Ordenação do conteúdo dos baldes Listas concatenadas Números ordenados

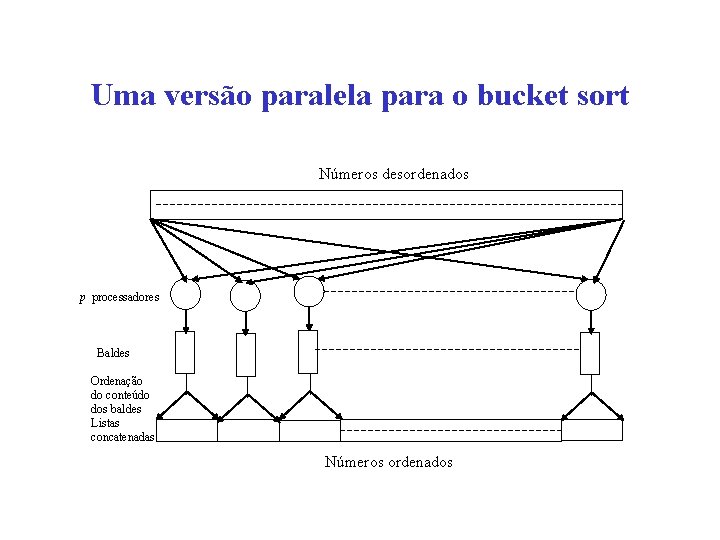
Análise de complexidade para o bucket sort • Tempo seqüencial • Tempo paralelo – Designando um processador para cada balde, teremos que o segundo termo da equação acima será reduzido para quando forem utilizados p processadores, onde p=m.

Uma versão paralela para o bucket sort Números desordenados p processadores Baldes Ordenação do conteúdo dos baldes Listas concatenadas Números ordenados

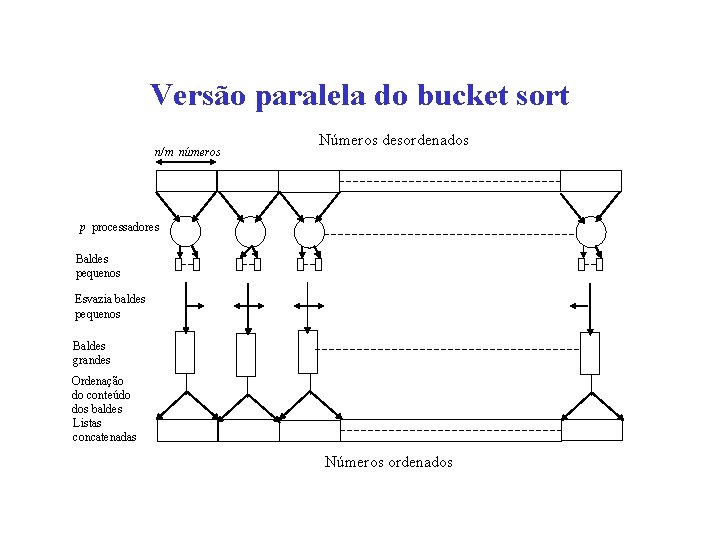
Maior paralelização • Particiona a seqüência em m regiões, uma para cada processador • Cada processador mantém p baldes pequenos e separa os números nas suas regiões nos seus próprios baldes menores • Esses baldes menores são esvaziados nos p baldes finais, que requer que cada processador envie um balde pequeno para cada um dos outros processadores (balde i para processador i)

Versão paralela do bucket sort n/m números Números desordenados p processadores Baldes pequenos Esvazia baldes pequenos Baldes grandes Ordenação do conteúdo dos baldes Listas concatenadas Números ordenados

Análise de complexidade – Fase 1: Computação e Comunicação - Particionando os números – Fase 2: Computação (ordenação nos baldes menores) – Fase 3: Comunicação (envio para os baldes maiores) – Computação (ordenação nos baldes maiores) – Tempo total

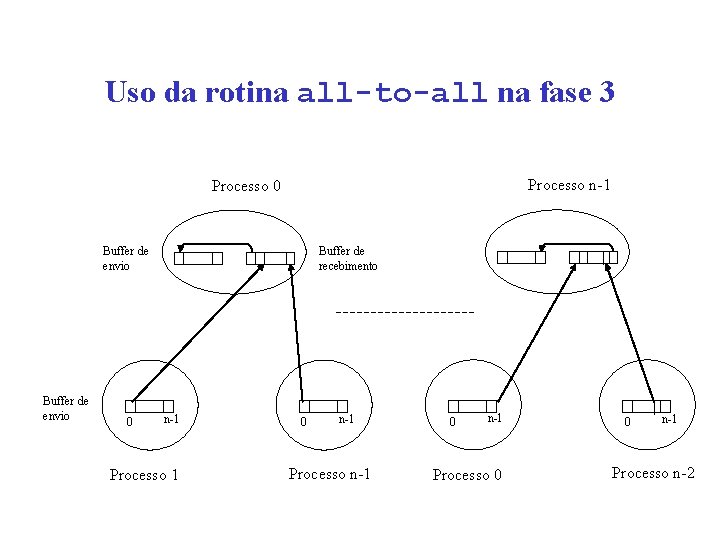
Uso da rotina all-to-all na fase 3 Processo n-1 Processo 0 Buffer de envio 0 Buffer de recebimento n-1 Processo 1 0 n-1 Processo n-1 0 n-1 Processo 0 0 n-1 Processo n-2

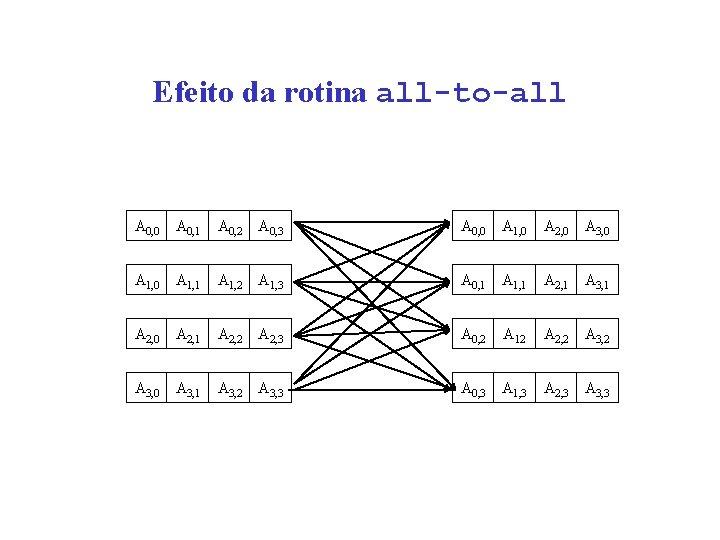
Efeito da rotina all-to-all A 0, 0 A 0, 1 A 0, 2 A 0, 3 A 0, 0 A 1, 0 A 2, 0 A 3, 0 A 1, 1 A 1, 2 A 1, 3 A 0, 1 A 1, 1 A 2, 1 A 3, 1 A 2, 0 A 2, 1 A 2, 2 A 2, 3 A 0, 2 A 12 A 2, 2 A 3, 0 A 3, 1 A 3, 2 A 3, 3 A 0, 3 A 1, 3 A 2, 3 A 3, 3

Integração numérica • Uma técnica geral de divisão e conquista consiste em dividir a região continuamente em partes e existe uma função de otimização que decide quando certas regiões estão suficientemente divididas • Exemplo: – Integração numérica: divide a área em partes separadas e cada uma delas pode ser calculada por um processo separado

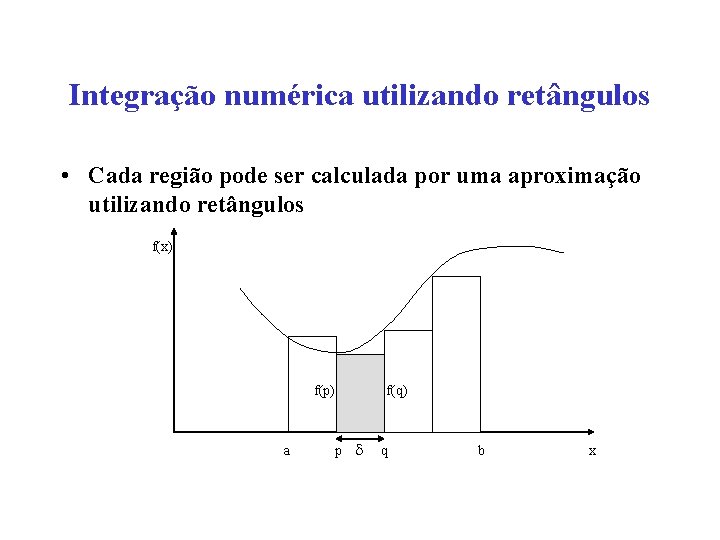
Integração numérica utilizando retângulos • Cada região pode ser calculada por uma aproximação utilizando retângulos f(x) f(p) a f(q) p q b x

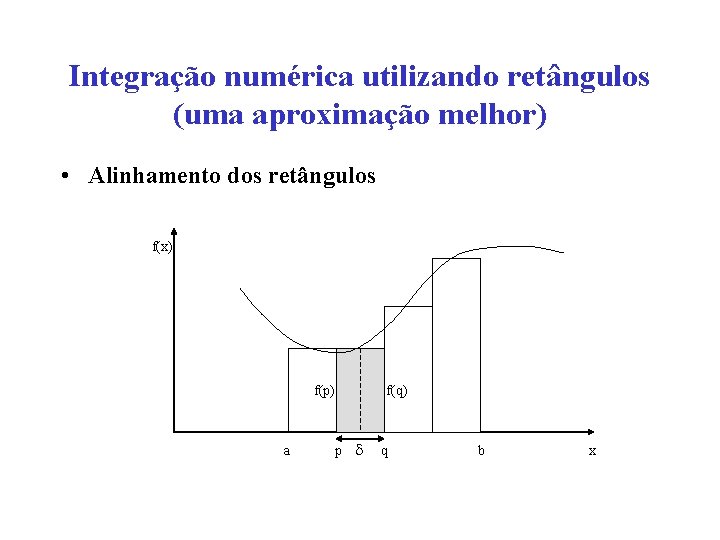
Integração numérica utilizando retângulos (uma aproximação melhor) • Alinhamento dos retângulos f(x) f(p) a f(q) p q b x

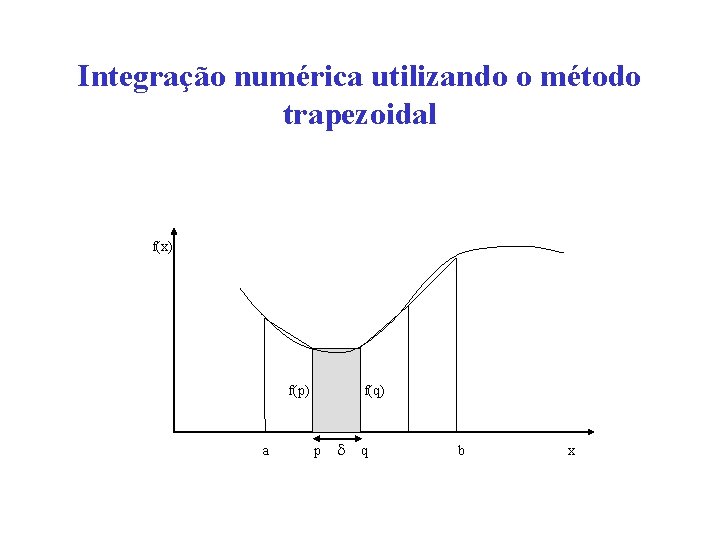
Integração numérica utilizando o método trapezoidal f(x) f(p) a f(q) p q b x

Designação estática • Pseudo código SPMD Processo Pi if (i == master) { printf (“Entre com o número de intervalos “); scanf (“%d”, &n); } bcast(&n, Pgroup); region = (b-a)/p; start=a + region * i; end = start + region; d=(b-a)/n; area=0. 0; for (x = start; x <end; x = x+d) area = area +f(x) + f(x+d); area=0. 5 * area * d; reduce_add(&integral, &area, Pgroup);

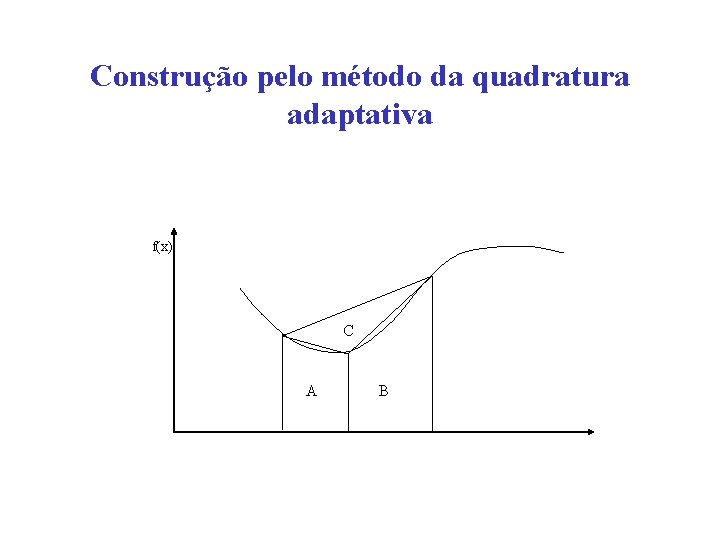
Método da quadratura adaptativa • Solução se adapta ao formato da curva • Exemplo: – Utilize 3 áreas A, B e C. A computação termina quando a área calculada para a maior das regiões entre A e B tiver um valor suficientemente próximo à soma das áreas para as outras regiões

Construção pelo método da quadratura adaptativa f(x) C A B

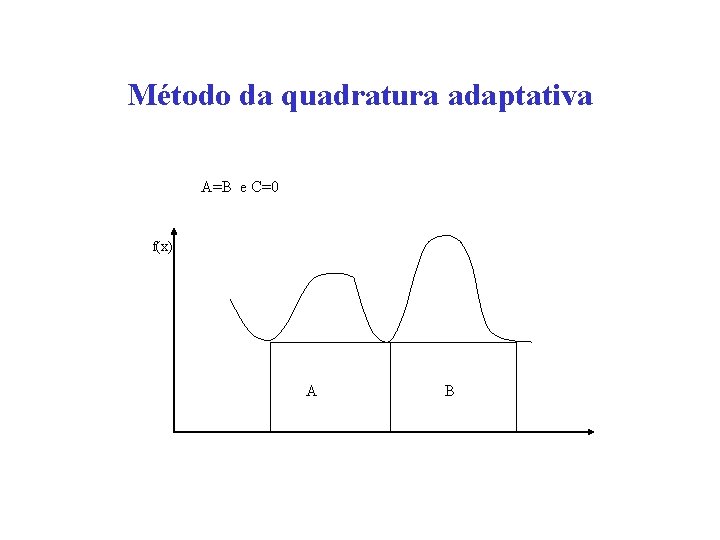
Método da quadratura adaptativa A=B e C=0 f(x) A B

Problema dos N-corpos • Encontrar as posições e movimentos de corpos no espaço que estão sujeitos a forças gravitacionais dos outros corpos segundo as leis de Newton • A força gravitacional entre dois corpos de massas ma e mb é dada por onde G é uma constante e r a distância entre os corpos • Submetido a uma força um corpo acelera segundo a segunda Lei de Newton: onde m é a massa do corpo, F a força a que ele está submetido e a a aceleração resultante

Problema dos N-corpos • Seja o intervalo de tempo t. Então para um corpo com massa m, a força é dada por • a nova velocidade por • e a mudança de posição • Depois que os corpos se movem para as novas posições, as forças mudam e o cálculo tem que ser repetido

Espaço tridimensional • Temos as coordenadas (x, y, z) e a distância entre os corpos em (xa, ya, za) e (xb, yb, zb) é dada por • e as forças são resolvidas nas 3 direções por

Código seqüencial para N-corpos for (t = 0; t , tmax; t++) { for (i = 0; i < N; i++) { F=Force_routine(i); v[i]new = v[i[ + F * dt/m; x[i]new = x[i] + v[i]new * dt; } for (i = 0; i < N; i++) { x[i] = x[i]new; v[i] = v[i]new; } }

Código paralelo para N-corpos • O algoritmo seqüencial tem complexidade O(n 2) para cada iteração pois cada um dos N corpos é influenciado pelos outros N-1 corpos • Não é possível utilizar o algoritmo seqüencial diretamente para os problemas mais interessantes onde N é grande • A complexidade pode ser reduzida observando-se que um grupo de corpos distantes pode ser aproximado com um único corpo distante com a massa total dos corpos do grupo e situado no centro de massa do grupo

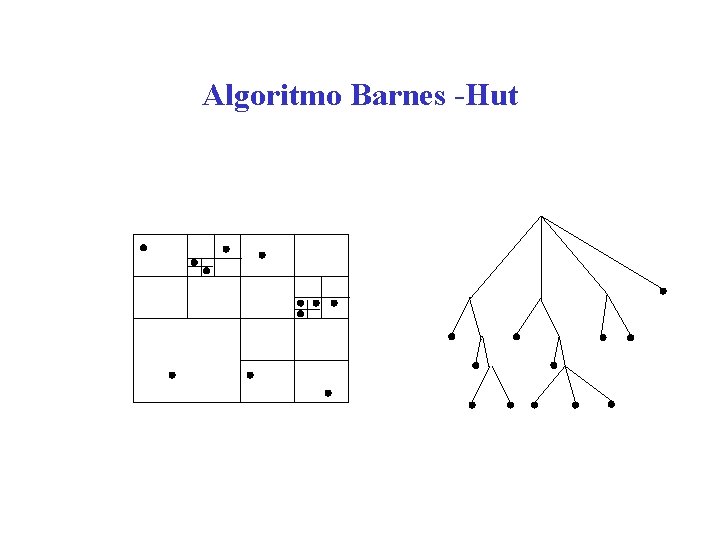
Algoritmo Barnes-Hut • Inicie com um espaço único no qual um cubo contém todos os corpos • Divida esse cubo em 8 subcubos • Se um subcubo não contém corpos, o subcubo é retirado da lista de subcubos a serem analisados • Se um subcubo contém mais de um corpo, ele é recursivamente dividido em subcubos, até que cada subcubo contenha apenas um corpo • Esse processo cria uma octtree, 8 arestas de cada nó • As folhas representam os subcubos com um corpo só • Em cada nó, armazenam-se a massa total e o centro de massa de cada subcubo

Algoritmo Barnes-Hut • A força de cada corpo pode ser obtida atravessando a árvore construída a partir da raíz, parando quando a aproximação de agrupamento pode ser usada, isto é, quando: • onde é uma constante tipicamente com valor 1. 0 ou menor • A complexidade para construção da árvore é O(nlogn), complexidade do método O(nlogn)

Algoritmo Barnes -Hut