Estimation of Porosity and Permeability from 4 DSeismic

Estimation of Porosity and Permeability from 4 D-Seismic and Production Data Using Principal Component Analysis M. Dadashpour, D. Echeverria Ciaurri, T. Mukerji, J. Kleppe, and M. Landrø Smart Fields Seminar Stanford University July 31, 2008 1

Outline • • The Norne Field The history matching problem Integrating production and seismic data The optimization problem Principal Component Analysis Results Conclusions 2

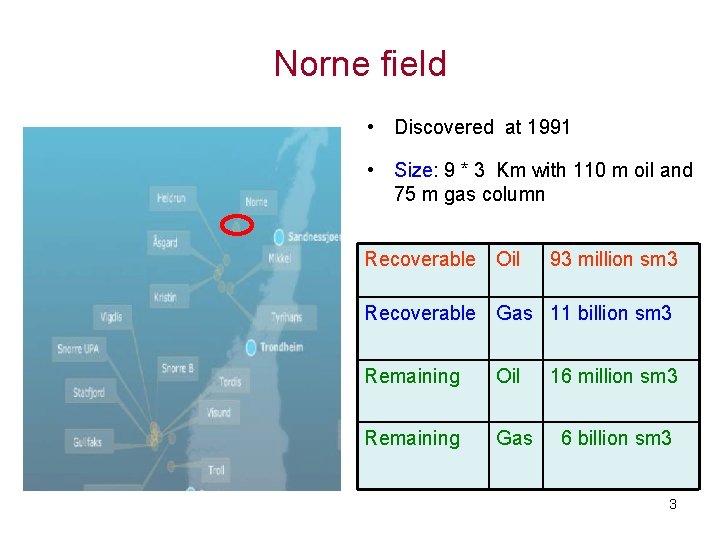
Norne field • Discovered at 1991 • Size: 9 * 3 Km with 110 m oil and 75 m gas column • Seismic Survey: Recoverable Oil 93 million sm 3 • Base: 1991 (Conventional) • 1 th: July 2001 Q-Marine survey Recoverable Gas 11 billion sm 3 • 2 th: August 2003 Q-Marine survey • 3 th: August 2004 Q-Marine Remaining Oil 16 million survey sm 3 • 4 th: August 2006 Q-Marine survey • 5 th: July 2008 Q-Marine survey Remaining Gas 6 billion sm 3 3

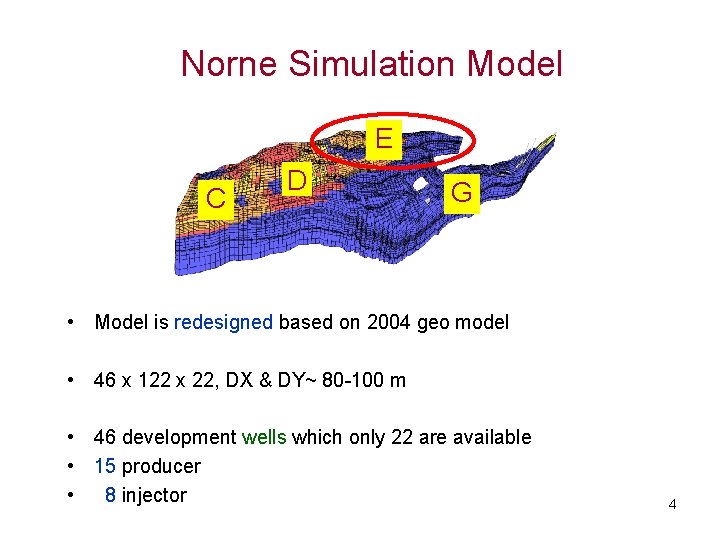
Norne Simulation Model E C D G • Model is redesigned based on 2004 geo model • 46 x 122 x 22, DX & DY~ 80 -100 m • 46 development wells which only 22 are available • 15 producer • 8 injector 4

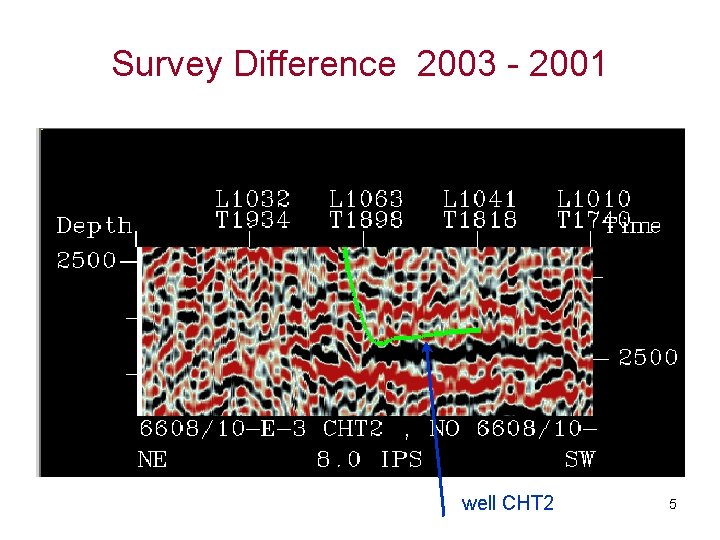
Survey Difference 2003 - 2001 well CHT 2 5

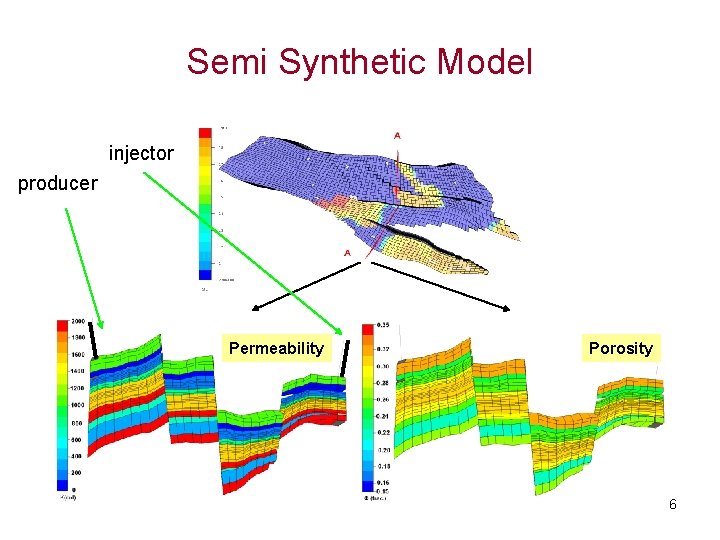
Semi Synthetic Model injector producer Permeability Porosity 6

Outline • • The Norne Field The history matching problem Integrating production and seismic data The optimization problem Principal Component Analysis Results Conclusions 7

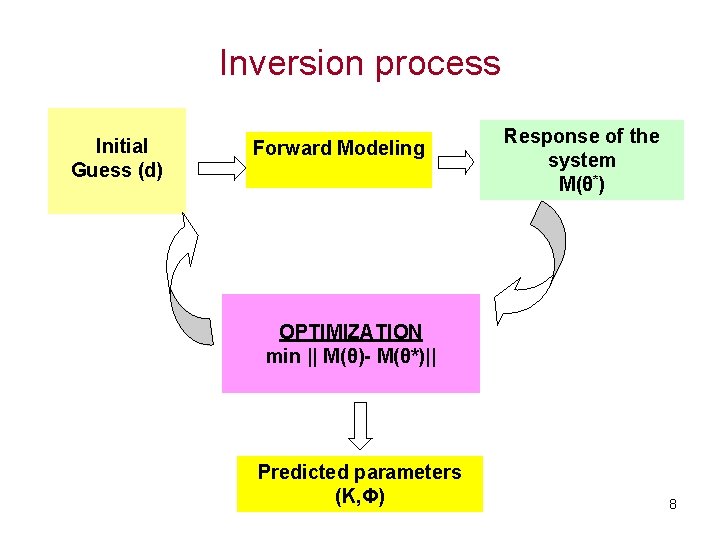
Inversion process Initial Guess (d) Forward Modeling Response of the system M(θ*) OPTIMIZATION min || M(θ)- M(θ*)|| Predicted parameters (K, Φ) 8

Outline • • The Norne Field The history matching problem Integrating production and seismic data The optimization problem Principal Component Analysis Results Conclusions 9

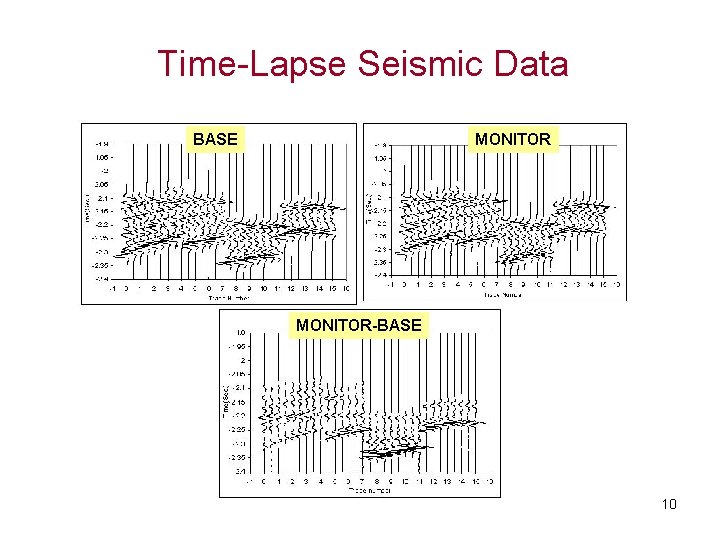
Time-Lapse Seismic Data BASE MONITOR-BASE 10

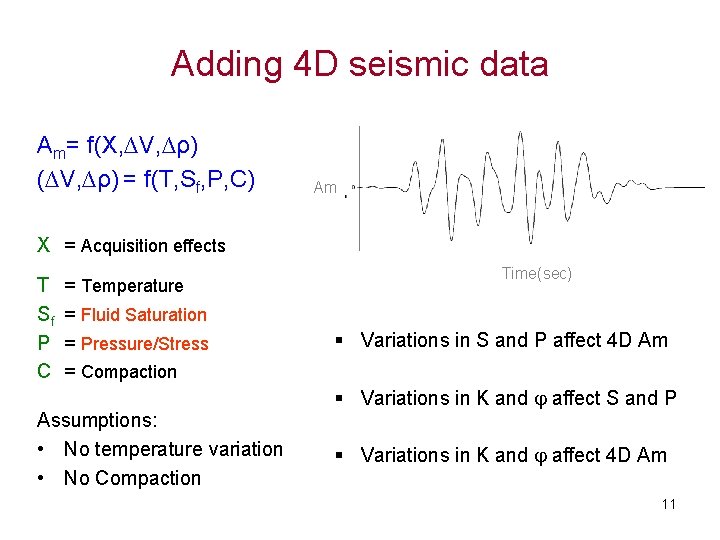
Adding 4 D seismic data Am= f(X, ∆V, ∆ρ) (∆V, ∆ρ) = f(T, Sf, P, C) Am X = Acquisition effects T Sf P C = Temperature = Fluid Saturation = Pressure/Stress = Compaction Time(sec) § Variations in S and P affect 4 D Am § Variations in K and affect S and P Assumptions: • No temperature variation • No Compaction § Variations in K and affect 4 D Am 11

Adding 4 D seismic data Real 4 D Seismic Processing Processed 4 D Seismic Real Production Data Sim Seismic Data Match Petro Elastic model Reservoir Properties Flow Simulation ΔS, ΔP 12

Forward Models Used Production § Fluid Flow Simulation (Eclipse 100) Seismic § Petro Elastic Model – Gassmann’s equation (Saturation) – Hertz Mindlin Model (Pressure) § Forward seismic Modeling (Matrix propagation techniques) 13

Outline • • The Norne Field The history matching problem Integrating production and seismic data The optimization problem Principal Component Analysis Results Conclusions 14

Objective Function Observed Data Production Seismic 15

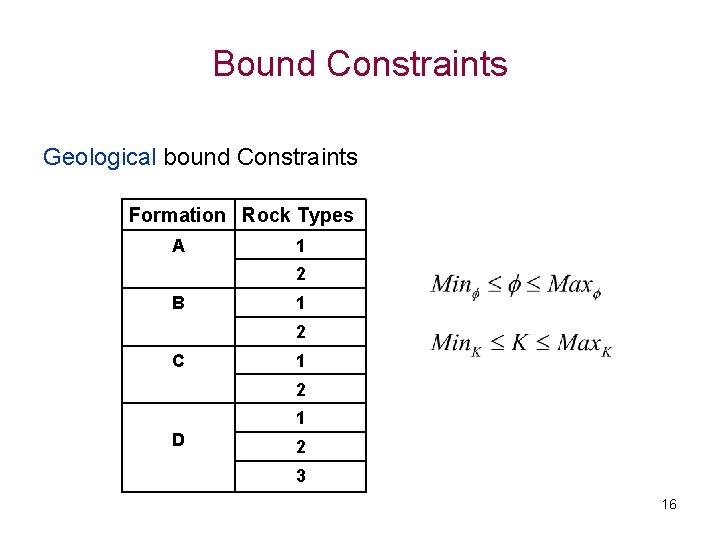
Bound Constraints Geological bound Constraints Formation Rock Types A 1 2 B 1 2 C 1 2 1 D 2 3 16

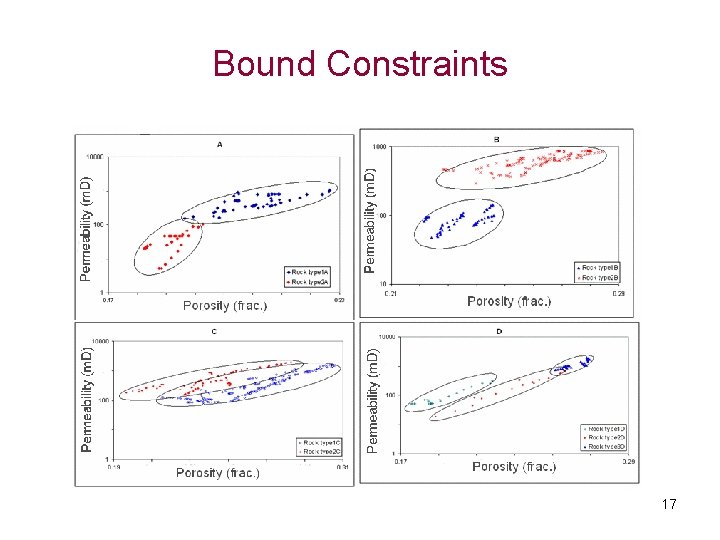
Bound Constraints 17

Four Optimization Strategies √ √ √ √ √ * production data is added after 15 iterations 18

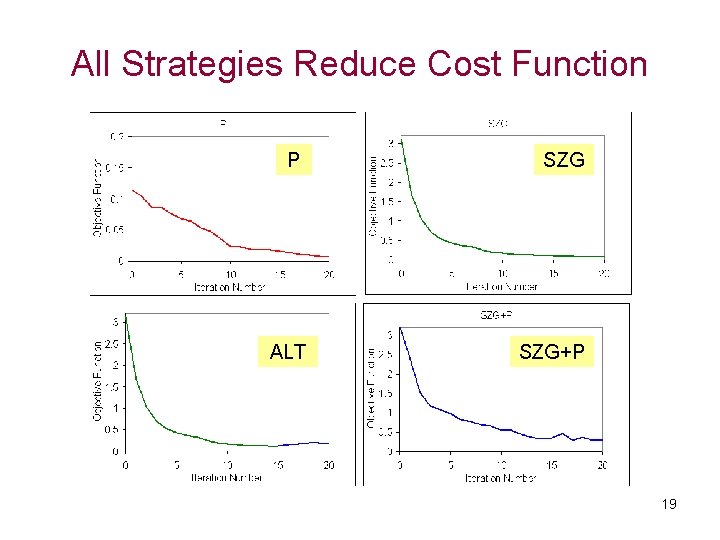
All Strategies Reduce Cost Function P SZG ALT SZG+P 19

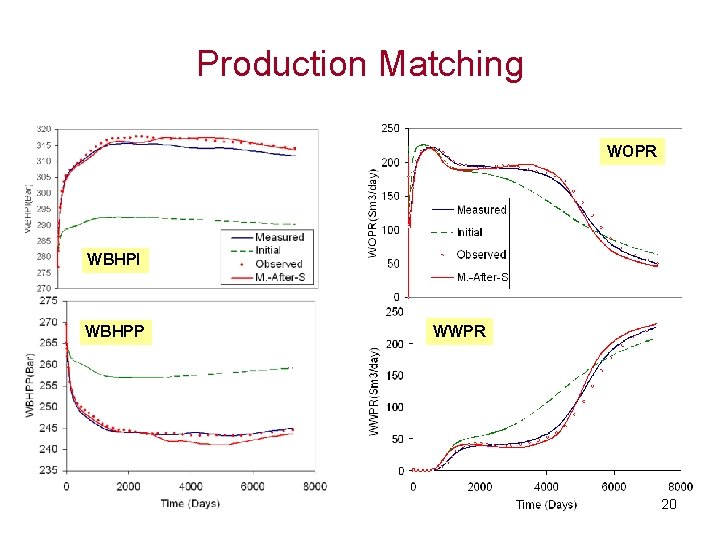
Production Matching WOPR WBHPI WBHPP WWPR 20

4 D Seismic Matching Zero Offset Amplitude Mismatch AVO Gradients Mismatch 121% 140% 20% 21

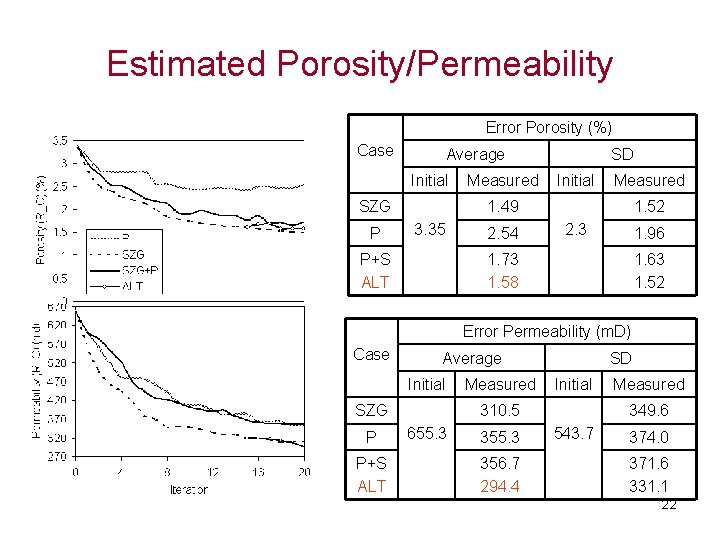
Estimated Porosity/Permeability Error Porosity (%) Case Average Initial SZG P Measured SD Initial Measured 1. 49 3. 35 P+S ALT 2. 54 1. 52 2. 3 1. 96 1. 73 1. 58 1. 63 1. 52 Error Permeability (m. D) Case Average Initial SZG P P+S ALT Measured SD Initial 310. 5 655. 3 356. 7 294. 4 Measured 349. 6 543. 7 374. 0 371. 6 331. 1 22

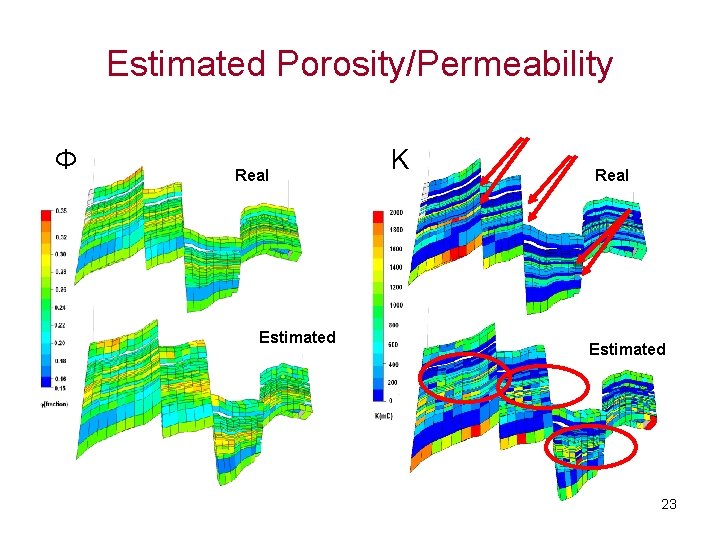
Estimated Porosity/Permeability Φ Real Estimated K Real Estimated 23

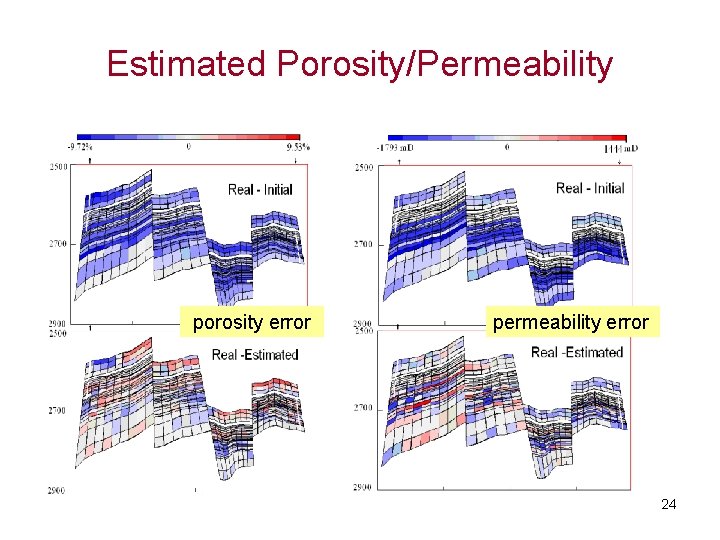
Estimated Porosity/Permeability porosity error permeability error 24

Outline • • The Norne Field The history matching problem Integrating production and seismic data The optimization problem Principal Component Analysis Results Conclusions 25

Motivation for PCA NOP Simulation time (sec) Optimization time (days) Semi Synthetic Model 1478 30 10. 0 Real Norne Model 2000 1200 556. 0 Semi Synthetic Model (PCA) 200 30 1. 5 Real Norne Model(PCA) 200 1200 55. 0 CPU-TIME=Number of forward Simulation x Number of Iterations § reduce CPU time § have a geologically acceptable estimate expected 26

Principal Component Analysis • Orthogonal linear transformation • Other names: – Karhunen-Loeve Transform (KLT) – Proper Orthogonal Decomposition (POD) – Hotelling Transform • Involves eigenvalue decomposition / singular value decomposition of a covariance matrix • Application: – reduces dimension in multidimensional data sets – Introduces naturally geologic constraints 27

Principal Component Analysis • Interpretation as data compression orthonormal with so that is maximized and from D. Echeverria Ciaurri et al. 2008 28

Porosity Realizations • Matrix Approach: when size of the problem is huge • Turning Ban: has artifacts and conditioning to local data is difficult • Fractals: conditioning to local data is difficult • Annealing: recommended for permeability • Sequential Gaussian Simulation 29

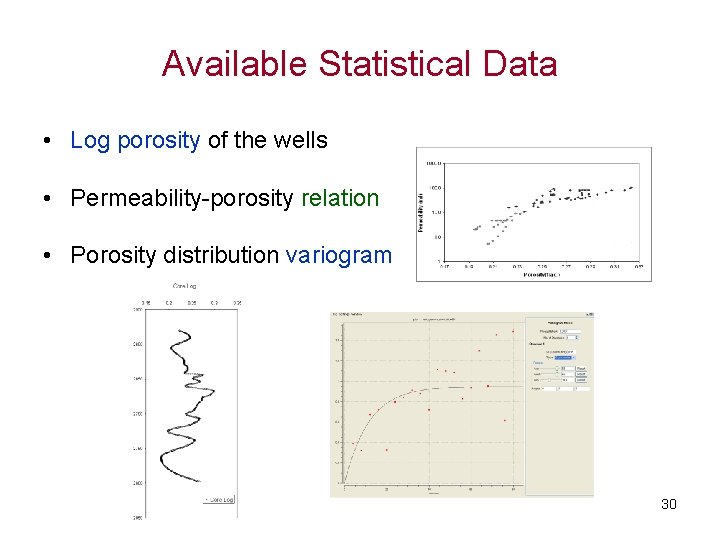
Available Statistical Data • Log porosity of the wells • Permeability-porosity relation • Porosity distribution variogram 30

Sequential Gaussian Simulation • All conditional distribution is Gaussian and the mean and variance is given by kriging. Procedure 1. 2. 3. 4. Transform data to normal scores Establish grid network and coordinate system Compute the variogram corresponding to available well data Simulate realization by ordinary kriging which is conditioned to – variogram – local well data – … 5. Back transform all values 31

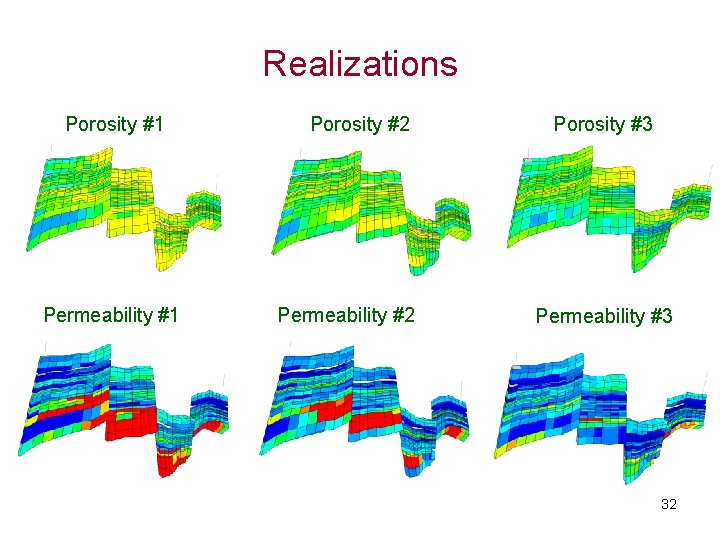
Realizations Porosity #1 Permeability #1 Porosity #2 Permeability #2 Porosity #3 Permeability #3 32

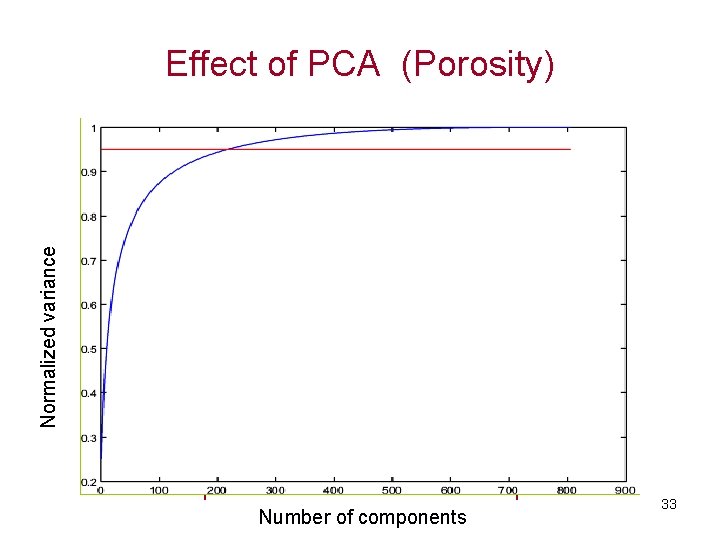
Normalized variance Effect of PCA (Porosity) Original 200 components 100 components 50 components Number of components 33

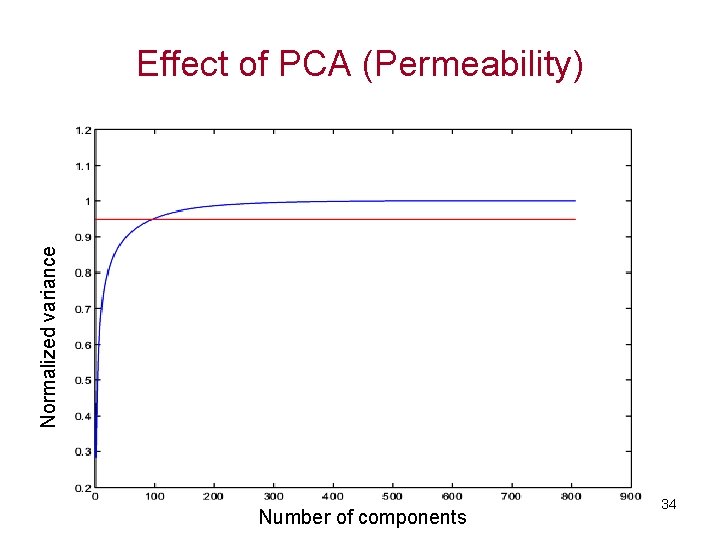
Normalized variance Effect of PCA (Permeability) Original 200 components 100 components 50 components Number of components 34

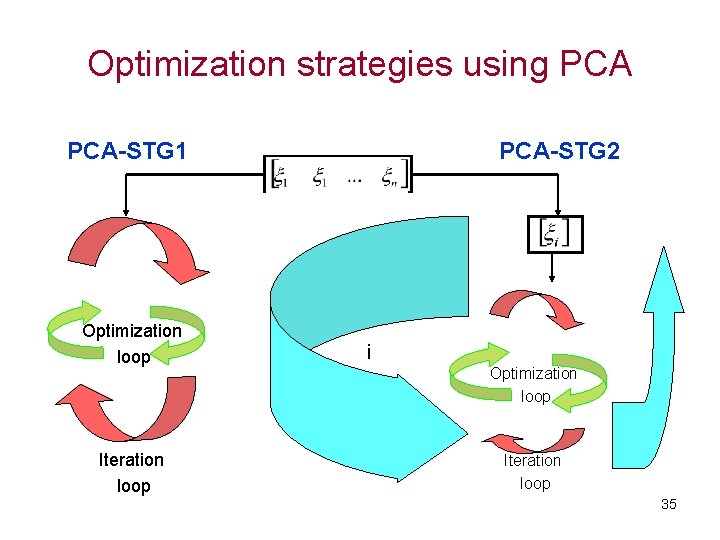
Optimization strategies using PCA-STG 1 Optimization loop Iteration loop PCA-STG 2 i Optimization loop Iteration loop 35

Outline • • The Norne Field The history matching problem Integrating production and seismic data The optimization problem Principal Component Analysis Results Conclusions 36

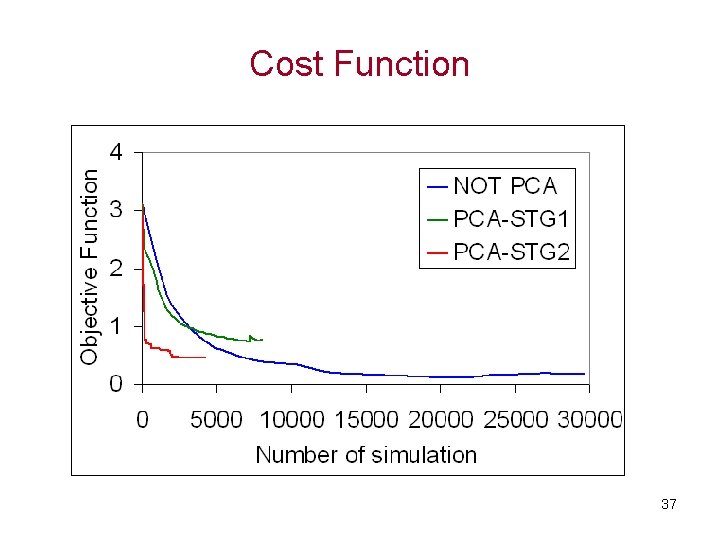
Cost Function 37

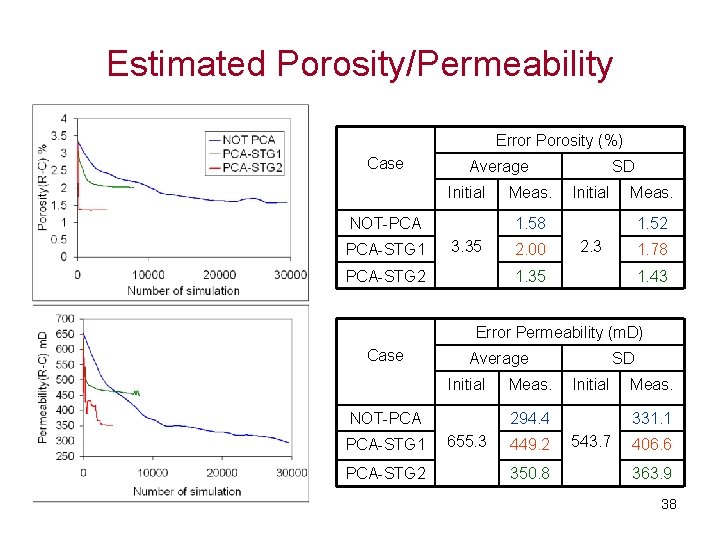
Estimated Porosity/Permeability Error Porosity (%) Case Average Initial NOT-PCA PCA-STG 1 Meas. SD Initial Meas. 1. 58 3. 35 PCA-STG 2 2. 00 1. 52 2. 3 1. 78 1. 35 1. 43 Error Permeability (m. D) Case Average Initial NOT-PCA PCA-STG 1 PCA-STG 2 Meas. SD Initial 294. 4 655. 3 449. 2 350. 8 Meas. 331. 1 543. 7 406. 6 363. 9 38

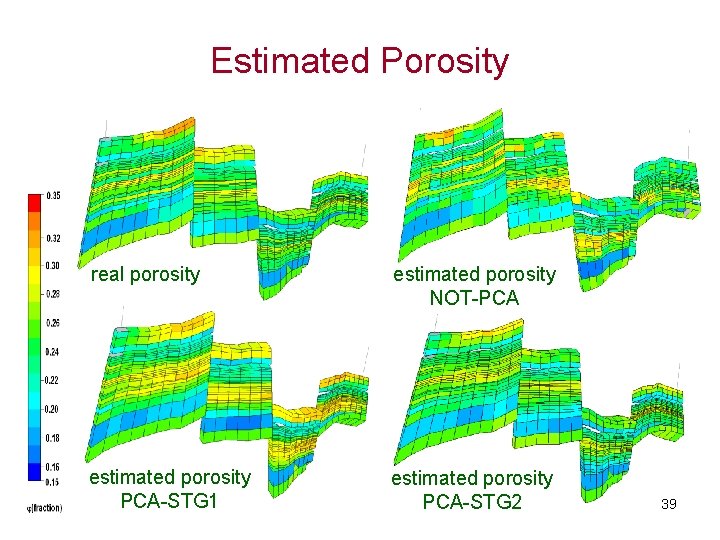
Estimated Porosity real porosity estimated porosity NOT-PCA estimated porosity PCA-STG 1 estimated porosity PCA-STG 2 39

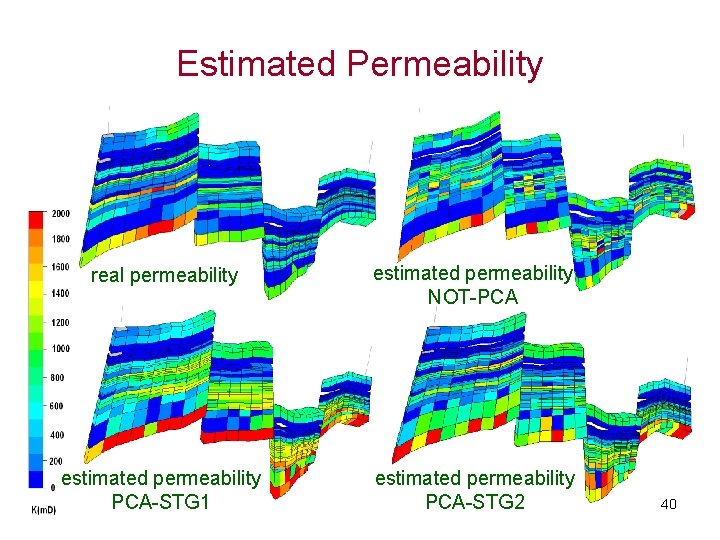
Estimated Permeability real permeability estimated permeability NOT-PCA estimated permeability PCA-STG 1 estimated permeability PCA-STG 2 40

Outline • • The Norne Field The history matching problem Integrating production and seismic data The optimization problem Principal Component Analysis Results Conclusions 41

Conclusions • Adding 4 D seismic to production data yields a better history match • If geologic constraints are not considered, the matched solutions might not be geologically realistic • If numerical gradients are used in the history matching, the computational load can be prohibitive for practical applications 42

Conclusions • By Principal Component Analysis (PCA) we can speed up the gradient-based optimization considerably and at the same time take into account geologic constraints • The good results obtained with this PCA-based technique in a semi synthetic case from the Norne field encourage to apply to the history matching of the complete field 43

Future Work • Apply PCA-based optimization to the complete field • Use distributed computing in gradient approximation • Test alternative optimization algorithms • Study efficient methods (adjoints) for gradient computation • Extension of PCA to Kernel PCA 44

Acknowledgements NTNU NFR Stanford • STATOIL for permission to use the reservoir model • Schlumberger-Geo. Quest for the use of the Eclipse simulator. • Alexey Stovas (NTNU) for the seismic forward modeling • Jan Ivar Jensen (NTNU) For assistance 45

Thank You! 46

Estimation of Porosity and Permeability from 4 D-Seismic and Production Data Using Principal Component Analysis M. Dadashpour, D. Echeverria Ciaurri, T. Mukerji, J. Kleppe, and M. Landrø Smart Fields Seminar Stanford University July 31, 2008 47