Estimation of mortality rates General diagram of the




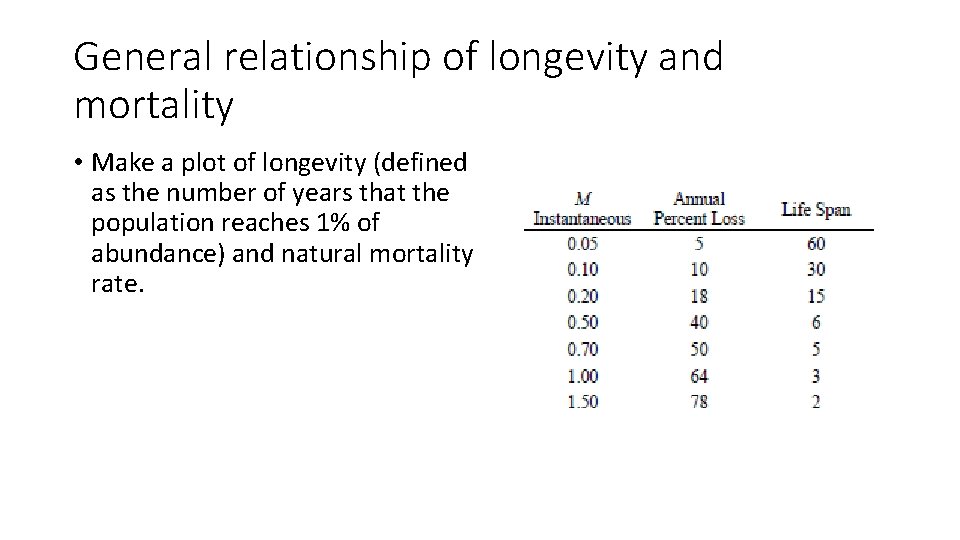







- Slides: 25

Estimation of mortality rates

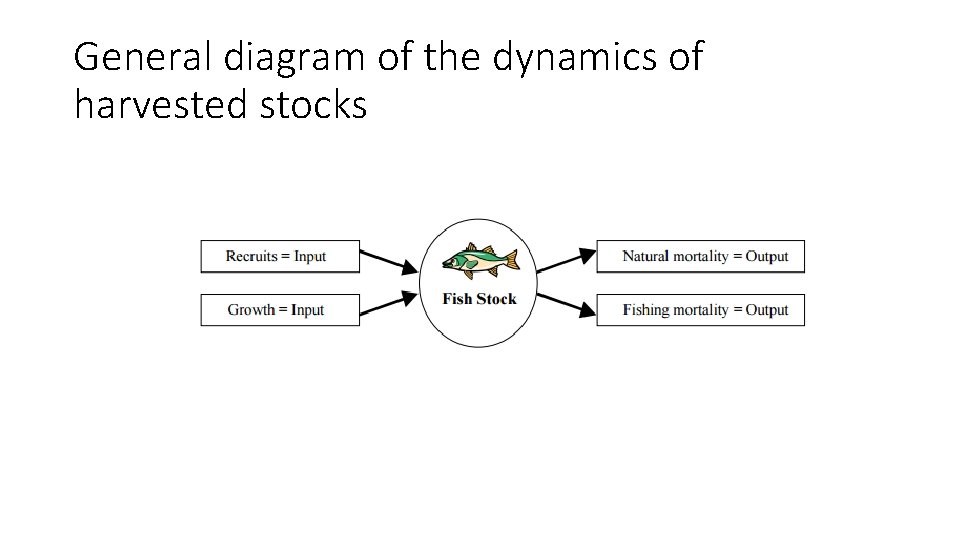
General diagram of the dynamics of harvested stocks

Mortality represents loss of individuals •

Mortality represents the loss •

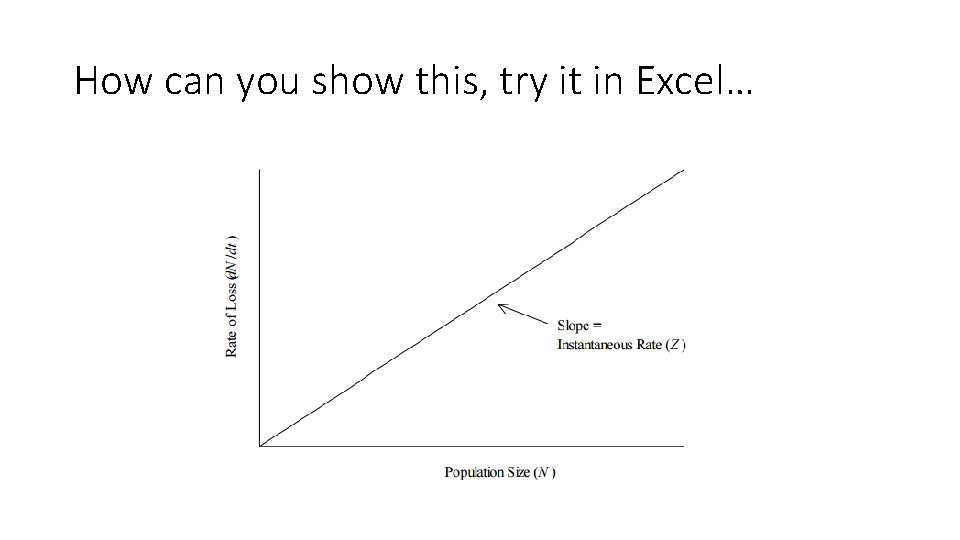
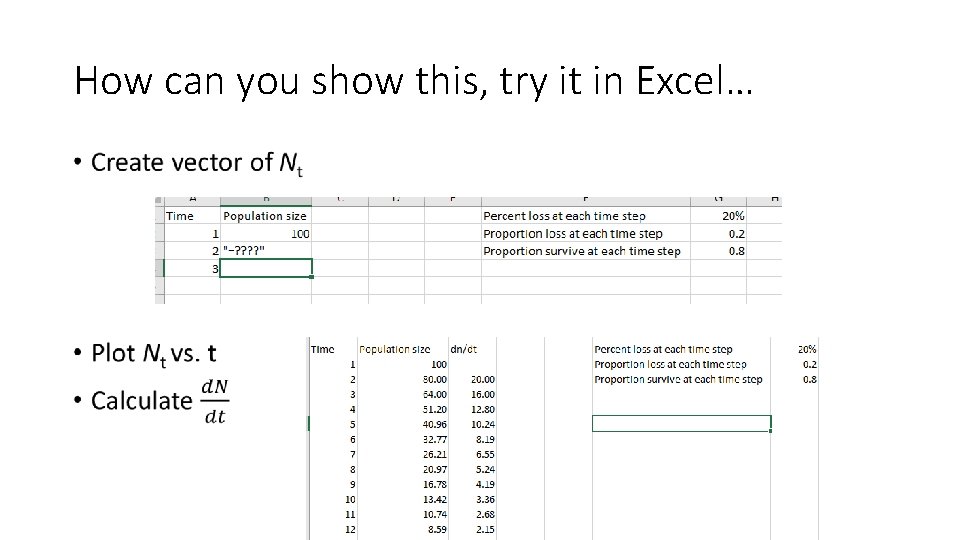
How can you show this, try it in Excel…

How can you show this, try it in Excel… •

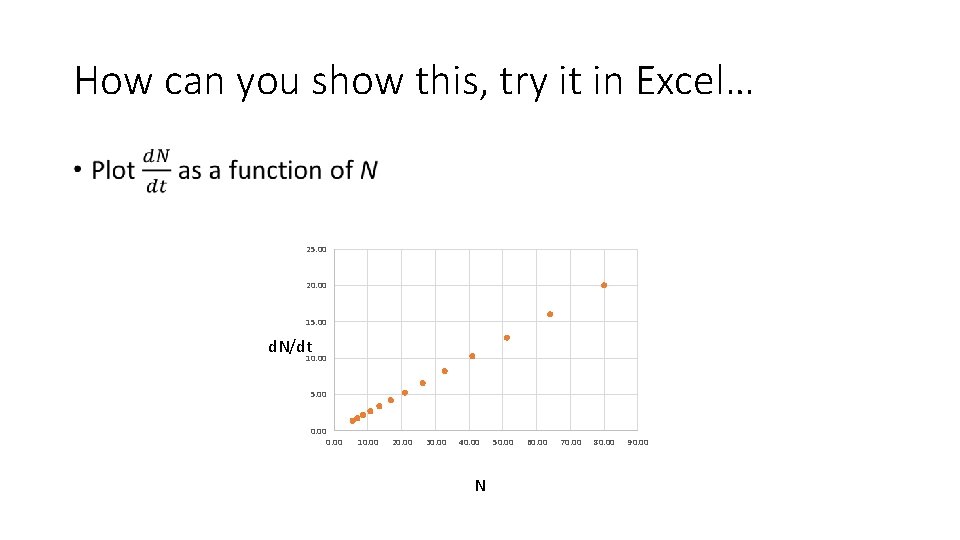
How can you show this, try it in Excel… • 25. 00 20. 00 15. 00 d. N/dt 10. 00 5. 00 0. 00 10. 00 20. 00 30. 00 40. 00 N 50. 00 60. 00 70. 00 80. 00 90. 00

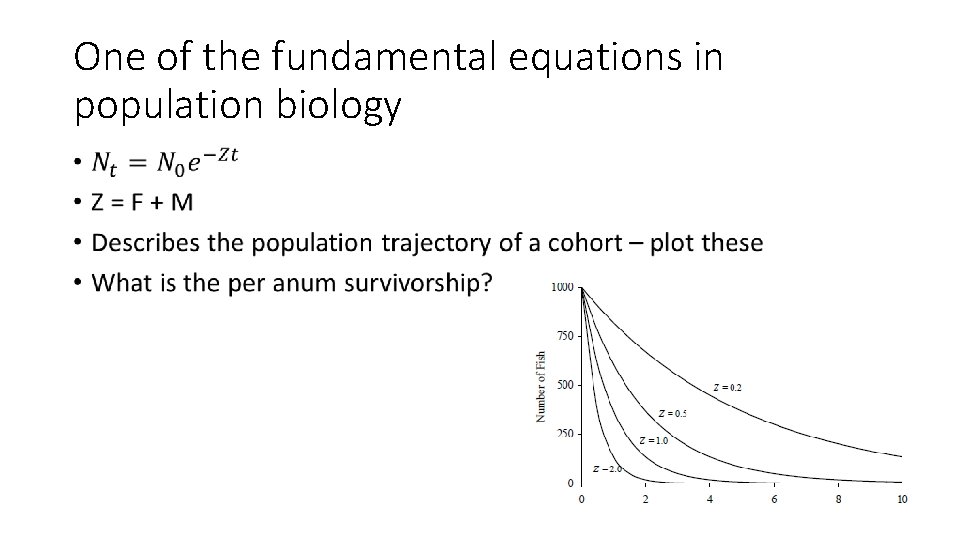
One of the fundamental equations in population biology •

Why instantaneous rates? • 1. What is the size of a cohort after three years that loses 34% of its population per annum. • Calculate this using proportions and instantaneous mortality rates. • 2. What is the size of a cohort after 14 years that loses 9% of the population every year for 13 years and 12% of the population at the terminal year? • 3. What is the size of a cohort in year three, that has a constant mortality rate, given that it starts with N = 500 and has N = 132 after five years.

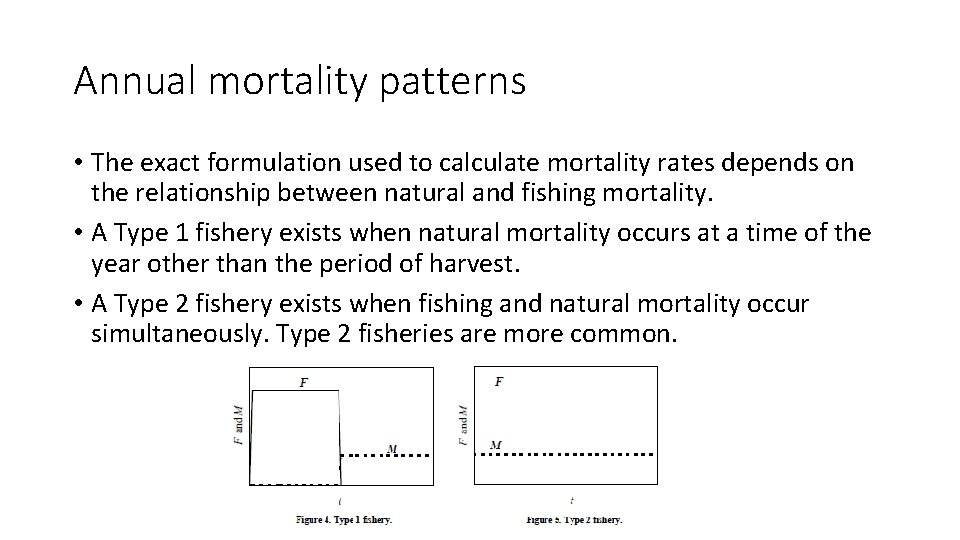
Annual mortality patterns • The exact formulation used to calculate mortality rates depends on the relationship between natural and fishing mortality. • A Type 1 fishery exists when natural mortality occurs at a time of the year other than the period of harvest. • A Type 2 fishery exists when fishing and natural mortality occur simultaneously. Type 2 fisheries are more common.
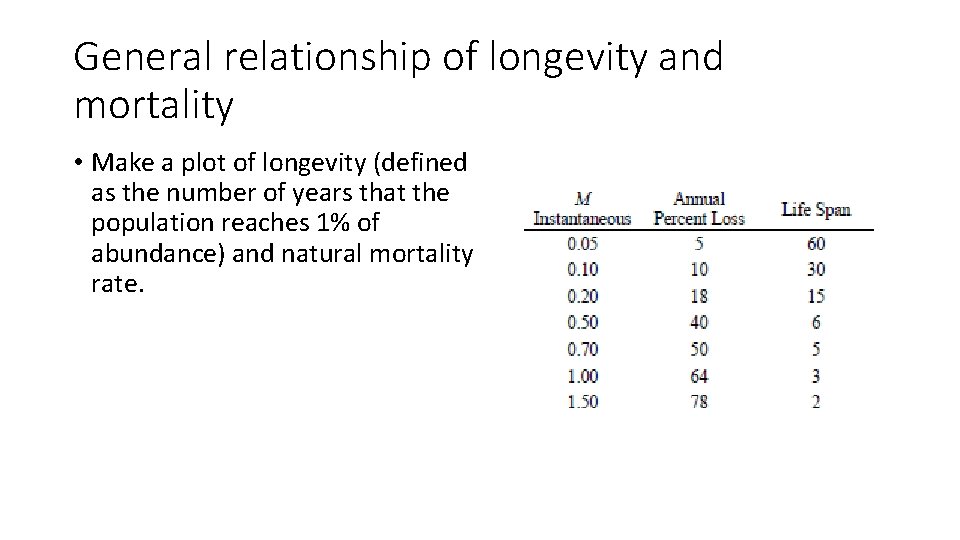
General relationship of longevity and mortality • Make a plot of longevity (defined as the number of years that the population reaches 1% of abundance) and natural mortality rate.

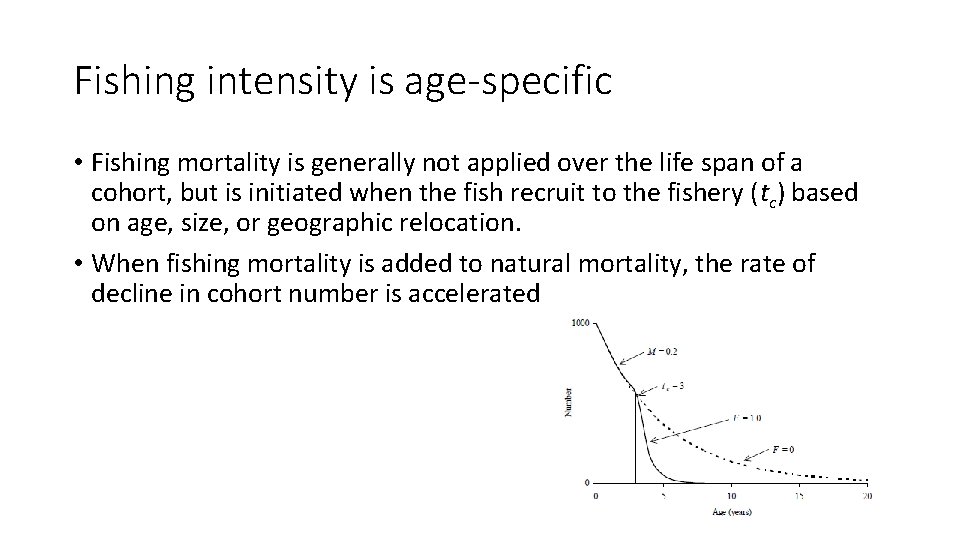
Fishing intensity is age-specific • Fishing mortality is generally not applied over the life span of a cohort, but is initiated when the fish recruit to the fishery (tc) based on age, size, or geographic relocation. • When fishing mortality is added to natural mortality, the rate of decline in cohort number is accelerated

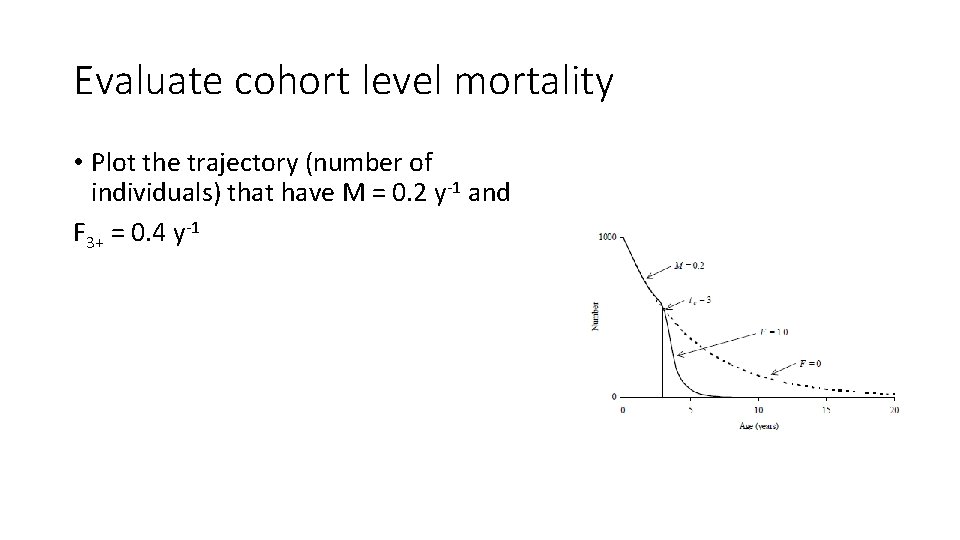
Evaluate cohort level mortality • Plot the trajectory (number of individuals) that have M = 0. 2 y-1 and F 3+ = 0. 4 y-1

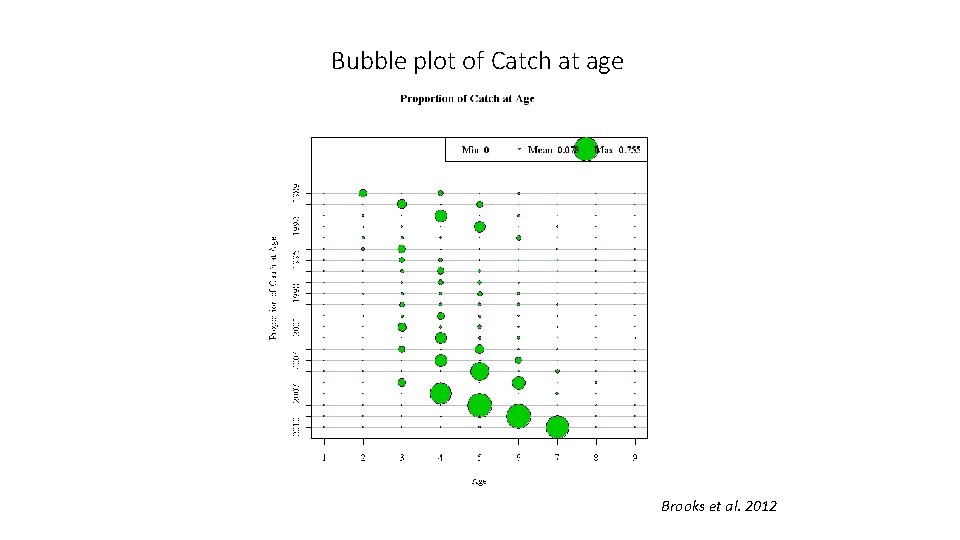
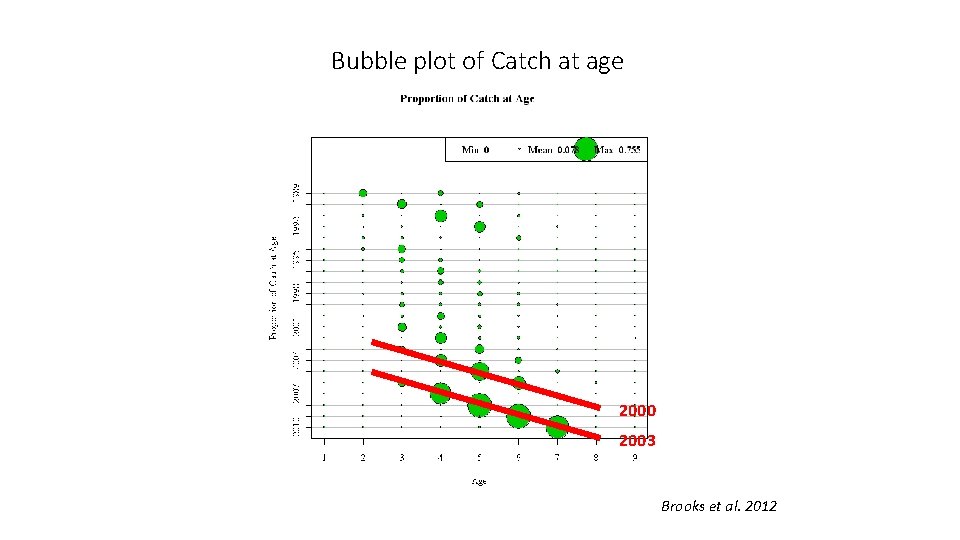
Mortality rate estimation • 1. Catch curves • Given age structured catch, can we infer what the mortality rates that determine the pattern are? • We know that the abundance of a cohort is determined by mortality… • The age structure of a population is the total of many cohorts • Use catch curve because we cannot just “follow” cohorts

Bubble plot of Catch at age Brooks et al. 2012

Bubble plot of Catch at age 2000 2003 Brooks et al. 2012

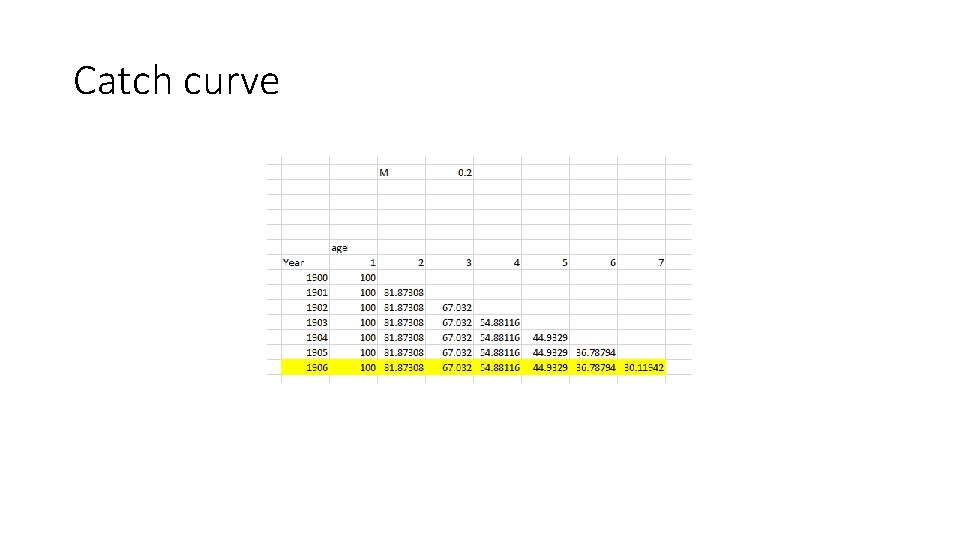
Catch curve

Catch curve

Catch curve

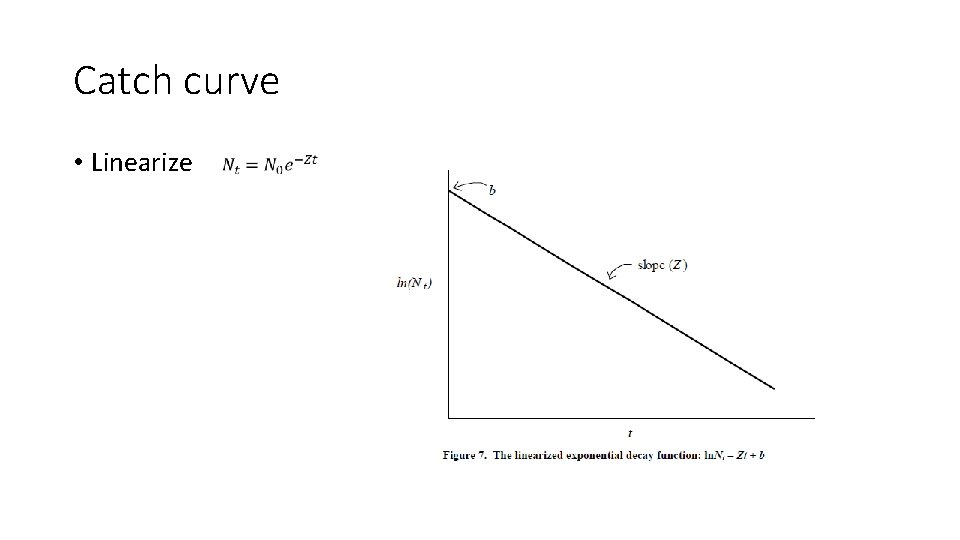
Catch curve • Linearize

Assumptions: • The survival rate is uniform with age, over the range of age-groups in question. • Since the survival rate is the complement of total mortality rate, and total mortality is composed of fishing and natural mortality, this will usually mean that each of these, individually, is uniform. • There has been no change in mortality rate with time. • The sample is taken randomly from the age-groups involved. • The age-groups in question were equal in numbers at the time each was being recruited to the fishery (constant recruitment).

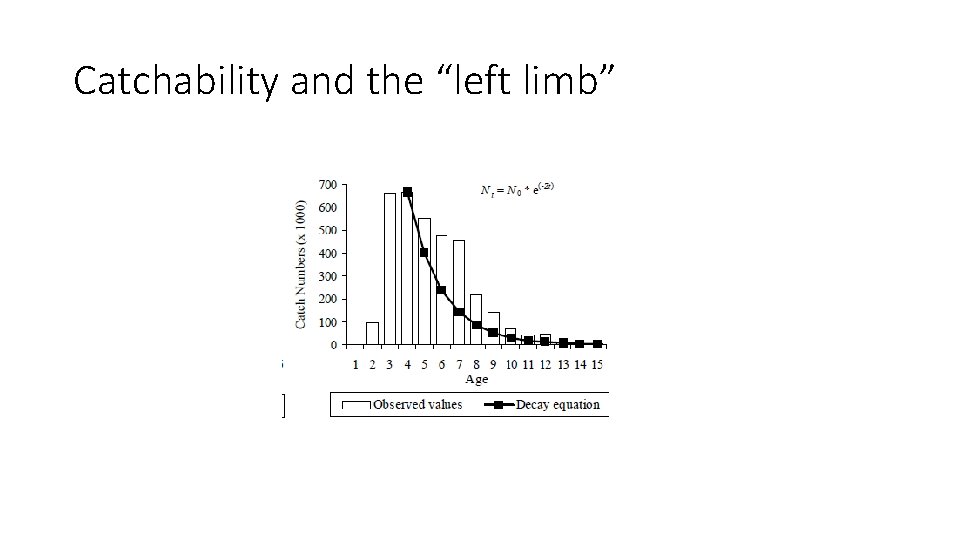
Assumptions: • The most common application of the catch curve is estimating mortality on a cohort from researchsurvey data. • If we collect a random sample using a trawl from a fish stock at a fixed time t, the mean catch at age per tow from one year to another can be used to estimate total mortality. • The sample is characterized by its catchability which can be defined as the “catch capacity of the gear per one unit of effort. ”

Catchability and the “left limb”

Thorson and Prager “better catch curves” • Thorson, James T. , and Prager, Michael H. 2011. Better catch curves: Incorporating age-specific natural mortality and logistic selectivity. Transactions of the American Fisheries Society. 140(2), 356 -366.

Empirical Estimates • Hoenig: