Estimation and Confidence Intervals Types of Estimators Point

Estimation and Confidence Intervals

Types of Estimators • Point Estimate üA single-valued estimate. üA single element chosen from a sampling distribution. üConveys little information about the actual value of the population parameter, about the accuracy of the estimate. • Confidence Interval or Interval Estimate üAn interval or range of values believed to include the unknown population parameter. üAssociated with the interval is a measure of the confidence we have that the interval does indeed contain the parameter of interest.

Confidence Interval or Interval Estimate A confidence interval or interval estimate is a range or interval of numbers believed to include an unknown population parameter. Associated with the interval is a measure of the confidence we have that the interval does indeed contain the parameter of interest. • A confidence interval or interval estimate has two components: üA range or interval of values üAn associated level of confidence

Confidence Interval for When Is Known • If the population distribution is normal, the sampling distribution of the mean is normal. If the sample is sufficiently large, regardless of the shape of the population distribution, the sampling distribution is normal (Central Limit Theorem). Standard Normal Distribution: 95% Interval 0. 4 0. 3 f(z) l 0. 2 0. 1 0. 0 -4 -3 -2 -1 0 z 1 2 3 4

Confidence Interval for when is Known (Continued)

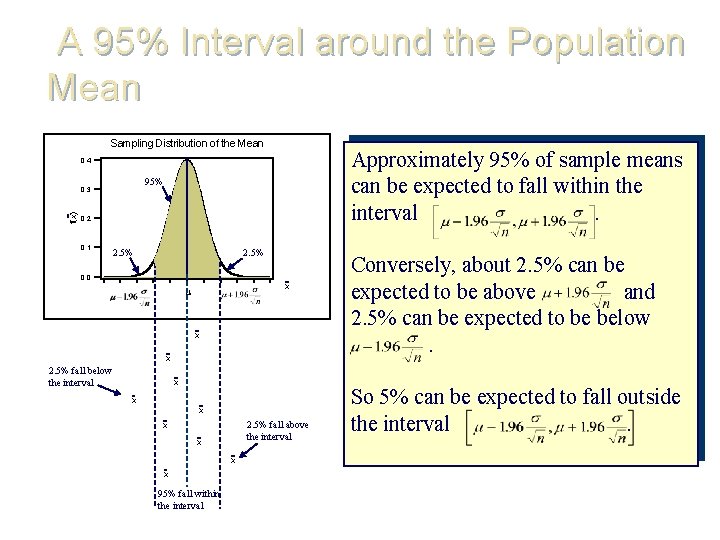
A 95% Interval around the Population Mean Sampling Distribution of the Mean Approximately 95% of sample means can be expected to fall within the interval. 0. 4 95% f(x) 0. 3 0. 2 0. 1 2. 5% 0. 0 x x x 2. 5% fall below the interval x x x 2. 5% fall above the interval x x 95% fall within the interval Conversely, about 2. 5% can be expected to be above and 2. 5% can be expected to be below. So 5% can be expected to fall outside the interval.

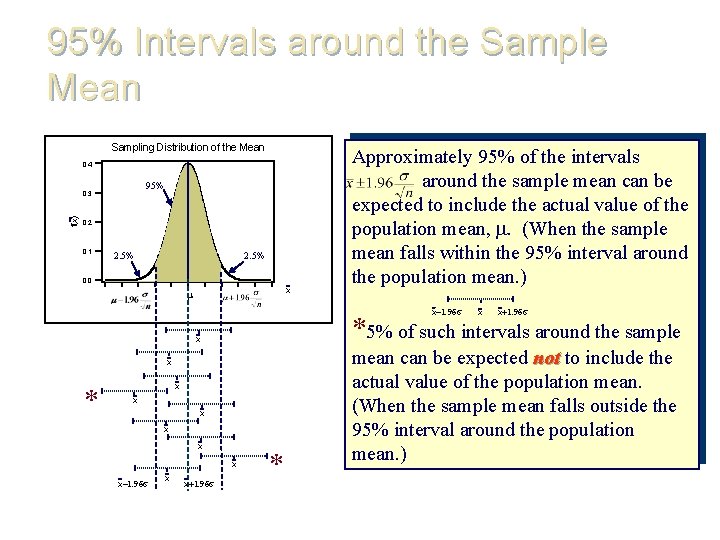
95% Intervals around the Sample Mean Sampling Distribution of the Mean 0. 4 95% f(x) 0. 3 0. 2 0. 1 2. 5% 0. 0 x Approximately 95% of the intervals around the sample mean can be expected to include the actual value of the population mean, . (When the sample mean falls within the 95% interval around the population mean. ) x x x x x x *5% of such intervals around the sample x * mean can be expected not to include the actual value of the population mean. (When the sample mean falls outside the 95% interval around the population mean. )

The 95% Confidence Interval for A 95% confidence interval for when is known and sampling is done from a normal population, or a large sample is used: The quantity sampling error. is often called the margin of error or the For example, if: n = 25 = 20 = 122 A 95% confidence interval:

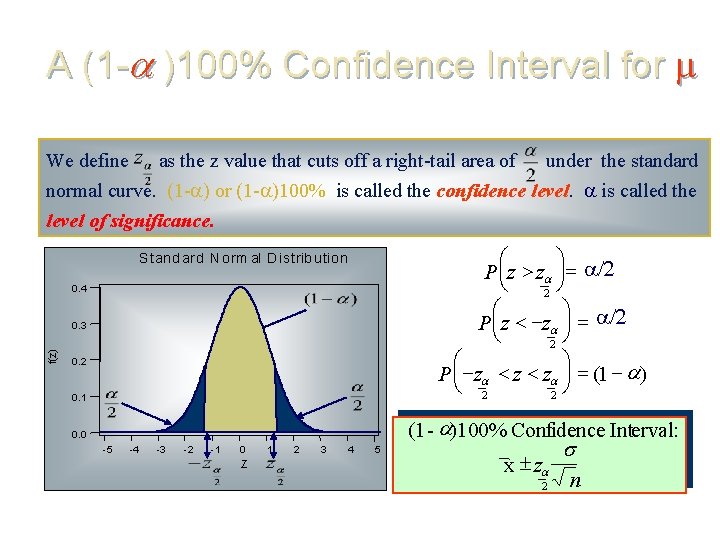
A (1 - )100% Confidence Interval for We define as the z value that cuts off a right-tail area of under the standard normal curve. (1 - ) or (1 - )100% is called the confidence level. is called the level of significance. 0. 1 æ ö P çz > z ÷ = /2 è ø 2 æ ö P çz < z ÷ = /2 è ø 2 æ ö < < P ç z z z ÷ = (1 ) è 2 ø 2 0. 0 (1 - )100% Confidence Interval: S tand ard Norm al Distrib ution 0. 4 f(z) 0. 3 0. 2 -5 -4 -3 -2 -1 0 Z 1 2 3 4 5 x ± z 2 s n

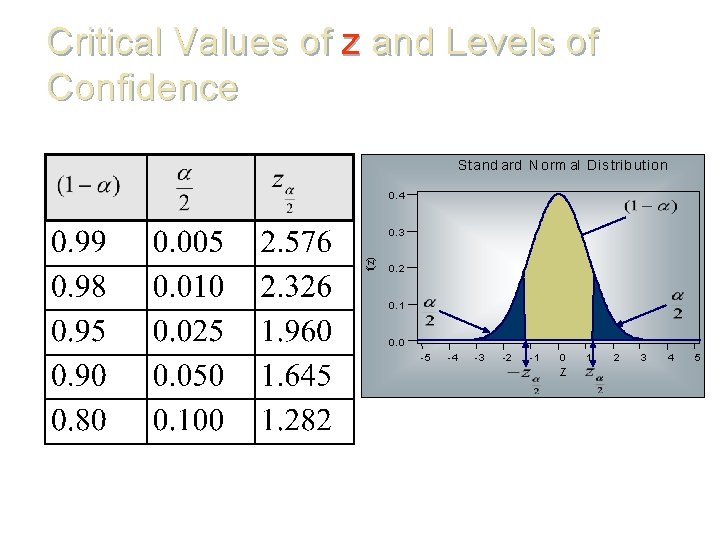
Critical Values of z and Levels of Confidence S tand ard N o rm al Distrib utio n 0. 4 f(z) 0. 3 0. 2 0. 1 0. 0 -5 -4 -3 -2 -1 0 Z 1 2 3 4 5

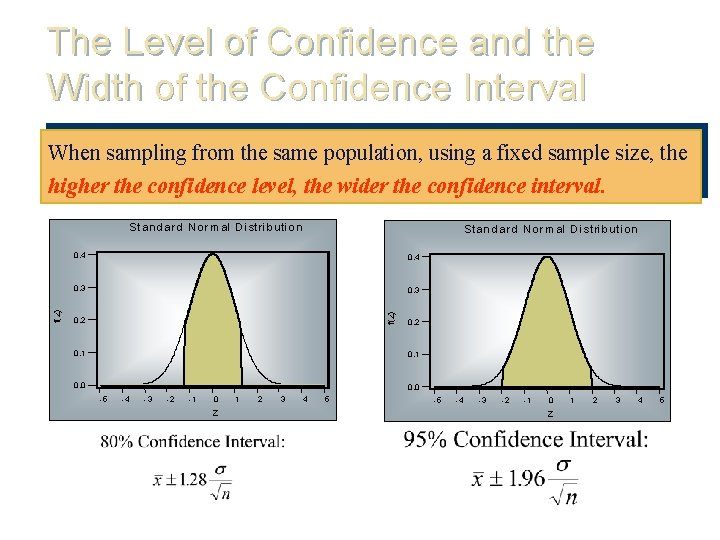
The Level of Confidence and the Width of the Confidence Interval When sampling from the same population, using a fixed sample size, the higher the confidence level, the wider the confidence interval. St an d ar d N or m al Di s tri b uti o n 0. 4 0. 3 f(z) St an d ar d N o r m al Di s tri b uti o n 0. 2 0. 1 0. 0 -5 -4 -3 -2 -1 0 Z 1 2 3 4 5

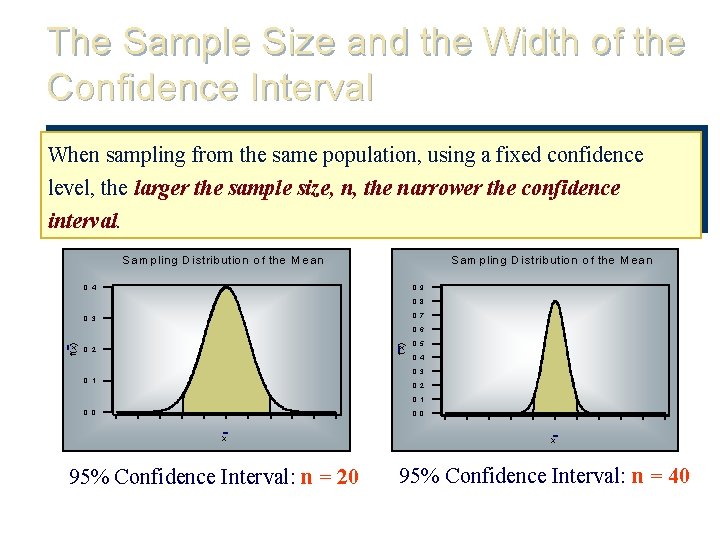
The Sample Size and the Width of the Confidence Interval When sampling from the same population, using a fixed confidence level, the larger the sample size, n, the narrower the confidence interval. S a m p lin g D is trib utio n o f th e M e an 0. 4 0. 9 0. 8 0. 7 0. 3 f(x) 0. 6 0. 2 0. 5 0. 4 0. 3 0. 1 0. 2 0. 1 0. 0 x 95% Confidence Interval: n = 20 x 95% Confidence Interval: n = 40

Point Estimates and Confidence Intervals for a Mean – σ Known EXAMPLE The American Management Association wishes to have information on the mean income of middle managers in the retail industry. A random sample of 256 managers reveals a sample mean of $45, 420. The standard deviation of this population is $2, 050. The association would like answers to the following questions: 1. 2. The width of the interval is determined by the level of confidence and the size of the standard error of the mean. The standard error is affected by two values: Standard deviation Number of observations in the sample 1. What is the population mean? In this case, we do not know. We do know the sample mean is $45, 420. Hence, our best estimate of the unknown population value is the corresponding sample statistic. 2. What is a reasonable range of values for the population mean? (Use 95% confidence level) The confidence limit are $45, 169 and $45, 671 The ±$251 is referred to as the margin of error 3. What do these results mean? If we select many samples of 256 managers, and for each sample we compute the mean and then construct a 95 percent confidence interval, we could expect about 95 percent of these confidence intervals to contain the population mean.

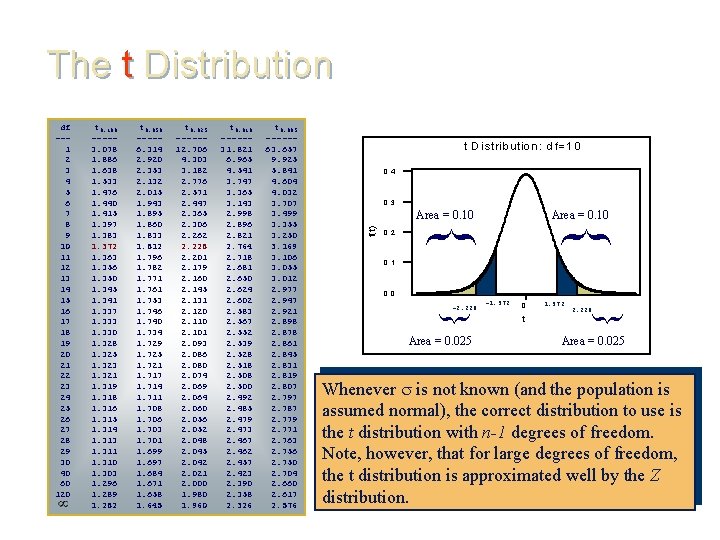
Confidence Interval or Interval Estimate for When Is Unknown - The t Distribution If the population standard deviation, , is not known, replace with the sample standard deviation, s. If the population is normal, the resulting statistic: has a t distribution with (n - 1) degrees of freedom. • • The t is a family of bell-shaped and symmetric distributions, one for each number of degree of freedom. The expected value of t is 0. The t is flatter and has fatter tails than does the standard normal. The t distribution approaches a standard normal as the number of degrees of freedom increases Standard normal t, df = 20 t, df = 10

Confidence Intervals for when is Unknown- The t Distribution A (1 - )100% confidence interval for when is not known (assuming a normally distributed population): where is the value of the t distribution with n-1 degrees of freedom that cuts off a tail area of to its right.

The t Distribution t 0. 005 -----63. 657 9. 925 5. 841 4. 604 4. 032 3. 707 3. 499 3. 355 3. 250 3. 169 3. 106 3. 055 3. 012 2. 977 2. 947 2. 921 2. 898 2. 878 2. 861 2. 845 2. 831 2. 819 2. 807 2. 797 2. 787 2. 779 2. 771 2. 763 2. 756 2. 750 2. 704 2. 660 2. 617 2. 576 t D is trib utio n: d f = 1 0 0. 4 0. 3 Area = 0. 10 0. 2 Area = 0. 10 } t 0. 010 -----31. 821 6. 965 4. 541 3. 747 3. 365 3. 143 2. 998 2. 896 2. 821 2. 764 2. 718 2. 681 2. 650 2. 624 2. 602 2. 583 2. 567 2. 552 2. 539 2. 528 2. 518 2. 500 2. 492 2. 485 2. 479 2. 473 2. 467 2. 462 2. 457 2. 423 2. 390 2. 358 2. 326 } t 0. 025 -----12. 706 4. 303 3. 182 2. 776 2. 571 2. 447 2. 365 2. 306 2. 262 2. 228 2. 201 2. 179 2. 160 2. 145 2. 131 2. 120 2. 110 2. 101 2. 093 2. 086 2. 080 2. 074 2. 069 2. 064 2. 060 2. 056 2. 052 2. 048 2. 045 2. 042 2. 021 2. 000 1. 980 1. 960 f(t) t 0. 050 ----6. 314 2. 920 2. 353 2. 132 2. 015 1. 943 1. 895 1. 860 1. 833 1. 812 1. 796 1. 782 1. 771 1. 761 1. 753 1. 746 1. 740 1. 734 1. 729 1. 725 1. 721 1. 717 1. 714 1. 711 1. 708 1. 706 1. 703 1. 701 1. 699 1. 697 1. 684 1. 671 1. 658 1. 645 0. 1 0. 0 -2. 228 Area = 0. 025 -1. 372 0 t 1. 372 2. 228 } t 0. 100 ----3. 078 1. 886 1. 638 1. 533 1. 476 1. 440 1. 415 1. 397 1. 383 1. 372 1. 363 1. 356 1. 350 1. 345 1. 341 1. 337 1. 333 1. 330 1. 328 1. 325 1. 323 1. 321 1. 319 1. 318 1. 316 1. 315 1. 314 1. 313 1. 311 1. 310 1. 303 1. 296 1. 289 1. 282 } df --1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 40 60 120 Area = 0. 025 Whenever is not known (and the population is assumed normal), the correct distribution to use is the t distribution with n-1 degrees of freedom. Note, however, that for large degrees of freedom, the t distribution is approximated well by the Z distribution.

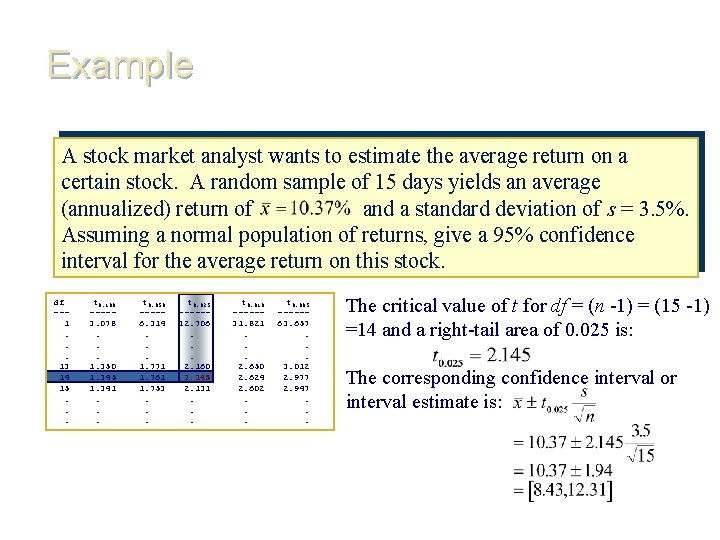
Example A stock market analyst wants to estimate the average return on a certain stock. A random sample of 15 days yields an average (annualized) return of and a standard deviation of s = 3. 5%. Assuming a normal population of returns, give a 95% confidence interval for the average return on this stock. df --1. . . 13 14 15. . . t 0. 100 ----3. 078. . . 1. 350 1. 345 1. 341. . . t 0. 050 ----6. 314. . . 1. 771 1. 761 1. 753. . . t 0. 025 -----12. 706. . . 2. 160 2. 145 2. 131. . . t 0. 010 -----31. 821. . . 2. 650 2. 624 2. 602. . . t 0. 005 -----63. 657. . . 3. 012 2. 977 2. 947. . . The critical value of t for df = (n -1) = (15 -1) =14 and a right-tail area of 0. 025 is: The corresponding confidence interval or interval estimate is:

Confidence Interval for the Mean – Example using the t-distribution EXAMPLE A tire manufacturer wishes to investigate the tread life of its tires. A sample of 10 tires driven 50, 000 miles revealed a sample mean of 0. 32 inch of tread remaining with a standard deviation of 0. 09 inch. Construct a 95 percent confidence interval for the population mean. Would it be reasonable for the manufacturer to conclude that after 50, 000 miles the population mean amount of tread remaining is 0. 30 inches?

Large Sample Confidence Intervals for the Population Mean df --1. . . 120 t 0. 100 ----3. 078. . . 1. 289 1. 282 t 0. 050 ----6. 314. . . 1. 658 1. 645 t 0. 025 -----12. 706. . . 1. 980 1. 960 t 0. 010 -----31. 821. . . 2. 358 2. 326 t 0. 005 -----63. 657. . . 2. 617 2. 576 Whenever is not known (and the population is assumed normal), the correct distribution to use is the t distribution with n-1 degrees of freedom. Note, however, that for large degrees of freedom, the t distribution is approximated well by the Z distribution. Large Sample : Sample size > 30

Large Sample Confidence Intervals for the Population Mean Example : An economist wants to estimate the average amount in checking accounts at banks in a given region. A random sample of 100 accounts gives x-bar = $357. 60 and s = $140. 00. Give a 95% confidence interval for , the average amount in any checking account at a bank in the given region.

Large-Sample Confidence Intervals for the Population Proportion, p

Large-Sample Confidence Intervals for the Population Proportion, p

Large-Sample Confidence Interval for the Population Proportion, p A marketing research firm wants to estimate the share that foreign companies have in the American market for certain products. A random sample of 100 consumers is obtained, and it is found that 34 people in the sample are users of foreign-made products; the rest are users of domestic products. Give a 95% confidence interval for the share of foreign products in this market. Thus, the firm may be 95% confident that foreign manufacturers control anywhere from 24. 72% to 43. 28% of the market.

Sample-Size Determination Before determining the necessary sample size, three questions must be answered: • • • How close do you want your sample estimate to be to the unknown parameter? (What is the desired bound, B? ) What do you want the desired confidence level (1 - ) to be so that the distance between your estimate and the parameter is less than or equal to B? What is your estimate of the variance (or standard deviation) of the population in question? } Bound, B

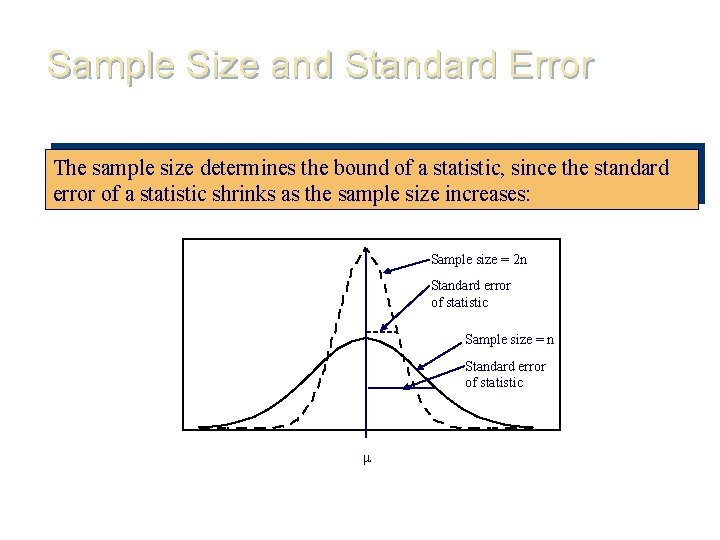
Sample Size and Standard Error The sample size determines the bound of a statistic, since the standard error of a statistic shrinks as the sample size increases: Sample size = 2 n Standard error of statistic Sample size = n Standard error of statistic

Minimum Sample Size: Mean and Proportion Minimum required sample size in estimating the population mean, m: z 2 s 2 n= 2 2 B Bound of estimate: B = z 2 s n Minimum required sample size in estimating the population proportion, $ p z 2 pq n= 2 2 B

Sample-Size Determination: Example A marketing research firm wants to conduct a survey to estimate the average amount spent on entertainment by each person visiting a popular resort. The people who plan the survey would like to determine the average amount spent by all people visiting the resort to within $120, with 95% confidence. From past operation of the resort, an estimate of the population standard deviation is σ = $400. What is the minimum required sample size?

Sample-Size for Proportion: Example The manufacturers of a sports car want to estimate the proportion of people in a given income bracket who are interested in the model. The company wants to know the population proportion, p, to within 0. 01 with 99% confidence. Current company records indicate that the proportion p may be around 0. 25. What is the minimum required sample size for this survey?