Estimating the Spatial Structure of a Stochastic Gravitational

Estimating the Spatial Structure of a Stochastic Gravitational Wave Background for Stef the an B Co LIGO allme llab Sc r ora ien tio tific n 12/14/2007 GWD Cam AW 12 Dece bridge, M mber A 14, 2 007 1

The generic Problem ? Detector 1 Spinning Earth Detector 2 12/14/2007 A spatially resolved map Only restriction: stationary signal Stefan Ballmer, Caltech 2

Some Definitions (sorry) • The Signal: • The Measurements: – Detector X-Power as function of time and frequency. • They are all independent, i. e. 12/14/2007 Stefan Ballmer, Caltech 3

The Expectation Value • Expectation value of Measurement: depends on time due to earth rotation • This defines the geometry factor 12/14/2007 Stefan Ballmer, Caltech 4

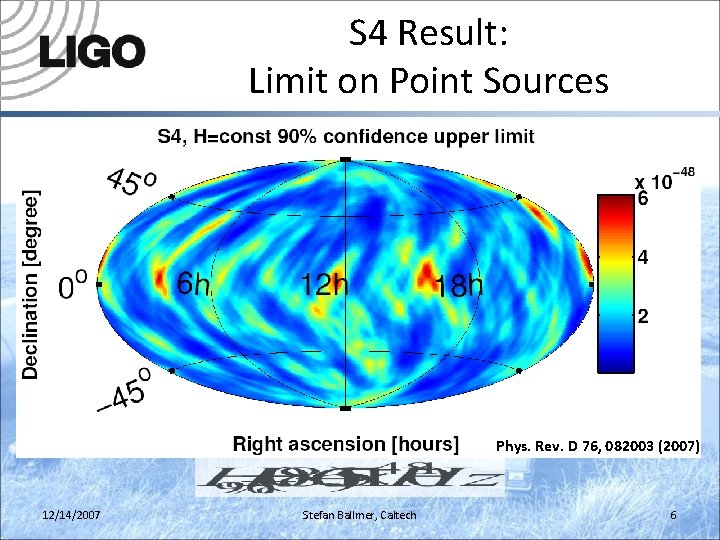
So far: Looking for Point Sources • For each pixel: • • Optimal to find isolated Point Sources Computationally inexpensive Neighboring pixels correlated (“blurred map”) S 4 result: Phys. Rev. D 76, 082003 (2007) 12/14/2007 Stefan Ballmer, Caltech 5

S 4 Result: Limit on Point Sources Phys. Rev. D 76, 082003 (2007) 12/14/2007 Stefan Ballmer, Caltech 6

What about that blur? • “Blur” described by covariance (Fisher) matrix: • In principle not hard to calculate, – But Γ needs to be inverted to calculate noise – Size = (# Pixel)2 – No exploitable symmetry for Pixel basis • S. Mitra et. al. , to be published in PRD – Fisher matrix not fully inverted 12/14/2007 Stefan Ballmer, Caltech 7

A better basis • Pixel basis not optimal for deconvolution – Does not respect rotational symmetry – No natural resolution cut-off • The obvious candidate: – Spherical Harmonics • Have all of the above 12/14/2007 Stefan Ballmer, Caltech 8

Spherical Harmonics • Maximum likelihood estimation gives: i. e. same as before • But symmetries imply structure: – Parity: – Rotational symmetry: 12/14/2007 Δl odd Γ = 0 (exact) m ≠ m’ Γ ≈ 0 (approx. ) Stefan Ballmer, Caltech 9

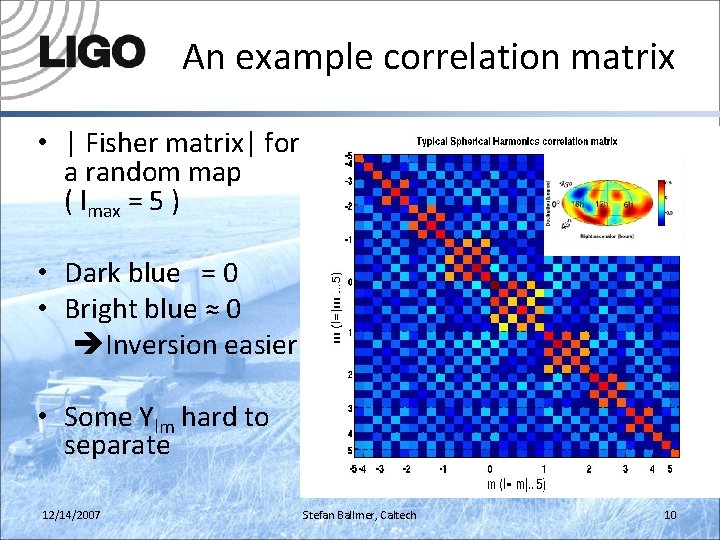
An example correlation matrix • | Fisher matrix| for a random map ( lmax = 5 ) • Dark blue = 0 • Bright blue ≈ 0 Inversion easier • Some Ylm hard to separate 12/14/2007 Stefan Ballmer, Caltech 10

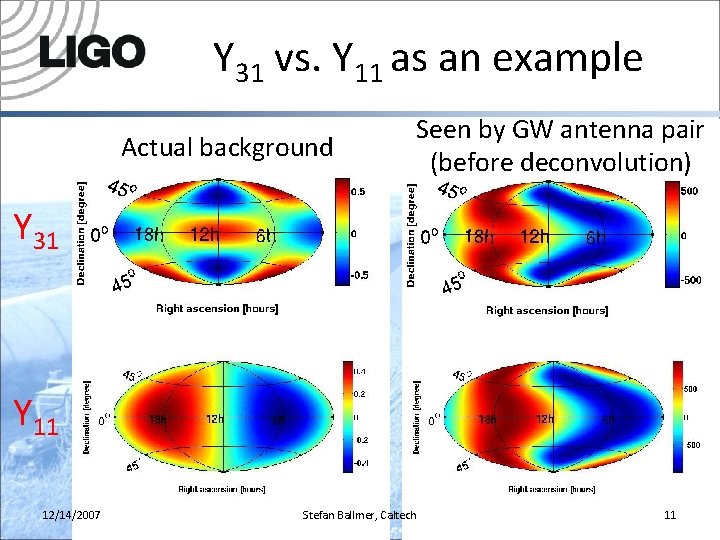
Y 31 vs. Y 11 as an example Actual background Seen by GW antenna pair (before deconvolution) Y 31 Y 11 12/14/2007 Stefan Ballmer, Caltech 11

Conclusion • Deconvolution allows estimation of spatial structure. • Spherical Harmonics is appropriate basis – But some Y hard to separate • Implementation Status – Analysis core exists in MATLAB – Further testing still required 12/14/2007 Stefan Ballmer, Caltech 12

TH EE ND 12/14/2007 13

12/14/2007 Stefan Ballmer, Caltech 14

What about that blur? Maximum likelihood formalism (1) • Model: – Distribution: Expectation value: • Probability distribution: …just Gaussian… 12/14/2007 Stefan Ballmer, Caltech 15

What about that blur? Maximum likelihood formalism (2) • Probability distribution: • Is maximal at • H(f): Spectral shape • γft, lm: Geometry factor 12/14/2007 Stefan Ballmer, Caltech 16