Estimating the longest increasing sequence in polylogarithmic time

Estimating the longest increasing sequence in polylogarithmic time C. Seshadhri (Sandia National Labs) Joint work with Michael Saks (Rutgers University) Sandia National Laboratories is a multi-program laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the U. S. Department of Energy's National Nuclear Security Administration under contract DE-AC 0494 AL 85000 1

The problem 4 n 10 9 15 17 20 18 4 19 3 Given array f: [n] → N, find (length of) Longest Increasing Subsequence (LIS) q n 24 Rather self-explanatory By now, textbook dynamic programming problem q q [CLRS 01] Chapter 15. 4 (Longest Common Subsequence), Starred Problem 15. 4 -6 [Schensted 61, Fredman 75] O(n log n) algorithm 2

Too much to read |LIS| is in range [0. 4 n, 0. 6 n] Algorithm 5 n 7 4 8 9 2 Array f is extremely large, so can’t read all of it q What can we say about LIS length, if we see very little? n q q |LIS| = LIS length Read only poly(log n) positions Obviously randomized 3

Uniform sample says nothing 2 1 4 3 6 5 8 7 10 9 n Choose uniform random sample of poly(log n) size |LIS| = n/2, but random sample always increasing n So not really that easy to learn about |LIS|… n 4

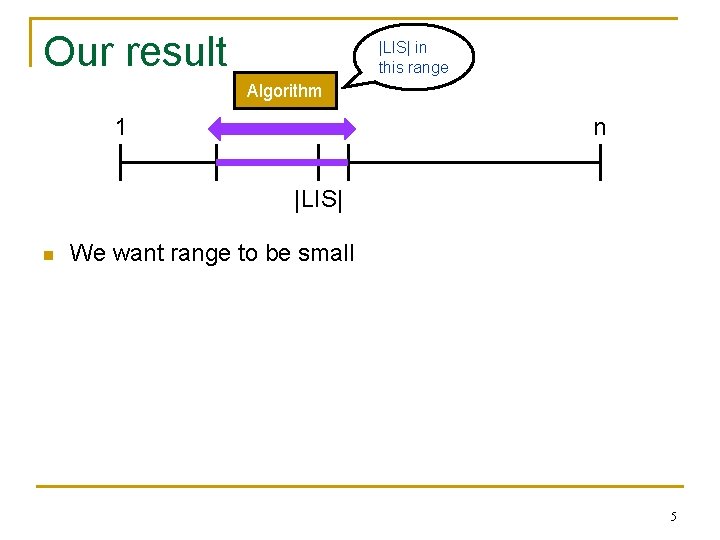
Our result |LIS| in this range Algorithm 1 n |LIS| n We want range to be small 5

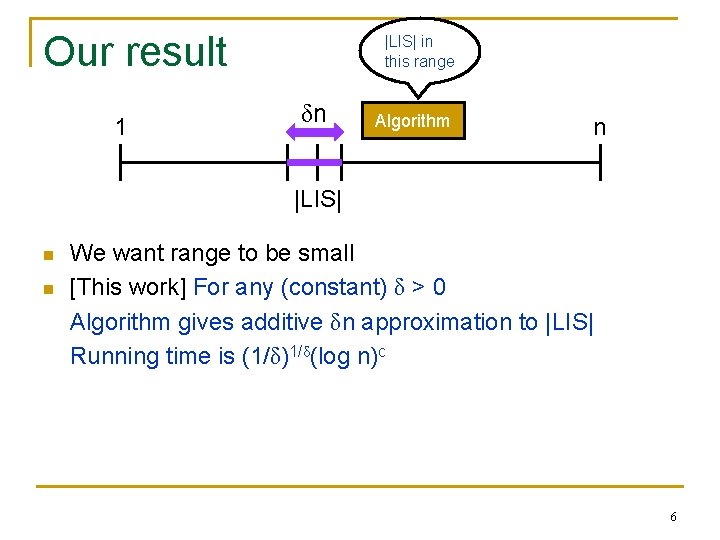
Our result 1 |LIS| in this range δn Algorithm n |LIS| n n We want range to be small [This work] For any (constant) δ > 0 Algorithm gives additive δn approximation to |LIS| Running time is (1/δ)1/δ(log n)c 6

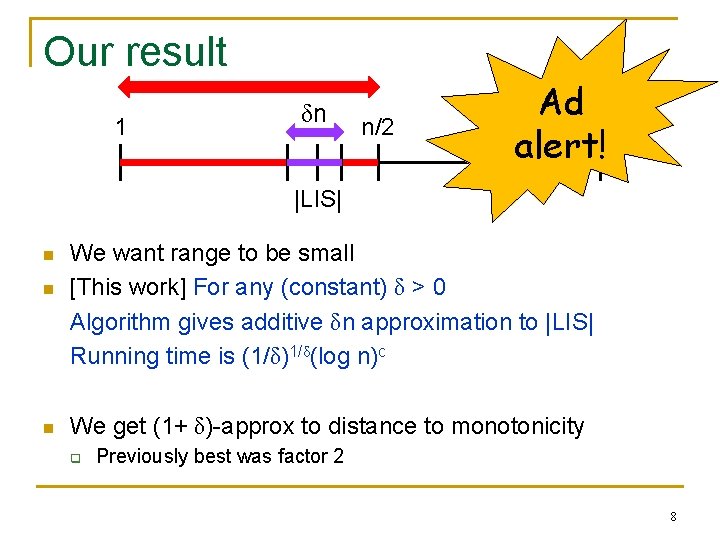
Our result 1 δn n/2 Ad n alert! |LIS| n n n We want range to be small [This work] For any (constant) δ > 0 Algorithm gives additive δn approximation to |LIS| Running time is (1/δ)1/δ(log n)c [Ailon Chazelle Liu S 03] [Parnas Ron Rubinfeld 03] Previous best: δ = ½ 7

Our result 1 δn n/2 Ad n alert! |LIS| n n n We want range to be small [This work] For any (constant) δ > 0 Algorithm gives additive δn approximation to |LIS| Running time is (1/δ)1/δ(log n)c We get (1+ δ)-approx to distance to monotonicity q Previously best was factor 2 8

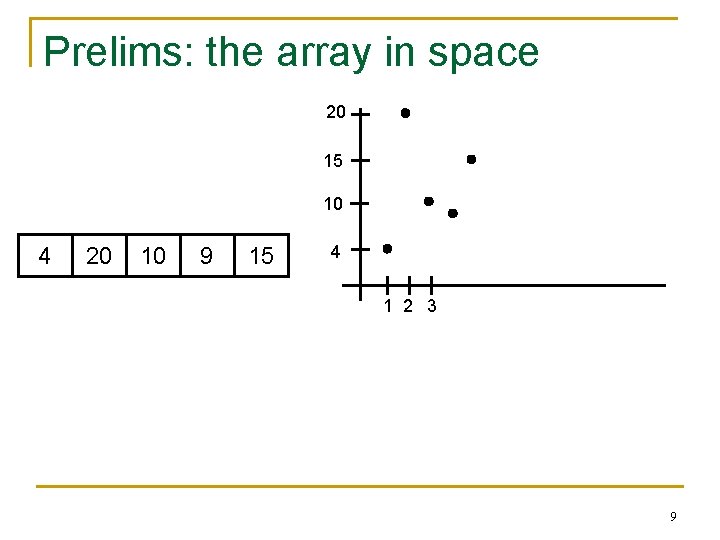
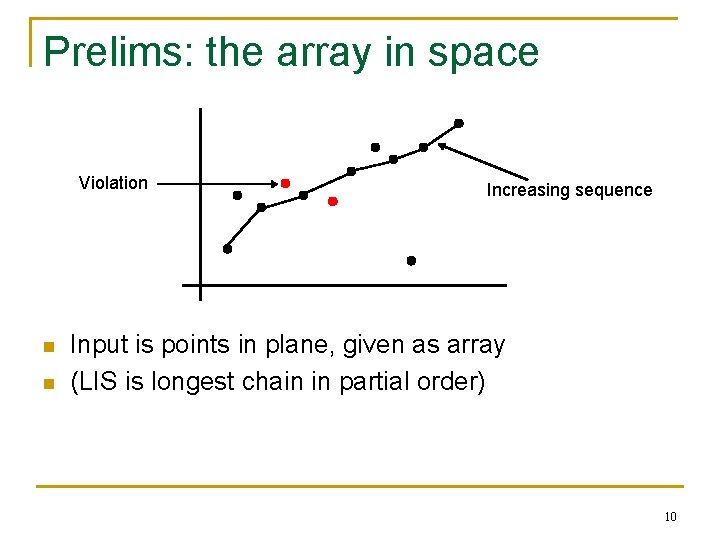
Prelims: the array in space 20 15 10 4 20 10 9 15 4 1 2 3 9

Prelims: the array in space Violation n n Increasing sequence Input is points in plane, given as array (LIS is longest chain in partial order) 10

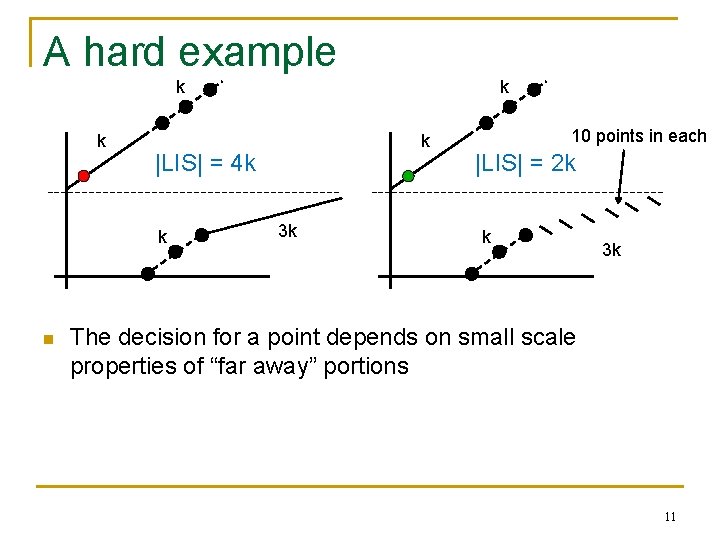
A hard example k k k |LIS| = 4 k k n k 3 k 10 points in each |LIS| = 2 k k 3 k The decision for a point depends on small scale properties of “far away” portions 11

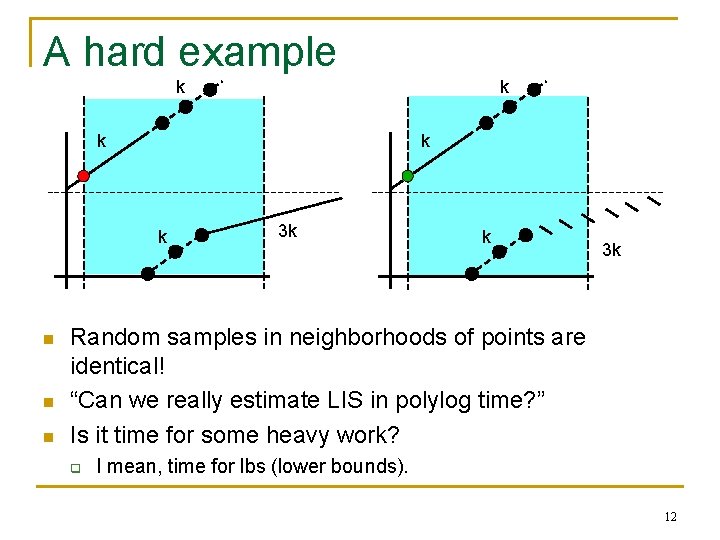
A hard example k k k n n n 3 k k 3 k Random samples in neighborhoods of points are identical! “Can we really estimate LIS in polylog time? ” Is it time for some heavy work? q I mean, time for lbs (lower bounds). 12

Outline (or lack thereof) n n Will I show proofs? No n Will I show the algorithm? Maybe n I will try to demonstrate the main insight n q By a series of thought experiments 13

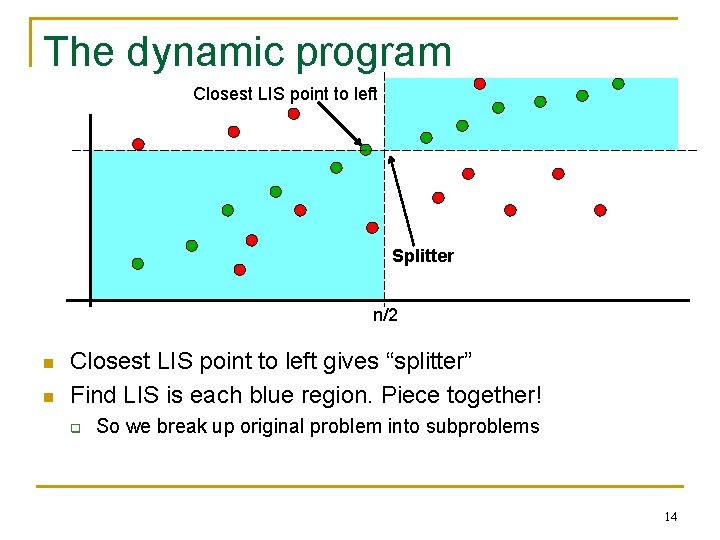
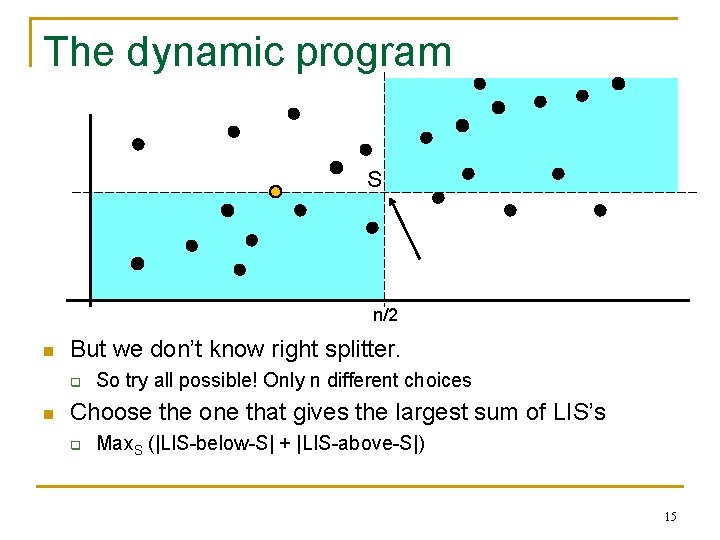
The dynamic program Closest LIS point to left Splitter n/2 n n Closest LIS point to left gives “splitter” Find LIS is each blue region. Piece together! q So we break up original problem into subproblems 14

The dynamic program S n/2 n But we don’t know right splitter. q n So try all possible! Only n different choices Choose the one that gives the largest sum of LIS’s q Max. S (|LIS-below-S| + |LIS-above-S|) 15

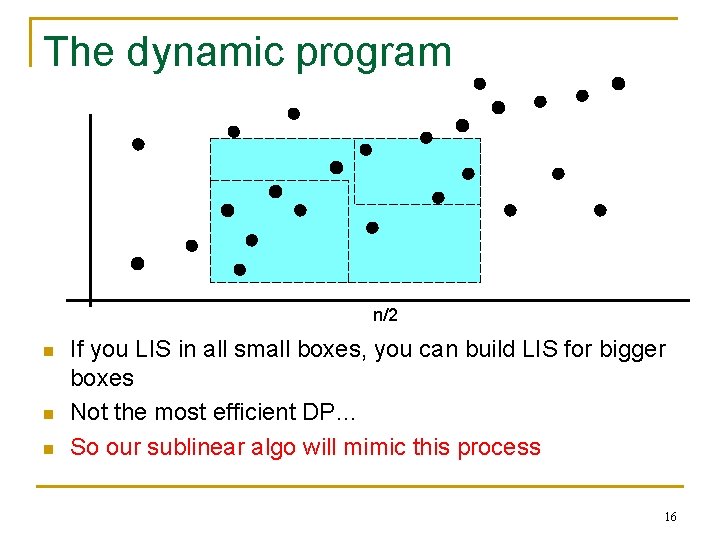
The dynamic program n/2 n n n If you LIS in all small boxes, you can build LIS for bigger boxes Not the most efficient DP… So our sublinear algo will mimic this process 16

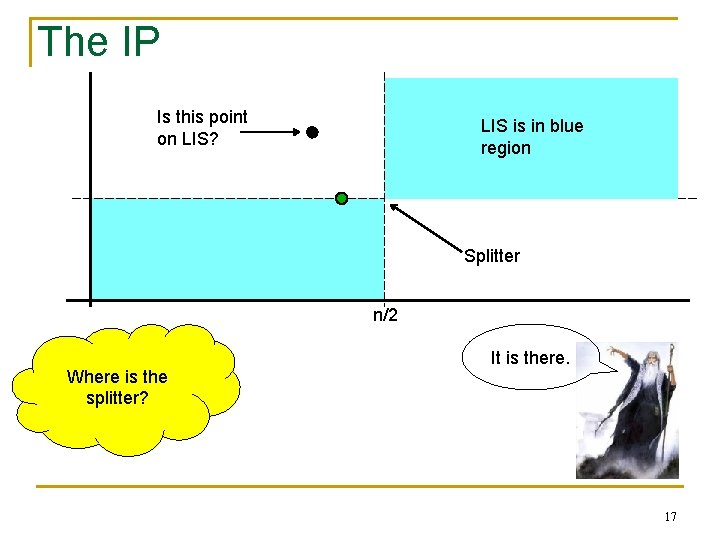
The IP Is this point on LIS? LIS is in blue region Splitter n/2 Where is the splitter? It is there. 17

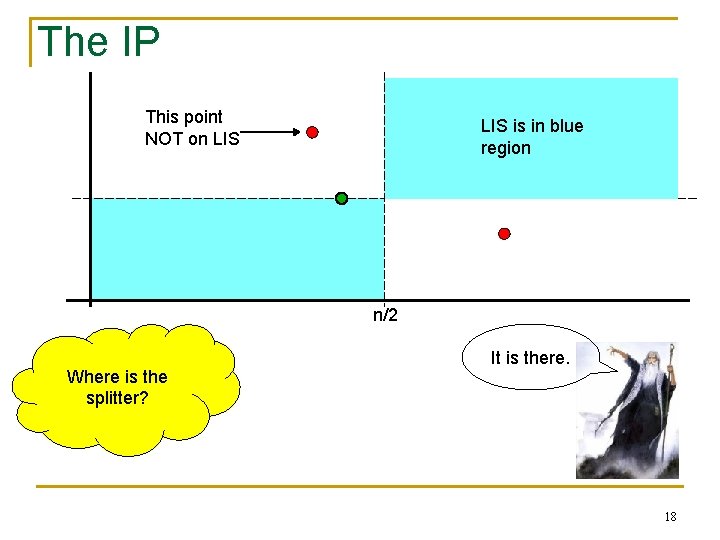
The IP This point NOT on LIS is in blue region n/2 Where is the splitter? It is there. 18

The IP n/2 I wish we knew the splitter in that region 3 n/4 It is there. 19

The IP n/2 I think I know what will happen next 5 n/8 3 n/4 You’re lucky I’m here 20

The IP n/2 I think I know what will happen next 5 n/8 3 n/4 You’re lucky I’m here 21

The IP n/2 I think I know what will happen next 5 n/8 3 n/4 You’re lucky I’m here 22

The interactive protocol n n If point stays in blue region till very end, then it is good (on LIS). Otherwise, bad. This takes (log n) steps, with the help of the wizard 23

The interactive protocol n n n If point stays in blue region till very end, then it is good (on LIS). Otherwise, bad. This takes (log n) steps, with the help of the wizard If we could simulate the wizard… 24

The interactive protocol n n n If point stays in blue region till very end, then it is good (on LIS). Otherwise, bad. This takes (log n) steps, with. Ifthe of the wizard What? ? youhelp could simulate the wizard, If we could simulate the wizard… you know the LIS! 25

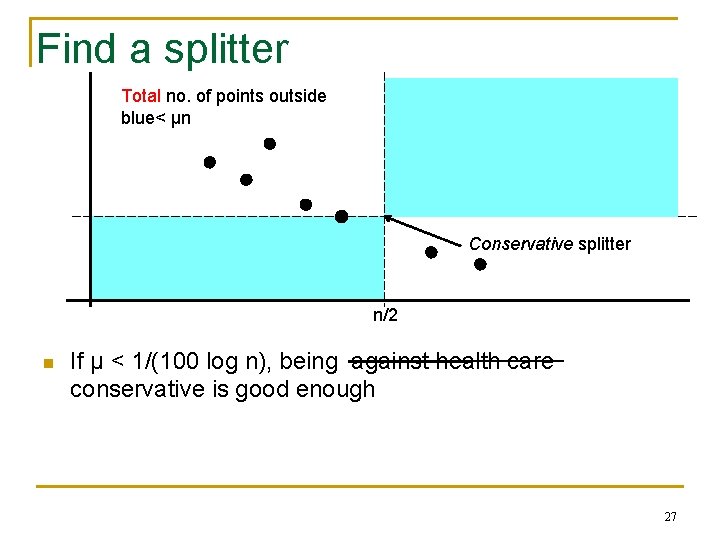
Find a splitter If very few LIS points outside blue, this is not a bad splitter n/2 n n Finding splitter may be hard, so try for approximate versions…? But how do we determine the number of LIS points? 26

Find a splitter Total no. of points outside blue< μn Conservative splitter n/2 n If μ < 1/(100 log n), being against health care conservative is good enough 27

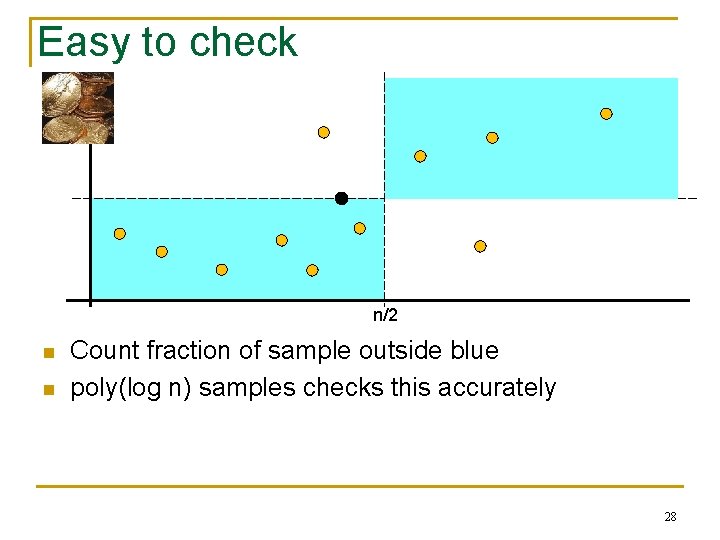
Easy to check n/2 n n Count fraction of sample outside blue poly(log n) samples checks this accurately 28

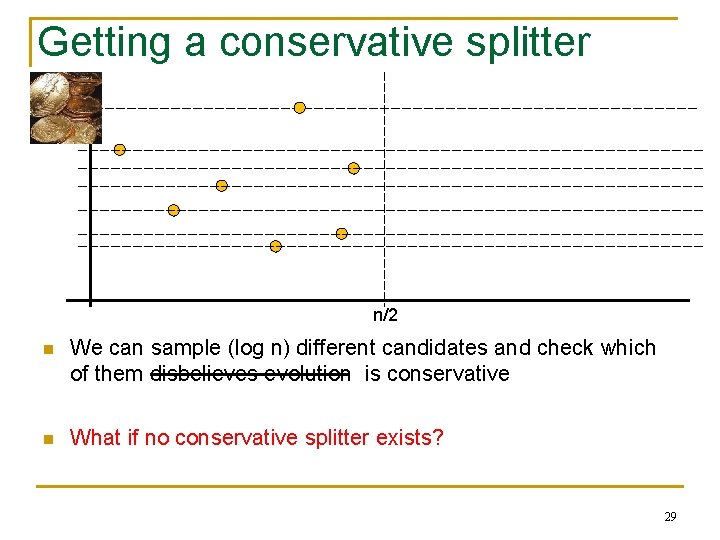
Getting a conservative splitter n/2 n We can sample (log n) different candidates and check which of them disbelieves evolution is conservative n What if no conservative splitter exists? 29

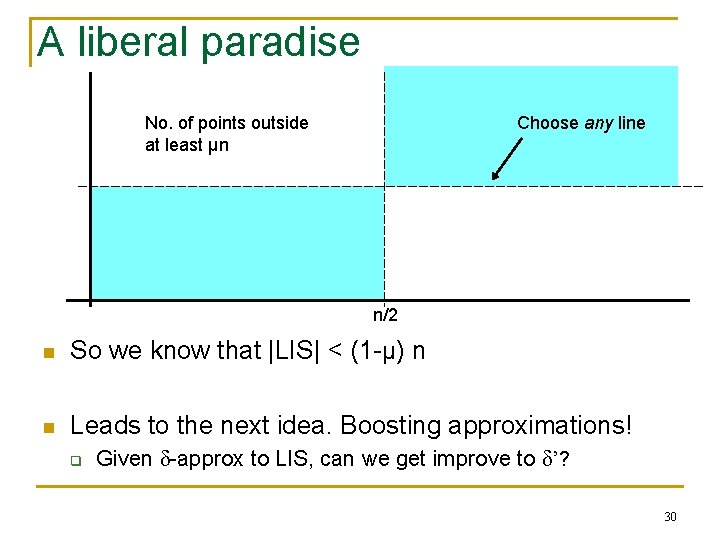
A liberal paradise No. of points outside at least μn Choose any line n/2 n So we know that |LIS| < (1 -μ) n n Leads to the next idea. Boosting approximations! q Given δ-approx to LIS, can we get improve to δ’? 30

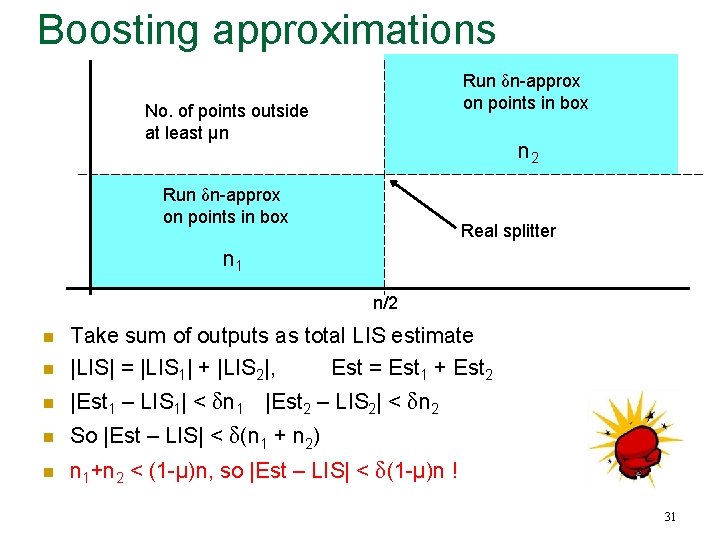
Boosting approximations Run δn-approx on points in box No. of points outside at least μn n 2 Run δn-approx on points in box Real splitter n 1 n/2 n Take sum of outputs as total LIS estimate |LIS| = |LIS 1| + |LIS 2|, Est = Est 1 + Est 2 n |Est 1 – LIS 1| < δn 1 |Est 2 – LIS 2| < δn 2 n So |Est – LIS| < δ(n 1 + n 2) n n 1+n 2 < (1 -μ)n, so |Est – LIS| < δ(1 -μ)n ! n 31

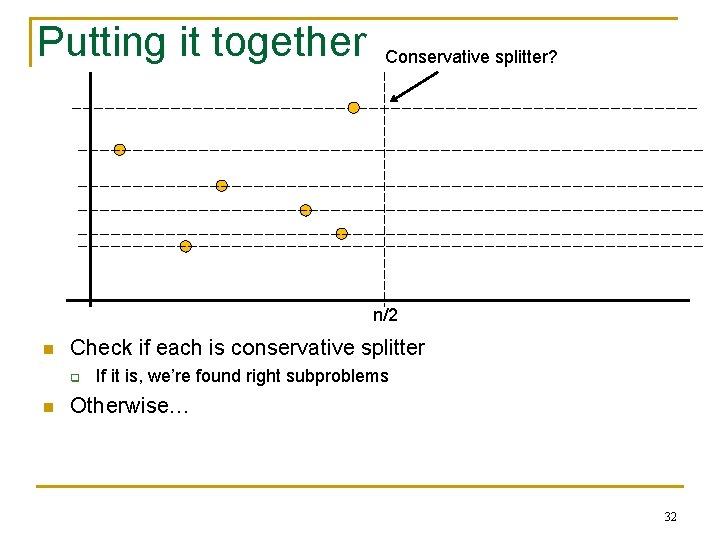
Putting it together Conservative splitter? n/2 n Check if each is conservative splitter q n If it is, we’re found right subproblems Otherwise… 32

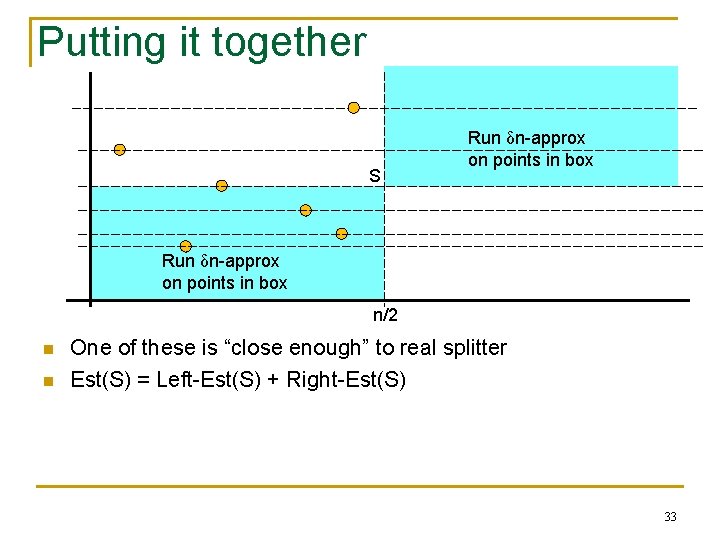
Putting it together S Run δn-approx on points in box n/2 n n One of these is “close enough” to real splitter Est(S) = Left-Est(S) + Right-Est(S) 33

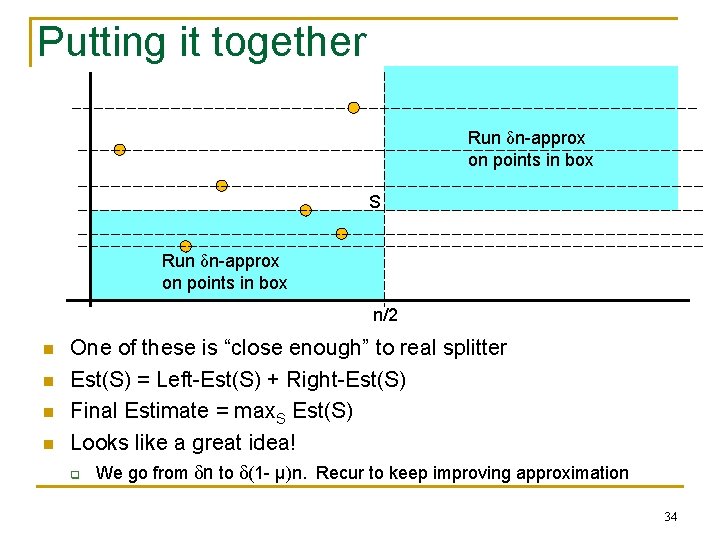
Putting it together Run δn-approx on points in box S Run δn-approx on points in box n/2 n n One of these is “close enough” to real splitter Est(S) = Left-Est(S) + Right-Est(S) Final Estimate = max. S Est(S) Looks like a great idea! q We go from δn to δ(1 - μ)n. Recur to keep improving approximation 34

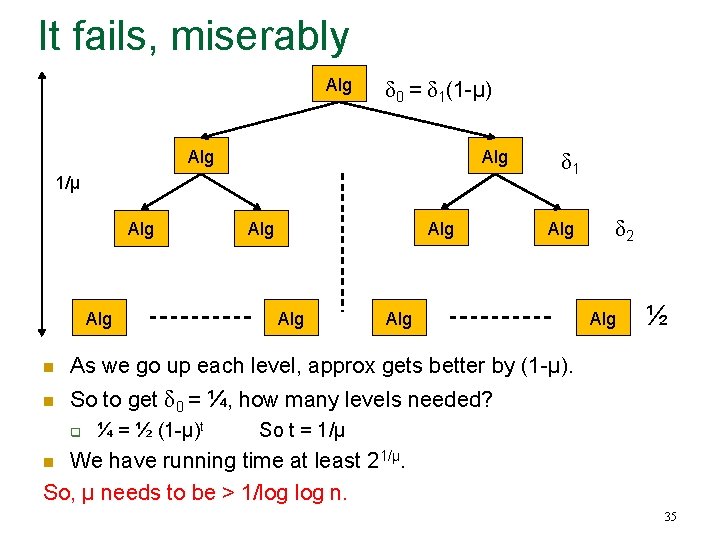
It fails, miserably Alg δ 0 = δ 1(1 -μ) Alg 1/μ Alg Alg Alg δ 1 Alg n As we go up each level, approx gets better by (1 -μ). n So to get δ 0 = ¼, how many levels needed? q ¼ = ½ (1 -μ)t δ 2 Alg ½ So t = 1/μ We have running time at least 21/μ. So, μ needs to be > 1/log n. n 35

Find a splitter Total no. of points outside blue< μn Conservative splitter n/2 n If μ < 1/(100 log n), being against health care conservative is good enough 36

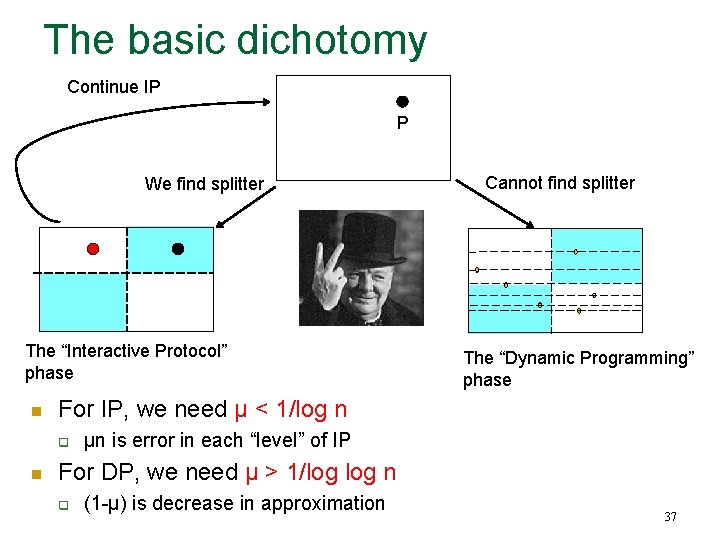
The basic dichotomy Continue IP P We find splitter The “Interactive Protocol” phase n The “Dynamic Programming” phase For IP, we need μ < 1/log n q n Cannot find splitter μn is error in each “level” of IP For DP, we need μ > 1/log n q (1 -μ) is decrease in approximation 37

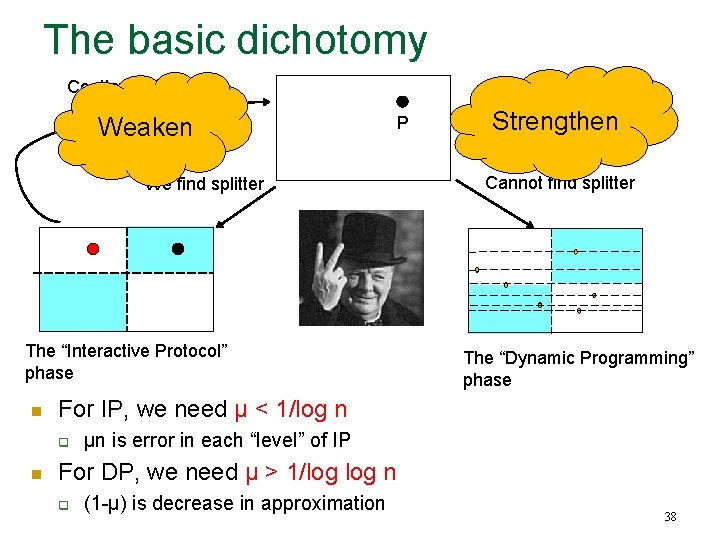
The basic dichotomy Continue IP Weaken We find splitter The “Interactive Protocol” phase n Strengthen Cannot find splitter The “Dynamic Programming” phase For IP, we need μ < 1/log n q n P μn is error in each “level” of IP For DP, we need μ > 1/log n q (1 -μ) is decrease in approximation 38

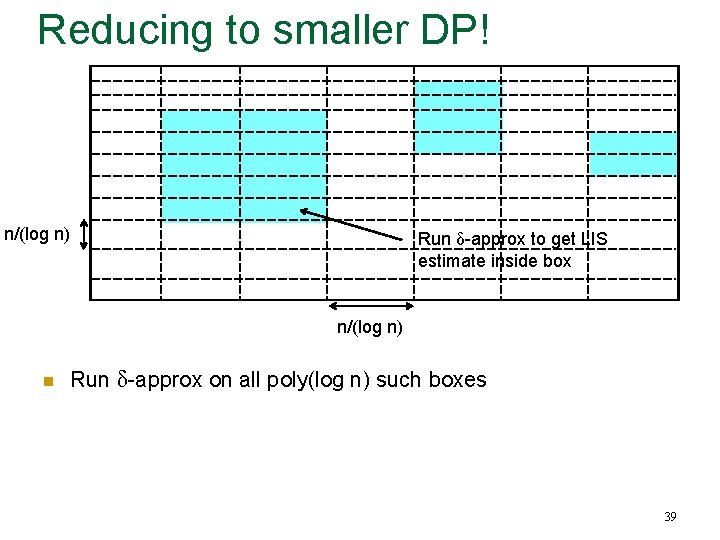
Reducing to smaller DP! n/(log n) Run δ-approx to get LIS estimate inside box n/(log n) n Run δ-approx on all poly(log n) such boxes 39

Reducing to smaller DP! Chain n/(log n) n n Run δ-approx on all poly(log n) such boxes Use Dynamic Program to find chain with largest sum of estimates q q Longest path in DAG Can solve in poly(log n) time 40

Dichotomy theorem OR Either it is easy to find the right subproblems One can go from δ-approx to (δ-δ 2)-approx by a (log n) sized DP 41

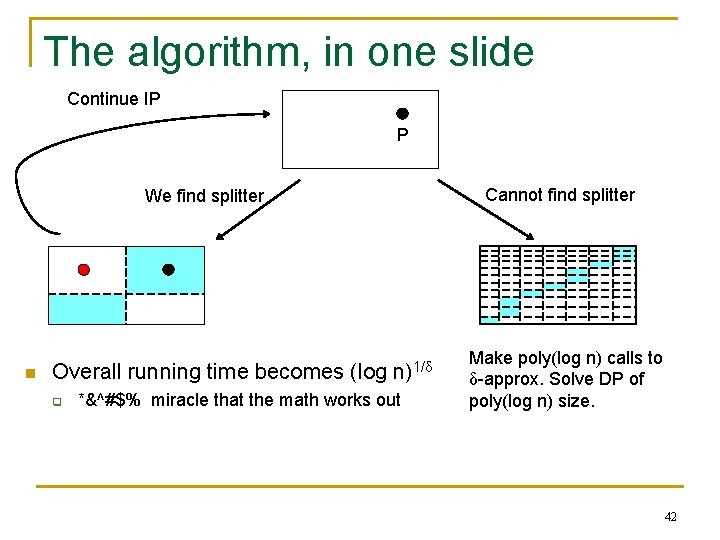
The algorithm, in one slide Continue IP P Cannot find splitter We find splitter n Overall running time becomes (log q n)1/δ *&^#$% miracle that the math works out Make poly(log n) calls to δ-approx. Solve DP of poly(log n) size. 42

The even better version n n Don’t exactly solve this dynamic program! Use our sublinear algo to approximately solve in (loglog n) time. Then do it recursively… q n It’s painful It’s all Greek: α β γ δ ε ζ λ μ ξ q We had ν, but got rid of it 43

What next? n n Sublinear dynamic programming! We get (1/δ)1/δ (log n)c time. Can we get (log n)/δ time? q n Would be extremely cool. Completely optimal Applications for other dynamic programs? q q q How does one find the “right” subproblems in sublinear time? Generalize the dichotomy Longest common subsequence/edit distance…? 44

Ask and you shall know… 45