Estimating the distribution of the incubation period of

Estimating the distribution of the incubation period of HIV/AIDS Marloes H. Maathuis Joint work with: Piet Groeneboom and Jon A. Wellner

Incubation period Time between HIV infection and onset of AIDS HIV AIDS 1985 1996 Incubation period 11 years
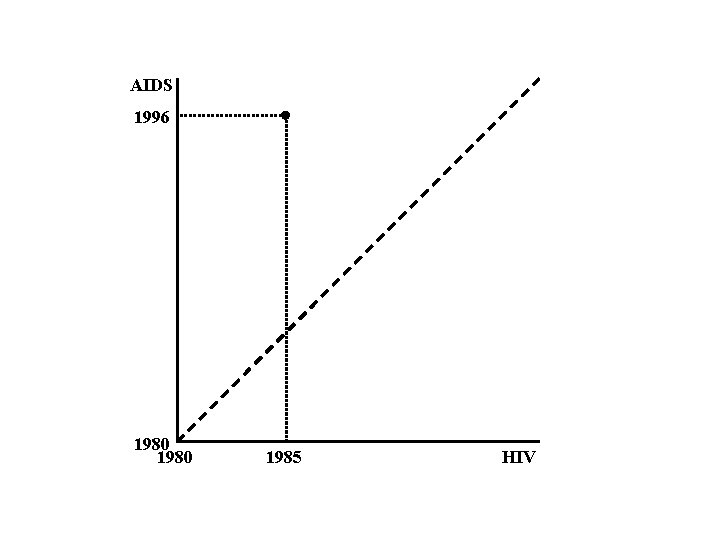
AIDS 1996 1980 1985 HIV
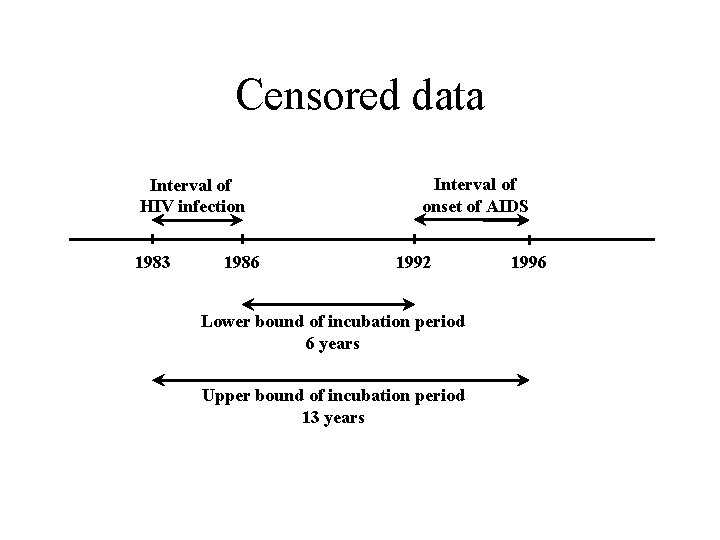
Censored data Interval of HIV infection 1983 1986 Interval of onset of AIDS 1992 Lower bound of incubation period 6 years Upper bound of incubation period 13 years 1996
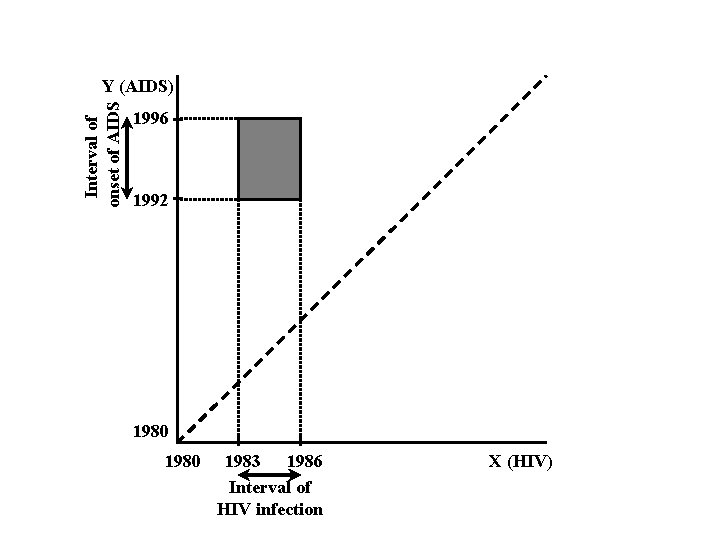
Interval of onset of AIDS Y (AIDS) 1996 1992 1980 1983 1986 Interval of HIV infection X (HIV)
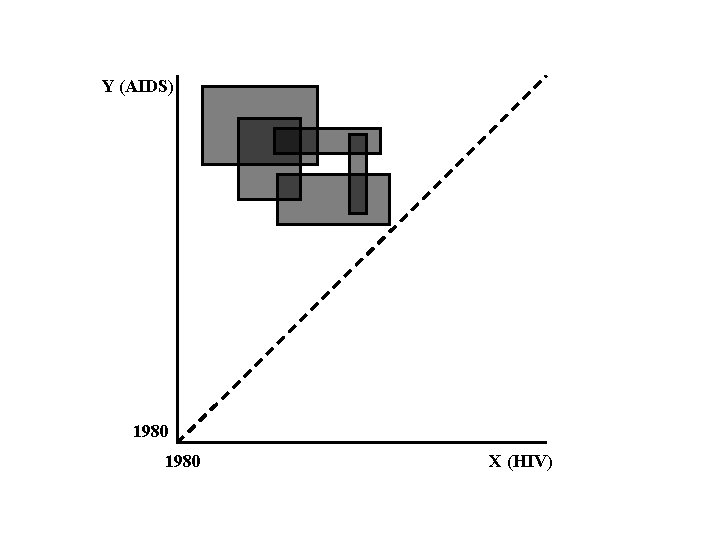
Y (AIDS) 1980 X (HIV)

Distribution functions • Goal: estimate the distribution function of the incubation period of HIV/AIDS • Why? This is important for predicting the future course of the epidemic • Strategy: First estimate the 2 -dimensional distribution



Main focus • Nonparametric maximum likelihood estimator (MLE) for 2 -dimensional distribution: – Computational aspects – Theoretical properties (consistency)

Computation of the MLE • Parameter reduction: determine the inner rectangles • Optimization: determine the amounts of mass assigned to the inner rectangles.
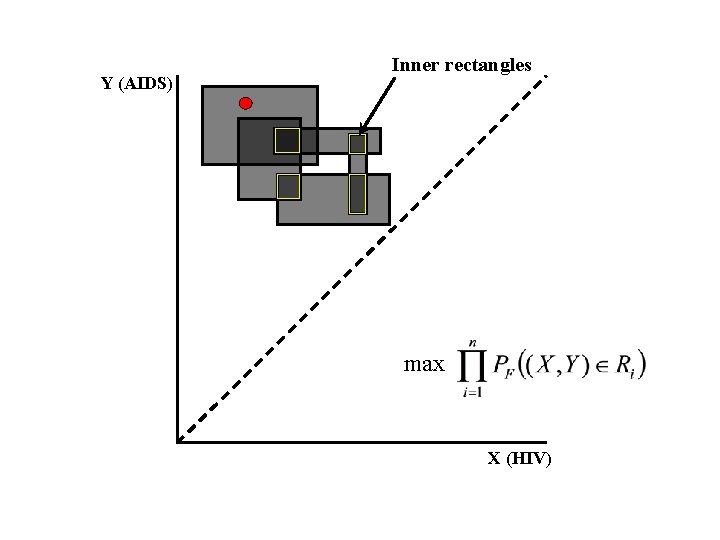
Y (AIDS) Inner rectangles max X (HIV)
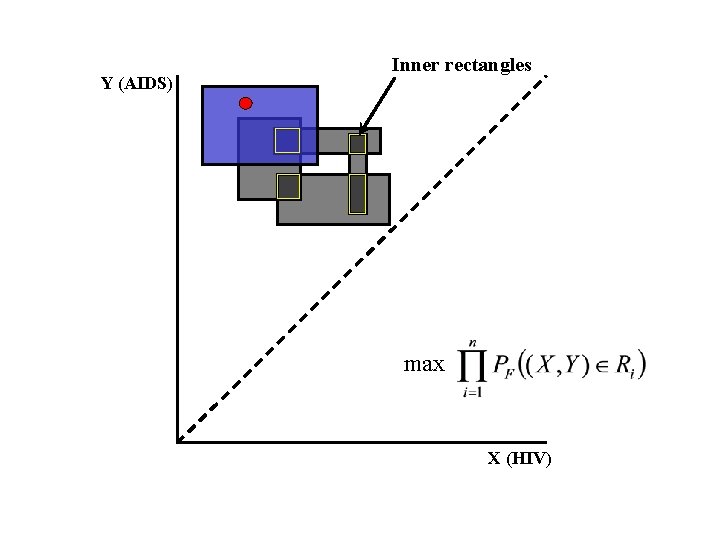
Y (AIDS) Inner rectangles max X (HIV)
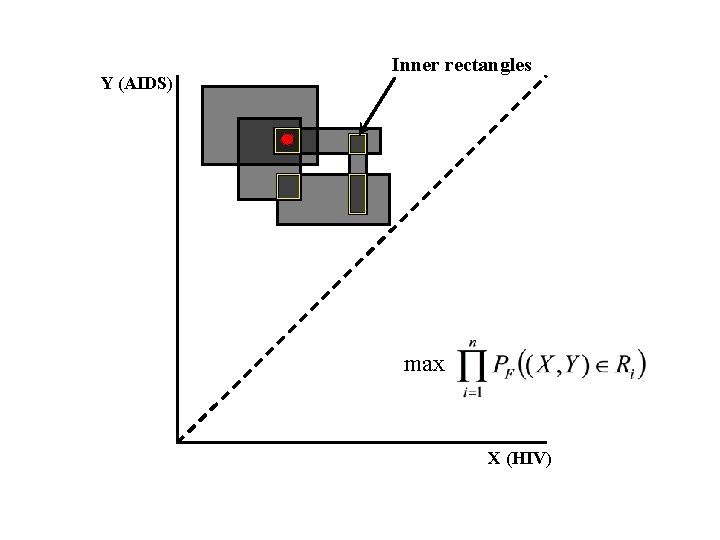
Y (AIDS) Inner rectangles max X (HIV)
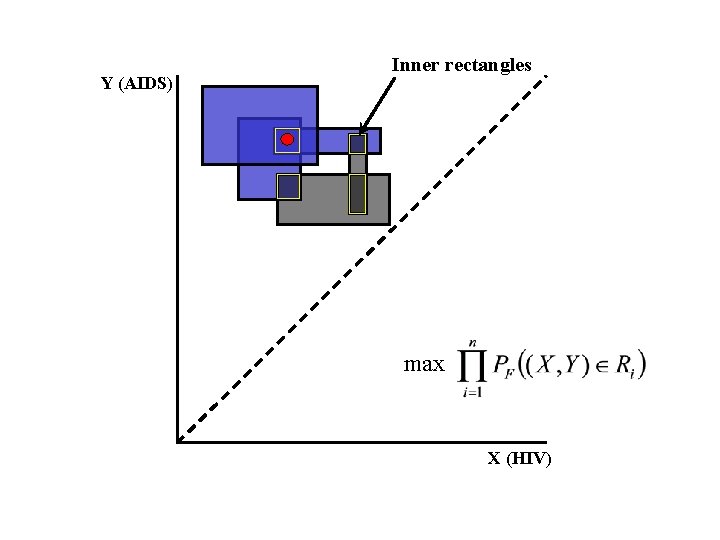
Y (AIDS) Inner rectangles max X (HIV)
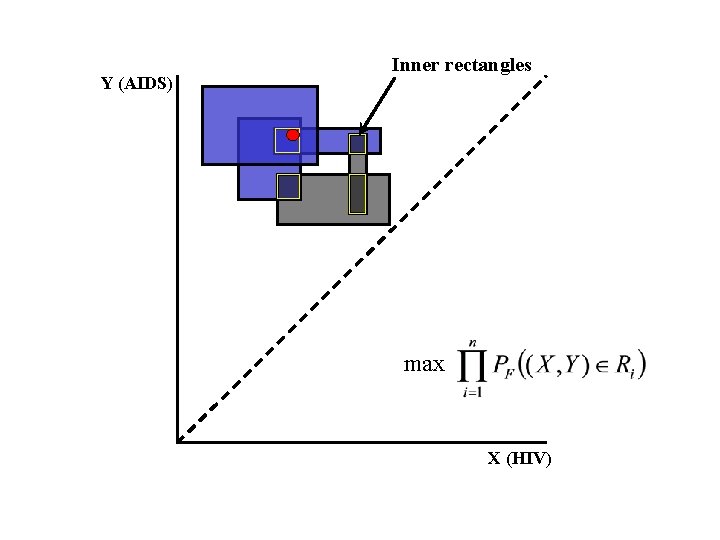
Y (AIDS) Inner rectangles max X (HIV)
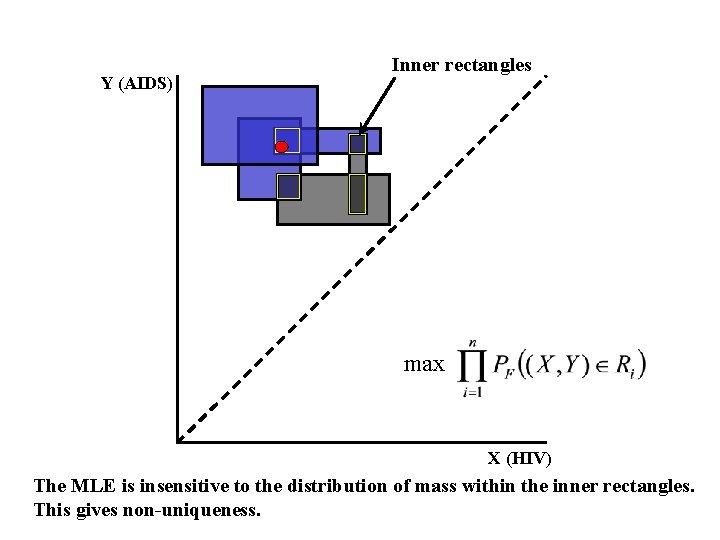
Y (AIDS) Inner rectangles max X (HIV) The MLE is insensitive to the distribution of mass within the inner rectangles. This gives non-uniqueness.
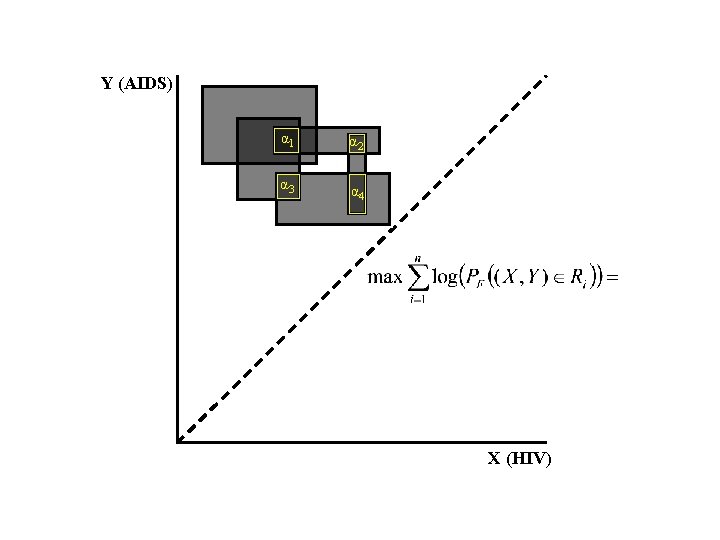
Y (AIDS) α 1 α 2 α 3 α 4 X (HIV)
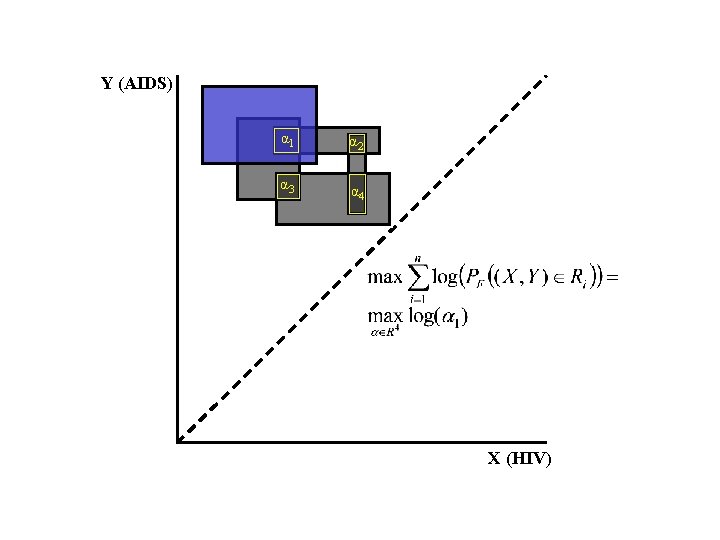
Y (AIDS) α 1 α 2 α 3 α 4 X (HIV)
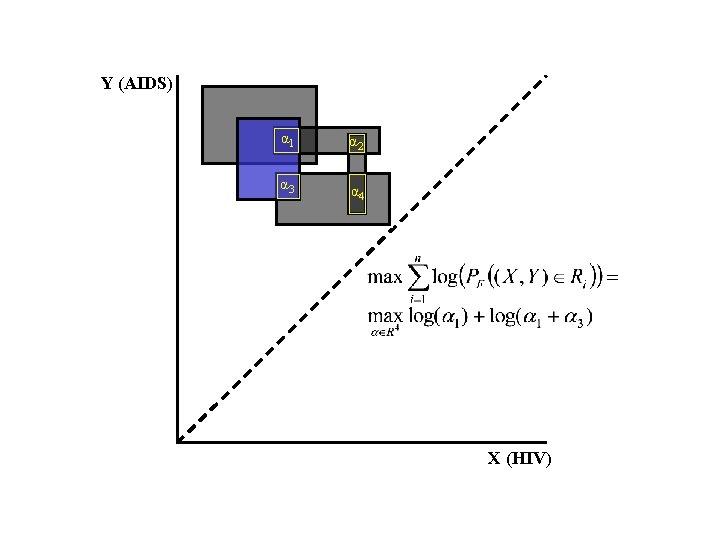
Y (AIDS) α 1 α 2 α 3 α 4 X (HIV)
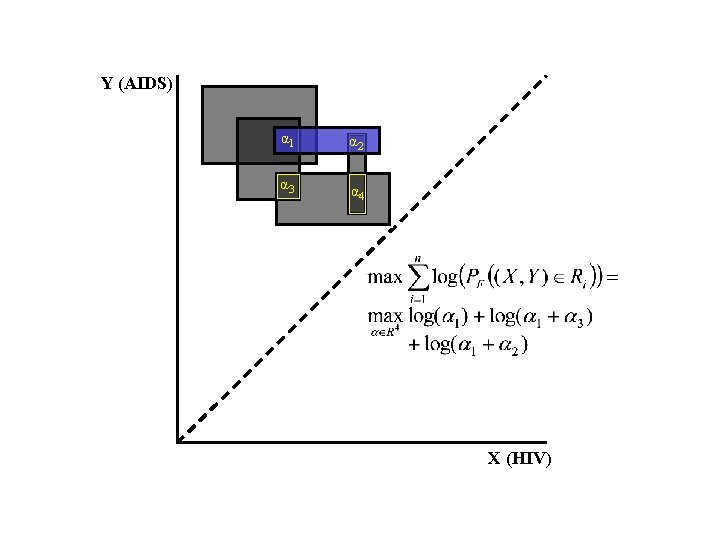
Y (AIDS) α 1 α 2 α 3 α 4 X (HIV)
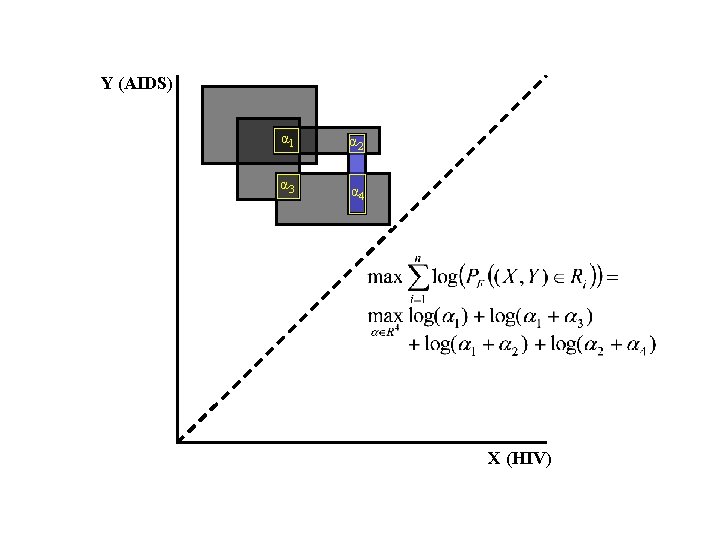
Y (AIDS) α 1 α 2 α 3 α 4 X (HIV)
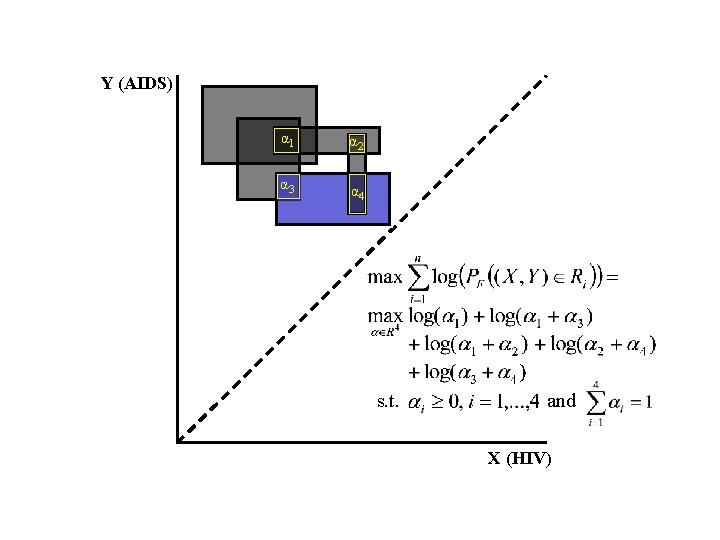
Y (AIDS) α 1 α 2 α 3 α 4 s. t. and X (HIV)
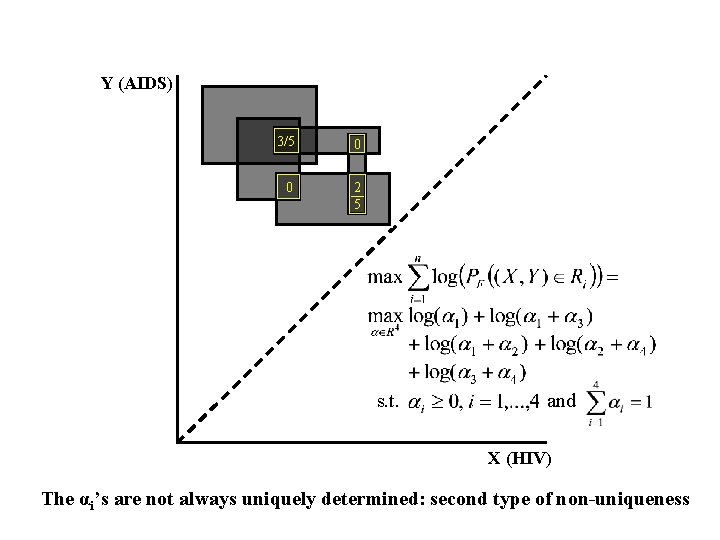
Y (AIDS) 3/5 0 0 2 5 s. t. and X (HIV) The αi’s are not always uniquely determined: second type of non-uniqueness
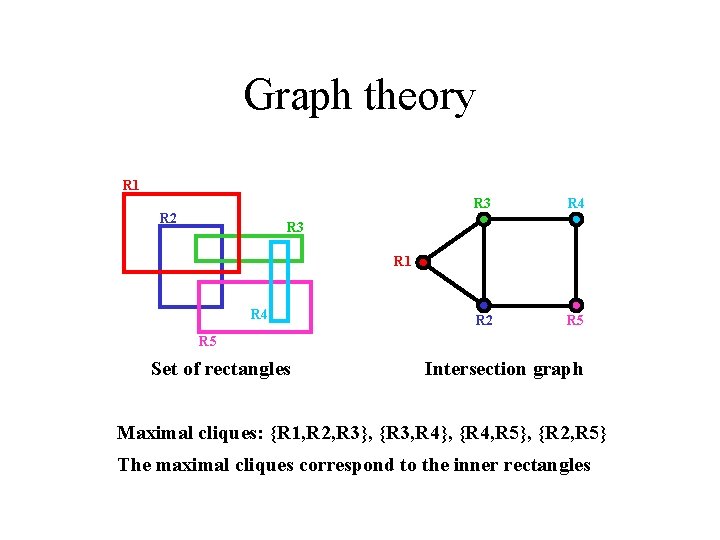
Graph theory R 1 R 2 R 3 R 4 R 2 R 5 R 3 R 1 R 4 R 5 Set of rectangles Intersection graph Maximal cliques: {R 1, R 2, R 3}, {R 3, R 4}, {R 4, R 5}, {R 2, R 5} The maximal cliques correspond to the inner rectangles

Existing reduction algorithms • Betensky and Finkelstein (1999) • Gentleman and Vandal (2001, 2002) • Song (2001) These algorithms are slow, complexity O(n 4) to O(n 5)

New algorithms • Max. Clique. Finder complexity ≤ O(n 2 log n) • Simple. Clique. Finder complexity O(n 2)
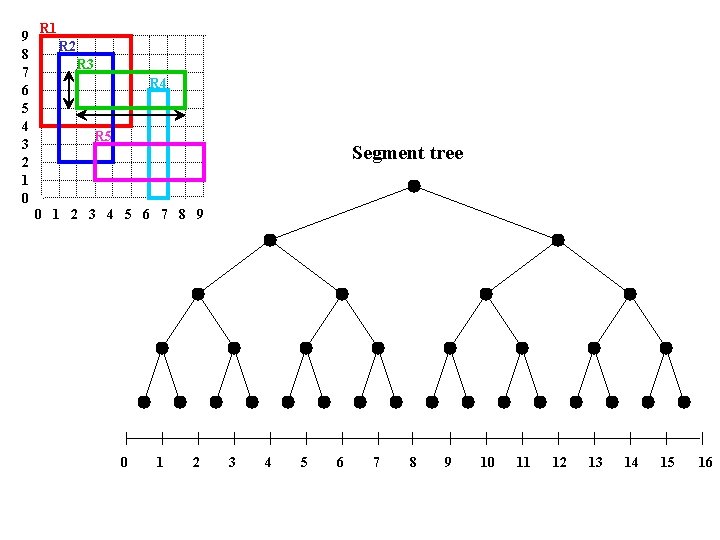
9 8 7 6 5 4 3 2 1 0 R 1 R 2 R 3 R 4 R 5 Segment tree 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
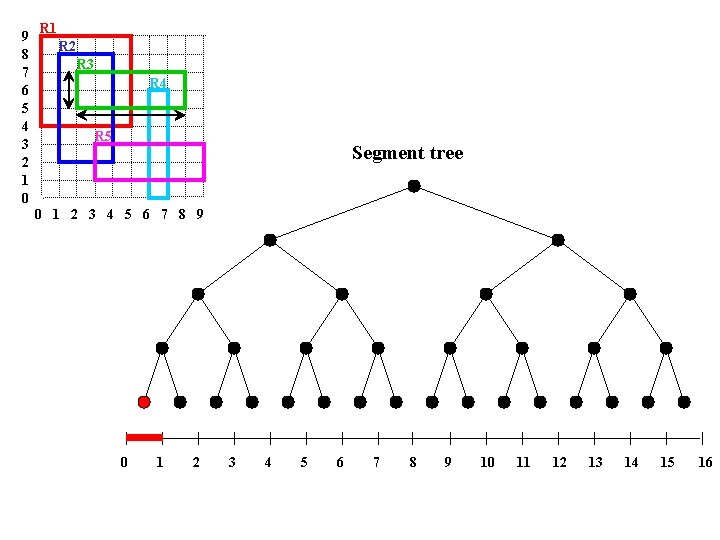
9 8 7 6 5 4 3 2 1 0 R 1 R 2 R 3 R 4 R 5 Segment tree 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
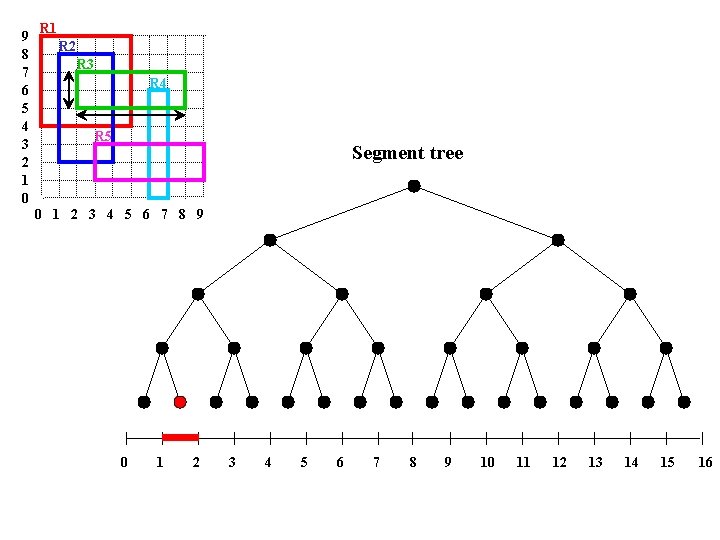
9 8 7 6 5 4 3 2 1 0 R 1 R 2 R 3 R 4 R 5 Segment tree 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
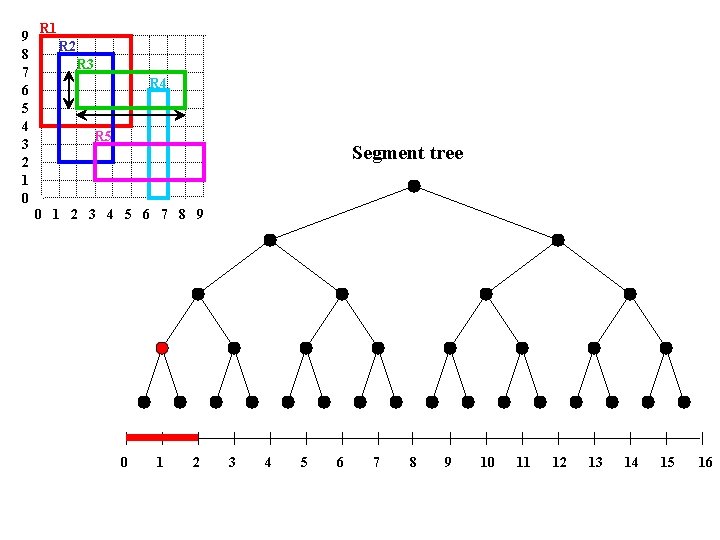
9 8 7 6 5 4 3 2 1 0 R 1 R 2 R 3 R 4 R 5 Segment tree 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
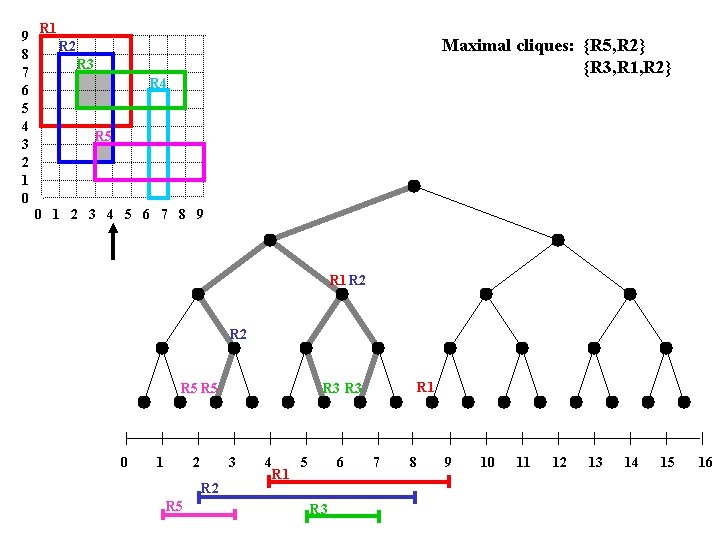
9 8 7 6 5 4 3 2 1 0 R 1 Maximal cliques: {R 5, R 2} {R 3, R 1, R 2} R 2 R 3 R 4 R 5 0 1 2 3 4 5 6 7 8 9 R 1 R 2 0 1 2 3 R 2 R 5 R 1 R 3 R 5 4 R 1 5 6 R 3 7 8 9 10 11 12 13 14 15 16
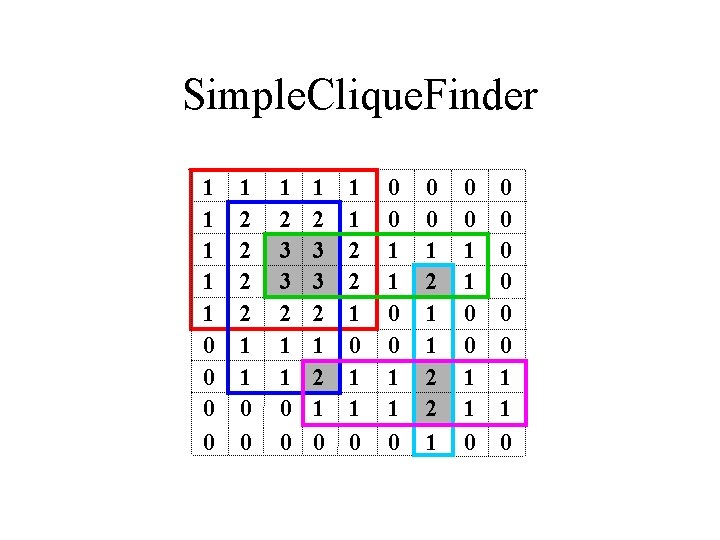
Simple. Clique. Finder 1 1 1 0 0 1 2 2 1 1 0 0 1 2 3 3 2 1 2 1 0 1 1 2 2 1 0 1 1 0 0 0 1 2 1 1 2 2 1 0 0 1 1 0 0 0 0 1 1 0


Computation of the MLE • Parameter reduction: determine the inner rectangles • Optimization: determine the amounts of mass assigned to the inner rectangles.

Optimization • High-dimensional convex constrained optimization problem

Amsterdam Cohort Study among injecting drug users • • Open cohort study Data available from 1985 to 1997 637 individuals were enrolled 216 individuals tested positive for HIV during the study

Model X: Y: Z = Y-X: U 1 , U 2: C: time of HIV infection time of onset of AIDS incubation period observation times for X censoring variable for Y (X, Y) and (U 1 , U 2, C) are independent
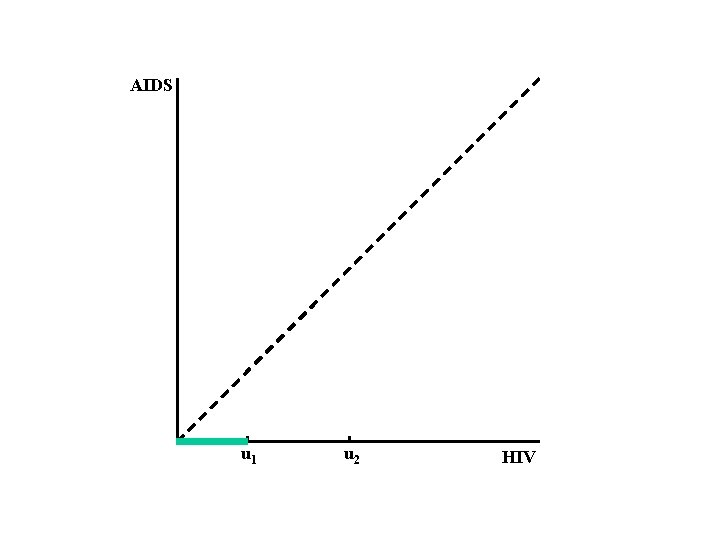
AIDS u 1 u 2 HIV
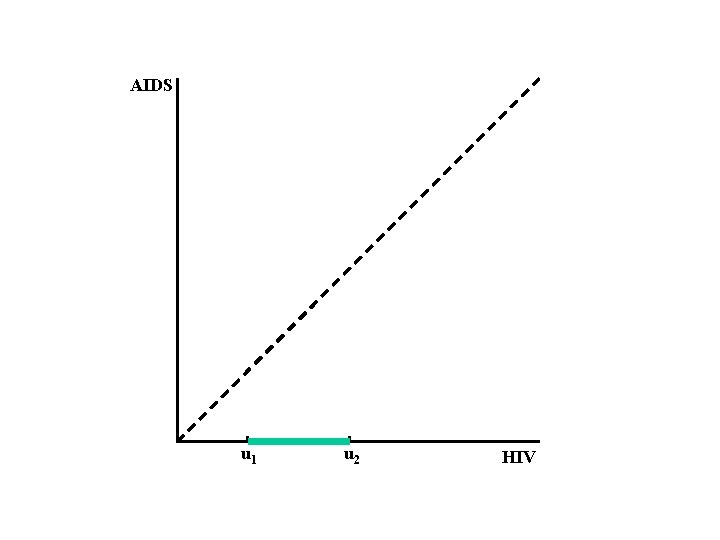
AIDS u 1 u 2 HIV
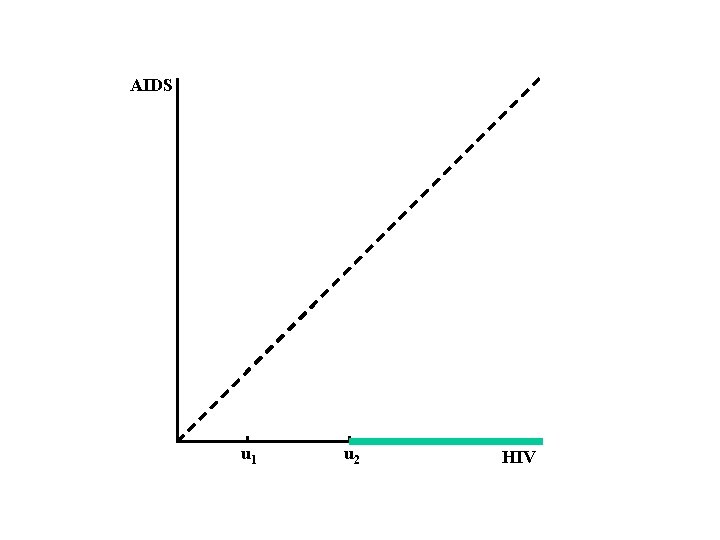
AIDS u 1 u 2 HIV
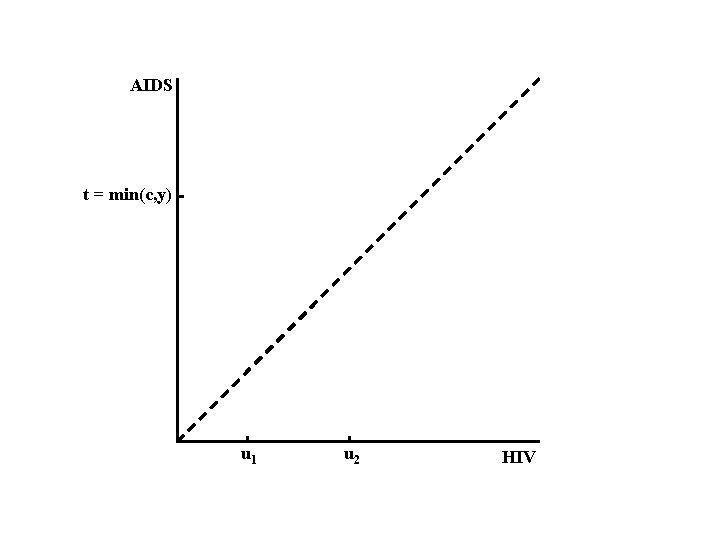
AIDS t = min(c, y) u 1 u 2 HIV
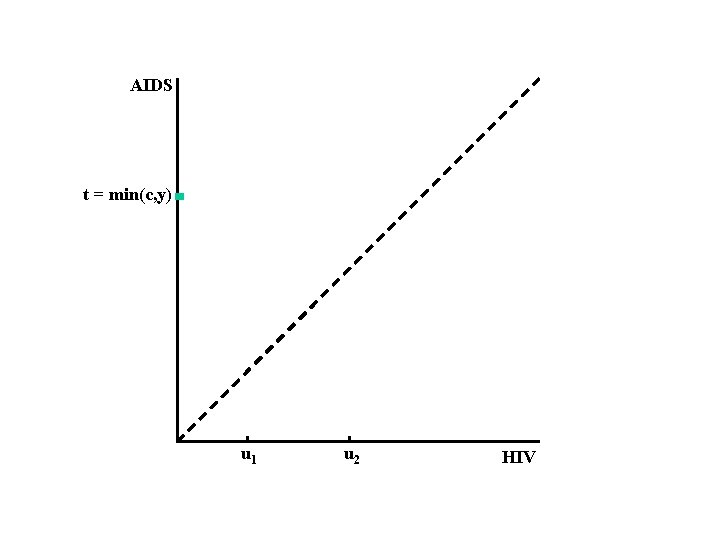
AIDS t = min(c, y) u 1 u 2 HIV
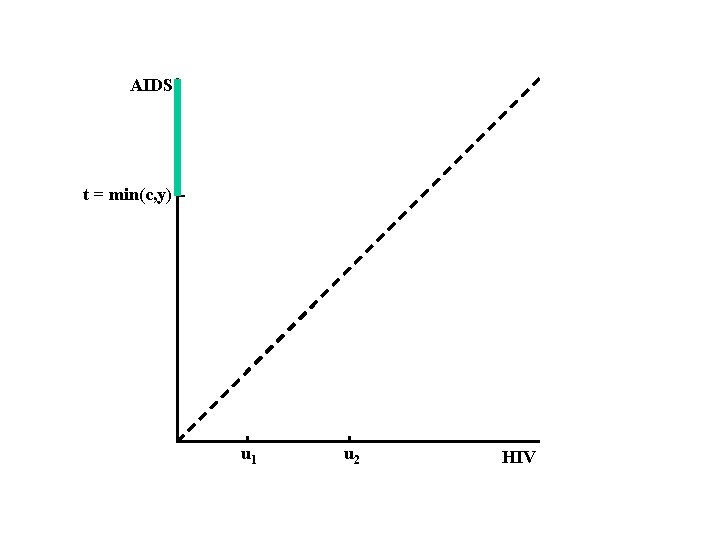
AIDS t = min(c, y) u 1 u 2 HIV
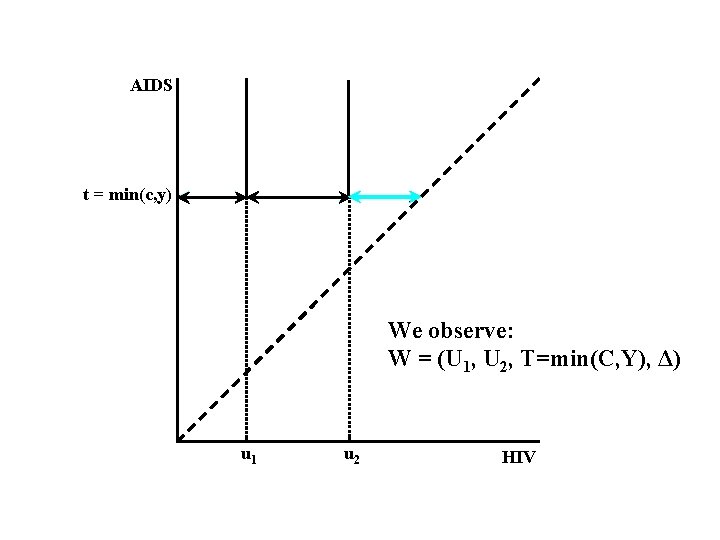
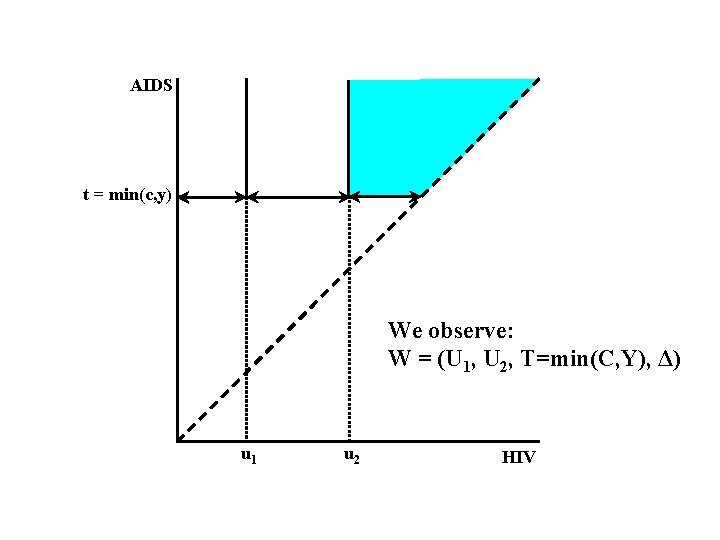
AIDS t = min(c, y) We observe: W = (U 1, U 2, T=min(C, Y), Δ) u 1 u 2 HIV

AIDS t = min(c, y) We observe: W = (U 1, U 2, T=min(C, Y), Δ) u 1 u 2 HIV
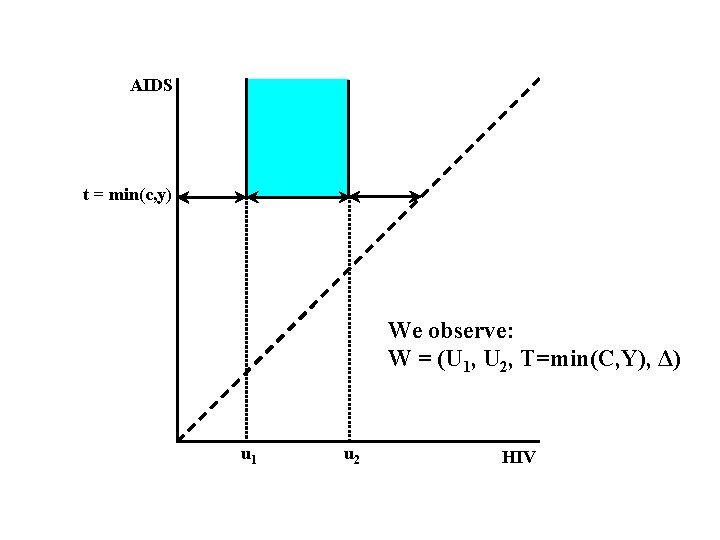
AIDS t = min(c, y) We observe: W = (U 1, U 2, T=min(C, Y), Δ) u 1 u 2 HIV
AIDS t = min(c, y) We observe: W = (U 1, U 2, T=min(C, Y), Δ) u 1 u 2 HIV

Inconsistency of the naive MLE
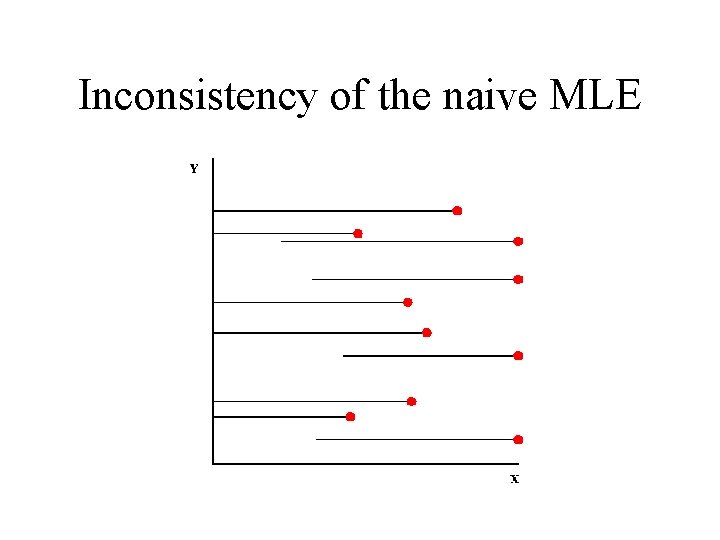
Inconsistency of the naive MLE
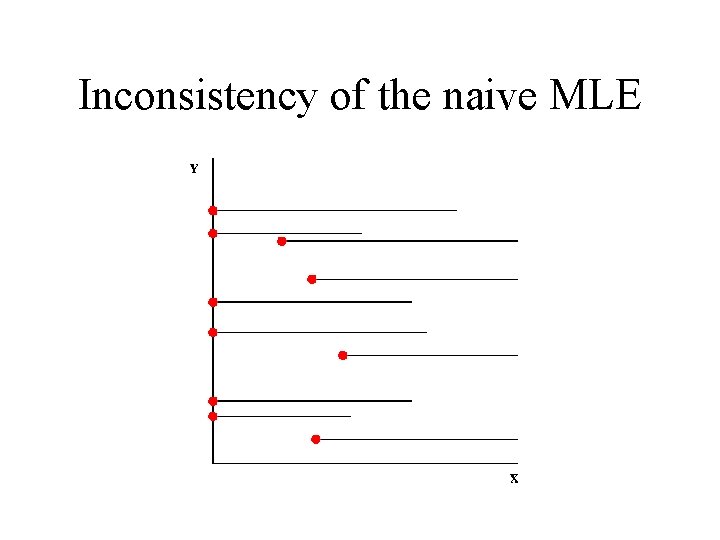
Inconsistency of the naive MLE
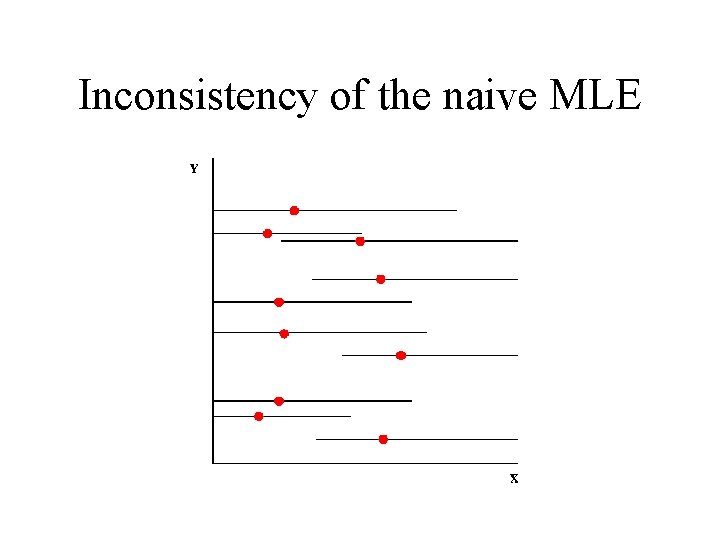
Inconsistency of the naive MLE

Methods to repair inconsistency • Transform the lines into strips • MLE on a sieve of piecewise constant densities • Kullback-Leibler approach
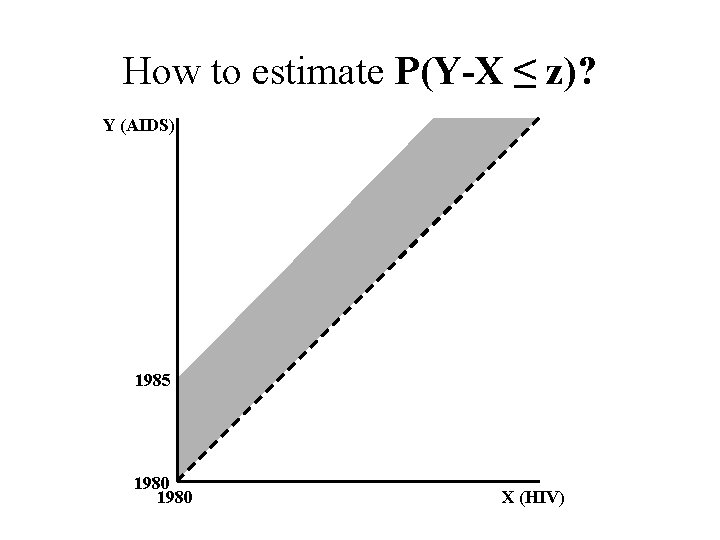
How to estimate P(Y-X ≤ z)? Y (AIDS) 1985 1980 X (HIV)







• The distribution function of the incubation period cannot be estimated consistently • What we can estimate consistently is P(Z ≤ z, Y ≤ 1997)


Conclusions (1) • We found the graph theoretic framework very useful • Our algorithms for the parameter reduction step are significantly faster than other methods. • We proved that in general the naive MLE is an inconsistent estimator for our AIDS model.

Conclusions (2) • We explored several methods to repair the inconsistency • The MLE can be very sensitive to small changes in the data • There is not enough information to estimate the incubation period consistently without making additional assumptions

- Slides: 65