Estimating Surface Normals in Noisy Point Cloud Data

Estimating Surface Normals in Noisy Point Cloud Data Niloy J. Mitra, An Nguyen Stanford University

The Normal Estimation Problem n Given Noisy PCD sampled from a curve/surface Normal Estimation for Noisy PCD Symposium on Computational Geometry

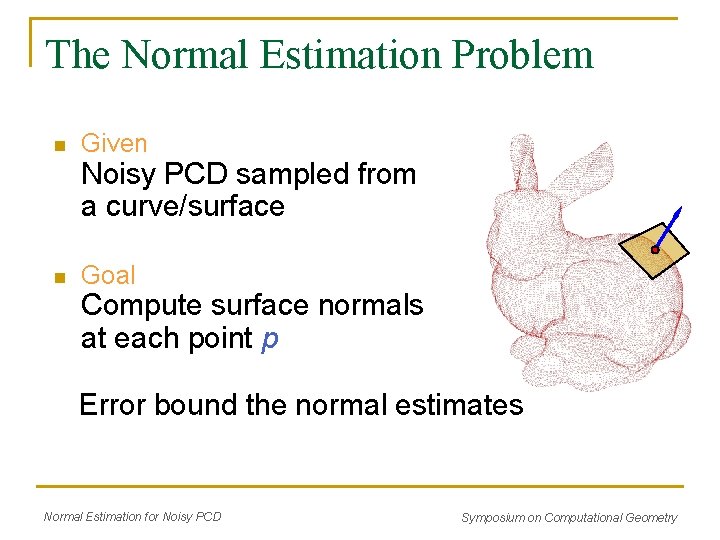
The Normal Estimation Problem n Given Noisy PCD sampled from a curve/surface n Goal Compute surface normals at each point p Error bound the normal estimates Normal Estimation for Noisy PCD Symposium on Computational Geometry

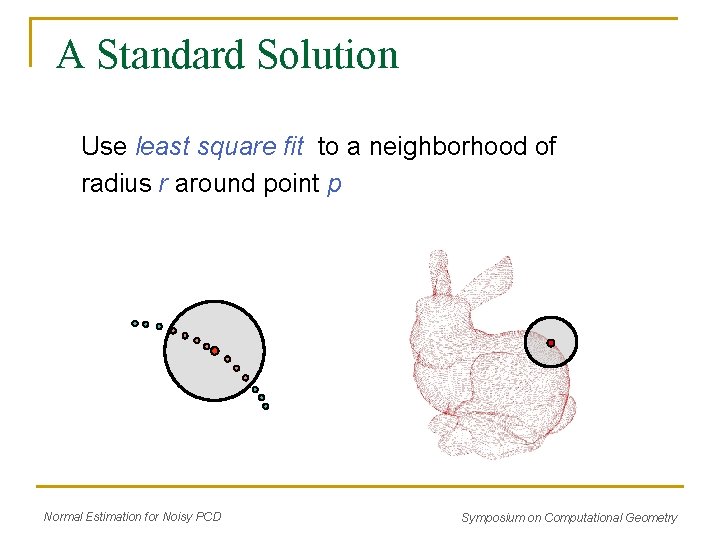
A Standard Solution Use least square fit to a neighborhood of radius r around point p Normal Estimation for Noisy PCD Symposium on Computational Geometry

A Standard Solution Use least square fit to a neighborhood of radius r around point p PROBLEM !! what neighborhood size to choose? Normal Estimation for Noisy PCD Symposium on Computational Geometry

Contributions of this paper n Study the effects of curvature, noise, sampling density on the choice of neighborhood size. n Use this insight to choose an optimal neighborhood size. n Compute bound on the estimation error. Normal Estimation for Noisy PCD Symposium on Computational Geometry

Outline n n n Problem statement Related work Neighborhood Size Estimation q q n Analysis in 2 D and 3 D Applications Future Work Normal Estimation for Noisy PCD Symposium on Computational Geometry

Related Work n Surface reconstruction q q q n crust, cocone, etc Guarantees about the surface normals Mostly works in absence of noise Curve/Surface fitting q q q point. Shop 3 D, point-set Works in presence of noise Performance guarantees? Normal Estimation for Noisy PCD Symposium on Computational Geometry

Least Square Fit n n a. Tp=c Assume best fit hyperplane: a. Tp=c Minimize n Reduces to the eigen-analysis of the covariance matrix n Smallest eigenvector of M is the estimate of the normal Normal Estimation for Noisy PCD Symposium on Computational Geometry

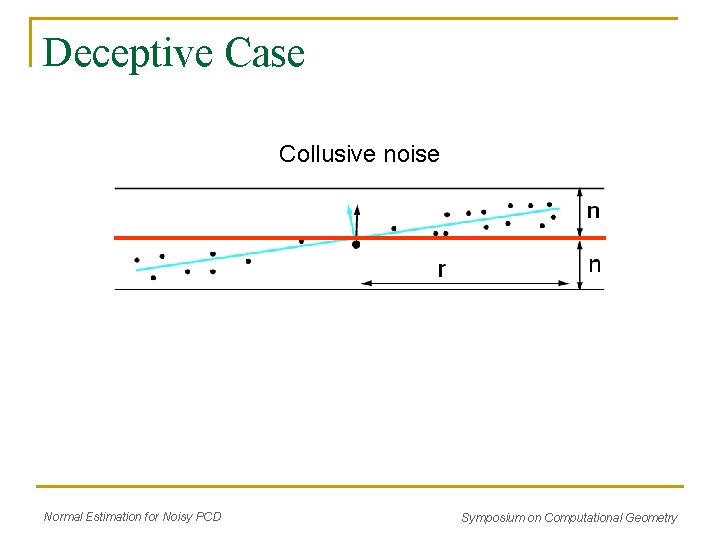
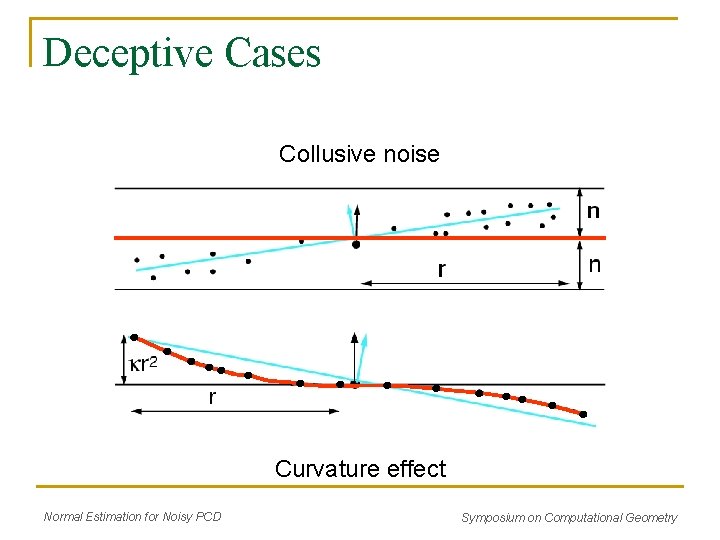
Deceptive Case Collusive noise Normal Estimation for Noisy PCD Symposium on Computational Geometry

Deceptive Cases Collusive noise Curvature effect Normal Estimation for Noisy PCD Symposium on Computational Geometry

Outline n n n Problem statement Related work Neighborhood Size Estimation q q n Analysis in 2 D and 3 D Applications Future Work Normal Estimation for Noisy PCD Symposium on Computational Geometry

Assumptions n Noise q q q n Independent of measurement Zero mean Variance is known (noise need not be bounded) Data q q Sampling criterion satisfied Evenly distributed data n q To prevent biased estimates Curvature is bounded Normal Estimation for Noisy PCD Symposium on Computational Geometry

Sampling Criteria (2 D) Sampling density • lower bound (like Nyquist rate) • upper bound (to prevent biased fits) Evenly distributed Number of points in a disc of radius r bounded above and below by (1)r ( , ) sampling condition [Dey et. al. ] implies evenly distributed. Normal Estimation for Noisy PCD Symposium on Computational Geometry

Modeling (2 D) n At a point O y x O 2 r q q q Points of PCD inside a disc of radius r comes from a segment of the curve y = g(x) define the curve for all x [-r, r] Bounded curvature: |g’’(x)|< for all x Additive Noise(n) in y-direction (x, g(x)+n) r, n/r assumed to be small Normal Estimation for Noisy PCD Symposium on Computational Geometry

Proof Idea n Eigen-analysis of covariance matrix Normal Estimation for Noisy PCD Symposium on Computational Geometry

Proof Idea n n covariance matrix let, =(|m 12|+m 22)/m 11 Normal Estimation for Noisy PCD Symposium on Computational Geometry

Proof Idea n n covariance matrix let, =(|m 12|+m 22)/m 11 error angle bounded by, to bound estimation error, need to bound Normal Estimation for Noisy PCD Symposium on Computational Geometry

Bounding Terms of M n For evenly distributed samples it follows, Normal Estimation for Noisy PCD Symposium on Computational Geometry

Bounding m 12 n n Evenly sampled distribution Noise and measurement are uncorrelated q E(xn)= E(x)E(n)= 0 q Var(xn)= (1)r 2 n 2 Chebyshev Inequality q bound with probability (1 - ) Finally, Normal Estimation for Noisy PCD Symposium on Computational Geometry

Bounding Estimation Error =(|m 12|+m 22)/m 11 Normal Estimation for Noisy PCD Symposium on Computational Geometry

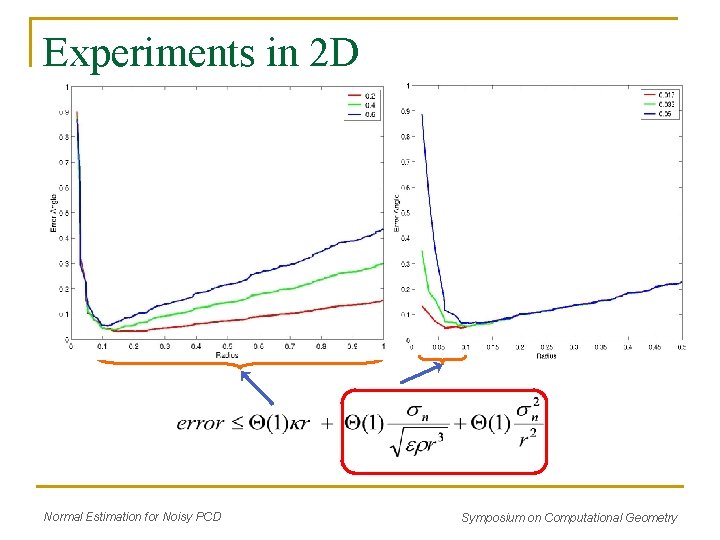
Final Result in 2 D • = 0, take as large a neighborhood as possible Normal Estimation for Noisy PCD Symposium on Computational Geometry

Final Result in 2 D • = 0, take as large a neighborhood as possible • n = 0 take as small a neighborhood as possible Normal Estimation for Noisy PCD Symposium on Computational Geometry

Experiments in 2 D Normal Estimation for Noisy PCD Symposium on Computational Geometry

Result for 3 D A similar but involved analysis results in, A good choice of r is, Normal Estimation for Noisy PCD Symposium on Computational Geometry

How can we use this result? n Need to q q q know estimate suitable values for estimate locally Normal Estimation for Noisy PCD Symposium on Computational Geometry

Estimating c 1, c 2 Exact normals known at almost all points c 1=1, c 2=4 • same constants used for following results Normal Estimation for Noisy PCD Symposium on Computational Geometry

Algorithm n n For each point, start with k =15 Iterate and refine (maximum of 10 steps) q Compute r, , [Gumhold et al. ] locally q Use them to compute rnew q knew = rnew 2 old q Stop if n n k>threshold k saturates Normal Estimation for Noisy PCD Symposium on Computational Geometry

Effect of Curvature on Neighborhood Size 1 x noise Normal Estimation for Noisy PCD Symposium on Computational Geometry

Effect of Noise on Neighborhood Size 1 x noise Normal Estimation for Noisy PCD 2 x noise Symposium on Computational Geometry

Estimation Error > 5 1 x noise Normal Estimation for Noisy PCD o 2 x noise Symposium on Computational Geometry

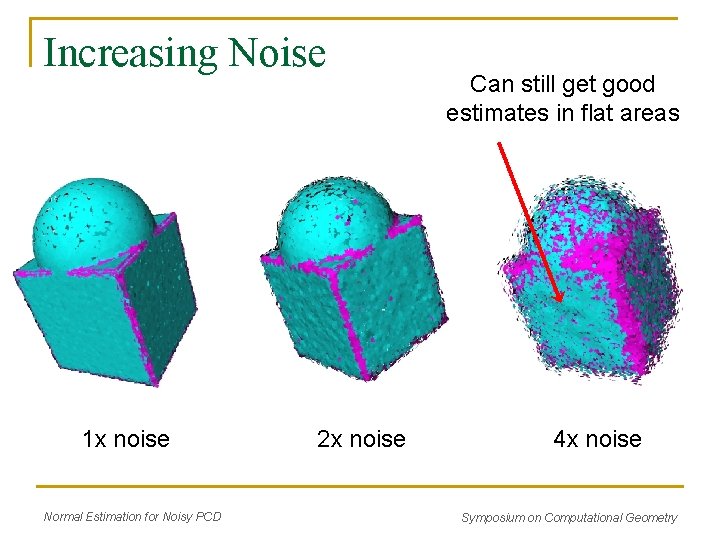
Increasing Noise 1 x noise Normal Estimation for Noisy PCD 2 x noise Can still get good estimates in flat areas 4 x noise Symposium on Computational Geometry

Future Work n n n How to find a suitable neighborhood size for good curvature estimation Find a better way for estimating c 1, c 2 Design of a sparse query data structure for quick extraction of normal, curvature, etc from PCDs Normal Estimation for Noisy PCD Symposium on Computational Geometry

Different Noise Distribution (same variance) uniform Normal Estimation for Noisy PCD gaussian Symposium on Computational Geometry

Result: phone 1 x noise Normal Estimation for Noisy PCD Symposium on Computational Geometry

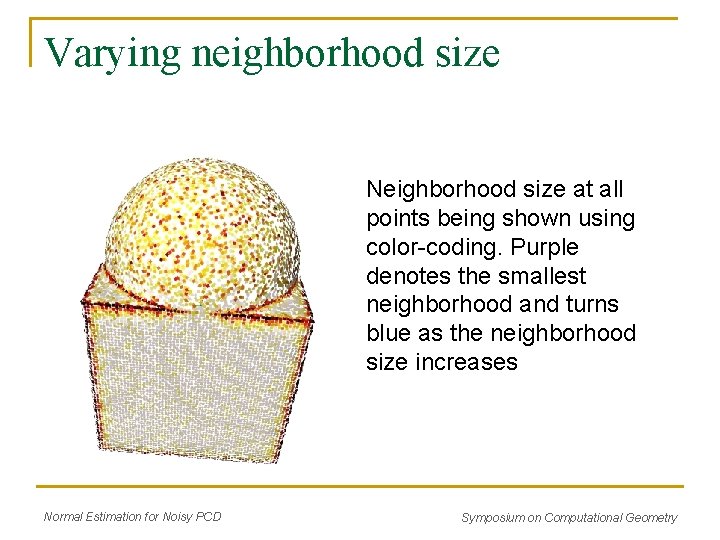
Varying neighborhood size Neighborhood size at all points being shown using color-coding. Purple denotes the smallest neighborhood and turns blue as the neighborhood size increases Normal Estimation for Noisy PCD Symposium on Computational Geometry