Estimating reconstruction uncertainties Dmitry Chirkin Outline 1 Calculation

Estimating reconstruction uncertainties Dmitry Chirkin

Outline 1. Calculation of uncertainties: limitation of the inverse Hessian (if the likelihood function is not based on the actual PDF) 2. Re-sampling techniques for uncertainty estimation: bootstrapping 3. Direct re-sampling approach 4. Some results: pull distributions (deviation from true value divided by the uncertainty estimate) 5. An alternative to iterative reconstruction

Common error analysis Uncertainties are often estimated by incrementing -2 * Log likelihood by 1: -2 ln. L = -2 ln. L 0 + Hij dxi dxj ~ 1 < dxi dxj > ~ Hij-1 The full equation Hij dxi dxj = 1 can be used to represent the uncertainty ellipse.

Estimating uncertainties our approximation to PDF Expand F near the global minimum x 0 for data set {n}: The new minimum for set {n} is determined by

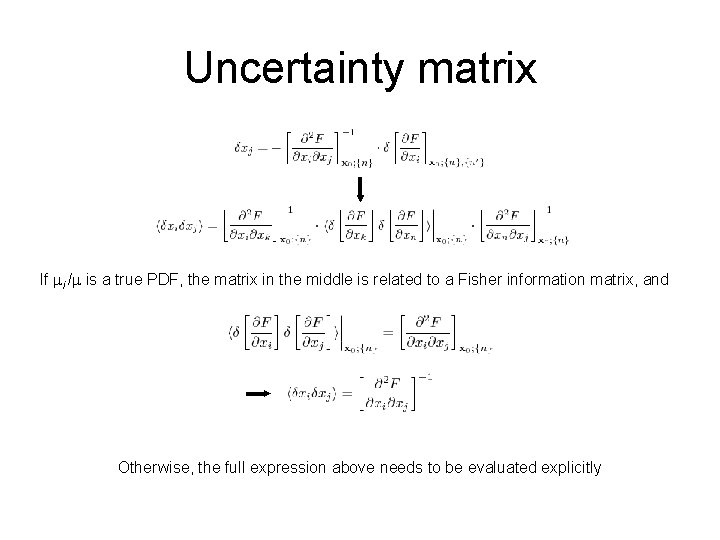
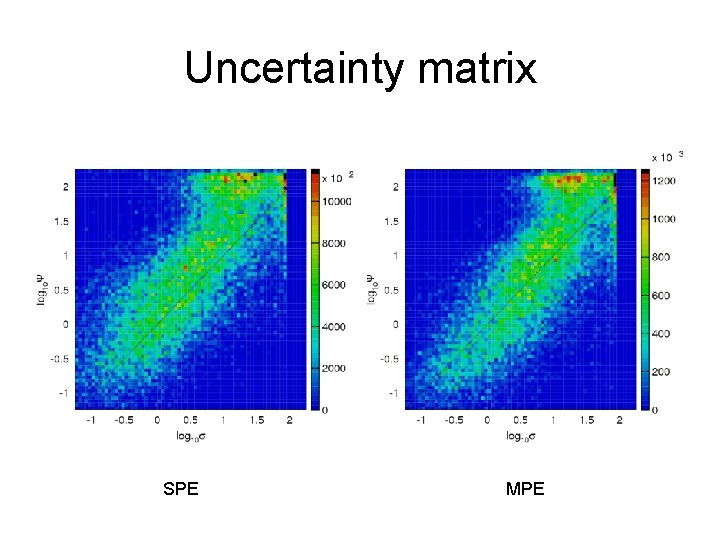
Uncertainty matrix If mi /m is a true PDF, the matrix in the middle is related to a Fisher information matrix, and Otherwise, the full expression above needs to be evaluated explicitly

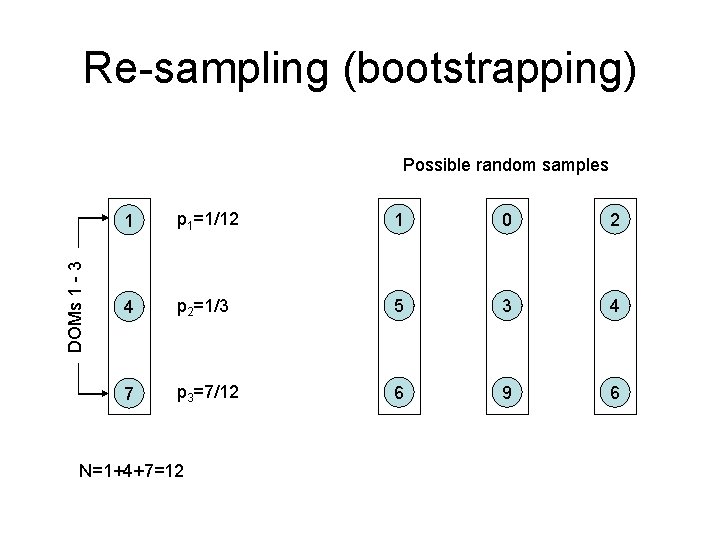
Variation matrix This can be computed if we can repeat (or re-simulate) the experiment many times. As an approximation we can assume ni /N are probabilities and re-draw (re-sample) the data set of N points many times (bootstrapped re-sampling technique). One can avoid re-creating the experiment many times using the properties of the multinomial distribution: e. g. , the variation of F simplifies to

Re-sampling (bootstrapping) DOMs 1 - 3 Possible random samples 1 p 1=1/12 1 0 2 4 p 2=1/3 5 3 4 7 p 3=7/12 6 9 6 N=1+4+7=12

Alternative/more precise approach Instead of expanding in the variation of {n}, the likelihood is re-expanded for each new set {n’}: This simplifies the calculation of interesting uncertainties, e. g. , s 50%.

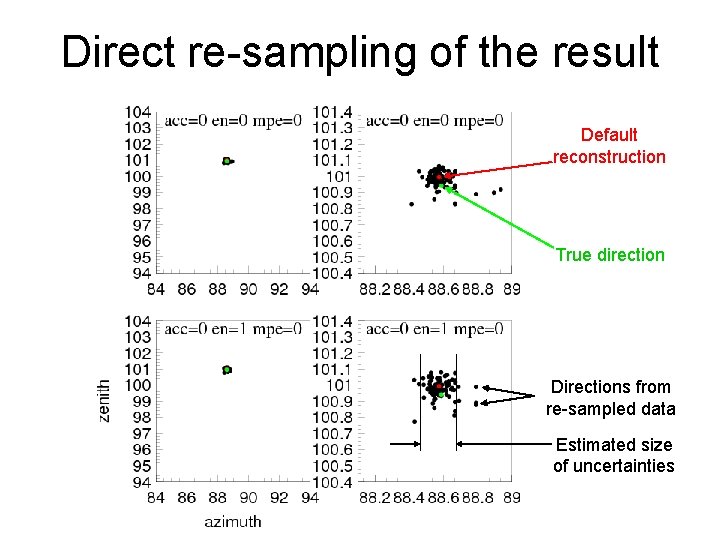
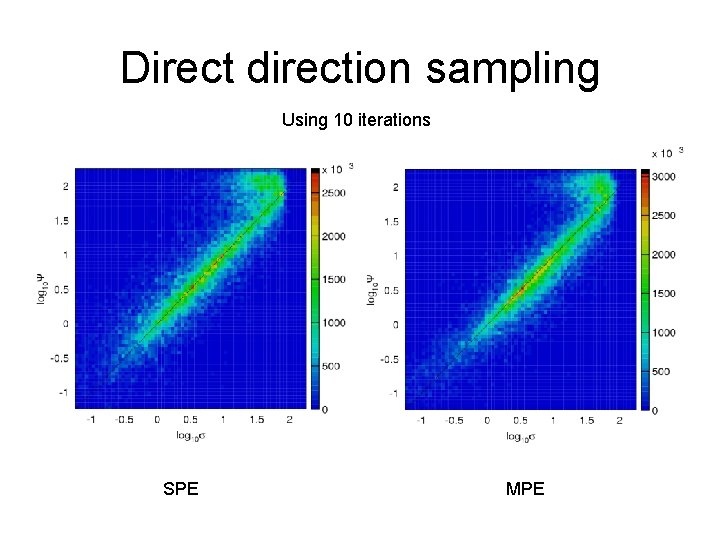
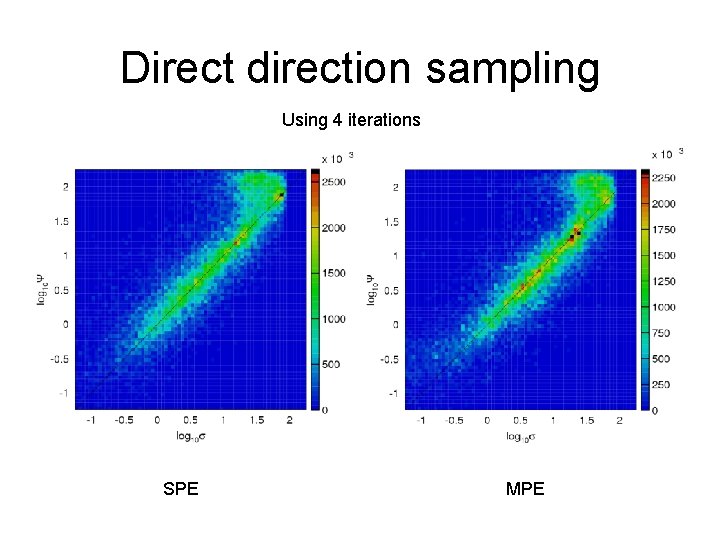
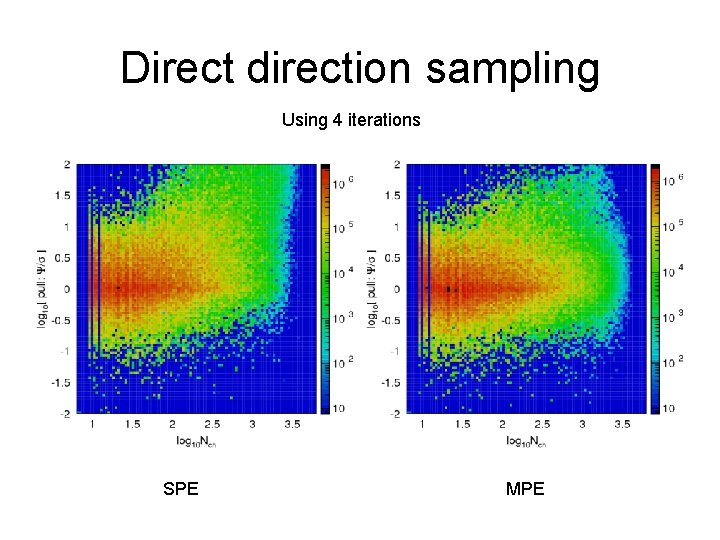
Direct re-sampling of the result Default reconstruction True direction Directions from re-sampled data Estimated size of uncertainties

Results

Uncertainty matrix SPE MPE

Direct direction sampling Using 10 iterations SPE MPE

Direct direction sampling Using 4 iterations SPE MPE

Direct direction sampling Using 4 iterations SPE MPE

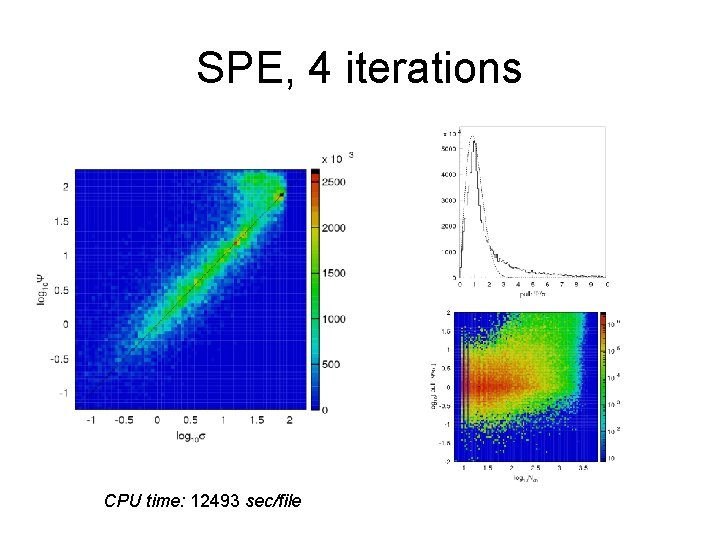
SPE, 4 iterations CPU time: 12493 sec/file

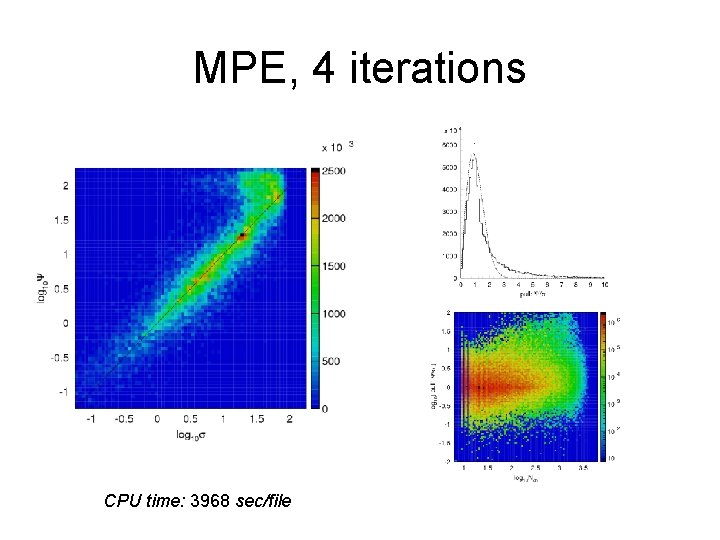
MPE, 4 iterations CPU time: 3968 sec/file

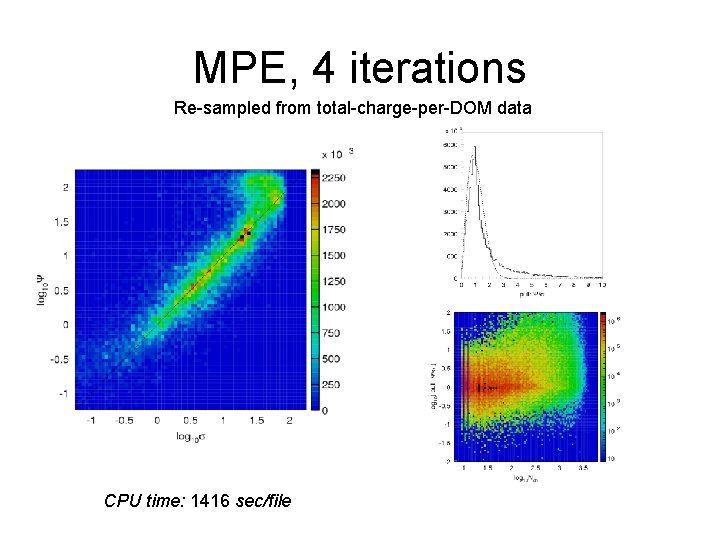
MPE, 4 iterations Re-sampled from total-charge-per-DOM data CPU time: 1416 sec/file

A problem The solution in the iterative approach was taken as the average of the iterations. It turns out that the solution obtained for the initial (not resampled) data is in closer agreement with the true direction. Thus, the uncertainty for such a solution is actually smaller than that predicted by the re-sampling method. I would expect the opposite: the re-sampling method should result in a under-estimate of the errors. this needs to be understood

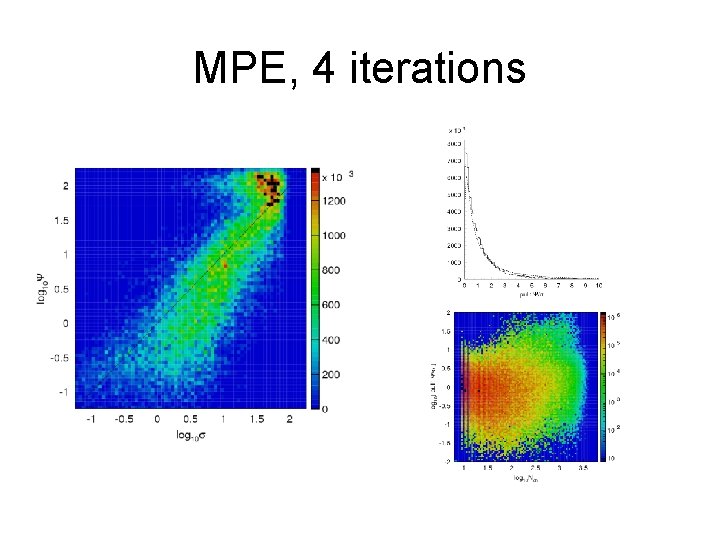
MPE, 4 iterations

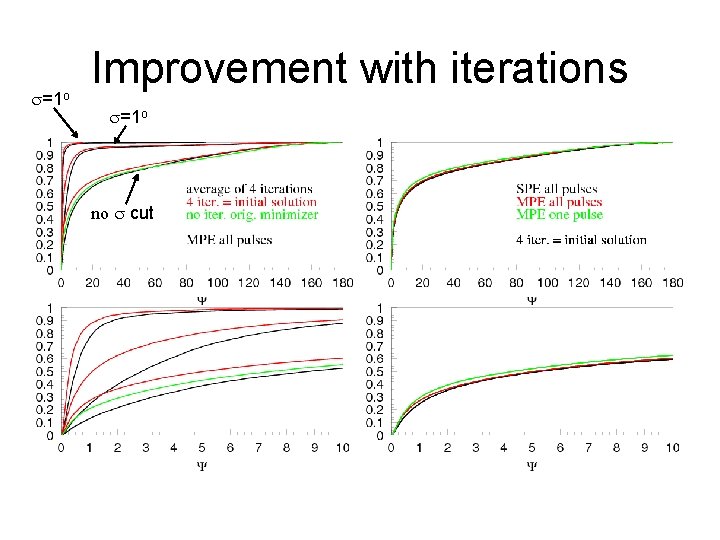
An intriguing observation Using the average of the iterations as the initial solution for the minimizer results in a substantial improvement of the reconstructed direction! With more iterations the precision of the eventual reconstructed track direction improves.

s=1 o Improvement with iterations s=1 o no s cut

Remarks • The “likelihood function” based on the approximation to the true PDF is not the true likelihood function uncertainties are not given by the width of –ln L • Bootstrapping re-sampling procedure results in a robust approximation to uncertainties in the reconstructed parameters. • Here only angular uncertainty was shown. The uncertainties of other parameters (e. g. , energy) can also be estimated using this approach. • Get the code estimating angular and energy proxy uncertainties from http: //code. icecube. wisc. edu/svn/projects/mue/branches/wreco/.