Estimating High Dimensional Covariance Matrix and Volatility Index

Estimating High Dimensional Covariance Matrix and Volatility Index by making Use of Factor Models Celine Sun R/Finance 2013 1

Outline • Introduction • Proposed estimation of covariance matrix: – Estimator 1: Factor-Model Based – Estimator 2: SVD based – Empirical testing results • Proposed volatility estimation: – Cross-section volatility (CSV) – Empirical Results • Conclusion 2

Two new estimators are proposed in this work: • We propose two new covariance matrix estimators : 1. Allow non-parametrically time-varying: Estimate the monthly realized covariance matrix using daily data 2. Allow full rank for N>T: – Using the factor model and SVD to estimate such that the covariance estimator is full rank – The new estimators are different from the commonly used estimators and approaches 3

Covariance matrix estimation based on FM (factor models) – We propose an estimation of covariance matrix, based on a statistical factor model with k factors (k < N). – Here, { } are the loadings, – { } are the regression errors. – Note: The estimator matrix is full rank. 4

Covariance matrix estimation based on SVD method – I propose the 2 nd estimation covariance matrix, based on SVD: – of Here, { } and { } are from the usual eigen decomposition of the Nx. N realized variance matrix, and having , with k < N. – { } = the remaining terms from reconstructing the return matrix by { } and { } 5

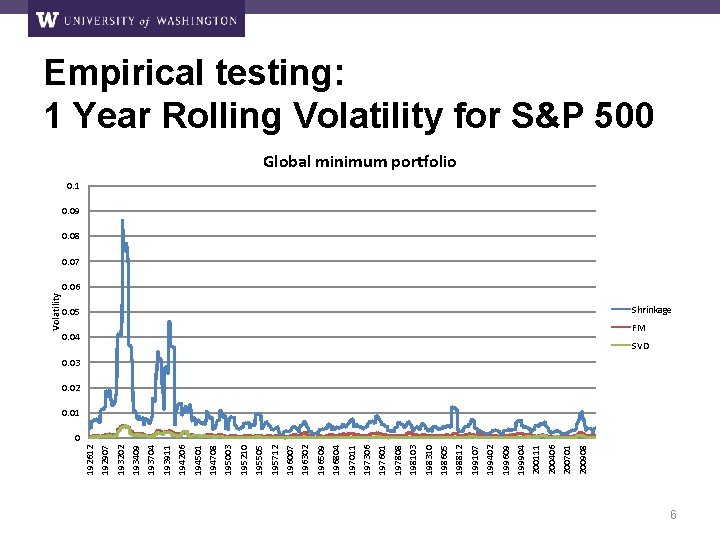
200908 200701 200406 200111 199904 199609 199402 199107 198812 198605 198310 198103 197808 197601 197306 197011 196804 196509 196302 196007 195712 195505 195210 195003 194708 194501 194206 193911 193704 193409 193202 192907 192612 Volatility Empirical testing: 1 Year Rolling Volatility for S&P 500 Global minimum portfolio 0. 1 0. 09 0. 08 0. 07 0. 06 0. 05 Shrinkage 0. 04 FM SVD 0. 03 0. 02 0. 01 0 6

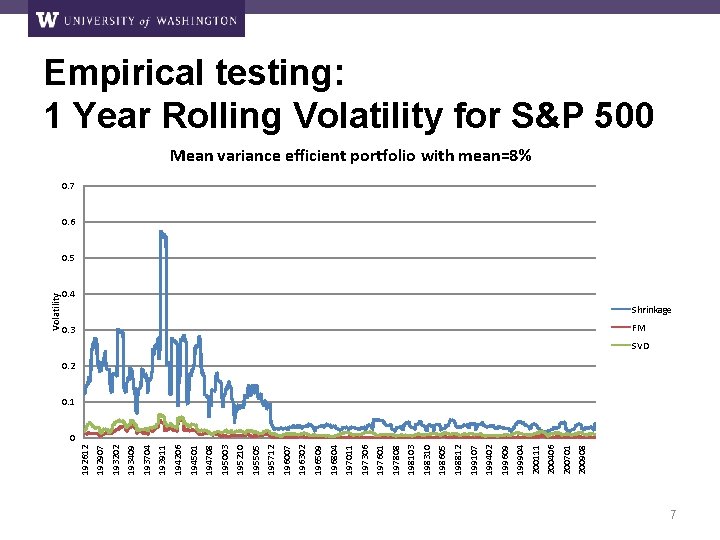
200908 200701 200406 200111 199904 199609 199402 199107 198812 198605 198310 198103 197808 197601 197306 197011 196804 196509 196302 196007 195712 195505 195210 195003 194708 194501 194206 193911 193704 193409 193202 192907 192612 Volatility Empirical testing: 1 Year Rolling Volatility for S&P 500 Mean variance efficient portfolio with mean=8% 0. 7 0. 6 0. 5 0. 4 Shrinkage 0. 3 FM SVD 0. 2 0. 1 0 7

Volatility Index • A number of drawbacks of current volatility index – Not based on actual stock returns – The index only available to liquid options – Only available at broad market level • Advantage of CSV – Observable at any frequency – Model-free – Available for every region, sector, and style of the equity markets – Don't need to resort option market 8

Cross-sectional volatility • Cross-sectional volatility (CSV) is defined as the standard deviation of a set of asset returns over a period. • The relationship between cross-sectional volatility, time-series volatility and average correlation is given by: 9

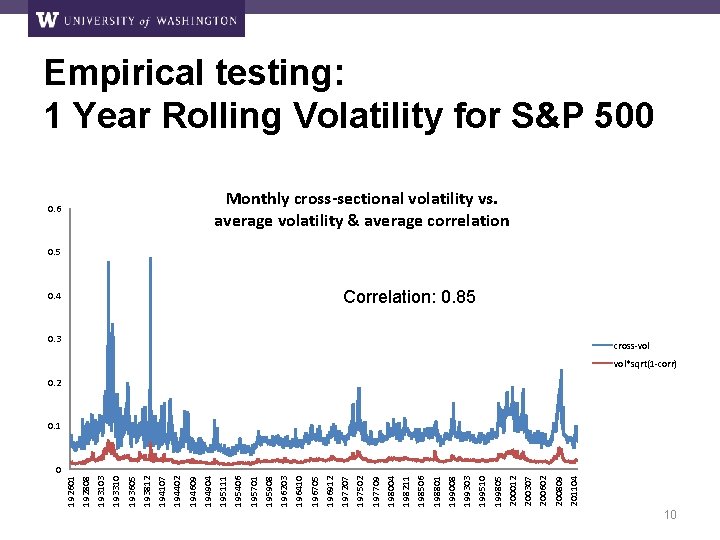
201104 200809 200602 200307 200012 199805 199510 199303 199008 198801 198506 198211 198004 197709 197502 0. 4 197207 196912 196705 196410 196203 195908 195701 195406 0. 6 195111 194904 194609 194402 194107 193812 193605 193310 193103 192808 192601 Empirical testing: 1 Year Rolling Volatility for S&P 500 Monthly cross-sectional volatility vs. average volatility & average correlation 0. 5 Correlation: 0. 85 0. 3 cross-vol vol*sqrt(1 -corr) 0. 2 0. 1 0 10

Decomposing Cross-Sectional Volatility • Apply the factor model on return • The change of beta is more persistent • Cross-sectional volatility of the specific return is a proxy for the future volatility • The correlation between VIX and CSV of specific return is 0. 62. 11

Conclusion • Constructed covariance matrix estimators which are full rank • The portfolios constructed based on my estimators have lower volatility • Applying factor model structure to CSV gives us a good estimation of the volatility. • It could be used at any frequency and at any set of stocks 12