Estadstica Captulo 4 2 PROBABILIDAD CONDICIONAL 3 2007

Estadística Capítulo 4. 2 PROBABILIDAD CONDICIONAL 3 -2007 1

Probabilidad Condicional En la probabilidad simple se tiene una muestra y en ese entorno de hacen todas las descripciones probabilísticas. Existen situaciones en las cuales se tiene la muestra; pero, de estudios previos se han obtenidos resultados que sirven de base para obtener nuevos resultados; a esto se le llama “probabilidad condicional” 3 -2007 2

Probabilidad Condicional La probabilidad condicional de un evento A dado que se tiene previamente un evento B es Es decir, se calcula de probabilidad conjunta de ambos eventos y el resultado se divide entre la probabilidad de B que es el evento que resultó. 3 -2007 3
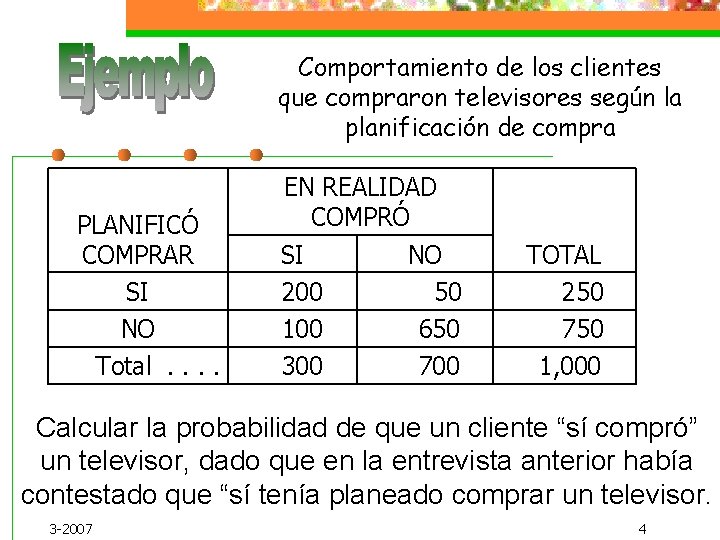
Comportamiento de los clientes que compraron televisores según la planificación de compra PLANIFICÓ COMPRAR SI NO Total. . EN REALIDAD COMPRÓ SI NO 200 50 100 650 300 700 TOTAL 250 750 1, 000 Calcular la probabilidad de que un cliente “sí compró” un televisor, dado que en la entrevista anterior había contestado que “sí tenía planeado comprar un televisor. 3 -2007 4

1. Probabilidad de que si compró un tv, dado que haya planeado comprar un televisor en la entrevista anterior Planteamiento Sí compró un TV Sí planeó comprar un TV 3 -2007 : : A B 5

* Los clientes que planearon comprar un TV y efectivamente sí lo compraron son 200 * Los clientes que en la entrevista anterior dijeron que sí estaban planificando comprar un televisor son 250. 3 -2007 6

El 80% de los clientes que planificaron comprar hace doce meses, sí compraron el televisor de pantalla plana. 3 -2007 7

Independencia Estadística Si en una investigación, una de las preguntas es base para la respuesta de otra de ellas, se establece una dependencia de la segunda con respecto a la primera. Por lo tanto, si una de las preguntas no afecta en nada la respuesta de la otra; se dice que hay independencia estadística. 3 -2007 8

Independencia Estadística La independencia estadística se puede definir como: Entonces, dos eventos A y B son estadísticamente independientes si y solo sí P(A/B)=P(A) 3 -2007 9
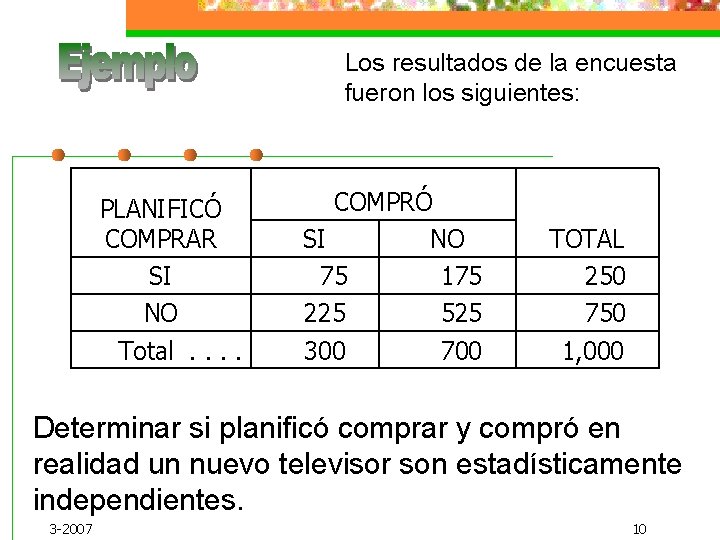
Los resultados de la encuesta fueron los siguientes: PLANIFICÓ COMPRAR SI NO Total. . COMPRÓ SI NO 75 175 225 525 300 700 TOTAL 250 750 1, 000 Determinar si planificó comprar y compró en realidad un nuevo televisor son estadísticamente independientes. 3 -2007 10
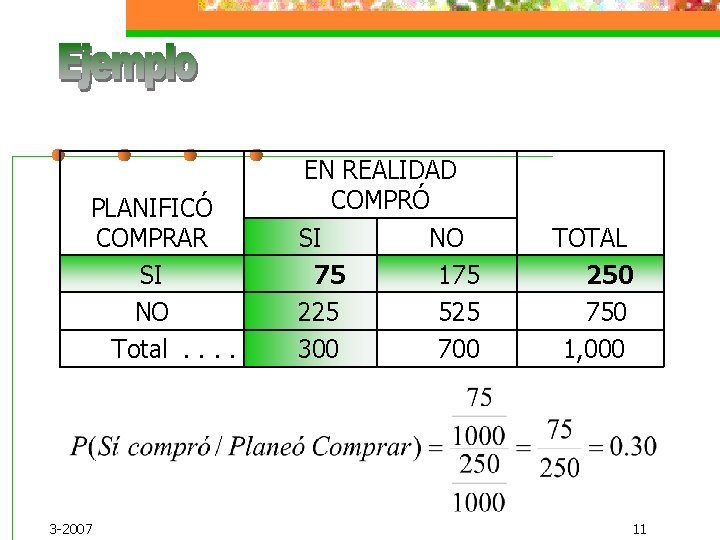
PLANIFICÓ COMPRAR SI NO Total. . 3 -2007 EN REALIDAD COMPRÓ SI NO 75 175 225 525 300 700 TOTAL 250 750 1, 000 11
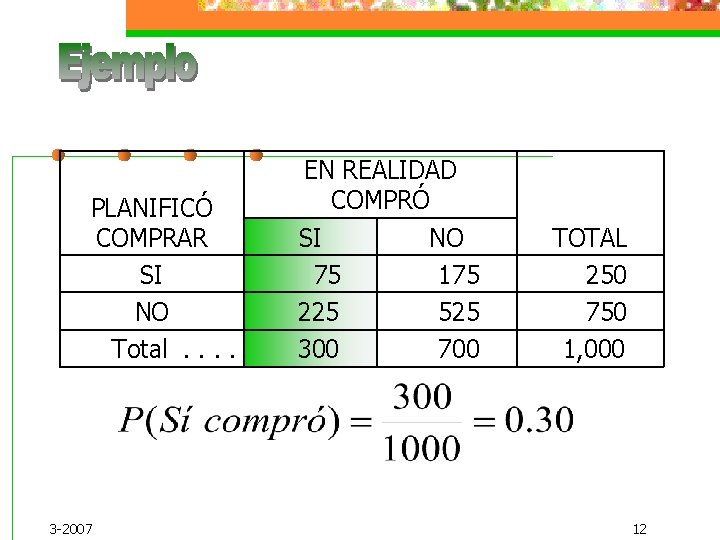
PLANIFICÓ COMPRAR SI NO Total. . 3 -2007 EN REALIDAD COMPRÓ SI NO 75 175 225 525 300 700 TOTAL 250 750 1, 000 12

Ambos resultados son iguales, el hecho de haber Planeado comprar no incidió en el resultado. Los eventos son independientes. 3 -2007 13

Regla de multiplicación La regla de la multiplicación resulta de la Probabilidad condicional. Es otra forma de calcular la probabilidad conjunta 3 -2007 14

Suponga que su sobrino tiene una bolsa con 26 mables, de los cuales 10 son rojos, 8 son amarillos, 5 son azules y 3 son verdes. Usted quiere que su sobrino le regale dos mables. ¿Qué probabilidad tiene que ambos mables sean rojos? . Lo que se busca es que el primero sea rojo y el segundo también sea rojo. 3 -2007 15

Primero se calculará la probabilidad de que el primer mable que regale su sobrino sea rojo. Segundo se calculará la probabilidad de que el segundo mable que regale su sobrino sea rojo, siendo que ya le dio el primero y fue rojo. 3 -2007 16

La probabilidad de que sean rojos ambos mables se formula como: 3 -2007 17

Su sobrino tiene una bolsa con 26 mables, de los cuales 10 son rojos, 8 son amarillos, 5 son azules y 3 son verdes. Usted quiere que su sobrino le regale dos mables. ¿Qué probabilidad tiene que uno sea azul y el otro sea rojo? . Lo que se busca es que el primero sea rojo y el segundo sea azul o que el primero sea azul y el segundo sea rojo. 3 -2007 18

3 -2007 19

REEMPLAZOS Cada vez que se extrae un elemento de la muestra, ésta se reduce; podemos decir que el muestreo es sin reemplazo. Cada vez que se extrae un elemento de la muestra y una vez marcado se devuelve a su sitio en la muestra, se dice que el muestreo es con reemplazo. En el ejemplo anterior se utilizó el muestreo sin reemplazo, cada vez que un mable es extraído no se vuelve a colocar en la bolsa. 3 -2007 20

Suponga que su sobrino sólo le va a enseñar los maules que tiene en la bolsa; son 26 mables en total, de los cuales 10 son rojos, 8 son amarillos, 5 son azules y 3 son verdes. Usted quiere que su sobrino le enseñe dos mables. ¿Qué probabilidad tiene que ambos mables sean rojos? . Lo que se busca es que el primero sea rojo y el segundo también sea rojo. 3 -2007 21

Primero se calculará la probabilidad de que el primer mable que enseñe su sobrino sea rojo. Devolver el mable a la bolsa. Ahora se calculará la probabilidad de que el segundo mable que le enseñe su sobrino sea rojo, siendo que ya le enseñó el primero y fue rojo. 3 -2007 22

3 -2007 23
Suponga que su sobrino sólo le va a enseñar los mables que tiene en la bolsa; son 26 mables en total, de los cuales 10 son rojos, 8 son amarillos, 5 son azules y 3 son verdes. Usted quiere que su sobrino le enseñe dos mables. ¿Qué probabilidad tiene que uno sea azul y el otro sea rojo? . 3 -2007 24

Puede ser que suceda lo siguiente: * El primero que le enseñe es azul y el segundo rojo * El primero que le enseña sea rojo y el segundo azul 3 -2007 25

La probabilidad que se anda buscando es la siguiente: Primero se resuelve la probabilidad de que le enseñe primero el azul y luego el rojo. Segundo: Se va a resolver la probabilidad de que le enseñe primero el rojo y luego el azul. 3 -2007 26

3 -2007 27

3 -2007 28

3 -2007 29

Fin del capítulo 4. 2 Continúa 4. 5 3 -2007 30
- Slides: 30