Establishing Chart Datum Across the Bay of Fundy

Establishing Chart Datum Across the Bay of Fundy using Virtual Tide Gauges Nathan C. Wardwell Masters Student Center for Coastal and Ocean Mapping and UNH Department of Earth Sciences 1

Outline • Problem – Obtaining complete tidal information along a transect • Method – Extract Virtual Tide Gauge information along an often repeated ferry track • Results – Virtual Tide Gauge harmonic constituents and reference surfaces • Conclusions 2

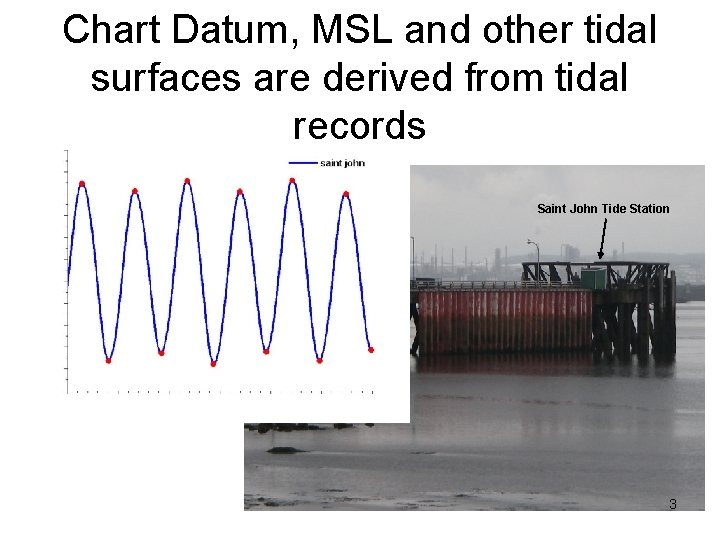
Chart Datum, MSL and other tidal surfaces are derived from tidal records Saint John Tide Station 3

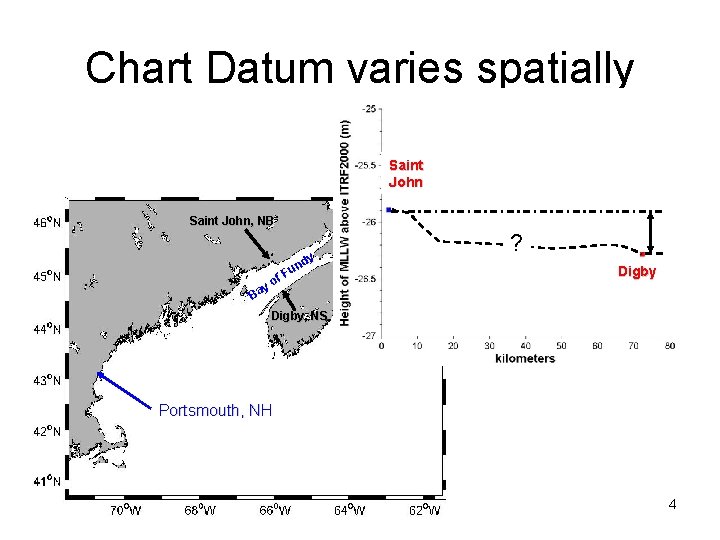
Chart Datum varies spatially Saint John, NB dy f B o ay n Fu ? 39 cm Digby, NS Portsmouth, NH 4

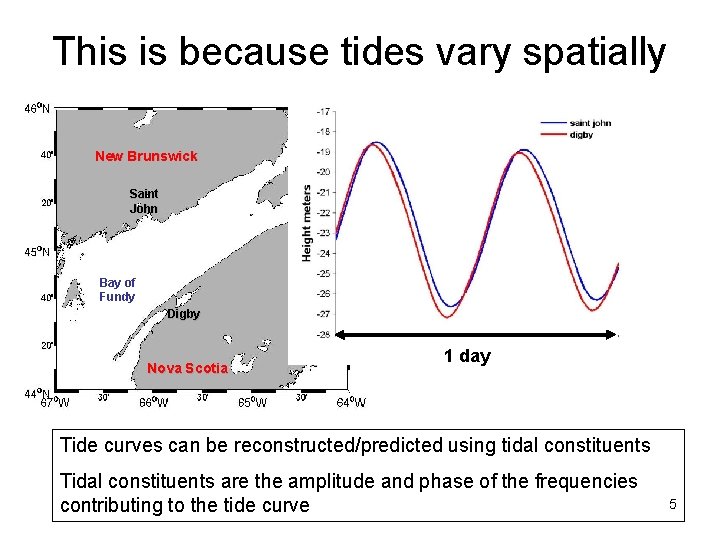
This is because tides vary spatially New Brunswick Saint John Bay of Fundy Digby Nova Scotia 1 day Tide curves can be reconstructed/predicted using tidal constituents Tidal constituents are the amplitude and phase of the frequencies contributing to the tide curve 5

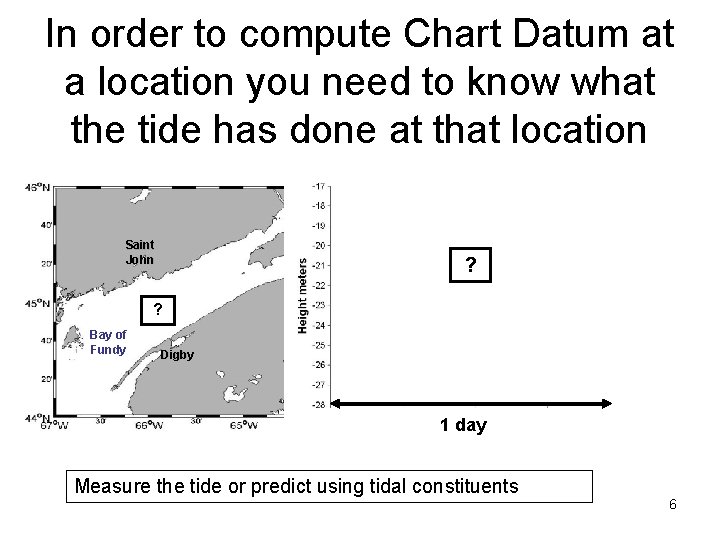
In order to compute Chart Datum at a location you need to know what the tide has done at that location Saint John ? ? Bay of Fundy Digby 1 day Measure the tide or predict using tidal constituents 6

Site-specific offshore tidal sensors • GPS buoy http: //www. ehs. unu. edu/image. php? id=149&ver=600 – Provides water levels with respect to the ellipsoid • Bottom mounted pressure gauge – Provides “water level” fluctuations – Retrieving data can be problematic 7

A non site-specific option is to use a “moving GPS buoy” New Brunswick Saint John Bay of Fundy Digby Nova Scotia Use ferry as virtual tide gauge to simulate a string of GPS buoys 8

Research used data provided by UNB and USM funded by ONR GPS Antenna • GPS base stations established in – Saint John, NB – Digby, NS • Two sets of single baseline PPK solutions computed in 2005 at UNB • No corrections for – Roll – Pitch – Heave – Settlement and Squat • Applied static vertical offset to reduce heights from the antenna to the water level Met Station Installed in Nov 2003 and removed in Dec 2004 9

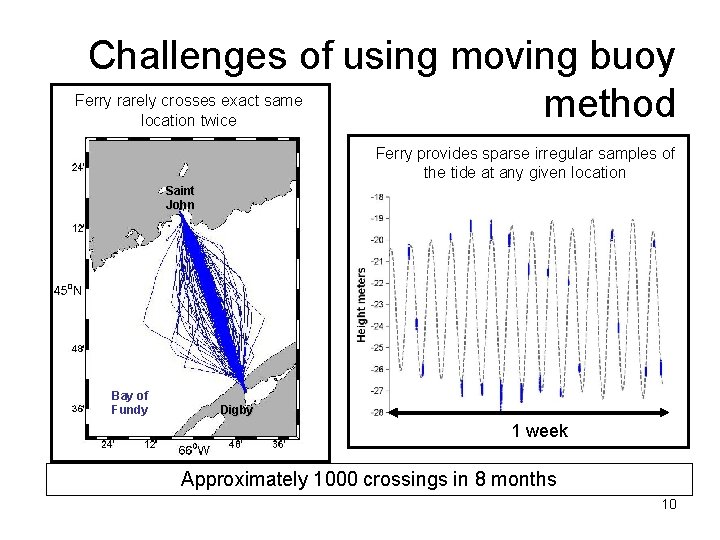
Challenges of using moving buoy method Ferry rarely crosses exact same location twice Ferry provides sparse irregular samples of the tide at any given location Saint John Bay of Fundy Digby 1 week Approximately 1000 crossings in 8 months 10

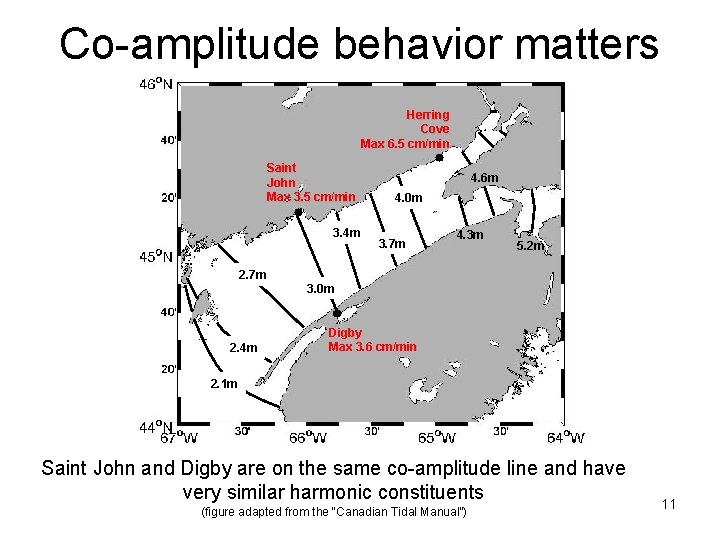
Co-amplitude behavior matters Herring Cove Max 6. 5 cm/min Saint John Max 3. 5 cm/min 3. 4 m 4. 6 m 4. 0 m 3. 7 m 4. 3 m 5. 2 m 2. 7 m 3. 0 m 2. 4 m Digby Max 3. 6 cm/min 2. 1 m Saint John and Digby are on the same co-amplitude line and have very similar harmonic constituents (figure adapted from the “Canadian Tidal Manual”) 11

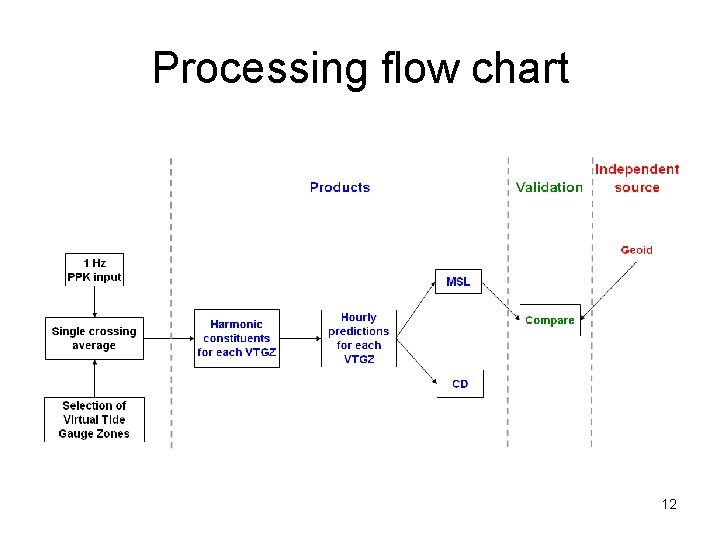
Processing flow chart 12

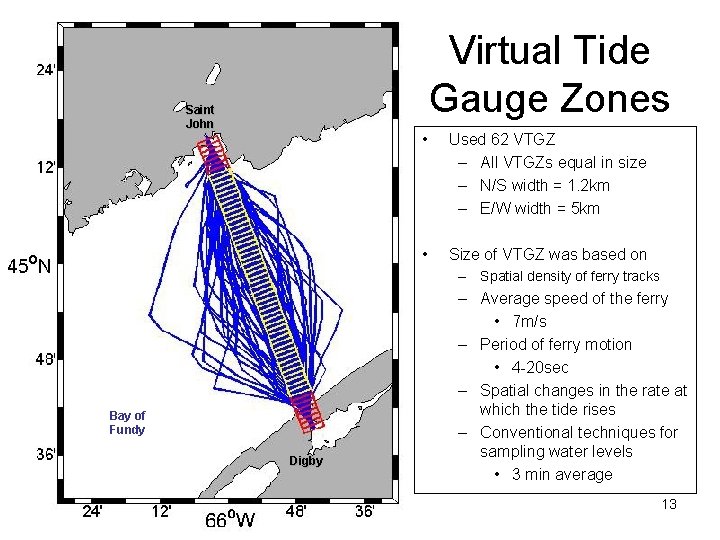
Virtual Tide Gauge Zones Saint John • Used 62 VTGZ – All VTGZs equal in size – N/S width = 1. 2 km – E/W width = 5 km • Size of VTGZ was based on – Spatial density of ferry tracks Bay of Fundy Digby – Average speed of the ferry • 7 m/s – Period of ferry motion • 4 -20 sec – Spatial changes in the rate at which the tide rises – Conventional techniques for sampling water levels • 3 min average 13

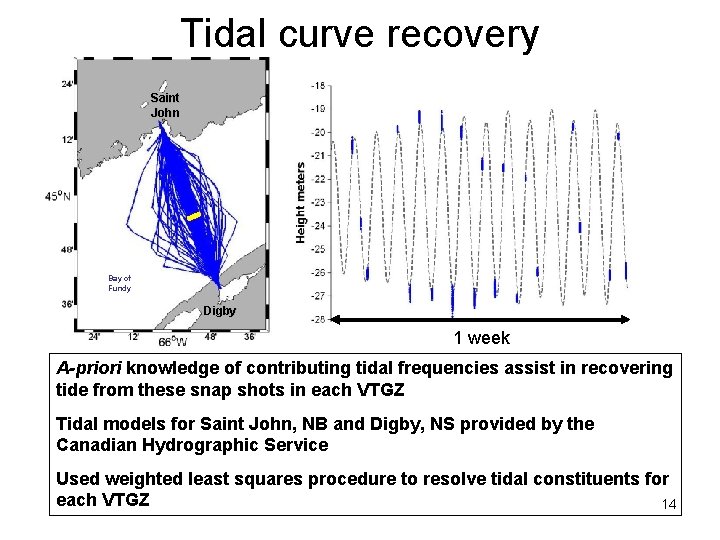
Tidal curve recovery Saint John Bay of Fundy Digby 1 week A-priori knowledge of contributing tidal frequencies assist in recovering tide from these snap shots in each VTGZ Tidal models for Saint John, NB and Digby, NS provided by the Canadian Hydrographic Service Used weighted least squares procedure to resolve tidal constituents for each VTGZ 14

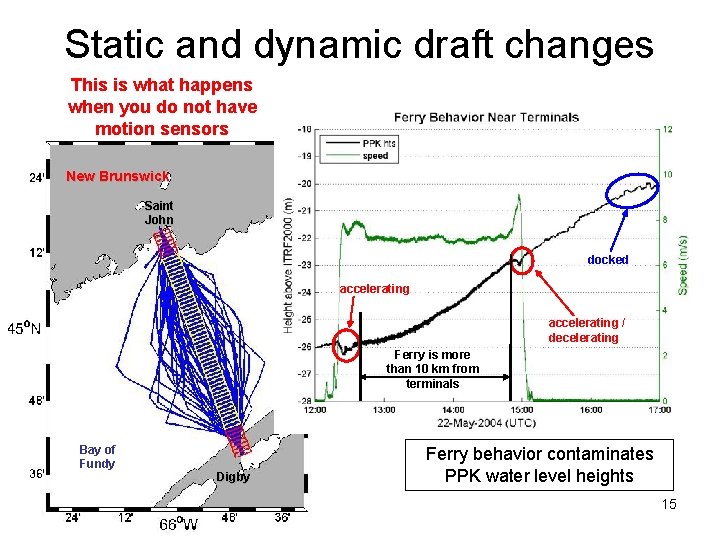
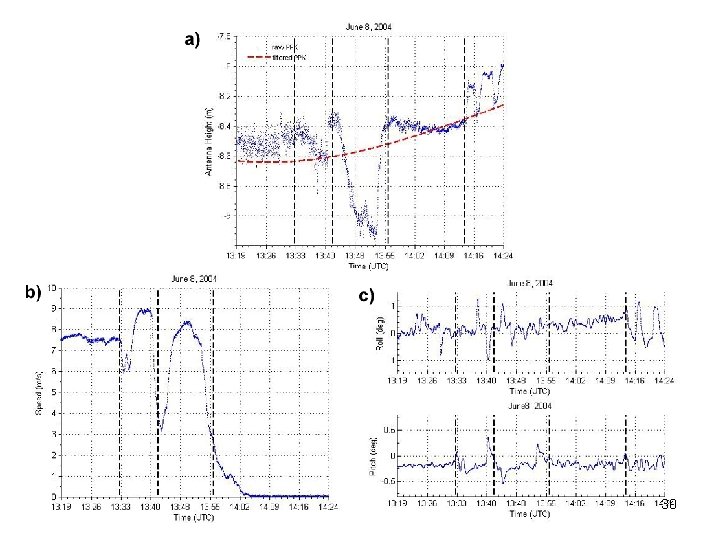
Static and dynamic draft changes This is what happens when you do not have motion sensors New Brunswick Saint John docked accelerating / decelerating Ferry is more than 10 km from terminals Bay of Fundy Digby Ferry behavior contaminates PPK water level heights 15

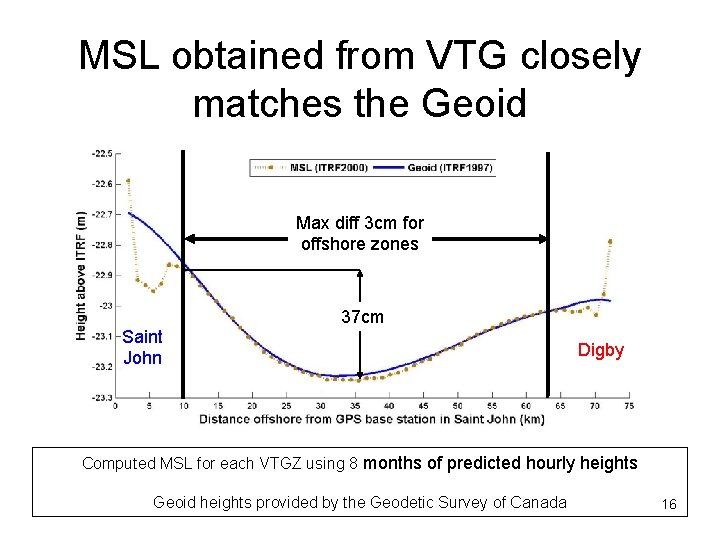
MSL obtained from VTG closely matches the Geoid Max diff 3 cm for offshore zones Saint John 37 cm Digby Computed MSL for each VTGZ using 8 months of predicted hourly heights Geoid heights provided by the Geodetic Survey of Canada 16

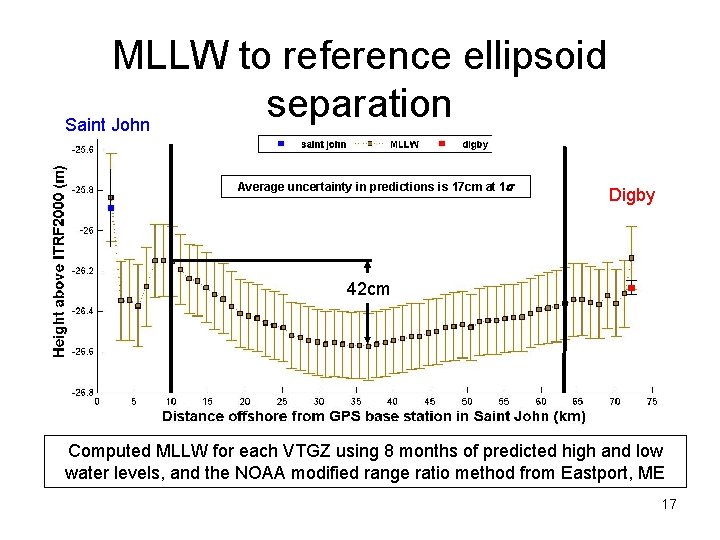
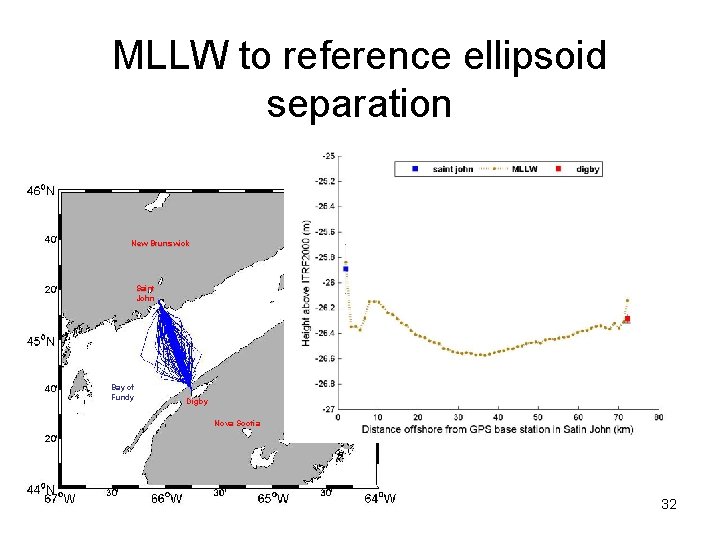
MLLW to reference ellipsoid separation Saint John Average uncertainty in predictions is 17 cm at 1 s Digby 42 cm Computed MLLW for each VTGZ using 8 months of predicted high and low water levels, and the NOAA modified range ratio method from Eastport, ME 17

Conclusions • The Virtual Tide Gauge method works, as demonstrated by the agreement between MSL and the Geoid • In the middle of the bay MLLW is 30 cm lower than in Digby and 70 cm lower than in Saint John • Static and dynamic draft changes due to ferry maneuvers contaminate the PPK water level heights, which in turn bias the harmonic analysis • Transects between terminals with dissimilar tidal characteristics will be more challenging for this method 18

Thank you • • • NOAA grant NA 05 NOS 4001153 James V. Gardner (Committee chair) David E. Wells Lloyd C. Huff Semme J. Dijkstra Entire CCOM community 19

Questions? 20

21

Recommendations • Deploy a GPS Buoy in one of the Virtual Tide Gauge Zones to validate the MLLW heights 22

Tide curve recovery New Brunswick Saint John Bay of Fundy Digby Nova Scotia A-priori knowledge of contributing tidal frequencies assist in recovering tide from these snap shots CHS tide station located at Saint John, NB and Digby, NS 23

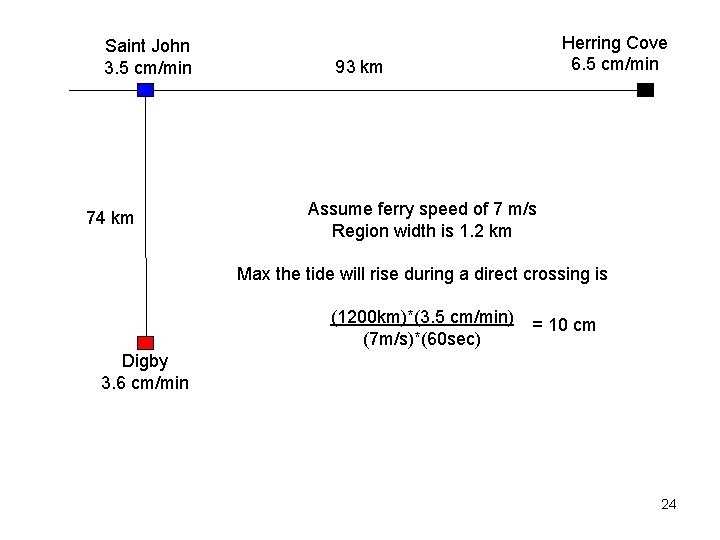
Saint John 3. 5 cm/min 74 km Herring Cove 6. 5 cm/min 93 km Assume ferry speed of 7 m/s Region width is 1. 2 km Max the tide will rise during a direct crossing is (1200 km)*(3. 5 cm/min) (7 m/s)*(60 sec) = 10 cm Digby 3. 6 cm/min 24

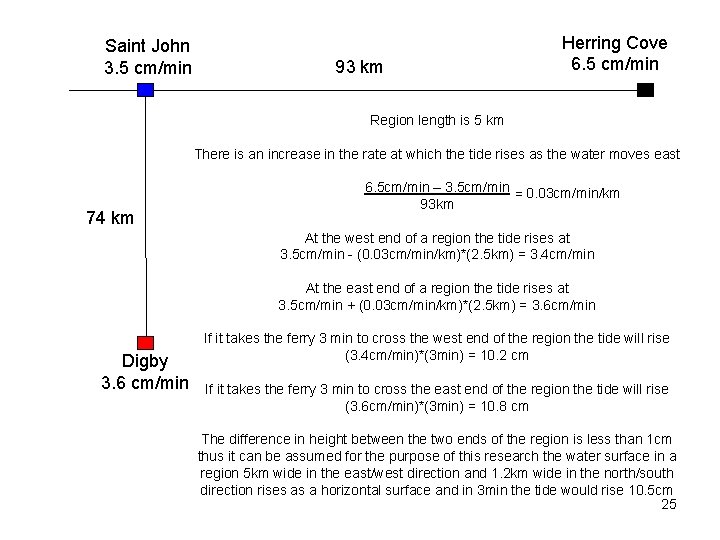
Saint John 3. 5 cm/min 93 km Herring Cove 6. 5 cm/min Region length is 5 km There is an increase in the rate at which the tide rises as the water moves east 74 km 6. 5 cm/min – 3. 5 cm/min = 0. 03 cm/min/km 93 km At the west end of a region the tide rises at 3. 5 cm/min - (0. 03 cm/min/km)*(2. 5 km) = 3. 4 cm/min At the east end of a region the tide rises at 3. 5 cm/min + (0. 03 cm/min/km)*(2. 5 km) = 3. 6 cm/min Digby 3. 6 cm/min If it takes the ferry 3 min to cross the west end of the region the tide will rise (3. 4 cm/min)*(3 min) = 10. 2 cm If it takes the ferry 3 min to cross the east end of the region the tide will rise (3. 6 cm/min)*(3 min) = 10. 8 cm The difference in height between the two ends of the region is less than 1 cm thus it can be assumed for the purpose of this research the water surface in a region 5 km wide in the east/west direction and 1. 2 km wide in the north/south direction rises as a horizontal surface and in 3 min the tide would rise 10. 5 cm 25

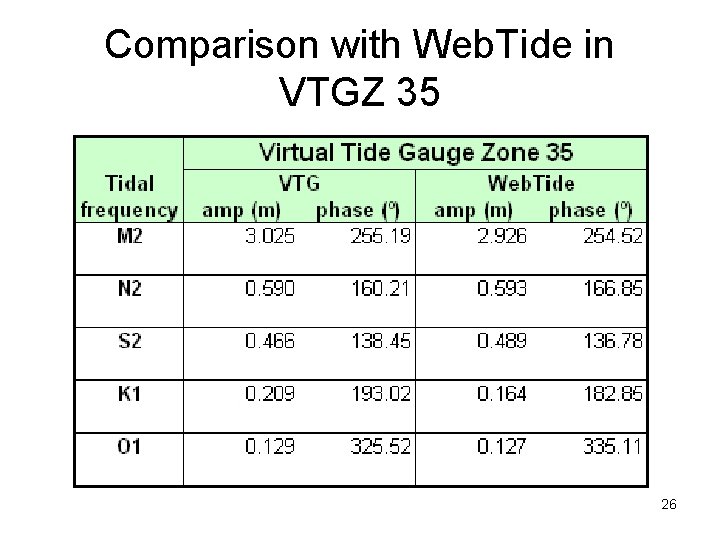
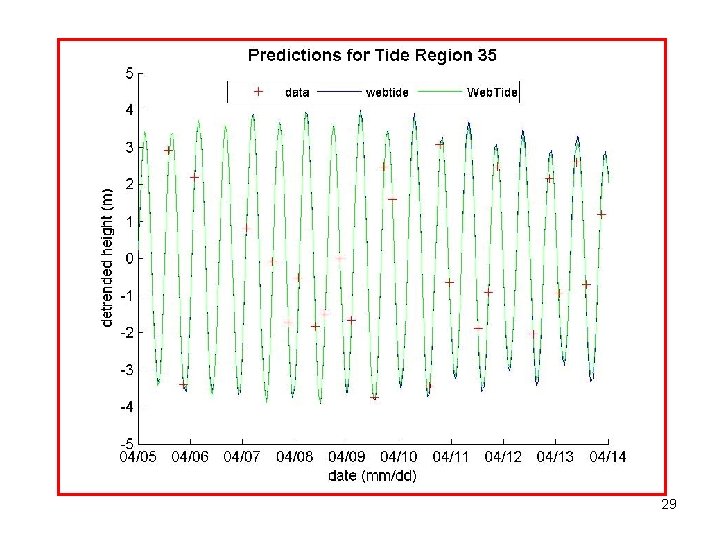
Comparison with Web. Tide in VTGZ 35 26

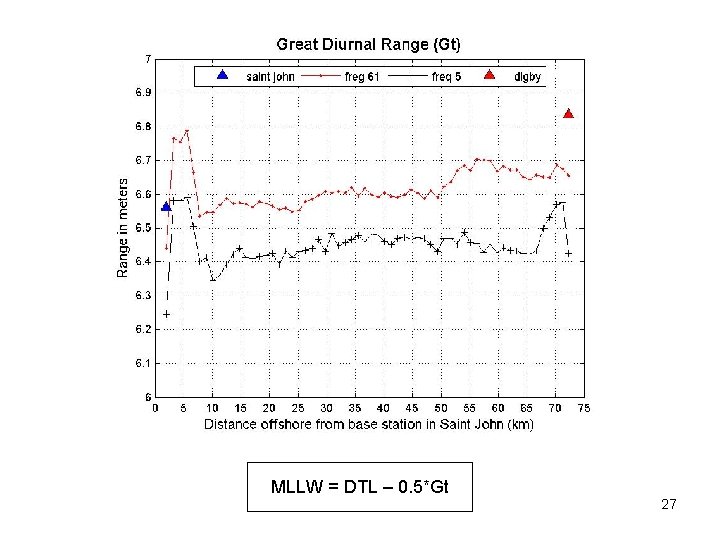
MLLW = DTL – 0. 5*Gt 27

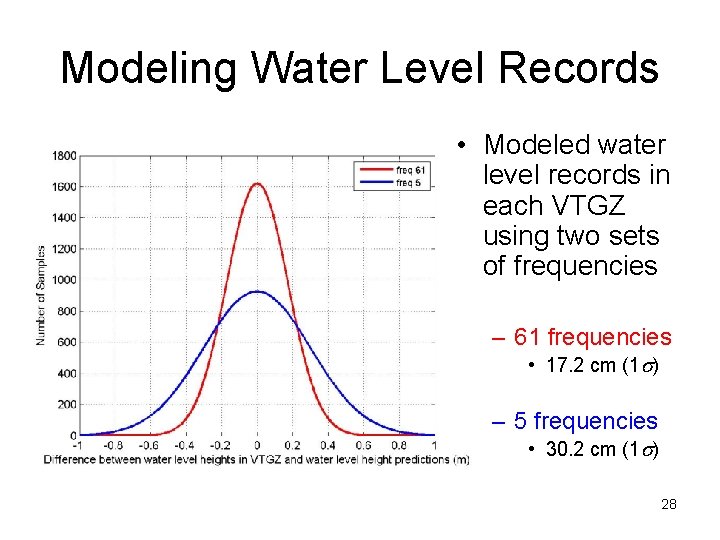
Modeling Water Level Records • Modeled water level records in each VTGZ using two sets of frequencies – 61 frequencies • 17. 2 cm (1 s) – 5 frequencies • 30. 2 cm (1 s) 28

29

30

Contribution Provide a low-cost efficient method for contributing to the development of a seamless datum. There a lot of scheduled ferry routes! Ferry Routes in Boston Harbor http: //www. mbta. com/schedules_and_maps/boats/ 31 http: //www. dot. state. ak. us/amhs/Travel. Options/Routes/index. html

MLLW to reference ellipsoid separation New Brunswick Saint John Bay of Fundy Digby Nova Scotia 32

Tidal Datums • Tabulate 8 months of monthly means – MSL – MLLW • Reduce and Correct to 1983 -2001 NTDE using Eastport, ME as control • Followed techniques described in “Computations Techniques for Tidal Datums Handbook” (NOAA Special Publication NOS CO-OPS 2) • Compared MSL-Ellipsoid separation to Geoid-Ellipsoid separation – Geoid-Ellipsoid separation obtained from Natural Resources Canada transformation software GPS-Hv 2. 0 • Compared offshore MLLW heights to MLLW heights measured on shore 33

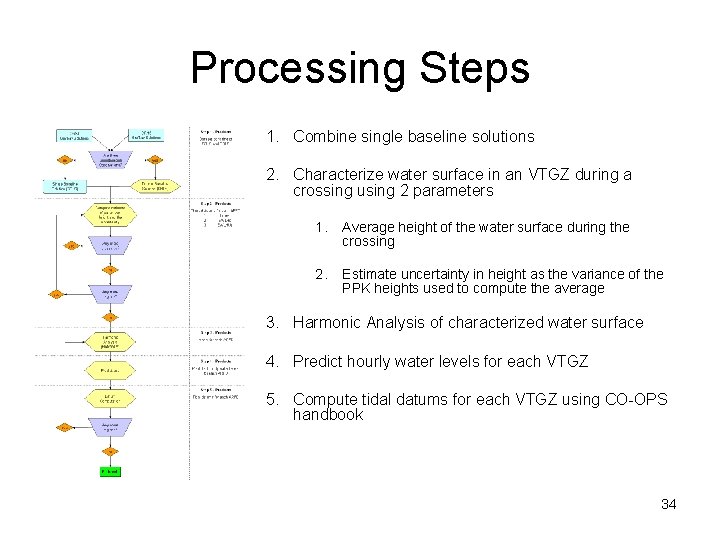
Processing Steps 1. Combine single baseline solutions 2. Characterize water surface in an VTGZ during a crossing using 2 parameters 1. Average height of the water surface during the crossing 2. Estimate uncertainty in height as the variance of the PPK heights used to compute the average 3. Harmonic Analysis of characterized water surface 4. Predict hourly water levels for each VTGZ 5. Compute tidal datums for each VTGZ using CO-OPS handbook 34

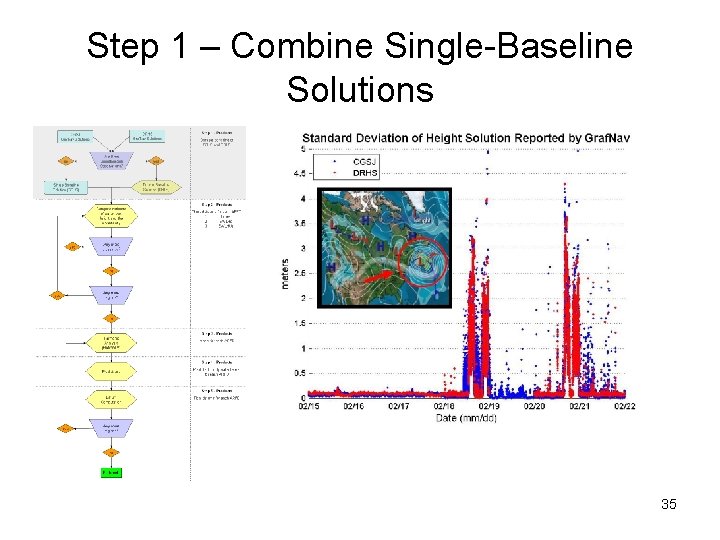
Step 1 – Combine Single-Baseline Solutions 35

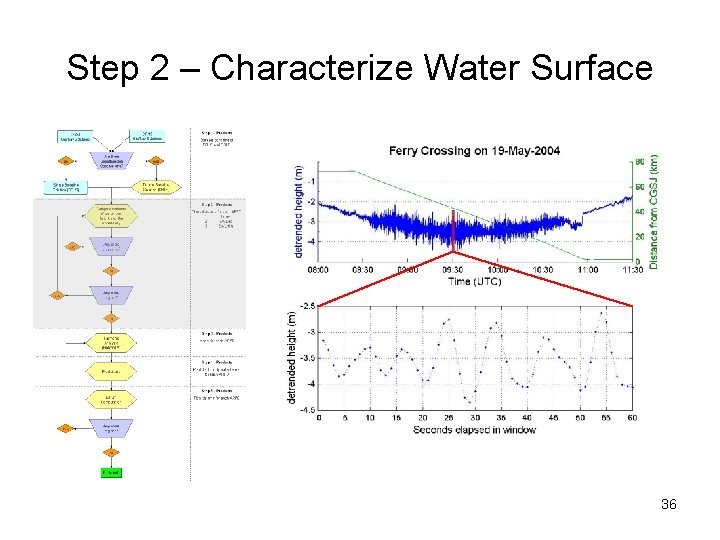
Step 2 – Characterize Water Surface 36

37

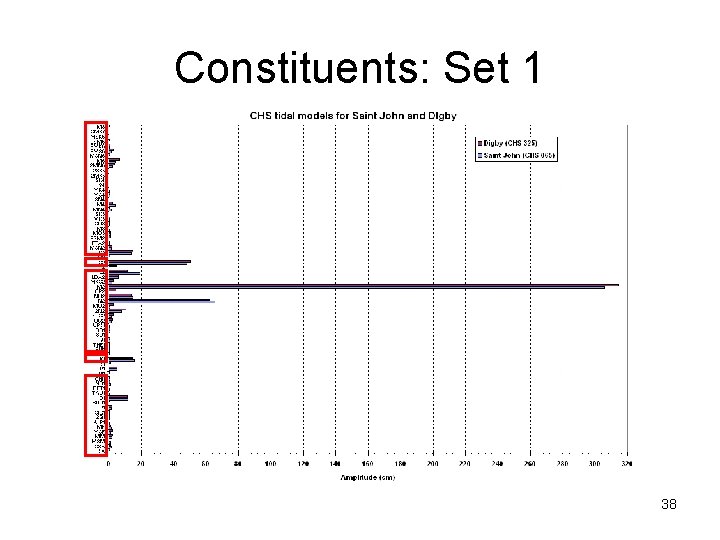
Constituents: Set 1 38

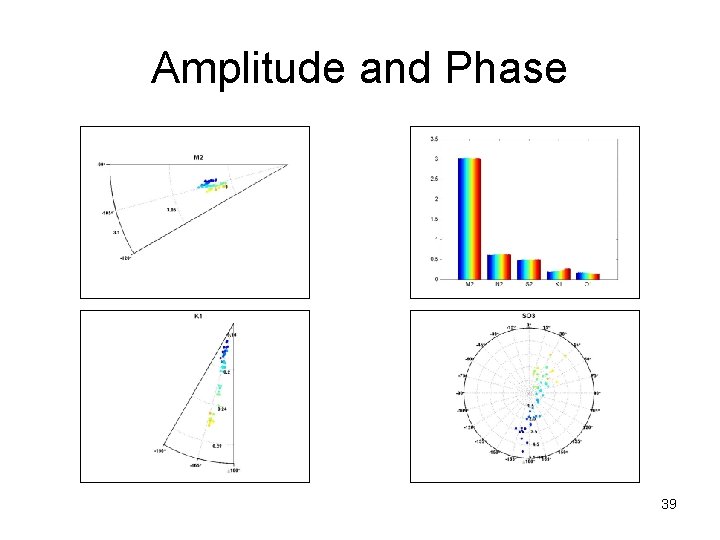
Amplitude and Phase 39

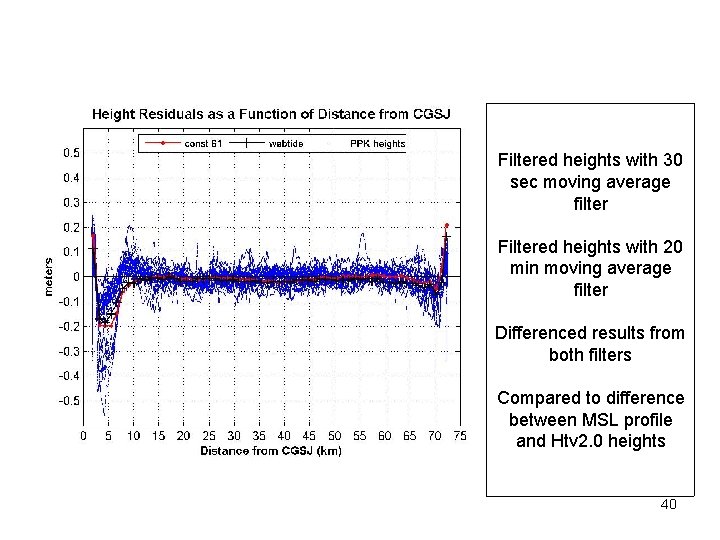
Filtered heights with 30 sec moving average filter Filtered heights with 20 min moving average filter Differenced results from both filters Compared to difference between MSL profile and Htv 2. 0 heights 40

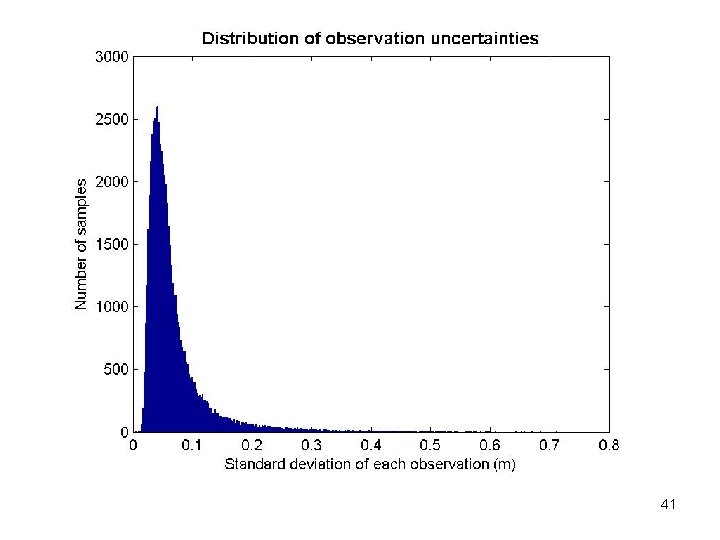
41

Tidal model • Two set of constituents – Set 1: nk = 61 – Set 2: nk = 5 • Used Weighted Least Squares Procedure to determine model coefficients • Weighted height estimate by inverse of height uncertainty 42

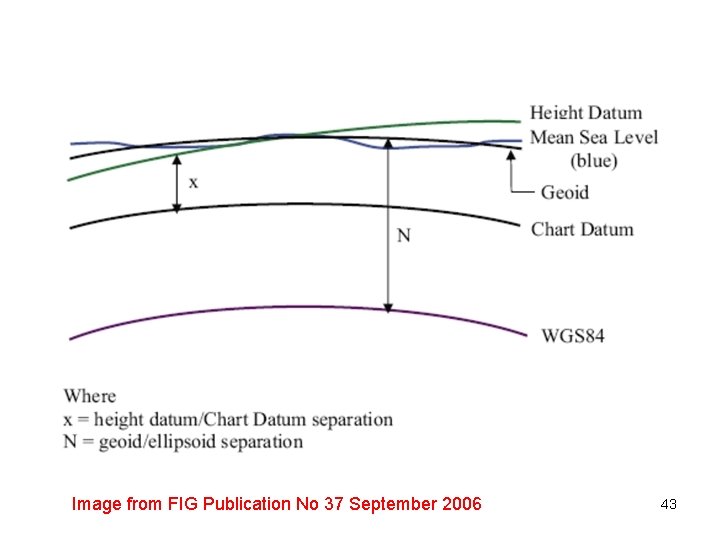
Image from FIG Publication No 37 September 2006 43

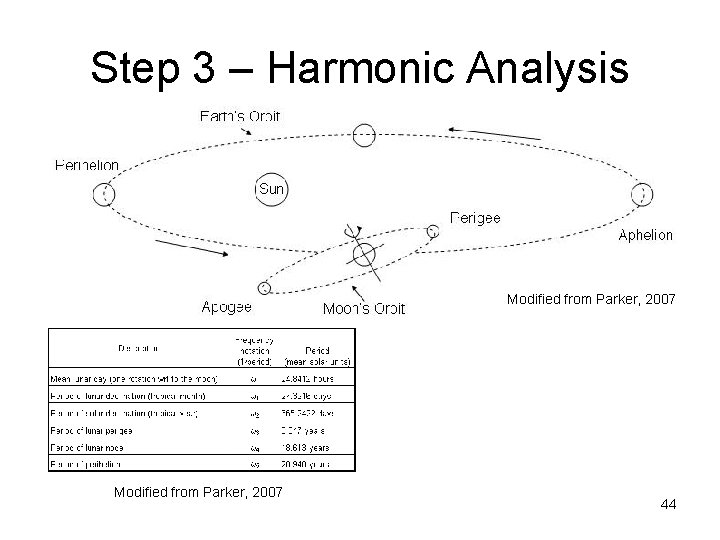
Step 3 – Harmonic Analysis Modified from Parker, 2007 44