ESSnet on Validation A study of VTL Wiesbaden

ESSnet on Validation: A study of VTL Wiesbaden, November 10 -11 2015

Contents – – A study of VTL: rough outline of scope Correctness of VTL – examples Completeness of VTL – examples Some general conclusions 2

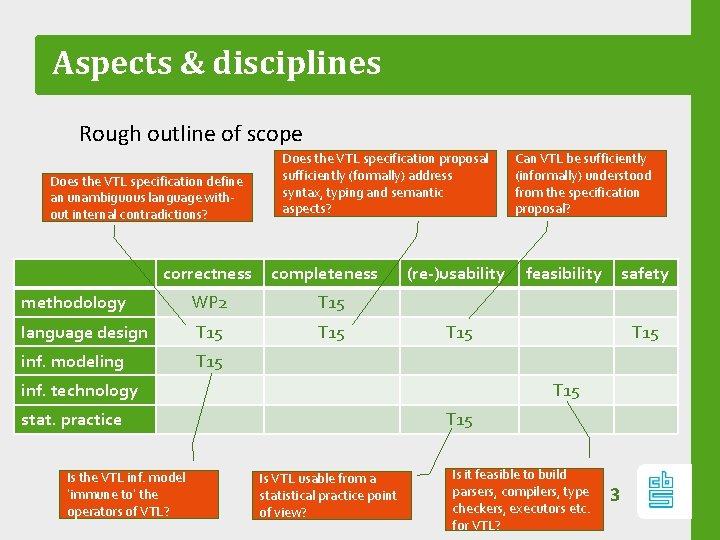
Aspects & disciplines Rough outline of scope Does the VTL specification define an unambiguous language without internal contradictions? correctness Does the VTL specification proposal sufficiently (formally) address syntax, typing and semantic aspects? completeness methodology WP 2 T 15 language design T 15 inf. modeling T 15 (re-)usability feasibility safety T 15 inf. technology T 15 stat. practice Is the VTL inf. model ‘immune to’ the operators of VTL? Can VTL be sufficiently (informally) understood from the specification proposal? T 15 Is VTL usable from a statistical practice point of view? Is it feasible to build parsers, compilers, type checkers, executors etc. for VTL? 3

Correctness: VTL’s operations act on both data sets and data structures. The ideal situation is: The reality however is that some output data sets are not specified by their output data structures (cf. GSIM).

Correctness: VTL’s operations in reality An example is given by the `get’ operator with `union’ mode outputs the following: K 1 K 2 K 3 M 1 1 A X 5 2 B Y 7 yields: union with K 1 K 2 K 3 M 1 1 A X 6 2 B Y 7 3 C Z 9 K 1 K 2 K 3 M 1 1 A X 5 2 B Y 7 1 A X 6 3 C Z 9

Semantics of the ‘=’ operator By allowing data sets that are not properly described by their data structure (cf. GSIM) VTL gives unreliable results for the ‘=’ operator. The semantics of ‘dsl=dsr’ is: K 1 K 2 M 1_COND. 1 A 5 1 A true 1 A 7 1 A false 2 B 7 1 A false 1 A true 2 B true = yields:

Semantics of the ‘=’ operator but K 1 K 2 M 1_COND. 1 A true K 1 K 2 M 1 1 A true 1 A 5 1 A true 2 B 7 2 B true K 1 K 2 M 1_COND. 1 A 5 1 A true 1 A 5 2 B 7 1 A true 2 B 7 2 B true = yields: and = yields:

Completeness: outline of study • Input: Handbook on Validation & survey; • Handbook: validation rule is a Boolean-valued function acting on data sets. (This suggests a logic for describing such a function as a validation rule); • Survey: many nontrivial examples of validation rules – mostly expressed in a(n informal) style; • Study: can a selected number (covering a wide range of validation rules) of them be expressed as VTLstatements? • Also: what is the effect of translation?

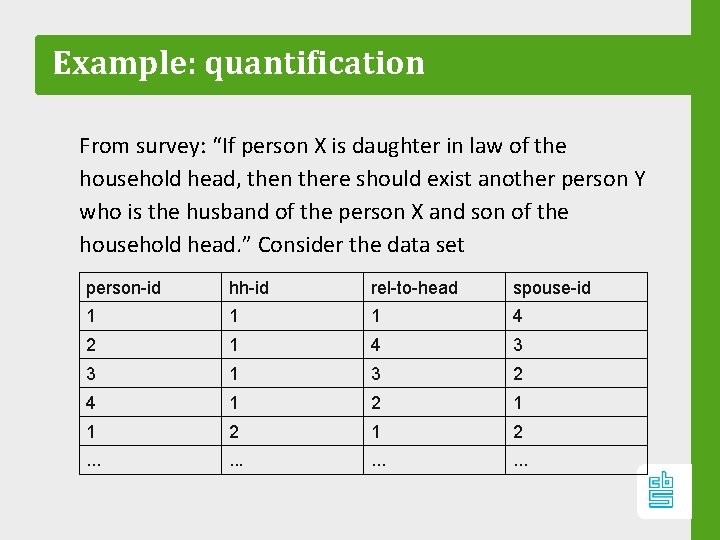
Example: quantification From survey: “If person X is daughter in law of the household head, then there should exist another person Y who is the husband of the person X and son of the household head. ” Consider the data set person-id hh-id rel-to-head spouse-id 1 1 1 4 2 1 4 3 3 1 3 2 4 1 2 1 2 . . .

Example: quantification The validation rule on the previous slide can be expressed compactly using predicate logic (from relational calculus): forall x: IF x. relation_to_head = 4 THEN exists y: x. household-id = y. household-id AND x. spouse-id = y. person-id AND y. relation_to_head = 3

Example: quantification, VTL translation 1)DSfilter : = DS[filter relation_to_head = 4] 2)DSmerge : = merge(DS "DSx", DS "DSy", on (DSy#household_id = DSx#household_id and DSy#spouse_id = DSx#person_id and DSy#relation_to_head = 3 and DSx#relation_to_head = 4), return (DSx#household_id as "household_id", DSx#person_id as "person_id")) 3)DSnot exists : = DSfilter not_exists_in DSmerge 4)DScount : = DSnot exists[calc 1 as "id" role "identifier"][keep (id, person_id)] [aggregate count (person_id)] = 0

A Study of VTL: some conclusions • VTL does not comply with GSIM; • This leads to undesirable results: poor semantics of the equality operator; • Wide range of rules is expressible using VTL; • The translation to VTL of a validation rule is almost never trivial; essence of a rule is lost in translation; • VTL is essentially a SQL-like language for the specification of the steps needed to do validation, instead of the specification of validation rules; • This raises the question of the business case for VTL.