ESSENTIAL STATISTICS 2 E William Navidi and Barry

ESSENTIAL STATISTICS 2 E William Navidi and Barry Monk ©Mc. Graw-Hill Education. All rights reserved. Authorized only for instructor use in the classroom. No reproduction or further distribution permitted without the prior written consent of Mc. Graw-Hill Education.

Tests for Independence and Homogeneity Section 10. 2 ©Mc. Graw-Hill Education.

Objectives 1. Interpret contingency tables 2. Perform tests of independence 3. Perform tests of homogeneity ©Mc. Graw-Hill Education.

Objective 1 Interpret contingency tables ©Mc. Graw-Hill Education.

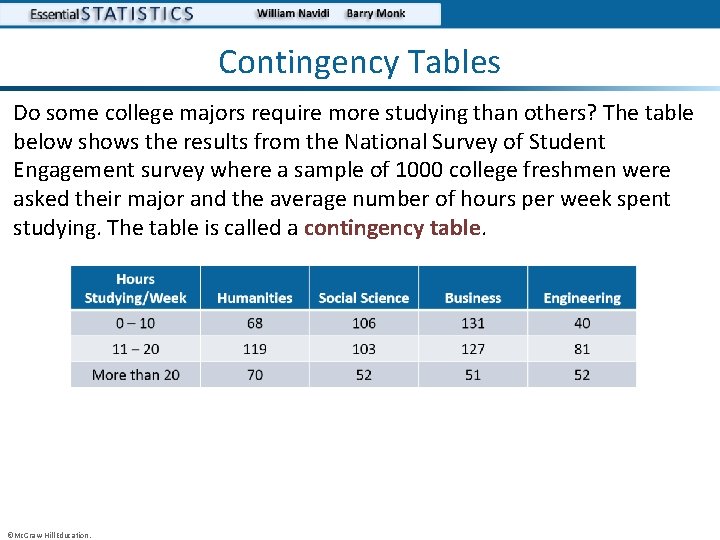
Contingency Tables Do some college majors require more studying than others? The table below shows the results from the National Survey of Student Engagement survey where a sample of 1000 college freshmen were asked their major and the average number of hours per week spent studying. The table is called a contingency table. ©Mc. Graw-Hill Education.

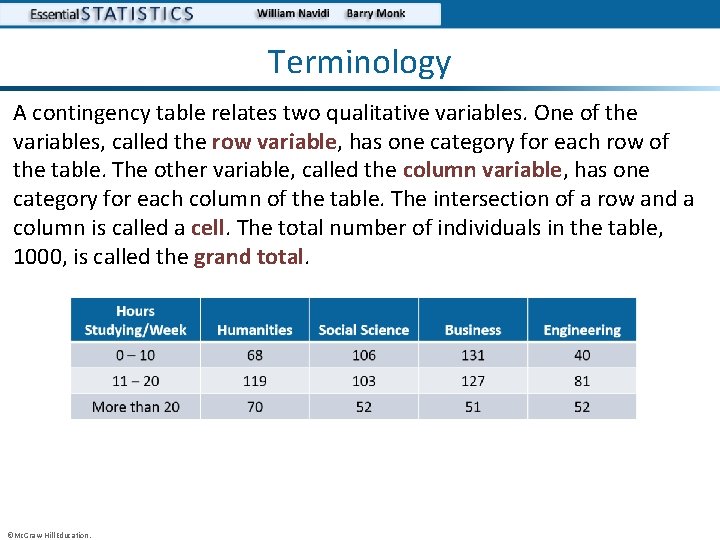
Terminology A contingency table relates two qualitative variables. One of the variables, called the row variable, has one category for each row of the table. The other variable, called the column variable, has one category for each column of the table. The intersection of a row and a column is called a cell. The total number of individuals in the table, 1000, is called the grand total. ©Mc. Graw-Hill Education.

Objective 2 Perform tests of independence ©Mc. Graw-Hill Education.

Dependent versus Independent We are interested in determining whether the distribution of one variable differs, depending on the value of the other variable. If so, the variables are dependent. If the distribution of one variable is the same for all values of the other variable, the variables are independent. In the survey about major and hours spent studying, if these variables are independent, then the distribution of hours studied will be the same for all majors, and the distribution of majors will be the same for all categories of hours studied. ©Mc. Graw-Hill Education.

Test of Independence • ©Mc. Graw-Hill Education.

Example: Expected Frequencies The null hypothesis states that hours studying and major are independent. By using the multiplication rule for independent events, we can compute the expected frequencies. • ©Mc. Graw-Hill Education.

Expected Frequency • ©Mc. Graw-Hill Education.

Performing a Test of Independence • ©Mc. Graw-Hill Education.

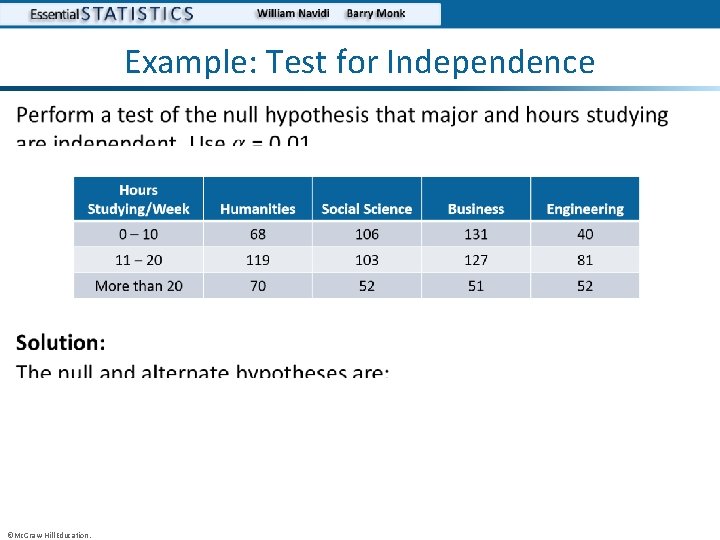
Example: Test for Independence • • ©Mc. Graw-Hill Education.

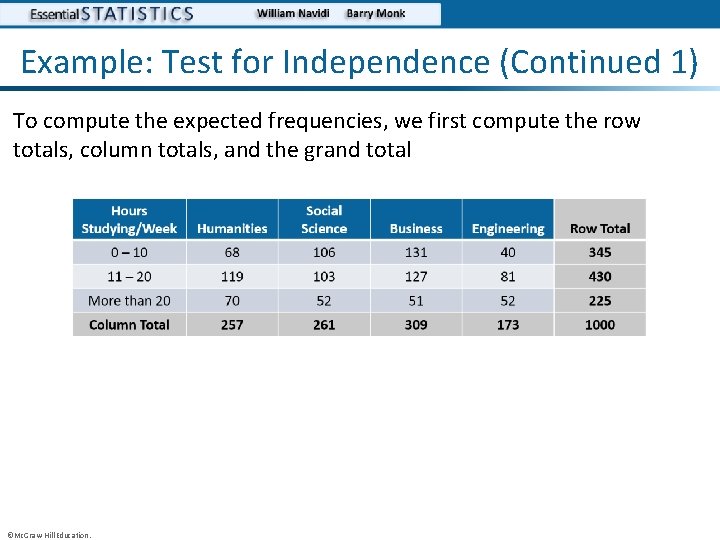
Example: Test for Independence (Continued 1) To compute the expected frequencies, we first compute the row totals, column totals, and the grand total ©Mc. Graw-Hill Education.

Example: Test for Independence (Continued 2) • ©Mc. Graw-Hill Education.

Example: Test for Independence (Continued 3) The expected frequencies are given as follows. All of the expected frequencies are at least 5, so we may proceed. ©Mc. Graw-Hill Education.

Example: Test for Independence (Continued 4) The following table shows the observed and expected frequencies. • ©Mc. Graw-Hill Education.

Example: Test for Independence (Continued 5) There are r = 3 rows and c = 4 columns, so the number of degrees of freedom is (3 − 1)(4 − 1) = 6. From Table A. 4, we find that the critical value corresponding to 6 degrees of freedom and α = 0. 01 is 16. 812. • ©Mc. Graw-Hill Education. •

Hypothesis Testing on the TI-84 PLUS • ©Mc. Graw-Hill Education.

Example: Test for Independence (TI-84 PLUS) • ©Mc. Graw-Hill Education.

Objective 3 Perform tests of homogeneity ©Mc. Graw-Hill Education.

Test of Homogeneity In the contingency table we have seen so far, the individuals in the table were sampled from a single population. For each individual, the values of both the row and column variables were random. In some cases, values of one of the variables (say, the row variable) are assigned by the investigator, and are not random. In these cases, we consider the rows as representing separate populations, and we are interested in testing the hypothesis that the distribution of the column variable is the same for each row. This is known as a test of homogeneity. ©Mc. Graw-Hill Education.

Performing Tests of Homogeneity In a test of homogeneity, we are testing the hypothesis that the distribution of outcomes is the same for each row. The method for performing a test of homogeneity is identical to the method for performing a test of independence. ©Mc. Graw-Hill Education.

Example: Test of Homogeneity Test the hypothesis that the distribution of outcomes is the same for all three treatment groups in the example about the drugs telmisartan and rampiral. Use the α = 0. 05 level. Solution: The null hypothesis says that the distribution of outcomes (fatal heart attack, nonfatal heart attack, no heart attack) is the same for all the drug treatments. The alternate hypothesis says that the distribution of outcomes is not the same for all the treatments. ©Mc. Graw-Hill Education.

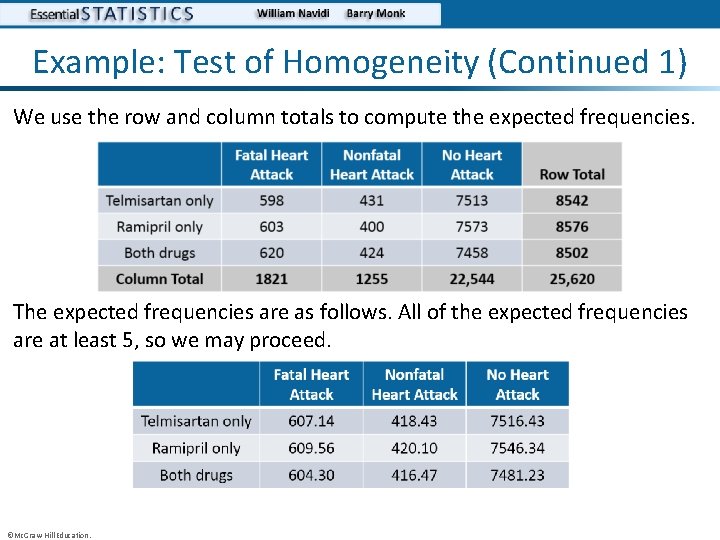
Example: Test of Homogeneity (Continued 1) We use the row and column totals to compute the expected frequencies. The expected frequencies are as follows. All of the expected frequencies are at least 5, so we may proceed. ©Mc. Graw-Hill Education.

Example: Test of Homogeneity (Continued 2) The following table shows the observed and expected frequencies. • • ©Mc. Graw-Hill Education.

You Should Know. . . • How to interpret contingency tables • How to perform tests of independence • How to perform tests of homogeneity ©Mc. Graw-Hill Education.