Essential Question What is a sequence and how












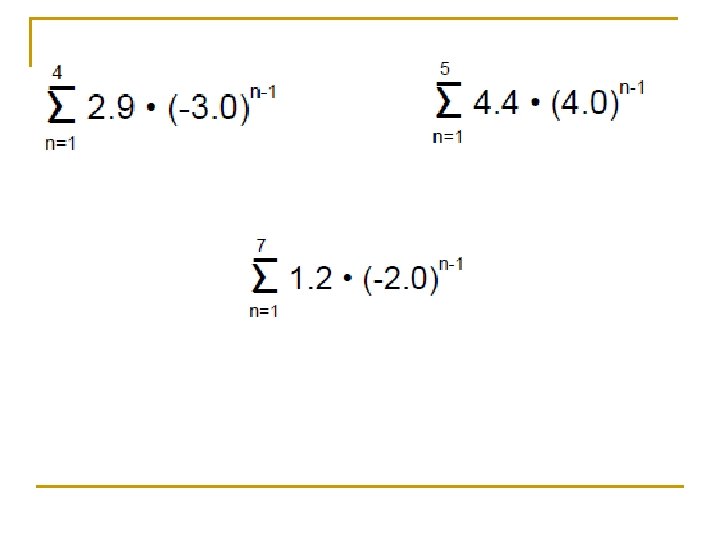











- Slides: 27

Essential Question: What is a sequence and how do I find its terms and sums? How do I find the sum & terms of geometric sequences and series?

Geometric Sequences Geometric Sequence– a sequence whose consecutive terms have a common ratio.

Ex. 1 Are these geometric? 2, 4, 8, 16, …, formula? , … 12, 36, 108, 324, …, Yes 2 n Yes formula? , … 4(3)n No ( -1)n /3 1, 4, 9, 16, …, formula? , … No n 2

Finding the nth term of a Geometric Sequence a n = a 1 rn – 1

Ex. 2 b Write the first five terms of the geometric sequence whose first term is a 1 = 9 and r = (1/3).

Ex. 3 Find the 15 th term of the geometric sequence whose first term is 20 and whose common ratio is 1. 05 a n = a 1 rn – 1 a 15 = (20)(1. 05)15 – 1 a 15 = 39. 599

Ex. 4 Find a formula for the nth term. 5, 15, 45, … a n = a 1 rn – 1 an = 5(3)n – 1 What is the 9 th term? an = 5(3)n – 1 a 9 = 5(3)8 a 9 = 32805

Finite vs. Infinite Geometric Series • What was the difference between an infinite sequence and a finite sequence? • A finite sequence has a specific number of terms whereas an infinite sequence listing terms continually • Finite and infinite series follow the same pattern

sum of a finite geometric series

Ex. 6 Find the sum of the first 12 terms of the series 4(0. 3)n = 4(0. 3)1 + 4(0. 3)2 + 4(0. 3)3 + … + 4(0. 3)12 = 1. 714

Ex. 7 Find the sum of the first 5 terms of the series 5/3 + 5 + 15 + … r = 5/(5/3) = 3 = 605/3

Ex 8. 2. 3 -6+12 -24 … n= 5 3. a 1= -2, r = 3, Sn= -242
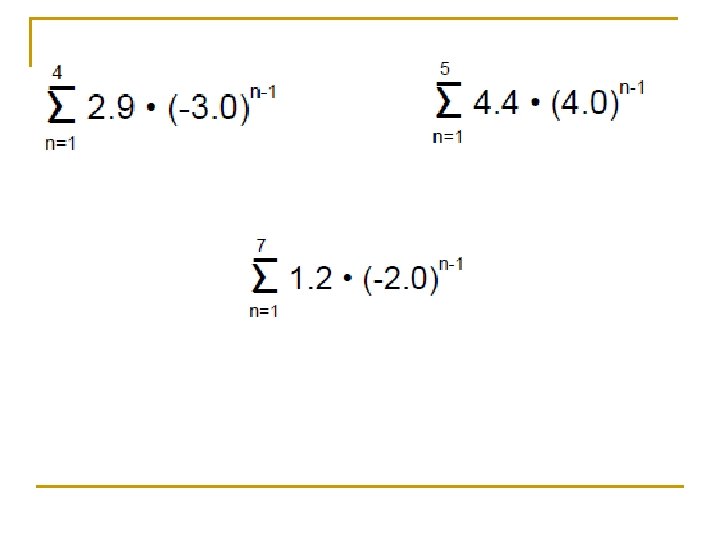

r=3

What would happen if the series was Infinite? Could you find the sum? • Arithmetic Infinite: No Sum • Geometric Infinite: There can be a sum depending on r value. • Geometric – If r > 1, then there is no sum (called Divergent) • Geometric – If r< 1 then there is a sum (called Convergent)

Formula for Infinite Convergent Geometric Series:

1, 4, 7, 10, 13, …. Infinite Arithmetic 3, 7, 11, …, 51 Finite Arithmetic 1, 2, 4, …, 64 Finite Geometric 1, 2, 4, 8, … Infinite Geometric r>1 r < -1 Infinite Geometric -1 < r < 1 No Sum - Diver Convergent

Decide if it is convergent or divergent, then Find the sum, if possib

Decide if it is convergent or divergent, then Find the sum, if possib

Decide if it is convergent or divergent, then Find the sum, if possib

Decide if it is convergent or divergent, then Find the sum, if possib :

1. 3. 2. 125+25+5+1+… 4. Find the common ratio for the infinite geometric series if a 1=81, S=60. 75

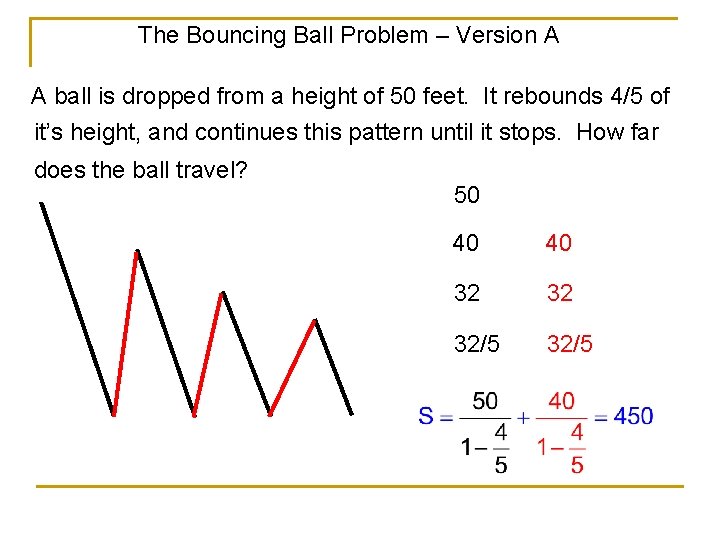
The Bouncing Ball Problem – Version A A ball is dropped from a height of 50 feet. It rebounds 4/5 of it’s height, and continues this pattern until it stops. How far does the ball travel? 50 40 40 32 32 32/5

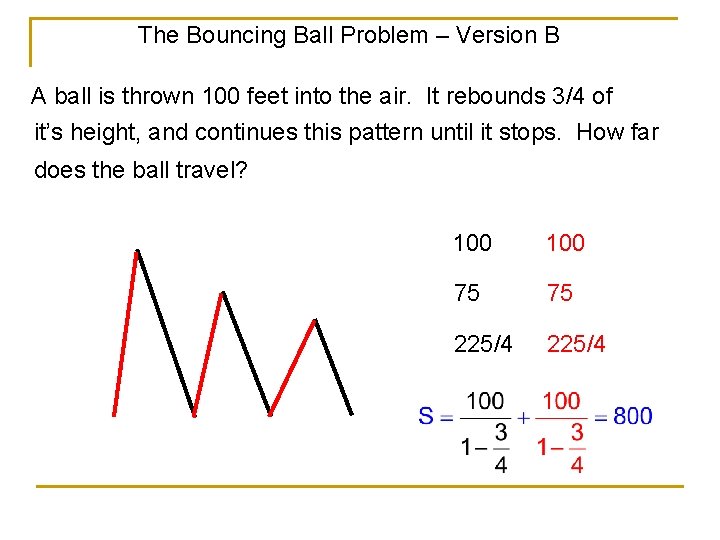
The Bouncing Ball Problem – Version B A ball is thrown 100 feet into the air. It rebounds 3/4 of it’s height, and continues this pattern until it stops. How far does the ball travel? 100 75 75 225/4

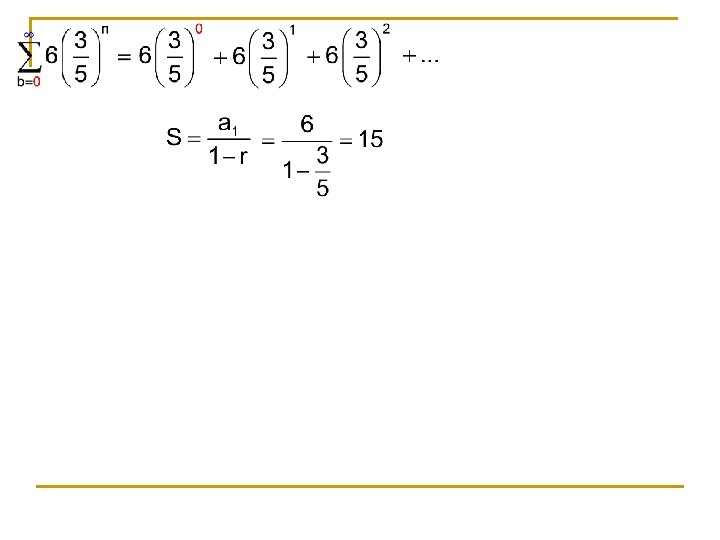
The sum of the first n terms of a sequence is represented by summation notation. upper limit of summation index of summation lower limit of summation

Write out a few terms. If the index began at i = 0, you would have to adjust your formula
