Essential Question What is a sequence and how

Geometric Sequences Geometric Sequence– a sequence whose consecutive terms have a common ratio.

Geometric Sequence A sequence is geometric if the ratios of conse terms are the

Ex. 1 Are these geometric? 2, 4, 8, 16, …, formula? , … 12,

Finding the nth term of a Geometric Sequence a n = a 1 rn

Ex. 2 b Write the first five terms of the geometric sequence whose first

Ex. 3 Find the 15 th term of the geometric sequence whose first term

Ex. 4 Find a formula for the nth term. 5, 15, 45, … a

Ex. 6 Find the sum of the first 12 terms of the series 4(0.

Ex. 7 Find the sum of the first 5 terms of the series 5/3

1, 4, 7, 10, 13, …. Infinite Arithmetic 3, 7, 11, …, 51 Finite

The Bouncing Ball Problem – Version A A ball is dropped from a height

The Bouncing Ball Problem – Version B A ball is thrown 100 feet into

The sum of the first n terms of a sequence is represented by summation

Write out a few terms. If the index began at i = 0, you

Slides: 22

Download presentation

Essential Question: What is a sequence and how do I find its terms and sums? How do I find the sum & terms of geometric sequences and series?

Geometric Sequences Geometric Sequence– a sequence whose consecutive terms have a common ratio.

Geometric Sequence A sequence is geometric if the ratios of conse terms are the same. The number r is the common ratio

Ex. 1 Are these geometric? 2, 4, 8, 16, …, formula? , … 12, 36, 108, 324, …, Yes 2 n Yes formula? , … 4(3)n No ( -1)n /3 1, 4, 9, 16, …, formula? , … No n 2

Finding the nth term of a Geometric Sequence a n = a 1 rn – 1

Ex. 2 b Write the first five terms of the geometric sequence whose first term is a 1 = 9 and r = (1/3).

Ex. 3 Find the 15 th term of the geometric sequence whose first term is 20 and whose common ratio is 1. 05 a n = a 1 rn – 1 a 15 = (20)(1. 05)15 – 1 a 15 = 39. 599

Ex. 4 Find a formula for the nth term. 5, 15, 45, … a n = a 1 rn – 1 an = 5(3)n – 1 What is the 9 th term? an = 5(3)n – 1 a 9 = 5(3)8 a 9 = 32805

sum of a finite geometric series

Ex. 6 Find the sum of the first 12 terms of the series 4(0. 3)n = 4(0. 3)1 + 4(0. 3)2 + 4(0. 3)3 + … + 4(0. 3)12 = 1. 714

Ex. 7 Find the sum of the first 5 terms of the series 5/3 + 5 + 15 + … r = 5/(5/3) = 3 = 605/3

1, 4, 7, 10, 13, …. Infinite Arithmetic 3, 7, 11, …, 51 Finite Arithmetic 1, 2, 4, …, 64 Finite Geometric 1, 2, 4, 8, … Infinite Geometric r>1 r < -1 Infinite Geometric -1 < r < 1 No Sum

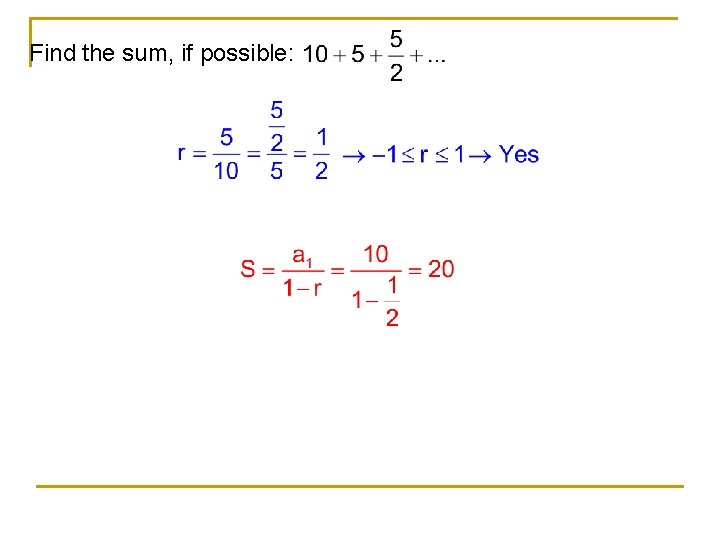
Find the sum, if possible:

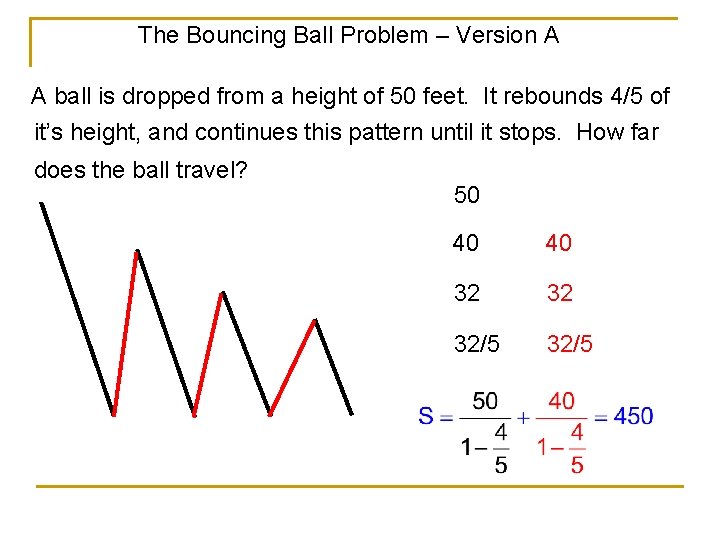
The Bouncing Ball Problem – Version A A ball is dropped from a height of 50 feet. It rebounds 4/5 of it’s height, and continues this pattern until it stops. How far does the ball travel? 50 40 40 32 32 32/5

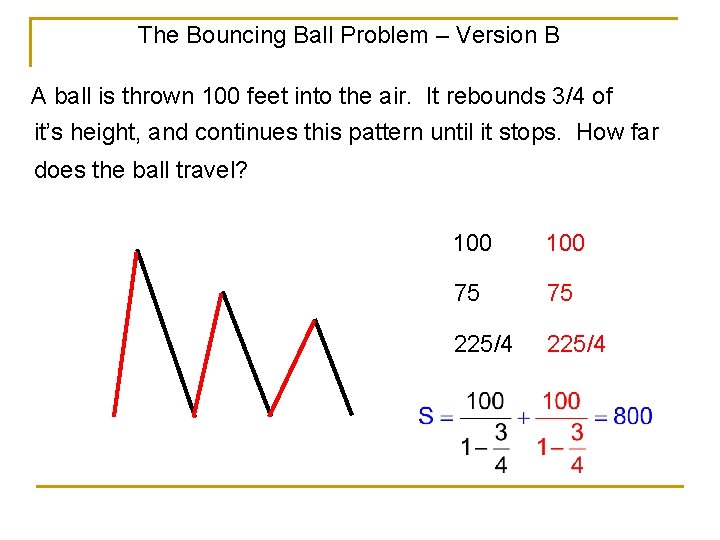
The Bouncing Ball Problem – Version B A ball is thrown 100 feet into the air. It rebounds 3/4 of it’s height, and continues this pattern until it stops. How far does the ball travel? 100 75 75 225/4

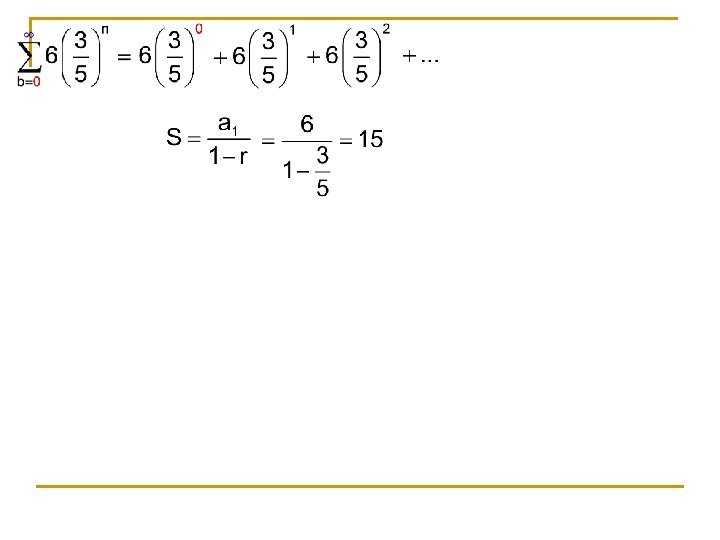
The sum of the first n terms of a sequence is represented by summation notation. upper limit of summation index of summation lower limit of summation

Write out a few terms. If the index began at i = 0, you would have to adjust your formula