Essential Question How can a probability model be

Essential Question How can a probability model be applied to real-world applications?

Warm Up

Bernoulli Trials CHAPTER 16

Special Cases in Probability 3 Conditions: • Only 2 possible outcomes: success or failure • Probability is the same for every trial • Trials are independent (if not, can treat as independent if the sample size<10% of population)

Examples: • Flipping coin • Passing test • Quality control • Free throws in basketball • Flight delayed/on time • Yes/No vote

Examples: • Flipping coin • Passing test • Quality control • Free throws in basketball • Flight delayed/on time • Yes/No vote • Only 2 possible outcomes: success or failure • Probability is the same for every trial • Trials are independent

Example 1 p. 430 #2 Do these situations involve Bernoulli trials? Explain. a) You are rolling 5 dice and need to get at least two 6’s to win the game. b) We record the distribution of eye colors found in a group of 500 people. c) A manufacturer recalls a doll because about 3% have buttons that are not properly attached. Customers return 37 of these dolls to the local toy store. Is the manufacturer likely to find any dangerous buttons?

Example 1 p. 430 #2 d) A city council of 11 Republicans and 8 Democrats picks a committee of 4 at random. What’s the probability they choose all Democrats? e) A 2002 Rutgers University study found that 74% of high school students have cheated on a test at least once. Your local high school principal conducts a survey in homerooms and gets responses that admit to cheating from 322 of the 481 students.

1. Geometric Model – Waiting for Success A new sales gimmick has 30% of the M&M’s covered with speckles. These “groovy” candies are mixed randomly with the normal candies as they are put into the bags for distribution and sale. You buy a bag and remove candies one at a time looking for the speckles. How is this a Bernoulli Trial? What’s the probability that the first speckled one we see is the fourth candy we get?

1. Geometric Model – Waiting for Success What’s the probability that the first speckled one is the tenth one? Write a general formula. What’s the probability the first speckled one is one of the first three we look at?

1. Geometric Model – Waiting for Success p – probability of success q – probability of failure x – number of trials till first success

Example 1 Only about 6% of people have O-negative blood. 1. If donors line up at random for a blood drive, how many do you expect to examine before you find someone who has O-negative blood? 2. What’s the standard deviation? 3. What’s the probability that the first O-negative donor found is the fifth person in line?

Example 2 Suppose a computer chip manufacturer rejects 2% of the chips produced because they fail presale testing. a) What’s the probability that the fourth chip you test is the first bad one you find? b) How many do you expect to test before finding a bad one? c) What is the standard deviation?

Example 3 Carla makes random guesses on her Statistics multiple-choice test, which has five choices for each question. a. How many questions Carla answers until she gets one correct? b. What is the probability that Carla’s first correct answer occurs on Question 9? c. What is the probability that Carla’s first correct answer occurs on Question 7?

Example 4 According to a 2000 study by the Bureau of Justice Statistics, approximately 2% of the nation’s 72 million children had a parent behind bars – nearly 1. 5 million minors. Find the probability that we do not find a child with an incarcerated parent within the first two children we interview.

Example 5 In a test for ESP (extrasensory perception), a subject is told that cards the experimenter can see but the subject cannot contain a star, a circle, a wave, or a square. As the experimenter looks at each card in turn, the subject names the shape on the card. A subject who is just guessing has probability 0. 25 of guessing correctly on each card. a. What is the probability of the subject obtaining his/her first correct guess on the 4 th question? B. What is the probability of the subject obtaining his/her first correct guess within the first 4 questions?

2. Binomial Model – Counting Successes What’s the probability that we’ll find two speckled ones in a handful of five candies?

2. Binomial Model – Counting Successes What’s the probability that we’ll find two speckled ones in a handful of five candies? x – number of successes in n trials

2. Binomial Model – Counting Successes What’s the probability that we’ll find two speckled ones in a handful of five candies? x – number of successes in n trials p – probability of success q – probability of failure

2. Binomial Model – Counting Successes p – probability of success q – probability of failure x – number of successes in n trials

Example 1 Suppose a computer chip manufacturer rejects 2% of the chips produced because they fail presale testing. a) What’s the probability you find a bad one within the first 10 you examine? b) In a random sample of 400 chips, what is the mean number of chips that are expected to fail. c) What is the standard deviation of the sample?

Example 2 Suppose 20 donors come to a blood drive. Recall that 6% of people are “universal donors. ” 1. What are the mean and standard deviation of the number of universal donors among them? 2. What is the probability that there are 2 or 3 universal donors?

Example 3 Assume that 13% of people are left-handed. If we select 5 people at random, find the probability of each outcome described below. a) The first lefty is the fifth person chosen. b) The first lefty is the second or third person.

Example 3 Assume that 13% of people are left-handed. If we select 5 people at random, find the probability of each outcome described below. c) There are exactly 3 lefties in the group. d) There at least 3 lefties in the group. e) There are no more than 3 lefties in the group.

Example 3 Assume that 13% of people are left-handed. If we select 5 people at random, find the probability of each outcome described below. f) There are some lefties among the 5 people.

Review About 8% of males are colorblind. A researcher needs some colorblind subjects for an experiment and begins checking potential subjects. a) On average, how many men should the researcher expect to check to find one who is colorblind?

Review

Review About 8% of males are colorblind. A researcher needs some colorblind subjects for an experiment and begins checking potential subjects. b) What’s the probability that she find 2 colorblind among the first 20 men she checks?

Review

Review About 8% of males are colorblind. A researcher needs some colorblind subjects for an experiment and begins checking potential subjects. c) What’s the probability that the first colorblind man found will be the sixth person checked?

Review

Review Which of the following is a valid probability distribution? (A) (B) X 1 2 3 4 P(X) 0. 3 0. 2 0. 1 X 1 2 3 4 P(X) 0. 2 0. 6 0. 2 0. 1 X -2 -1 1 2 0. 5 -0. 3 0. 5 -2 -1 1 2 0. 3 0. 5 0. 1 (C) P(X) X (D) P(X)

Review

Review Which of the following random variables has geometric model? (A) The number of cards of each suit in a 10 -card hand (B) The number of teachers among a group of randomly chosen adults (C) The number of people we check until we find someone with green eyes (D)The number of Tiger Woods’ pictures in 1200 cereal boxes (E) The number of aces among the top 10 cards in a well-shuffled deck

Warm Up Among employed women, 25% have never been married. Select 10 employed women at random. What is the probability that 5 of the women in the sample have never been married?

Warm Up Among employed women, 25% have never been married. Select 10 employed women at random. What is the probability that 5 of the women in the sample have never been married? 0. 0584

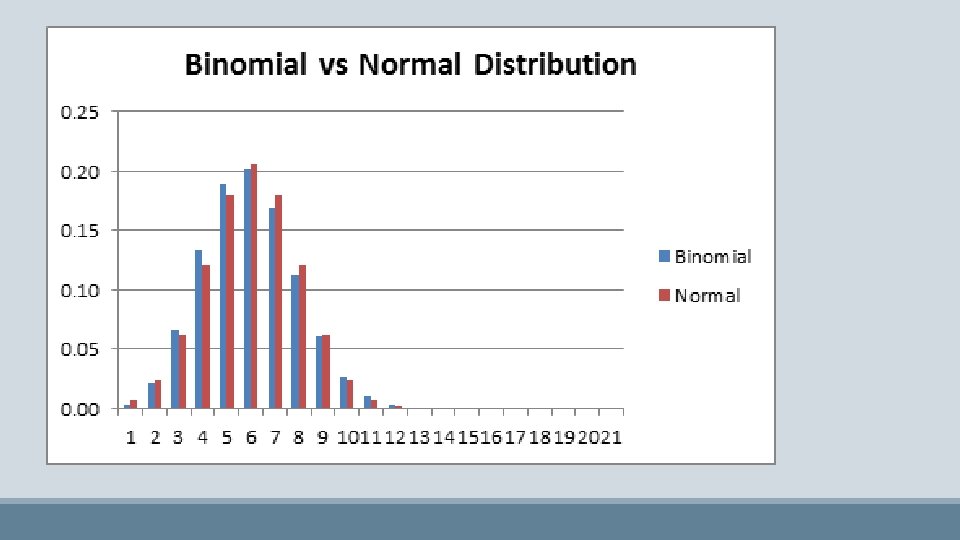
Normal Approximation (how to deal with large n’s) CHAPTER 16

Tennessee Red Cross will collect blood from 32, 000 donors. It anticipates the need of 1850 units of O-negative blood. 6% of people have O-negative blood. How great is the risk that they will fall short? P(X=1850)=

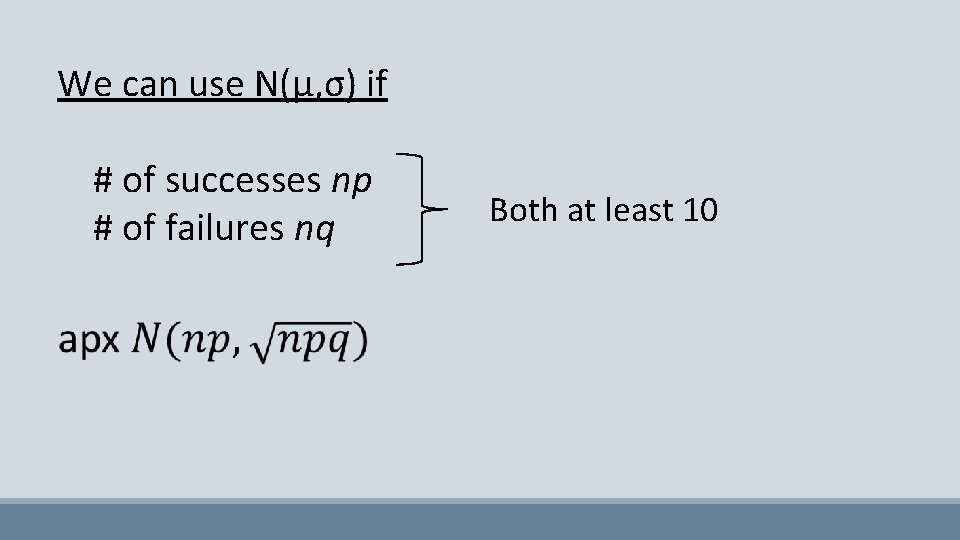
We can use N(µ, σ) if # of successes np # of failures nq Both at least 10

Example 1 An Olympic archer is able to hit the bull’s-eye 80% of the time. Assume each shot is independent of the others. She will be shooting 200 arrows in a large competition. a) What are the mean and standard deviation of the number of bull’s-eyes she might get?

Example 1 An Olympic archer is able to hit the bull’s-eye 80% of the time. Assume each shot is independent of the others. She will be shooting 200 arrows in a large competition. b) Is a Normal model appropriate here? Explain.

Example 1 c) Use the 68– 95– 99. 7 Rule to describe the distribution of the number of bull’s-eyes she may get. d) Would you be surprised if she made only 140 bull’s- eyes? Explain.

Example 2 Pew Research Center (www. pewresearch. org) reports that they are actually able to contact only 76% of the randomly selected households drawn for a telephone survey. Suppose Pew has compiled a list of 1300 phone numbers to call. Find the approximate probability Pew is able to contact at least 1000 voters on their list.

Example 3 An airline, believing that 5% of passengers fail to show up for flights, overbooks (sells more tickets than there are seats). Suppose a plane will hold 265 passengers, and the airline sells 275 tickets. What’s the probability the airline will not have enough seats, so someone gets bumped?

Review

Review Which of the following is a valid probability distribution? (A) (B) (C) X 1 2 3 4 P(X) 0. 3 0. 2 0. 1 X 1 2 3 4 P(X) 0. 2 0. 6 0. 2 0. 1 X -2 -1 1 2 P(X) 0. 5 -0. 3 0. 5 X -2 -1 1 2 0. 3 0. 5 0. 1 (D) P(X)

Review You roll a die. If it comes up a 6, you win $100. If not, you get to roll again. If you get a 6 the second time, you win $50. If not, you lose. a) Create a probability model for the amount you win. b) Find the expected amount you’ll win. c) What would you be willing to pay to play this game?

Review Given the information below, which of the statements is true? X 2 4 6 8 10 P(X) 0. 3 0. 2 0 0. 4 0. 1 A. The variance of the random variable is 1. B. The expected value of the random variable is 11. 6. C. The variance of the random variable is 8. 64. D. The expected value of the random variable is 6. E. The expected value of the random variable is 0.

Review A baseball recruiter visits a high school where a player has a batting average of 0. 450. (This mean he gets a hit in 45% of his at-bats. ) What is the probability that the recruiter must wait for the third atbat in order to see this player get a hit?

Review A baseball recruiter visits a high school where a player has a batting average of 0. 450. (This mean he gets a hit in 45% of his at-bats. ) What is the probability that the player will make exactly 2 out of 3 hits?

Review A delivery company’s trucks occasionally get parking tickets, and based on past experience, the company plans that the trucks will average 1. 3 tickets a month, with a standard deviation of 0. 7 tickets. a) If they have 18 trucks, what are the mean and standard deviation of the total number of parking tickets the company will have to pay this month? b) What assumption did you make in answering?

Extra

Comic Strips Creatively illustrate / discuss / present Options: the topic • Use a blank one • Sketch your own • Write a short play/story Topics: • Combining Random Variables • Binomial Distributions • Geometric Distributions • Binomial vs Geometric Distributions

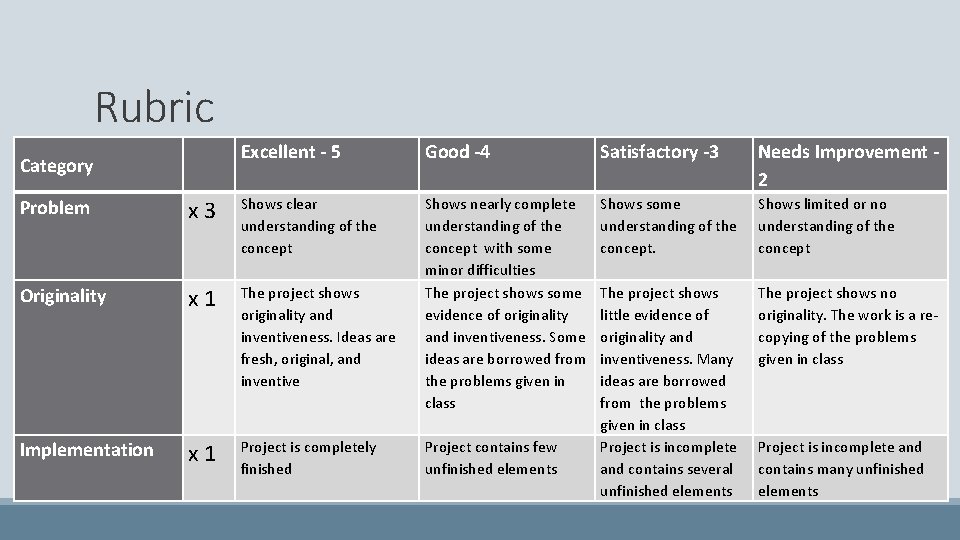
Rubric Category Excellent - 5 Good -4 Satisfactory -3 Needs Improvement - 2 Shows nearly complete understanding of the concept with some minor difficulties The project shows some evidence of originality and inventiveness. Some ideas are borrowed from the problems given in class Shows some understanding of the concept. The project shows little evidence of originality and inventiveness. Many ideas are borrowed from the problems given in class Project is incomplete and contains several unfinished elements Shows limited or no understanding of the concept Problem x 3 Shows clear understanding of the concept Originality x 1 The project shows originality and inventiveness. Ideas are fresh, original, and inventive Implementation x 1 Project is completely finished Project contains few unfinished elements The project shows no originality. The work is a recopying of the problems given in class Project is incomplete and contains many unfinished elements

1. Put your study Guide on the desk in front 2. Cell Phone – in your bag, bag against the wall 3. On your desk: • Index card • Calculator • Pen (pencil) When you are done: 1. Staple together: Your index card Your test Your Study Guide 2. Wait for everyone else to finish