ESS 250 MARS Dave Paige Francis Nimmo ESS

ESS 250: MARS Dave Paige / Francis Nimmo ESS 250 Winter 2003

Lecture Outline • Bulk structure and composition – Geochemical constraints – Geophysical constraints • Properties of the crust and lithosphere – Density, thickness, rigidity – Magnetic properties • Evolution of Mars through time ESS 250 Winter 2003

Bulk Structure and Composition • • • Cosmochemical arguments SNC meteorites Remote sensing In situ measurements Mass and Moment of inertia (Seismology) ESS 250 Winter 2003

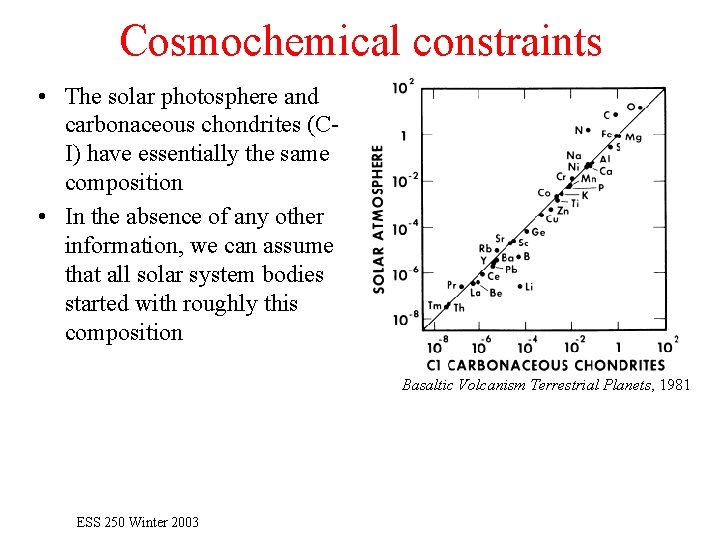
Cosmochemical constraints • The solar photosphere and carbonaceous chondrites (CI) have essentially the same composition • In the absence of any other information, we can assume that all solar system bodies started with roughly this composition Basaltic Volcanism Terrestrial Planets, 1981 ESS 250 Winter 2003

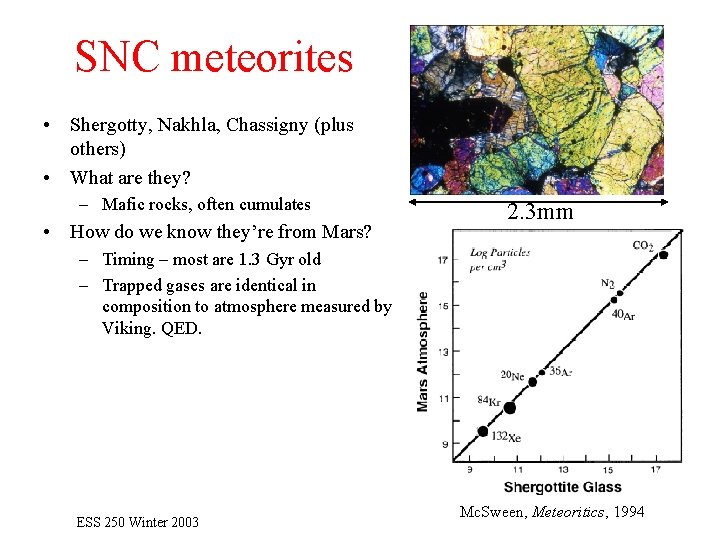
SNC meteorites • Shergotty, Nakhla, Chassigny (plus others) • What are they? – Mafic rocks, often cumulates • How do we know they’re from Mars? 2. 3 mm – Timing – most are 1. 3 Gyr old – Trapped gases are identical in composition to atmosphere measured by Viking. QED. ESS 250 Winter 2003 Mc. Sween, Meteoritics, 1994

What do the SNC’s tell us? • Assume the abundances of a few key elements e. g. Mg, Si, Al (using geophysical, cosmochemical and observational constraints) • Then use ratios to infer abundances of other elements • Without the SNC’s, we would have to simply assume an Earthlike or CI-like mantle Mars Earth Dreibus and Wanke, Meteoritics, 1985 ESS 250 Winter 2003

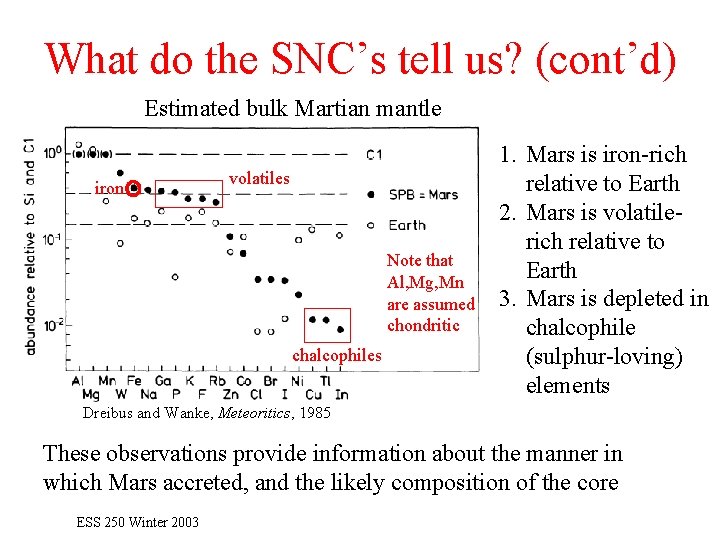
What do the SNC’s tell us? (cont’d) Estimated bulk Martian mantle iron volatiles Note that Al, Mg, Mn are assumed chondritic chalcophiles 1. Mars is iron-rich relative to Earth 2. Mars is volatilerich relative to Earth 3. Mars is depleted in chalcophile (sulphur-loving) elements Dreibus and Wanke, Meteoritics, 1985 These observations provide information about the manner in which Mars accreted, and the likely composition of the core ESS 250 Winter 2003

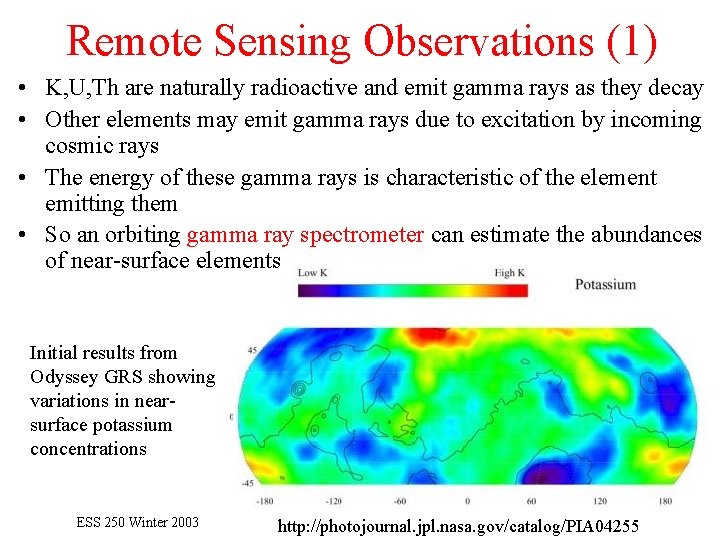
Remote Sensing Observations (1) • K, U, Th are naturally radioactive and emit gamma rays as they decay • Other elements may emit gamma rays due to excitation by incoming cosmic rays • The energy of these gamma rays is characteristic of the element emitting them • So an orbiting gamma ray spectrometer can estimate the abundances of near-surface elements Initial results from Odyssey GRS showing variations in nearsurface potassium concentrations ESS 250 Winter 2003 http: //photojournal. jpl. nasa. gov/catalog/PIA 04255

Remote Sensing (2) • Different minerals have different thermal infrared spectra, controlled mainly by the characteristic bond energies • These energies can be measured remotely by an infra-red spectrometer, and the surface mineralogy determined • Doing so is very tricky, mainly because the effects of the CO 2 atmosphere and atmospheric dust have to be subtracted • There is some ground-truth from Earth which suggests that the technique can work • It has been proposed that there are two types of mineralogy present: a “basaltic” type and an “andesitic” type. The latter is significant because andesites on Earth are associated with subduction zones. • One problem with the data is that IR emissions come from the top few microns, so it is not clear what the subsurface is doing ESS 250 Winter 2003 “basalt” “andesite” Bandfield et al, Science 2000 Using MGS-TES data

In Situ Measurements APXS Mars Pathfinder, 1997 • Pathfinder measured rock and soil compositions using an Alpha Proton X-Ray Spectrometer (APXS) • This works by irradiating a sample with Alpha particles and detecting the particles/radiation given off • The instrument appears not to have been properly calibrated (!), so the results have been subject to revision • The two Viking landers (1976) employed similar technology but only on soil samples (not rocks). ESS 250 Winter 2003

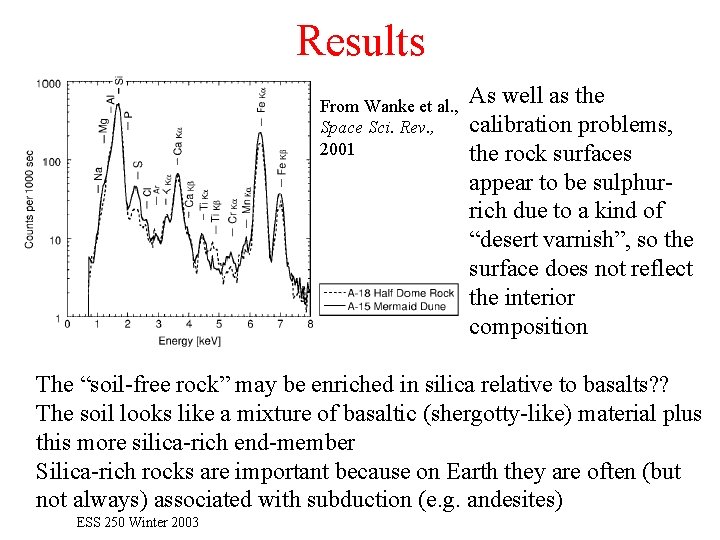
Results From Wanke et al. , Space Sci. Rev. , 2001 As well as the calibration problems, the rock surfaces appear to be sulphurrich due to a kind of “desert varnish”, so the surface does not reflect the interior composition The “soil-free rock” may be enriched in silica relative to basalts? ? The soil looks like a mixture of basaltic (shergotty-like) material plus this more silica-rich end-member Silica-rich rocks are important because on Earth they are often (but not always) associated with subduction (e. g. andesites) ESS 250 Winter 2003

Moment of Inertia • I = S m r 2 • r is perpendicular distance from axis • I of sphere = 0. 4 MR 2 • Objects with mass concentrated in centre have I/MR 2 < 0. 4 • So I tells us about internal structure • Normally, we measure C, the maximum Mo. I m r C = max. moment of inertia A = min. moment of inertia I = (A + B + C)/3 How do we measure it? ESS 250 Winter 2003

Obtaining the Mo. I How do we get moment of inertia (C)? Three steps: 1) Obtain (C-A) from observations of orbiting spacecraft 2) Obtain (C-A)/C from observations of planetary precession 3) Use 1) and 2) to obtain C 1) Gravitational potential of a planet is given by r where R f So observations of the spacecraft orbit* give us J 2 ESS 250 Winter 2003 *The rate at which the node precesses

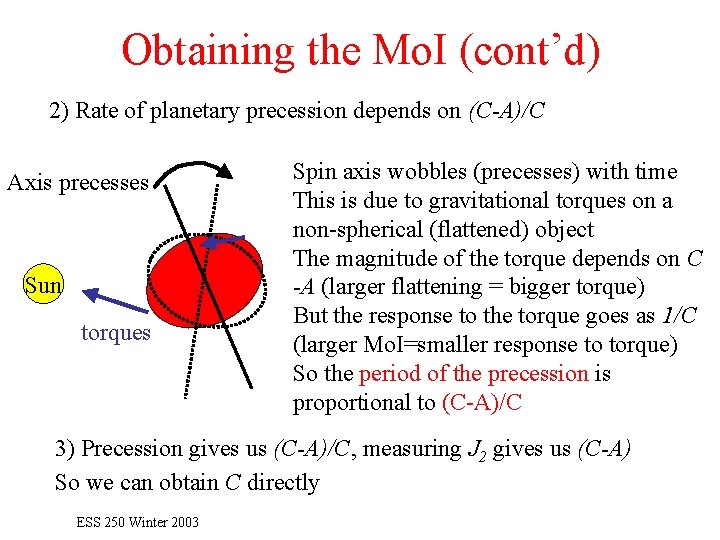
Obtaining the Mo. I (cont’d) 2) Rate of planetary precession depends on (C-A)/C Axis precesses Sun torques Spin axis wobbles (precesses) with time This is due to gravitational torques on a non-spherical (flattened) object The magnitude of the torque depends on C -A (larger flattening = bigger torque) But the response to the torque goes as 1/C (larger Mo. I=smaller response to torque) So the period of the precession is proportional to (C-A)/C 3) Precession gives us (C-A)/C, measuring J 2 gives us (C-A) So we can obtain C directly ESS 250 Winter 2003

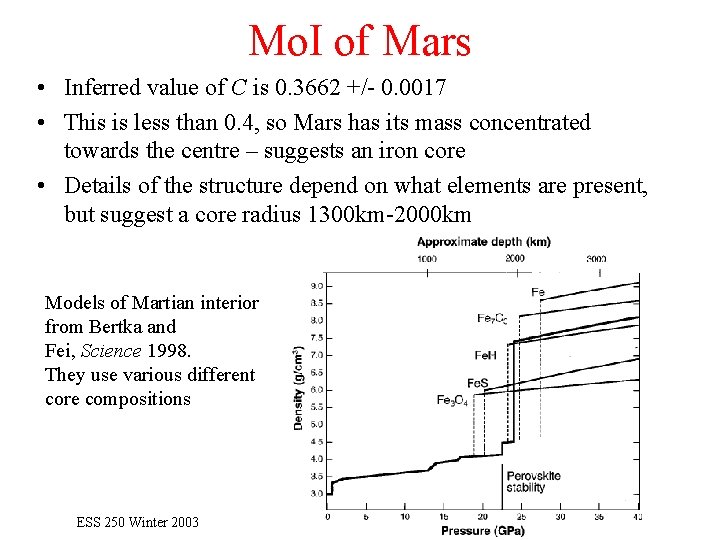
Mo. I of Mars • Inferred value of C is 0. 3662 +/- 0. 0017 • This is less than 0. 4, so Mars has its mass concentrated towards the centre – suggests an iron core • Details of the structure depend on what elements are present, but suggest a core radius 1300 km-2000 km Models of Martian interior from Bertka and Fei, Science 1998. They use various different core compositions ESS 250 Winter 2003

A liquid core (? ) • Just like the Earth, Mars experiences solid-body tides due to the gravitational attraction of the Sun • The response to these tides depends on the interior structure of the planet • In particular, a planet with a (partially) liquid core will deform more than a planet with a solid, rigid core • Because the shape of the planet affects its gravitational potential, the tidal deformation of the planet can be measured by observing the changes in spacecraft orbit • The dimensionless response of the gravity field to the tides is given by the tidal Love number k 2. Liquid core ESS 250 Winter 2003 (large k ) 2 Sun Solid core (small k 2)

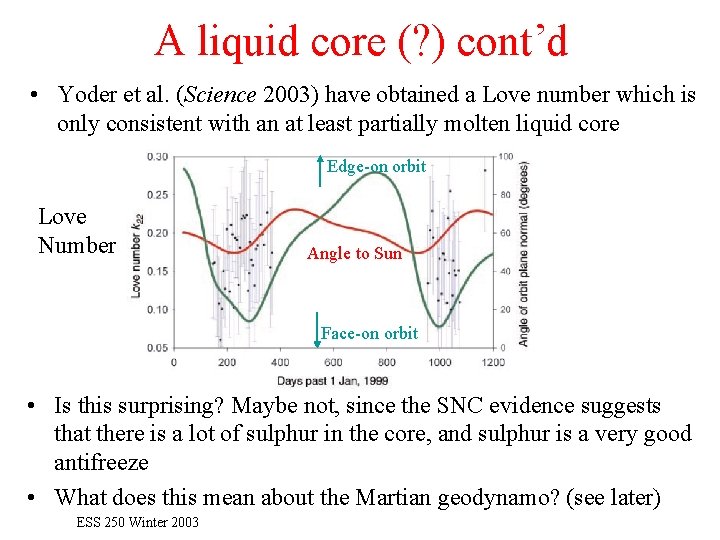
A liquid core (? ) cont’d • Yoder et al. (Science 2003) have obtained a Love number which is only consistent with an at least partially molten liquid core Edge-on orbit Love Number Angle to Sun Face-on orbit • Is this surprising? Maybe not, since the SNC evidence suggests that there is a lot of sulphur in the core, and sulphur is a very good antifreeze • What does this mean about the Martian geodynamo? (see later) ESS 250 Winter 2003

Gravity • Variations in surface gravity cause spacecraft orbit to vary • Orbit variations cause doppler shift in radio signals to Earth • Doppler shift can be used to infer lineof-sight (LOS) velocity changes • With enough observations, the LOS velocity changes can be used to reconstruct the gravity field Line-of-sight (LOS) to Earth z spacecraft surface The importance of gravity measurements is that they provide one of the few ways of inferring the subsurface properties of Mars. Seismology is another (better) way, but it is not a priority for current NASA Mars exploration ESS 250 Winter 2003

Gravity (cont’d) • Requires enormous precision (detect mm/s variations in velocity, orbital velocity is km/s) • Main limitation is spacecraft altitude (determined by atmosphere, ~200 km for Mars) • Gravity signals are attenuated by a factor of exp (- k z) • where k is the wavenumber (=2 p/l) and z is the spacecraft altitude • So it is hard to detect gravity signals with wavelengths shorter than the spacecraft altitude • Same goes for magnetic signals ESS 250 Winter 2003

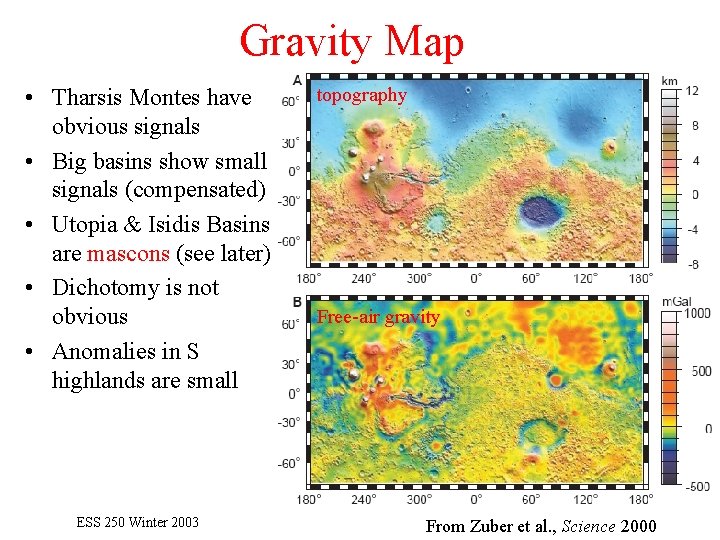
Gravity Map • Tharsis Montes have obvious signals • Big basins show small signals (compensated) • Utopia & Isidis Basins are mascons (see later) • Dichotomy is not obvious • Anomalies in S highlands are small ESS 250 Winter 2003 topography Free-air gravity From Zuber et al. , Science 2000

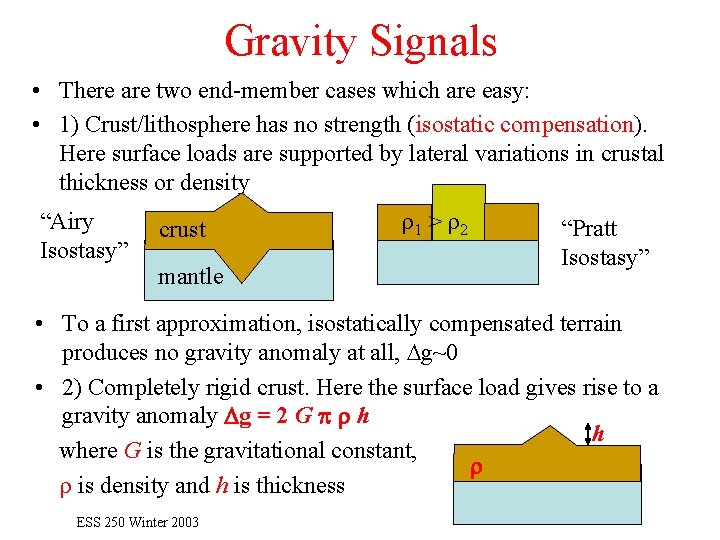
Gravity Signals • There are two end-member cases which are easy: • 1) Crust/lithosphere has no strength (isostatic compensation). Here surface loads are supported by lateral variations in crustal thickness or density “Airy Isostasy” crust mantle r 1 > r 2 “Pratt Isostasy” • To a first approximation, isostatically compensated terrain produces no gravity anomaly at all, Dg~0 • 2) Completely rigid crust. Here the surface load gives rise to a gravity anomaly Dg = 2 G p r h h where G is the gravitational constant, r r is density and h is thickness ESS 250 Winter 2003

Gravity Signals (cont’d) • A rigid load of thickness 1 km and density contrast 1000 kg/m 3 produces a gravity anomaly of 42 m. Gal • 1 m. Gal = 10 -5 m s-2. MGS gravity accuracy is a few m. Gal. • So large gravity anomalies (100’s m. Gal) imply rigidly supported loads, small gravity anomalies imply isostatically supported loads • So we can use gravity to infer how loads are supported on other planets • In order to understand this use of gravity, we need to understand how loads are supported by the lithosphere. . . load ESS 250 Winter 2003 lithosphere

How are loads supported? • A very useful model for how loads are supported assumes that the lithosphere is elastic • Elastic materials deform according to the following equation: (A) • Here D is the rigidity, w is the deflection, r is the density contrast between mantle and surface and L is the load • The rigidity can be expressed as an effective elastic thickness Te • Here E is Young’s modulus and s is Poisson’s ratio • Te is measured in km and is a more intuitive measure than D ESS 250 Winter 2003

How are loads supported? (2) If you assume a sinusoidal load, then you can use equation (A) to infer whether a load is closer to isostatic or rigid support. If the rigidity is very low or the load wavelength is long, you get (Airy) isostatic support; if the rigidity is very large or the load wavelength short, you get rigid support. The crossover from rigidly-supported to isostatically-supported depends on the quantity where D is the rigidity (see above), k is the load wavenumber, Dr is the density contrast between mantle and crust and g is acceleration due to gravity. How do we derive this? This quantity gives the deflection due to a load, relative to the isostatic deflection (it is small for large D, =1 if D=0). ESS 250 Winter 2003

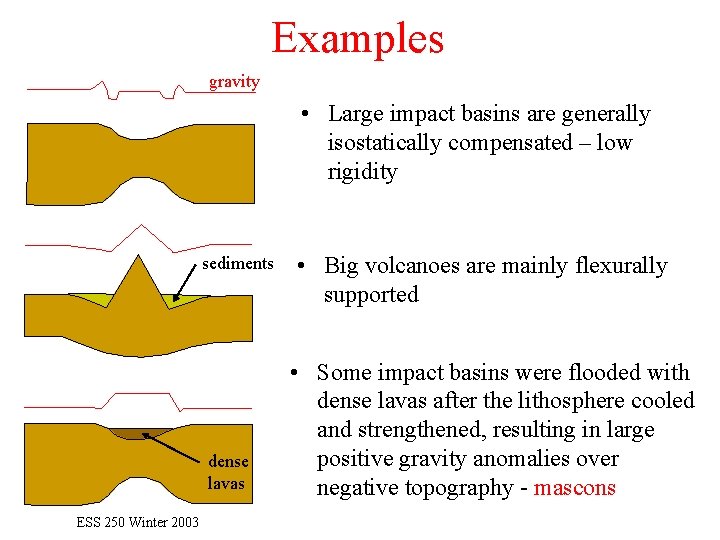
Examples gravity • Large impact basins are generally isostatically compensated – low rigidity sediments dense lavas ESS 250 Winter 2003 • Big volcanoes are mainly flexurally supported • Some impact basins were flooded with dense lavas after the lithosphere cooled and strengthened, resulting in large positive gravity anomalies over negative topography - mascons

Back to Gravity. . . • Isostatic loads produce small gravity anomalies; rigidly supported loads produce large gravity anomalies • Short wavelength loads are rigidly supported; long wavelength loads are isostatically supported • The crossover wavelength depends on the rigidity of the lithosphere • So the gravity as a function of wavelength contains information on how loads are supported • We form a quantity called the admittance, Z(k), which is the ratio of the gravity to the topography at a particular wavelength: Z(k) = g(k) / h(k) • We can plot the calculated admittance from real data and compare it to theoretical predictions to infer the rigidity, density and thickness of the crust/lithosphere ESS 250 Winter 2003

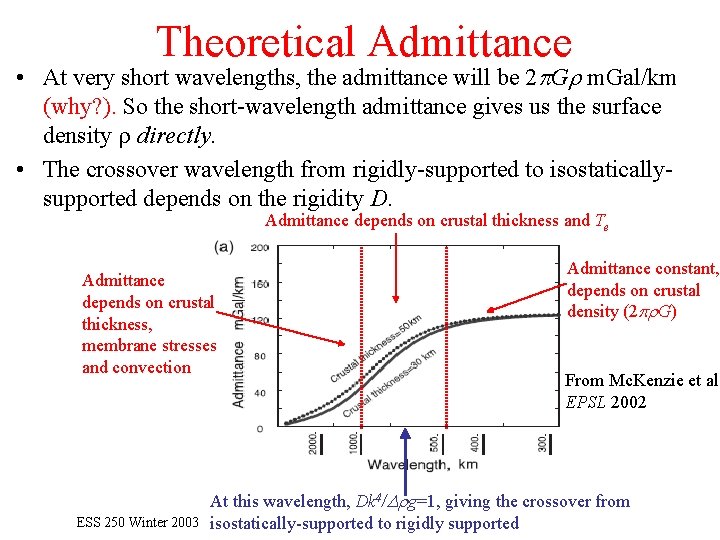
Theoretical Admittance • At very short wavelengths, the admittance will be 2 p. Gr m. Gal/km (why? ). So the short-wavelength admittance gives us the surface density r directly. • The crossover wavelength from rigidly-supported to isostaticallysupported depends on the rigidity D. Admittance depends on crustal thickness and Te Admittance depends on crustal thickness, membrane stresses and convection ESS 250 Winter 2003 Admittance constant, depends on crustal density (2 pr. G) From Mc. Kenzie et al. EPSL 2002 At this wavelength, Dk 4/Drg=1, giving the crossover from isostatically-supported to rigidly supported

Theoretical Admittance (cont’d) • The admittance changes slightly with crustal thickness: a larger crustal thickness gives rise to a slightly higher admittance (why? ) • There are tradeoffs between Te, crustal thickness and r which make it difficult to estimate all three properties (although r can be uniquely determined using short-wavelength data). Why might this not be possible in practice? • If there are subsurface loads, the non-uniqueness problem becomes worse. The presence of subsurface loads gives rise to incoherence between the gravity and topography. • On a small planet such as Mars, the sphericity of the body is important in the elastic deformation equations • Finally, convection can be an important source of topography at long wavelengths (and has a characteristic admittance). ESS 250 Winter 2003

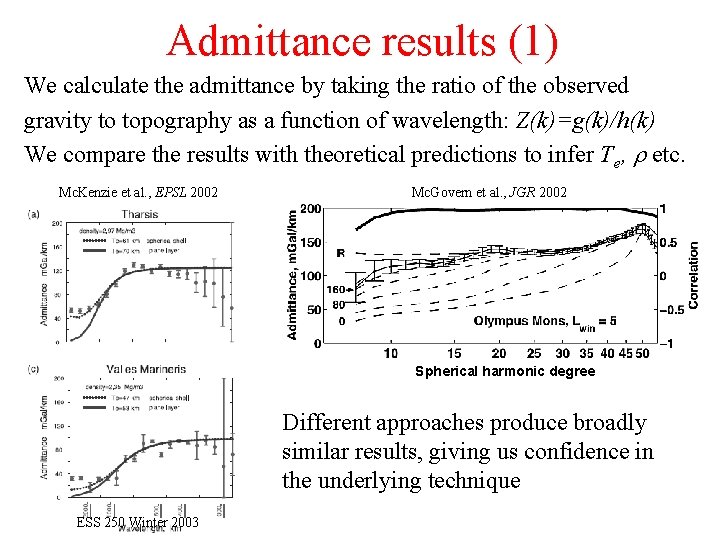
Admittance results (1) We calculate the admittance by taking the ratio of the observed gravity to topography as a function of wavelength: Z(k)=g(k)/h(k) We compare the results with theoretical predictions to infer Te, r etc. Mc. Kenzie et al. , EPSL 2002 Mc. Govern et al. , JGR 2002 Spherical harmonic degree Different approaches produce broadly similar results, giving us confidence in the underlying technique ESS 250 Winter 2003

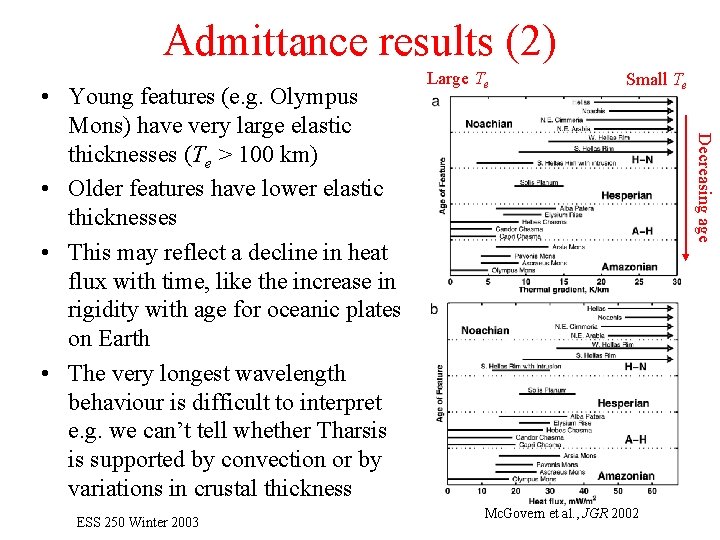
Admittance results (2) ESS 250 Winter 2003 Small Te Decreasing age • Young features (e. g. Olympus Mons) have very large elastic thicknesses (Te > 100 km) • Older features have lower elastic thicknesses • This may reflect a decline in heat flux with time, like the increase in rigidity with age for oceanic plates on Earth • The very longest wavelength behaviour is difficult to interpret e. g. we can’t tell whether Tharsis is supported by convection or by variations in crustal thickness Large Te Mc. Govern et al. , JGR 2002

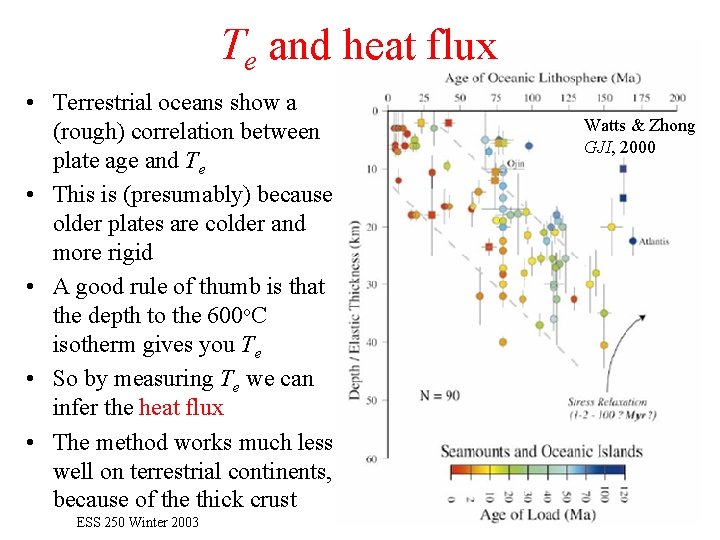
Te and heat flux • Terrestrial oceans show a (rough) correlation between plate age and Te • This is (presumably) because older plates are colder and more rigid • A good rule of thumb is that the depth to the 600 o. C isotherm gives you Te • So by measuring Te we can infer the heat flux • The method works much less well on terrestrial continents, because of the thick crust ESS 250 Winter 2003 Watts & Zhong GJI, 2000

Crustal thickness • We can use the admittance approach to infer the crustal thickness, but there are tradeoffs with Te and density which means the uncertainties are large • An alternative is to assume a mean crustal thickness and use gravity and topography to calculate the crustal thickness variations. This is the approach of Zuber et al. , Science, 2000 and does not require any assumptions about rigidity. • They assume a mean value of 50 km, so that the largest impact basins would not penetrate to the mantle Observed gravity Observed topography Assumed mean crustal thickness ESS 250 Winter 2003 Inferred crustal thickness variation

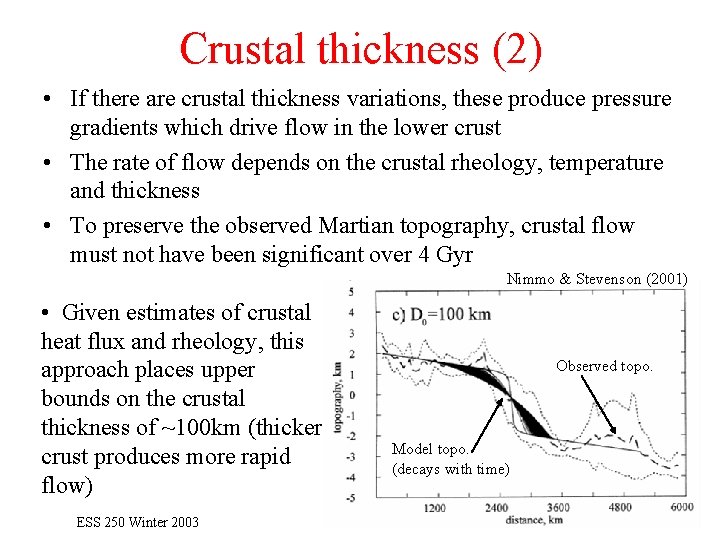
Crustal thickness (2) • If there are crustal thickness variations, these produce pressure gradients which drive flow in the lower crust • The rate of flow depends on the crustal rheology, temperature and thickness • To preserve the observed Martian topography, crustal flow must not have been significant over 4 Gyr Nimmo & Stevenson (2001) • Given estimates of crustal heat flux and rheology, this approach places upper bounds on the crustal thickness of ~100 km (thicker crust produces more rapid flow) ESS 250 Winter 2003 Observed topo. Model topo. (decays with time)

Magnetism • Spatial resolution limited in same way as gravity (e-kz term) • E. g. terrestrial mid-ocean ridge stripe width ~10 km, so they cannot be detected by spacecraft at altitude ~400 km • Magnetic fields are similar to gravity fields, but interpretation is complicated by fact that magnetization is a vector quantity (while mass is a scalar) • Magnetic field (vector) is measured in units of n. T (nano-Tesla) • The Earth’s magnetic field intensity (at the surface) is appx. 40, 000 n. T (varies spatially, slowly varies in time) • Crustal magnetism is due to induced magnetization (from background field) and remanent magnetization (acquired when the rock last cooled below its Curie temperature) • Typical crustal magnetic anomalies are ~100 n. T ESS 250 Winter 2003

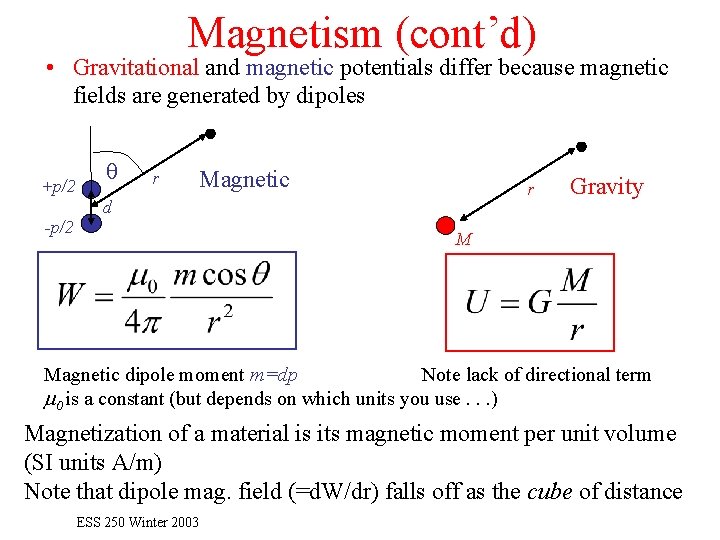
Magnetism (cont’d) • Gravitational and magnetic potentials differ because magnetic fields are generated by dipoles +p/2 -p/2 q r Magnetic r d Gravity M Magnetic dipole moment m=dp Note lack of directional term m 0 is a constant (but depends on which units you use. . . ) Magnetization of a material is its magnetic moment per unit volume (SI units A/m) Note that dipole mag. field (=d. W/dr) falls off as the cube of distance ESS 250 Winter 2003

Magnetic Observations • From the early Mars spacecraft, we know that Mars does not have a global magnetic field like the Earth’s • A big surprise of MGS was that there are large, local magnetic anomalies present From Acuna et al, Science 1999 Note the peculiar projection Largest terrestrial magnetic anomalies are ~100 n. T at similar altitudes ESS 250 Winter 2003

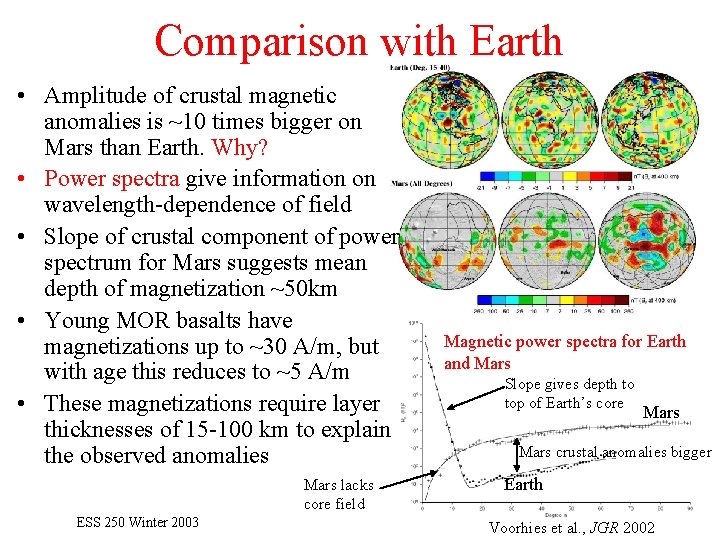
Comparison with Earth • Amplitude of crustal magnetic anomalies is ~10 times bigger on Mars than Earth. Why? • Power spectra give information on wavelength-dependence of field • Slope of crustal component of power spectrum for Mars suggests mean depth of magnetization ~50 km • Young MOR basalts have magnetizations up to ~30 A/m, but with age this reduces to ~5 A/m • These magnetizations require layer thicknesses of 15 -100 km to explain the observed anomalies Mars lacks core field ESS 250 Winter 2003 Magnetic power spectra for Earth and Mars Slope gives depth to top of Earth’s core Mars crustal anomalies bigger Earth Voorhies et al. , JGR 2002

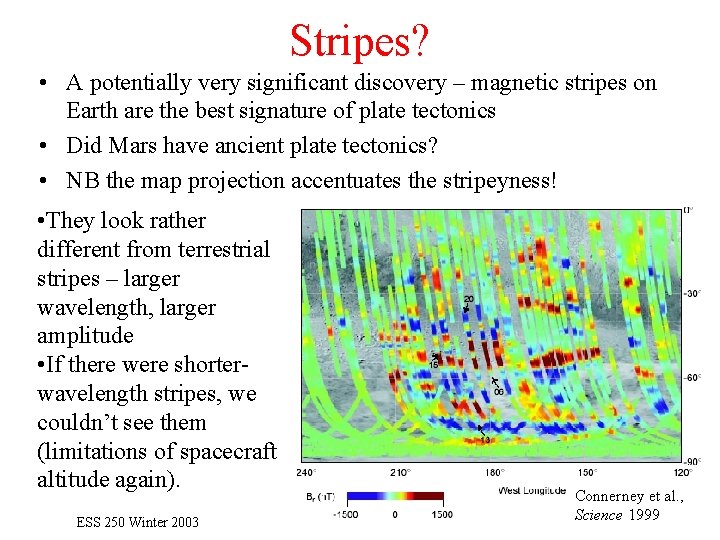
Stripes? • A potentially very significant discovery – magnetic stripes on Earth are the best signature of plate tectonics • Did Mars have ancient plate tectonics? • NB the map projection accentuates the stripeyness! • They look rather different from terrestrial stripes – larger wavelength, larger amplitude • If there were shorterwavelength stripes, we couldn’t see them (limitations of spacecraft altitude again). ESS 250 Winter 2003 Connerney et al. , Science 1999

What use are they? • The fact that the large impact basins do not show any magnetic anomalies suggests that the Martian dynamo was not operating at the time these basins formed (~4 Gyr B. P. ) • The ancient Martian meteorite ALH 84001 does show magnetization, suggesting that the Martian dynamo operated early in Mars’ history, and then stopped (see later) • The depth of the anomalies tells us something about the temperature structure of the crust (parts of the crust that exceed the Curie Temperature will not retain magnetisation) • How do we estimate the depth of the anomaliess? : – Power spectral approaches (see before) ~50 km – Effects of impact craters (big ones show demagnetization, small ones don’t – critical size depends on thickness of magnetized layer) ~50 km – Layer must be thick enough to produce correct amplitude – depends on the magnetization of the material (see before) ~15 -100 km ESS 250 Winter 2003

Evolution of Mars • • • What constraints do we have? Te varies with age – can be linked to changing heat flux Magnetic field operated early on, then stopped Present-day state of core (at least partially molten) Present-day crustal thickness (but how and when it formed is uncertain) • Volcanism – voluminous early on, but has carried on at a reduced rate to the present day (difficult to quantify) • Atmospheric isotopes – 40 Ar contains degassing record, integrated over Martian history ESS 250 Winter 2003

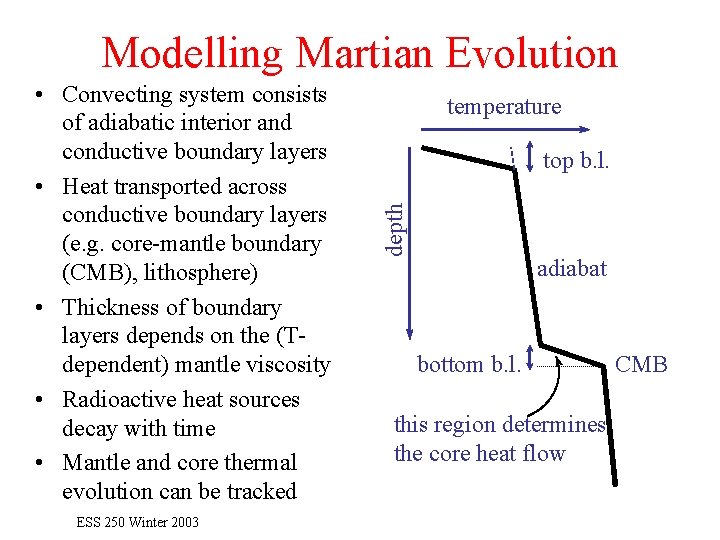
Modelling Martian Evolution ESS 250 Winter 2003 temperature top b. l. depth • Convecting system consists of adiabatic interior and conductive boundary layers • Heat transported across conductive boundary layers (e. g. core-mantle boundary (CMB), lithosphere) • Thickness of boundary layers depends on the (Tdependent) mantle viscosity • Radioactive heat sources decay with time • Mantle and core thermal evolution can be tracked adiabat bottom b. l. this region determines the core heat flow CMB

Core Behaviour (1) • The core needs to be convecting in order to produce a dynamo • The maximum heat flux it can get rid of without convection occurring is given by the adiabat: • Here k is conductivity, a is thermal expansivity, g is acceleration due to gravity, T is temperature and Cp is specific heat capacity. Typical Martian value ~15 m. W m-2 • The heat flux out of the core is controlled by the mantle’s ability to remove heat • If the heat flux out of the core drops below the critical value F then core convection will stop and the dynamo will cease ESS 250 Winter 2003

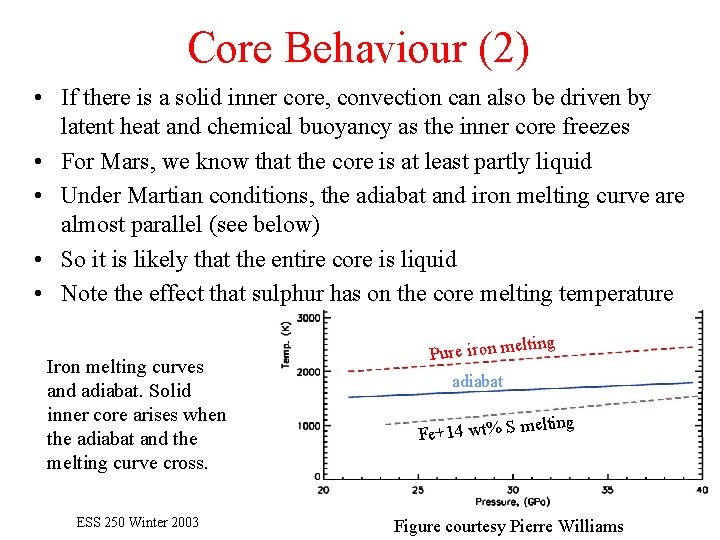
Core Behaviour (2) • If there is a solid inner core, convection can also be driven by latent heat and chemical buoyancy as the inner core freezes • For Mars, we know that the core is at least partly liquid • Under Martian conditions, the adiabat and iron melting curve are almost parallel (see below) • So it is likely that the entire core is liquid • Note the effect that sulphur has on the core melting temperature lting Iron melting curves and adiabat. Solid inner core arises when the adiabat and the melting curve cross. ESS 250 Winter 2003 Pure iron me adiabat Fe+14 wt% S m elting Figure courtesy Pierre Williams

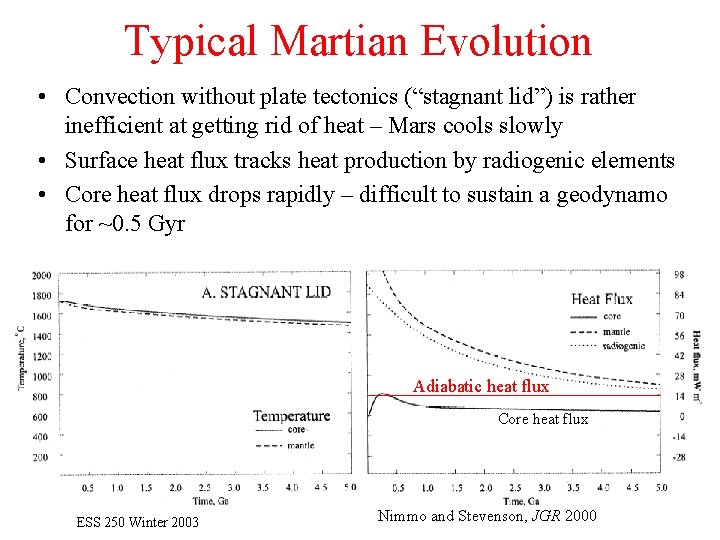
Typical Martian Evolution • Convection without plate tectonics (“stagnant lid”) is rather inefficient at getting rid of heat – Mars cools slowly • Surface heat flux tracks heat production by radiogenic elements • Core heat flux drops rapidly – difficult to sustain a geodynamo for ~0. 5 Gyr Adiabatic heat flux Core heat flux ESS 250 Winter 2003 Nimmo and Stevenson, JGR 2000

Sustaining a geodynamo? • To sustain a geodynamo we need some way of increasing the heat flux out of the core. Several possibilities: • 1) Plate tectonics – mantle cools faster, which means that more heat is extracted from the core. When plate tectonics stops, the geodynamo will also cease. Unfortunately, not clear that plate tectonics ever happened. . . • 2) Potassium in the core – acts as an additional heat source. But the half-life of potassium is long (1. 25 Gyr) – means that the dynamo lasts too long • 3) A hot core – when the core differentiates it is likely to end up hotter than the mantle (gravitational energy). A hot core will increase the core heat flux temporarily, and can sustain a geodynamo for 0. 5 Gyr. ESS 250 Winter 2003

Summary • SNC chemistry and surface measurements can be used to infer bulk and surface composition of Mars • Observations of spacecraft orbit and planetary precession can be used to derive moment of inertia and thus internal structure • Gravity and topography can be used to infer lithospheric rigidity, density and crustal thickness (admittance technique) • Variations in lithospheric rigidity with time can be used to infer change in heat flux • Magnetic observations give indication of depth of magnetized layer and suggest dynamo only lasted for first ~0. 5 Gyr • Sustaining a dynamo for this length of time may require either a hot core or an episode of plate tectonics • Both gravity and magnetic resolution are limited by the altitude of the spacecraft ESS 250 Winter 2003