ESK VYSOK UEN TECHNICK V PRAZE FAKULTA STROJN

ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STROJNÍ Numerické řešení stlačitelného proudění v kanále a mříži Autor: Milan ŽALOUDEK Vedoucí práce: Doc. Ing. Jaroslav FOŘT, CSc.

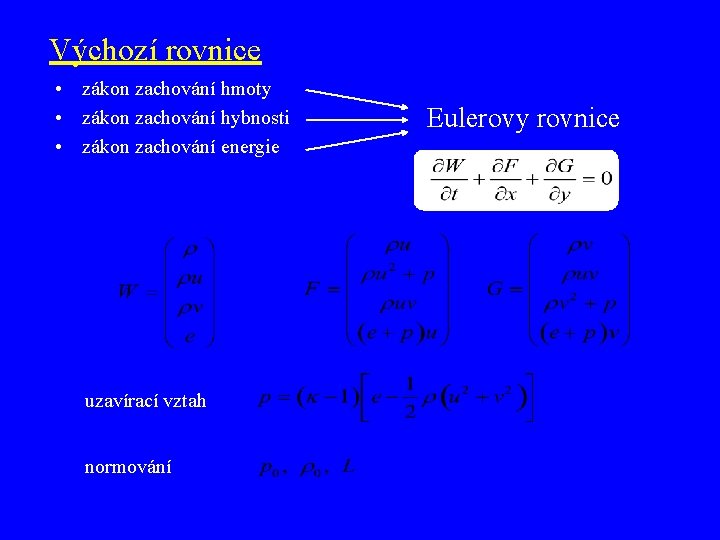
Výchozí rovnice • zákon zachování hmoty • zákon zachování hybnosti • zákon zachování energie uzavírací vztah normování Eulerovy rovnice

Matematická formulace úlohy systém nelineárních hyperbolických rovnic slabé řešení hledáme funkci W(x, y, t) na oblasti 2 + : • W K( ) – třída funkcí, ve které připouštíme existenci spočetně mnoha křivek, podél nichž funkce W nabývá různých konečných limitních hodnot zleva a zprava tyto křivky nazýváme rázové vlny popř. nespojitosti I. druhu mimo tyto křivky je funkce W spojitá • W splňuje rovnici pro libovolné t 2>t 1 a libovolnou oblast D s dostatečně hladkou hranicí • W splňuje počáteční podmínky W(t=0)=W 0 • W splňuje okrajové podmínky

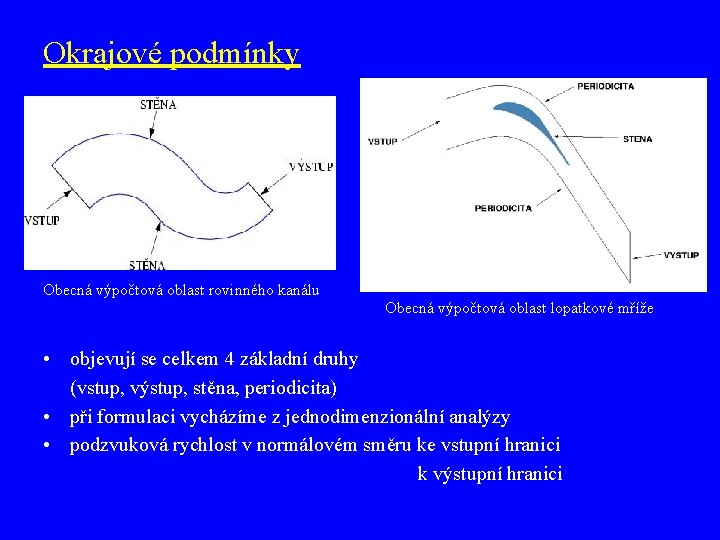
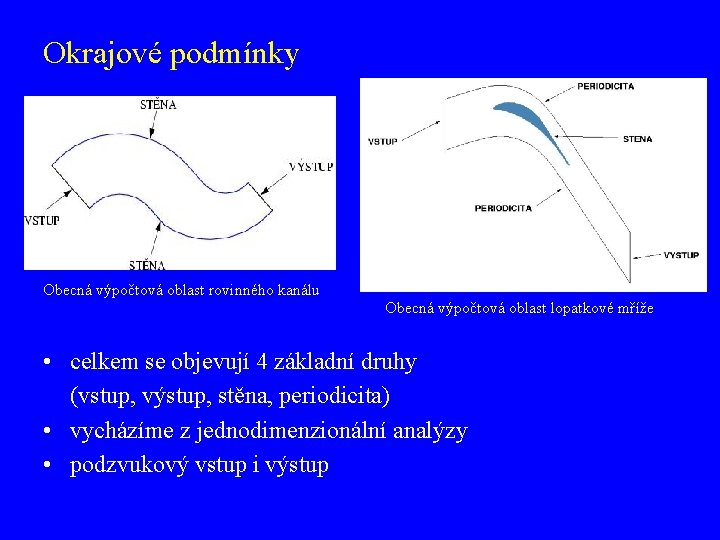
Okrajové podmínky Obecná výpočtová oblast rovinného kanálu Obecná výpočtová oblast lopatkové mříže • objevují se celkem 4 základní druhy (vstup, výstup, stěna, periodicita) • při formulaci vycházíme z jednodimenzionální analýzy • podzvuková rychlost v normálovém směru ke vstupní hranici k výstupní hranici

Numerické řešení úlohy • cell-centered (hodnoty proměnných v těžišti objemu) diskretizace základních rovnic: R: obdélníkové pravidlo numerického integrování L: Eulerova dopředná aproximace • výpočtová oblast je pokryta strukturovanou čtyřúhelníkovou sítí

Aproximace toku v 1 D pomocí numerické metody AUSM = zkratka ang. Advection Upstream Splitting Method schéma je založeno na struktuře řešení Riemannova problému Eulerovy rovnice v 1 D: vlastní čísla Machovo číslo , kde rozhoduje o druhu režimu a o počtu kladných a záporných vlastních čísel tok F rozdělíme na advektivní a tlakovou část dále upravíme tento tok aproximujeme pomocí hodnot z L a R jako jejich vhodnou kombinaci proto použité hodnoty formálně přeznačíme

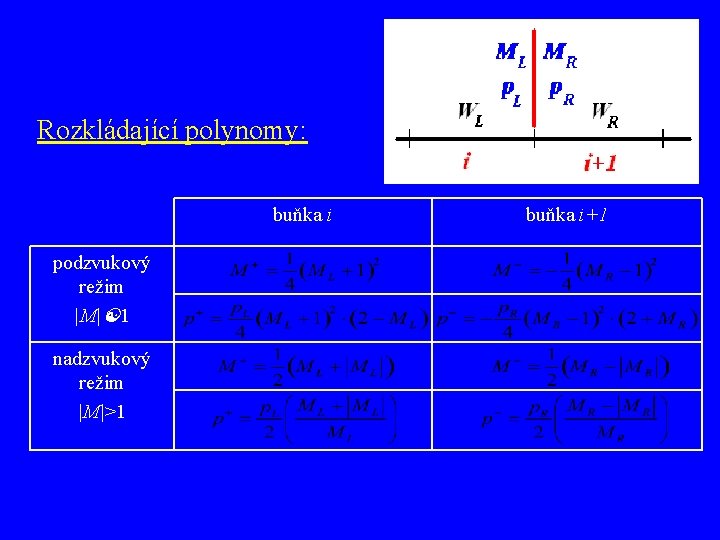
Aproximace toku F na hranici mezi i-tou a (i+1)-ní buňkou k určení MLR , p. LR používáme tzv. rozkládající (splitting) polynomy Označení rozkládajících polynomů buňka i+1 Machova čísla tlaku v každé buňce vyčíslíme jednotlivé polynomy a jejich následnou kombinací získáme MLR a p. LR Požadavky na rozkládající polynomy (platí stejně pro M+/- i p+/-): • M+ , M- spolu se svými prvními derivacemi spojitě závislé na Machově čísle • vyjádřeny polynomem nejnižšího možného stupně • vlastní čísla jsou kladná, vlastní čísla jsou záporná výraz LR je dán proměnnými pouze jedné hraniční buňky a to podle znaménka výsledného MLR

Rozkládající polynomy: buňka i podzvukový režim |M|<1 nadzvukový režim |M|>1 buňka i+1

Rozšíření numerického schématu na 2 D • • zavedeme kladnou orientaci hran (a, b) vektor jednotkové vnější normály • aproximovaný numerický tok přepíšeme • zavedeme matici rotace • Eulerovy rovnice jsou invariantní vůči rotaci dvourozměrný případ je založen na jednodimenzionálním rozkladu v normálovém směru • o režimu proudění rozhoduje Machovo číslo v normálovém směru

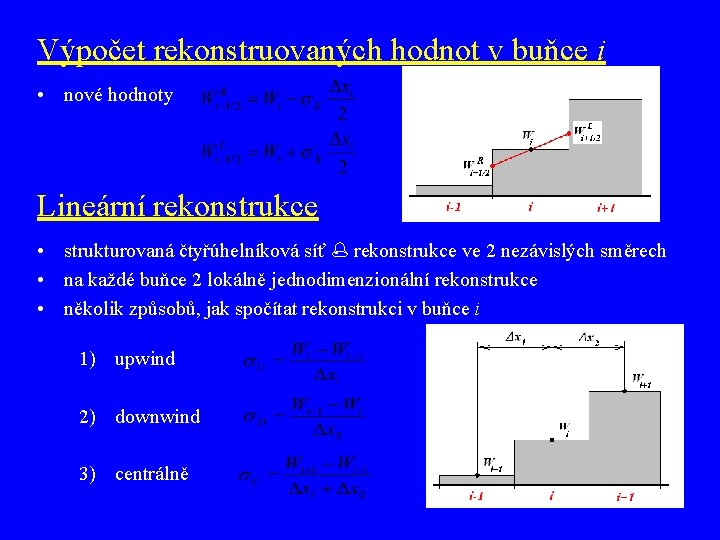
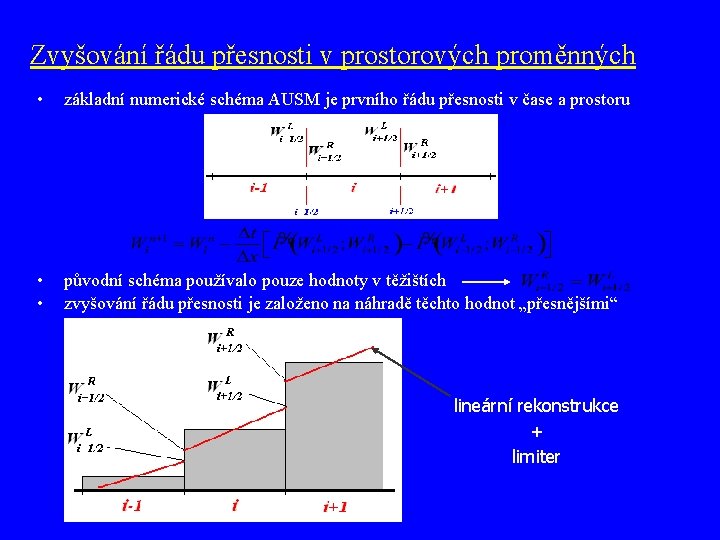
Zvyšování řádu přesnosti v prostorových proměnných • základní numerické schéma AUSM je prvního řádu přesnosti v prostoru • původní schéma používalo pouze hodnoty v těžištích • zvyšování řádu přesnosti je založeno na náhradě těchto hodnot „přesnějšími“ lineární rekonstrukce + limiter

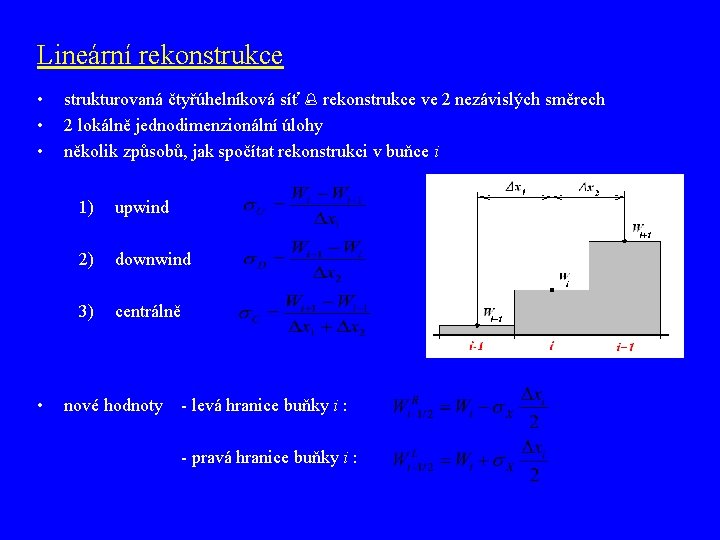
Výpočet rekonstruovaných hodnot v buňce i • nové hodnoty Lineární rekonstrukce • strukturovaná čtyřúhelníková síť rekonstrukce ve 2 nezávislých směrech • na každé buňce 2 lokálně jednodimenzionální rekonstrukce • několik způsobů, jak spočítat rekonstrukci v buňce i 1) upwind 2) downwind 3) centrálně

Limitery (omezovače) od prováděných úprav požadujeme neoscilativní chování rekonstruované hodnoty na hranici i-1/2 musí ležet mezi Wi-1 a Wi rekonstruované hodnoty na hranici i+1/2 musí ležet mezi Wi a Wi+1 samotná rekonstrukce 1), 2) nebo 3) nezaručí neoscilativní chování doplnění o vhodný limiter definujme funkce minmod a maxmod minmod limiter MC limiter superbee limiter Barthův limiter speciální úprava rekonstrukce v okrajových buňkách

Numerická aproximace okrajových podmínek Předpokládáme: pracovní médium uloženo ve velkém zásobníku ze zásobníku dopraveno izoentropicky na vstupní hranici proudění výpočtovou oblastí výstup do prostředí se známým tlakem VSTUP + VÝSTUP - podle druhu zadáme vždy vhodný počet parametrů - zbývající veličiny extrapolujeme ze 2 sousedních buněk STĚNA - podmínka neprostupnosti stěny PERIODICITA - periodická hranice má regulární buňky na obou stranách - numerický tok počítáme podle vzorce pro regulární hranici

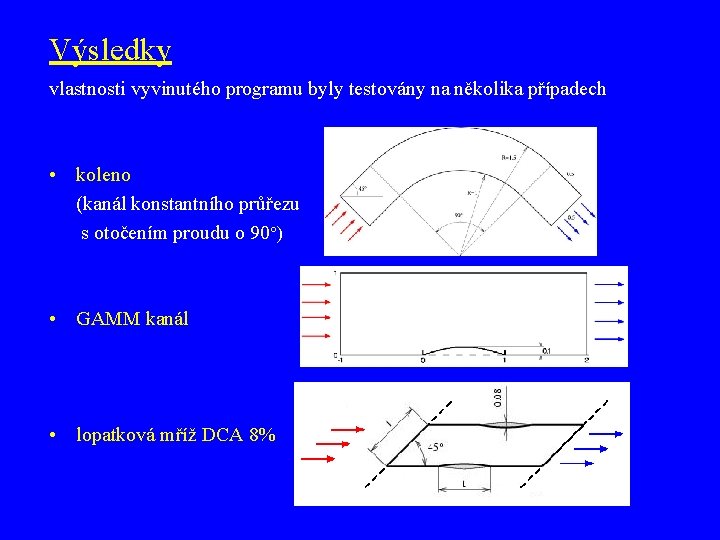
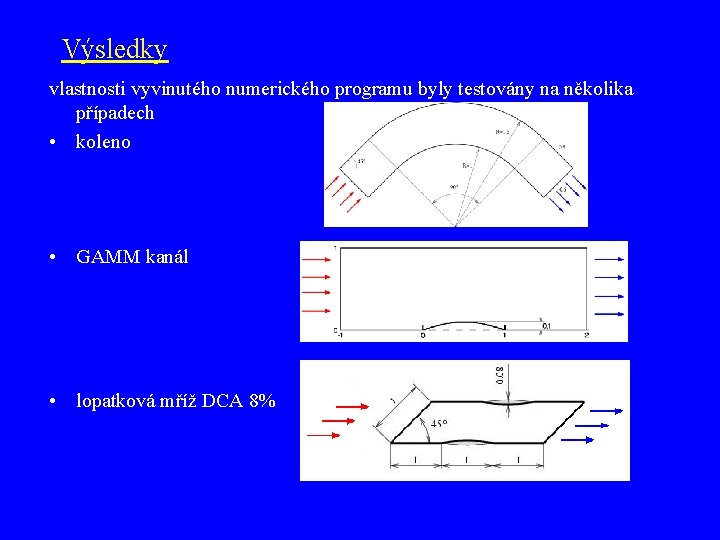
Výsledky vlastnosti vyvinutého programu byly testovány na několika případech • koleno (kanál konstantního průřezu s otočením proudu o 90 ) • GAMM kanál • lopatková mříž DCA 8%

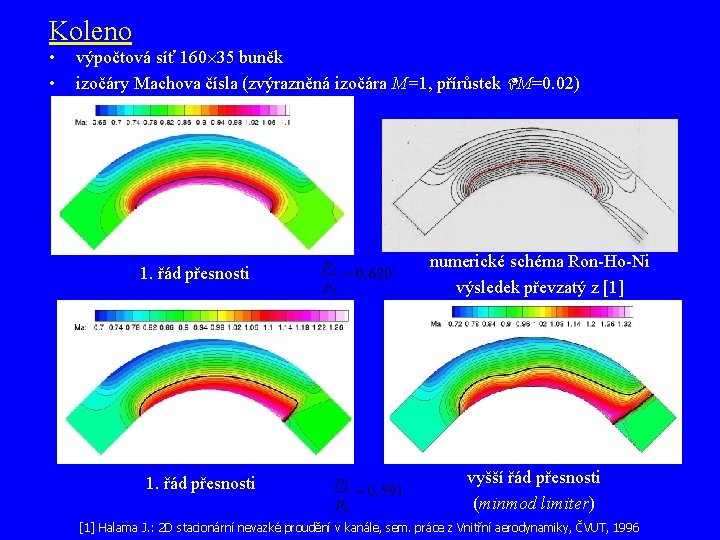
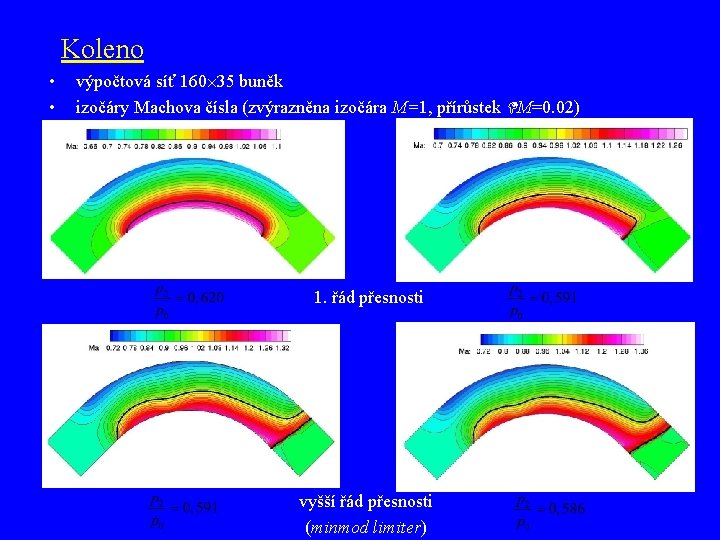
Koleno • • výpočtová síť 160 35 buněk izočáry Machova čísla (zvýrazněná izočára M=1, přírůstek M=0. 02) 1. řád přesnosti numerické schéma Ron-Ho-Ni výsledek převzatý z [1] vyšší řád přesnosti (minmod limiter) [1] Halama J. : 2 D stacionární nevazké proudění v kanále, sem. práce z Vnitřní aerodynamiky, ČVUT, 1996

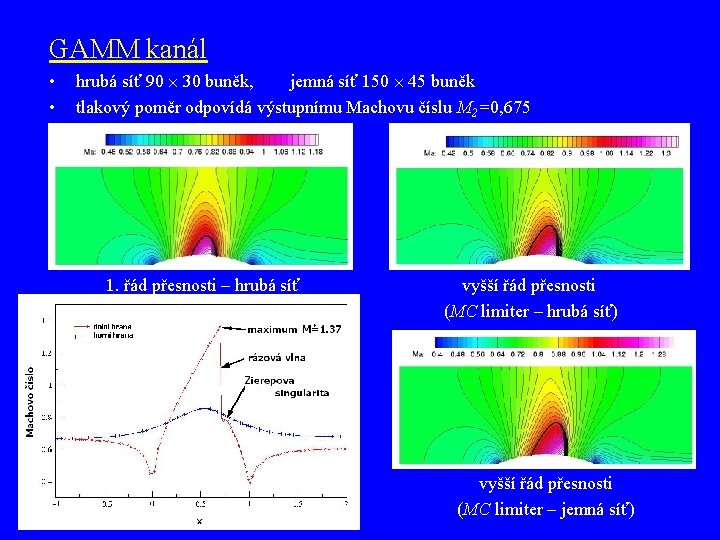
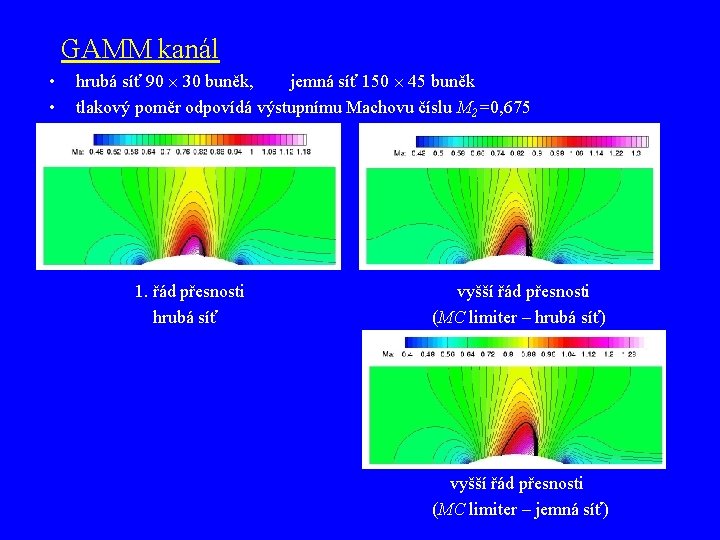
GAMM kanál • • hrubá síť 90 30 buněk, jemná síť 150 45 buněk tlakový poměr odpovídá výstupnímu Machovu číslu M 2=0, 675 1. řád přesnosti – hrubá síť vyšší řád přesnosti (MC limiter – hrubá síť) vyšší řád přesnosti (MC limiter – jemná síť)

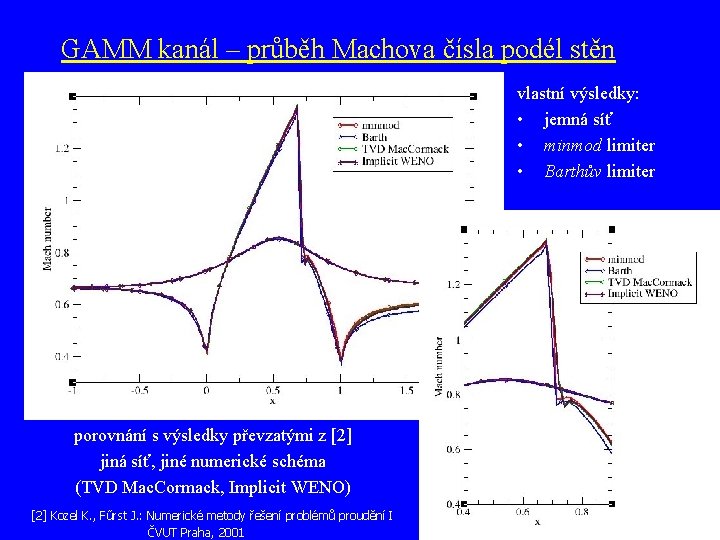
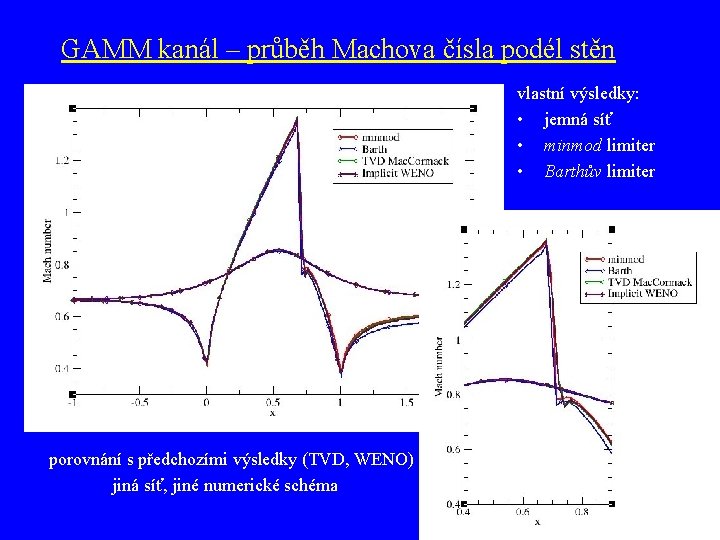
GAMM kanál – průběh Machova čísla podél stěn vlastní výsledky: • jemná síť • minmod limiter • Barthův limiter porovnání s výsledky převzatými z [2] jiná síť, jiné numerické schéma (TVD Mac. Cormack, Implicit WENO) [2] Kozel K. , Fűrst J. : Numerické metody řešení problémů proudění I ČVUT Praha, 2001

lopatková mříž DCA 8% Parametry výpočtu: • vyšší řád přesnosti s minmod limiterem • výpočtová síť 120 40 buněk • tlakový poměr odpovídá výstupnímu Machovu číslu M 2=0, 833 • úhel nabíhajícího proudu =0, 9

Závěr Cílem práce bylo vyvinout a odladit vlastní numerický program, pro řešení nevazkého stlačitelného proudění, založený na numerickém schématu AUSM. Tento cíl byl splněn. Dosahované výsledky jsou ve shodě s jinými numerickými výsledky i s fyzikálními předpoklady proudění. Další vývoj programu: • implementace a testování dalších variant AUSM schématu • přechod na stlačitelné vazké proudění • rozšíření na 3 D úlohy

Děkuji za pozornost

Děkuji za pozornost

Výchozí rovnice • zákon zachování hmoty • zákon zachování hybnosti hustota rychlost energie tlak • zákon zachování energie tečné napětí objemová síla hustota objemového toku rychlost deformace čas

zjednodušující předpoklady • • rovinné proudění nevazká tekutina nulové hmotové síly žádné zdroje tepla Eulerovy rovnice: uzavírací vztah normování

Matematická formulace úlohy systém nelineárních hyperbolických rovnic slabé řešení hledáme funkci W(x, y, t) na oblasti 2 + : • W K( ) • W splňuje rovnici pro libovolné t 2>t 1 a libovolnou oblast D s dostatečně hladkou hranicí • W splňuje počáteční podmínky W(t=0)=W 0 • W splňuje okrajové podmínky

Okrajové podmínky Obecná výpočtová oblast rovinného kanálu Obecná výpočtová oblast lopatkové mříže • celkem se objevují 4 základní druhy (vstup, výstup, stěna, periodicita) • vycházíme z jednodimenzionální analýzy • podzvukový vstup i výstup

Numerické řešení úlohy • metoda konečných objemů (FVM) • cell-centered (hodnoty proměnných v těžišti objemu) R: obdélníkové pravidlo numerického integrování L: Eulerova dopředná aproximace • výpočtová oblast je pokryta strukturovanou čtyřúhelníkovou sítí suma na R straně je aproximována pomocí numerického schématu

Numerické schéma AUSM v 1 D AUSM = zkratka ang. Advection Upstream Splitting Method schéma je založeno na struktuře řešení Riemannova problému Eulerovy rovnice v 1 D: vlastní čísla Machovo číslo , kde rozhoduje o druhu režimu a o počtu kladných a záporných vlastních čísel tok F rozdělíme na advektivní a tlakovou část dále upravíme tento tok aproximujeme pomocí hodnot z L a R jako jejich vhodnou kombinaci proto použité hodnoty formálně přeznačíme

Aproximace toku F na hranici mezi i-tou a (i+1)-ní buňkou k určení MLR , p. LR používáme tzv. rozkládající (splitting) polynomy Označení rozkládajících polynomů buňka i+1 Machova čísla M+ M- tlaku p+ p- v každé buňce vyčíslíme jednotlivé polynomy a jejich následnou kombinací získáme MLR a p. LR Požadavky na rozkládající polynomy (platí stejně pro M+/- i p+/-): • • M+ , M- spolu se svými prvními derivacemi vyjádřeny polynomem nejnižšího možného stupně • vlastní čísla jsou kladná, vlastní čísla spojitě závislé na Machově čísle jsou záporná výraz LR, je dán proměnnými pouze jedné hraniční buňky a to podle znaménka výsledného MLR

Rozkládající polynomy: buňka i podzvukový režim |M| 1 nadzvukový režim |M|>1 buňka i+1

Rozšíření numerického schématu na 2 D • • zavedeme kladnou orientaci hran (a, b) vektor jednotkové vnější normály • aproximovaný numerický tok přepíšeme • zavedeme matici rotace • Eulerovy rovnice jsou invariantní vůči rotaci dvourozměrný případ je založen na jednodimenzionálním rozkladu v normálovém směru • o režimu proudění rozhoduje Machovo číslo v normálovém směru

Numerická aproximace okrajových podmínek VSTUP - médium uloženo ve velkém zásobníku, kde má klidové parametry p 0, 0 - ze zásobníku dopraveno izoentropicky na vstupní hranici - zadáváme klidové parametry p 0, úhel náběhu - z proudového pole extrapolujeme Machovo číslo Min

Numerická aproximace okrajových podmínek VÝSTUP - médium vystupuje z výpočtové oblasti do prostředí se známým tlakem p 2 - tento tlak je dán poměrem - z proudového pole extrapolujeme první 3 složky vektoru W - zadáváme tlakový poměr - čtvrtou složku W dopočítáme podle STĚNA - idealizovaný model nevazké stěny (žádná mezní vrstva, rychlostní profil. . . ap. ) - podmínka neprostupnosti stěny po úpravách - tlak na stěně pwall nahrazujeme tlakem v nejbližší buňce přilehlé ke stěně PERIODICITA - periodická hranice má regulární buňky na obou stranách - numerický tok počítáme podle vzorce pro regulární hranici

Zvyšování řádu přesnosti v prostorových proměnných • základní numerické schéma AUSM je prvního řádu přesnosti v čase a prostoru • • původní schéma používalo pouze hodnoty v těžištích zvyšování řádu přesnosti je založeno na náhradě těchto hodnot „přesnějšími“ lineární rekonstrukce + limiter

Lineární rekonstrukce • • strukturovaná čtyřúhelníková síť rekonstrukce ve 2 nezávislých směrech 2 lokálně jednodimenzionální úlohy několik způsobů, jak spočítat rekonstrukci v buňce i 1) upwind 2) downwind 3) centrálně nové hodnoty - levá hranice buňky i : - pravá hranice buňky i :

Limitery požadujeme neoscilativní chování rekonstruované hodnoty na hranici i-1/2 musí ležet mezi Wi-1 a Wi rekonstruované hodnoty na hranici i+1/2 musí ležet mezi Wi a Wi+1 samotná rekonstrukce 1), 2) nebo 3) nezaručí neoscilativní chování doplnění o vhodný limiter definujme funkce minmod a maxmod minmod limiter MC limiter superbee limiter Barthův limiter

Rekonstrukce s použitím minmod limiteru Porovnání rekonstrukcí s různými limitery Rekonstrukce v okrajových buňkách • • předpokládáme, že hodnota daná okrajovou podmínkou je přesná není třeba ji upravovat hodnota na okrajových hranách je bez rekonstrukce na následující hraně používáme jednostrannou rekonstrukci bez limiteru

Výsledky vlastnosti vyvinutého numerického programu byly testovány na několika případech • koleno • GAMM kanál • lopatková mříž DCA 8%

Koleno • • výpočtová síť 160 35 buněk izočáry Machova čísla (zvýrazněna izočára M=1, přírůstek M=0. 02) 1. řád přesnosti vyšší řád přesnosti (minmod limiter)

GAMM kanál • • hrubá síť 90 30 buněk, jemná síť 150 45 buněk tlakový poměr odpovídá výstupnímu Machovu číslu M 2=0, 675 1. řád přesnosti hrubá síť vyšší řád přesnosti (MC limiter – hrubá síť) vyšší řád přesnosti (MC limiter – jemná síť)

GAMM kanál – průběh Machova čísla podél stěn vlastní výsledky: • jemná síť • minmod limiter • Barthův limiter porovnání s předchozími výsledky (TVD, WENO) jiná síť, jiné numerické schéma

lopatková mříž DCA 8% Parametry výpočtu: • vyšší řád přesnosti s minmod limiterem • výpočtová síť 120 40 buněk • tlakový poměr odpovídá výstupnímu Machovu číslu M 2=0, 833 • úhel nabíhajícího proudu =0, 9