Esercizio rappresentare con una rete di Petri il

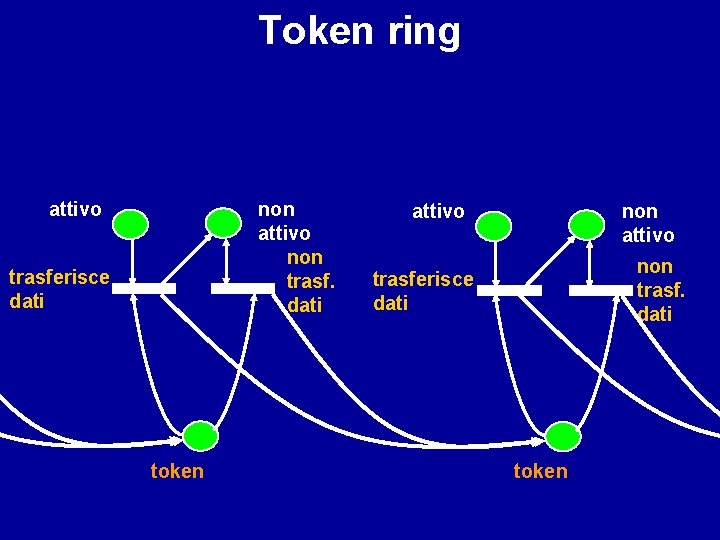
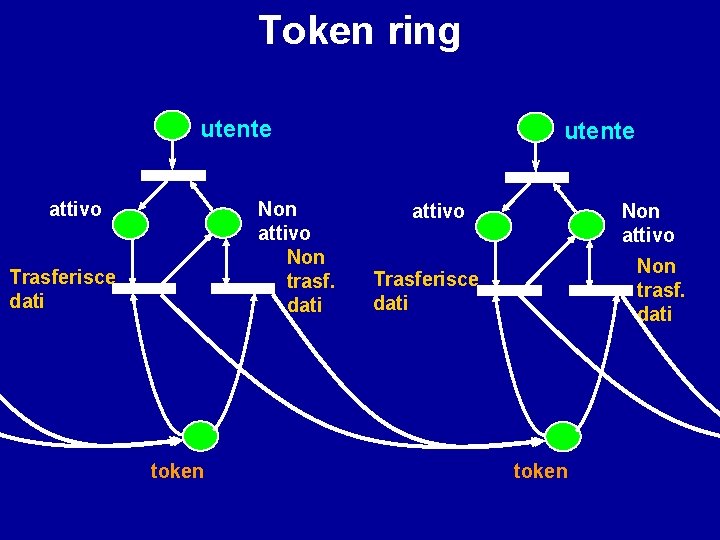
Esercizio: rappresentare con una rete di Petri il seguente protocollo di comunicazione: ciascun utente in modo ciclico trasferisce dati e/o passa la comunicazione all’utente successivo

Token ring attivo non trasf. dati trasferisce dati token

Token ring utente attivo Non trasf. dati Trasferisce dati token

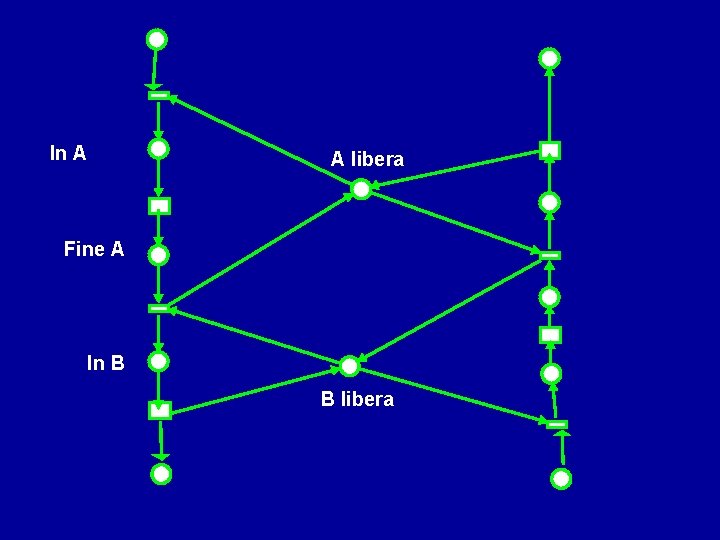
Esercizio: rappresentare un senso unico alternato costituito da due tratte stradali senza visibilità reciproca (reciprocamente dietro un angolo); introdurre uno o più tipi di controllo con semafori ai due ingressi e rappresentarli

In A A libera Fine A In B B libera

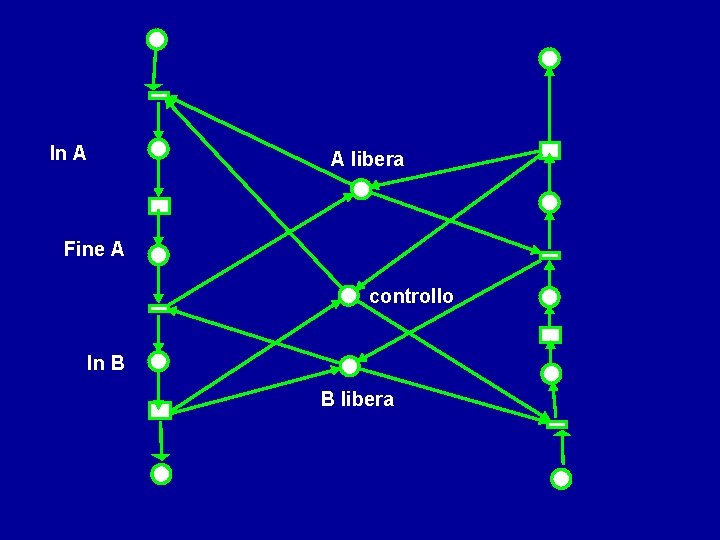
In A A libera Fine A controllo In B B libera

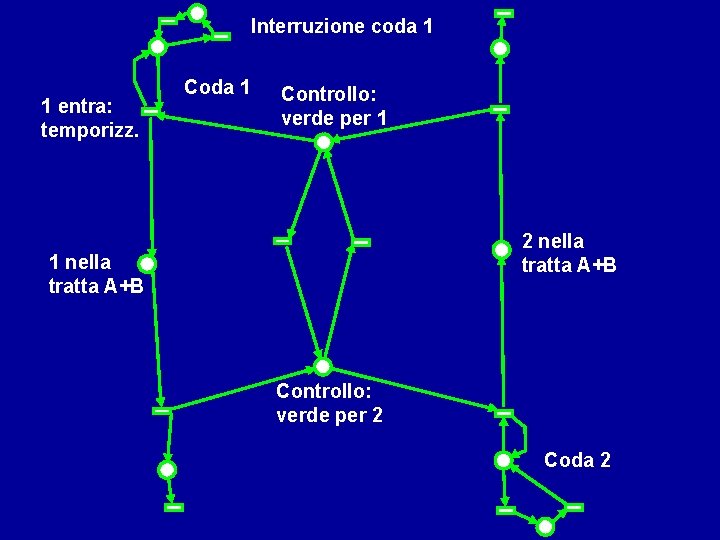
Interruzione coda 1 1 entra: temporizz. Coda 1 Controllo: verde per 1 2 nella tratta A+B 1 nella tratta A+B Controllo: verde per 2 Coda 2

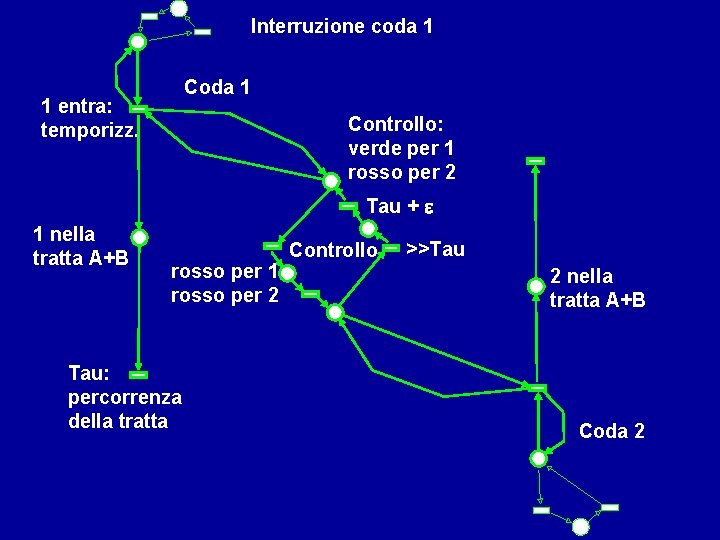
Interruzione coda 1 Coda 1 1 entra: temporizz. Controllo: verde per 1 rosso per 2 Tau + e 1 nella tratta A+B rosso per 1 rosso per 2 Tau: percorrenza della tratta Controllo >>Tau 2 nella tratta A+B Coda 2

2. 5 Invarianti di posto, di transizione; grafi di sincronizzazione; controllo supervisore di una macchina: invarianti

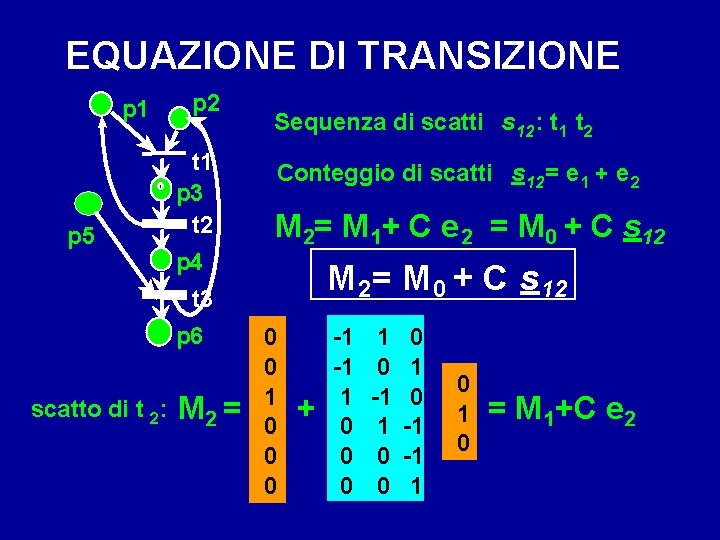
EQUAZIONE DI TRANSIZIONE p 1 p 5 p 2 t 1 p 3 t 2 Sequenza di scatti s 12: t 1 t 2 Conteggio di scatti s 12= e 1 + e 2 M 2= M 1+ C e 2 = M 0 + C s 12 p 4 M 2= M 0 + C s 12 t 3 p 6 scatto di t 2: M 2 = 0 0 1 0 0 0 + -1 -1 1 0 0 0 1 0 -1 -1 1 0 = M 1+C e 2

Struttura delle Reti di Petri P-INVARIANTI Un invariante di posto è un vettore riga definito positivo* che annulla la matrice di incidenza X 0: XC = 0 XMi= XM 0 + XC s XMi = XM 0 * con almeno una componente positiva e le altre positive o nulle

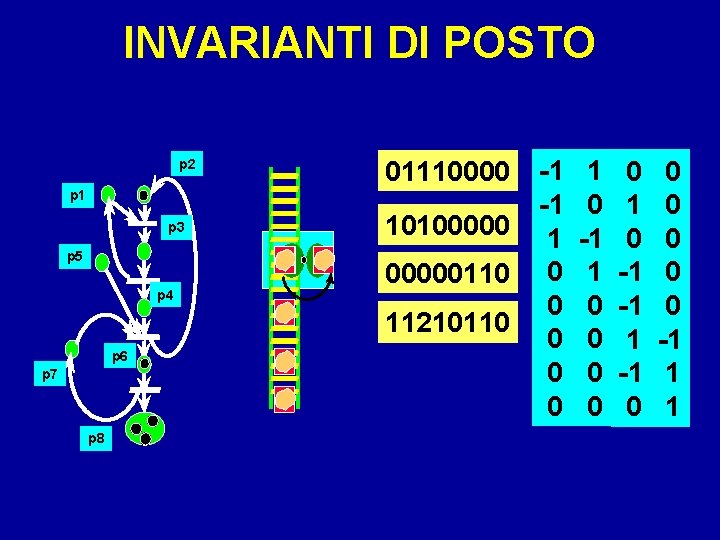
INVARIANTI DI POSTO p 2 01110000 p 1 p 3 p 5 p 4 10100000110 11210110 p 6 p 7 p 8 -1 -1 1 0 0 0 0 0 1 0 -1 -1 0 0 0 -1 1 1

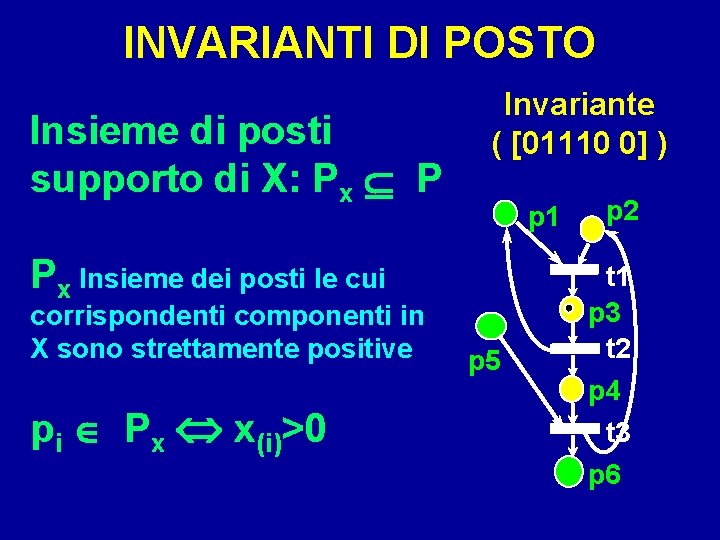
INVARIANTI DI POSTO Insieme di posti supporto di X: Px P Invariante ( [01110 0] ) p 1 Px Insieme dei posti le cui corrispondenti componenti in X sono strettamente positive pi Px x(i)>0 p 5 p 2 t 1 p 3 t 2 p 4 t 3 p 6

P-INVARIANTI I p-invarianti sono caratterizzati graficamente da una sottorete N’ Invariante ( [01110 0] ) p 1 N’ = (Px, T’, A’) - T’ transizioni collegate con posti di Px - A’ A = (P X T) (T X P) - A’ = (Px X T’) (T’ X Px) p 5 p 2 t 1 p 3 t 2 p 4 t 3 p 6

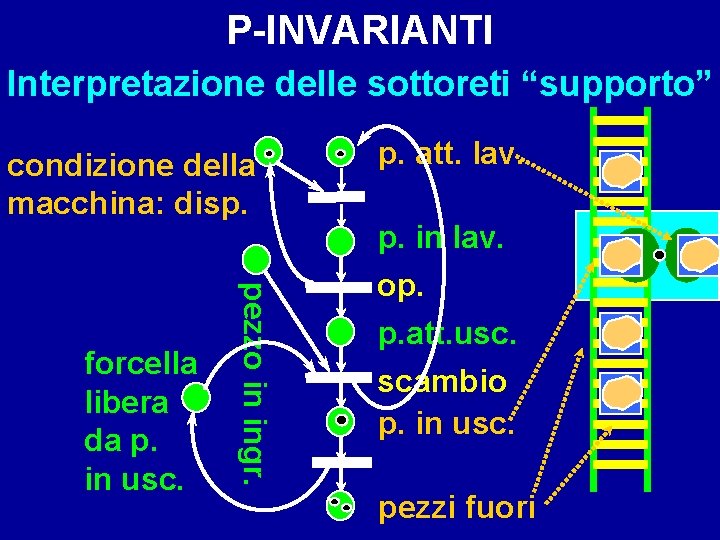
P-INVARIANTI Interpretazione delle sottoreti “supporto” condizione della macchina: disp. pezzo in ingr. forcella libera da p. in usc. p. att. lav. p. in lav. op. p. att. usc. scambio p. in usc. pezzi fuori

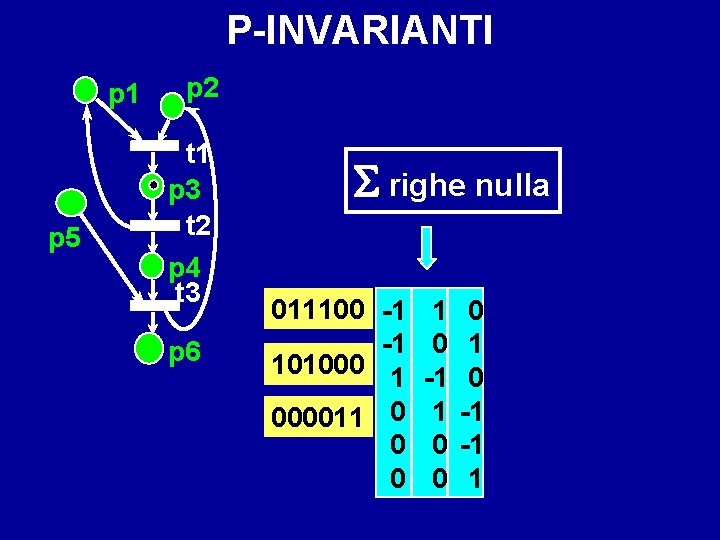
P-INVARIANTI p 1 p 5 p 2 t 1 p 3 t 2 p 4 t 3 p 6 righe nulla 011100 -1 -1 101000 1 000011 0 0 0 1 0 -1 -1 1

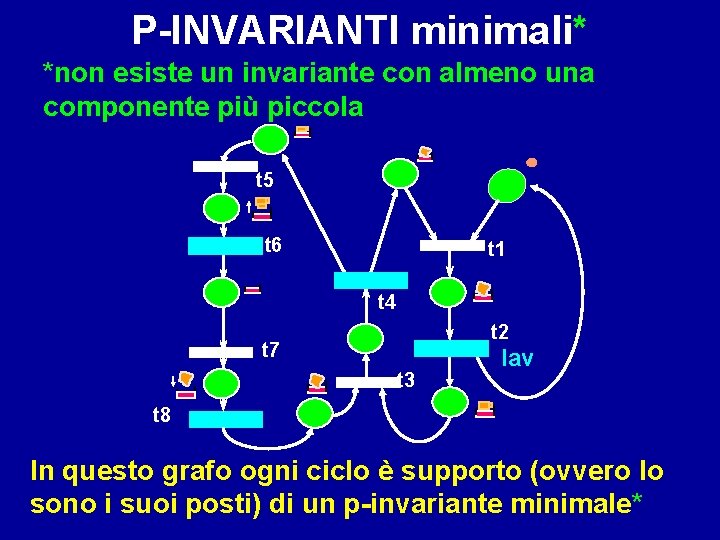
P-INVARIANTI minimali* *non esiste un invariante con almeno una componente più piccola t 5 t 6 t 1 t 4 t 2 t 7 t 3 lav t 8 In questo grafo ogni ciclo è supporto (ovvero lo sono i suoi posti) di un p-invariante minimale*

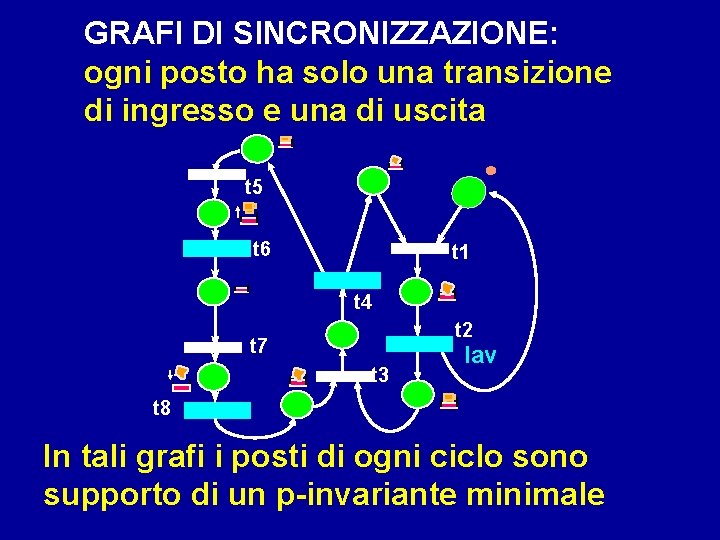
GRAFI DI SINCRONIZZAZIONE: ogni posto ha solo una transizione di ingresso e una di uscita t 5 t 6 t 1 t 4 t 2 t 7 t 3 lav t 8 In tali grafi i posti di ogni ciclo sono supporto di un p-invariante minimale

GRAFI DI SINCRONIZZAZIONE: ogni ciclo è supporto di un p-invariante minimale Ogni riga (posto p*) ha un solo 1 (nella colonna t*-in) e un solo -1 (nella t*-out) Nel ciclo, p* ha un solo predecessore, la relativa riga ha -1 nella t*-in, e un solo successore e la relativa riga ha 1 nella t*-out

GRAFI DI SINCRONIZZAZIONE: ogni ciclo è supporto di un p-invariante minimale Di conseguenza la somma delle righe dei posti del ciclo è nulla e quindi il ciclo è supporto di un invariante L'invariante è minimale, infatti l’esclusione di una o più righe rende la somma non nulla

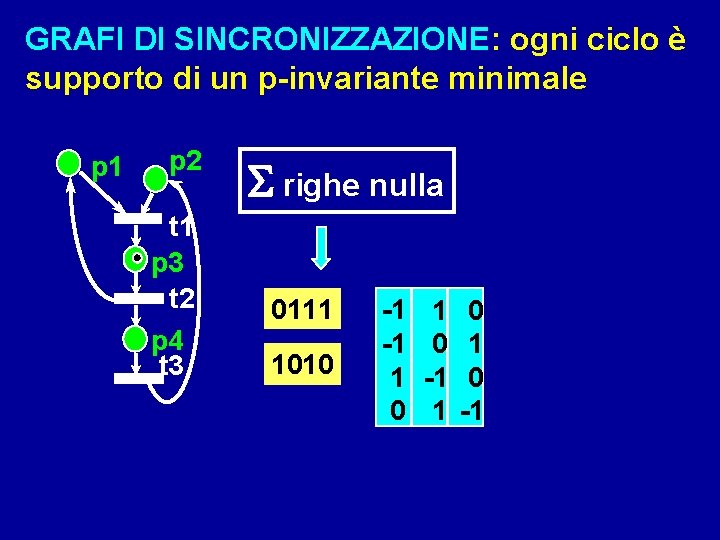
GRAFI DI SINCRONIZZAZIONE: ogni ciclo è supporto di un p-invariante minimale p 1 p 2 t 1 p 3 t 2 p 4 t 3 righe nulla 0111 1010 -1 -1 1 0 1 0 -1

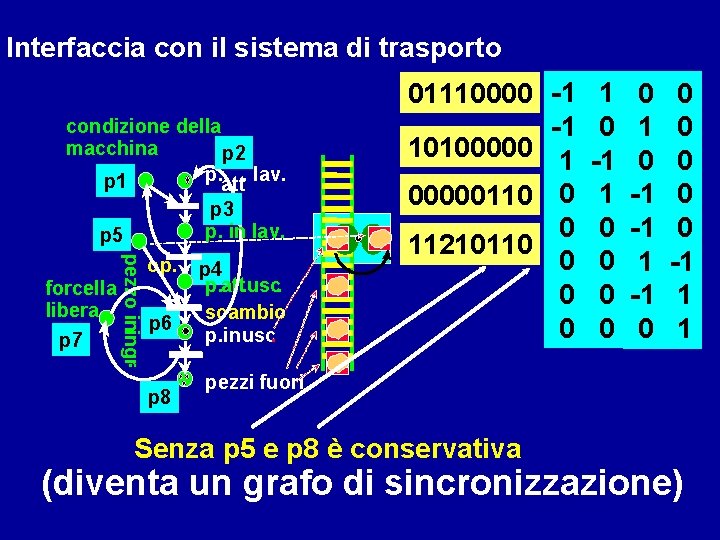
Interfaccia con il sistema di trasporto condizione della macchina p 2 p. att. lav. p 1 p 3 p. in lav. p 5 pezzo iningr. forcella libera p 7 op. p 6 p 8 p 4 p. att. usc. scambio p. in usc. 01110000 -1 -1 10100000 1 00000110 0 0 11210110 0 1 0 -1 1 0 0 0 1 0 -1 -1 0 0 0 -1 1 1 pezzi fuori Senza p 5 e p 8 è conservativa (diventa un grafo di sincronizzazione)

P-INVARIANTI Gli invarianti di due sottoreti con posti in comune (ma non transizioni) sono la traccia degli invarianti della rete globale e viceversa questi sono la composizione di quelli C X 1 1 1 -1 1 0 0 1 -1 X’ C’ 1 1 -1 X” C” 3 1 1 1 -1 1 1 3 2 1 -1 2 4

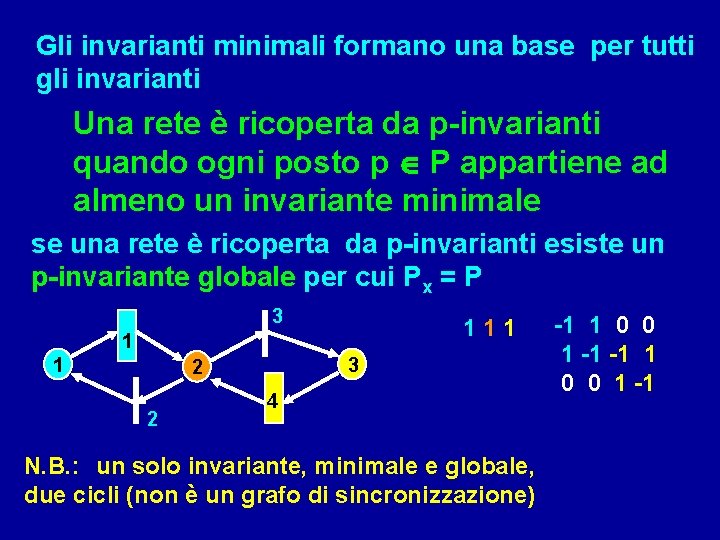
Gli invarianti minimali formano una base per tutti gli invarianti Una rete è ricoperta da p-invarianti quando ogni posto p P appartiene ad almeno un invariante minimale se una rete è ricoperta da p-invarianti esiste un p-invariante globale per cui Px = P 3 111 1 1 3 2 2 4 N. B. : un solo invariante, minimale e globale, due cicli (non è un grafo di sincronizzazione) -1 1 0 0 1 -1

Proprietà dei Grafi di sincronizzazione Un grafo di sincronizzazione marcato è vivo se ogni ciclo contiene almeno una marca

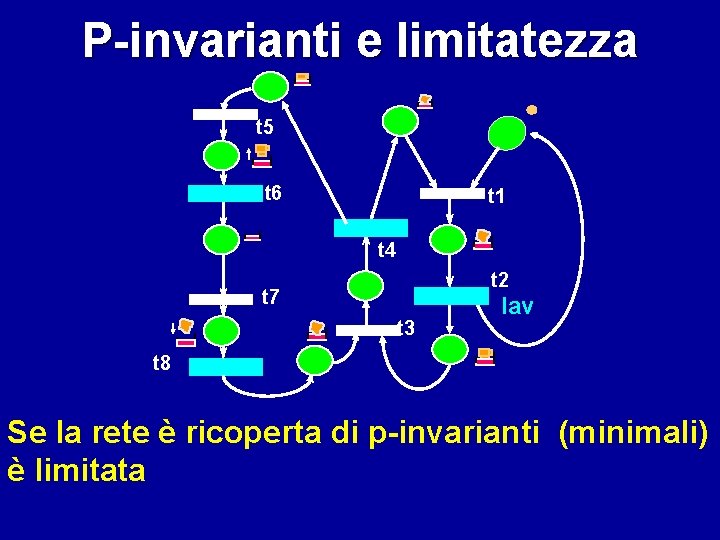
P-invarianti e limitatezza t 5 t 6 t 1 t 4 t 2 t 7 t 3 lav t 8 Se la rete è ricoperta di p-invarianti (minimali) è limitata

P-invarianti e conservatività Se esiste un t 5 invariante globale° la rete è t 6 conservativa per t 4 W=2 ogni marcatura W=2 t 7 iniziale con lo t 3 stesso peso * w (e t 8 viceversa? ) °con x>0: x. Mi = x. M 0 + x. Cs = x. M 0 per ogni possibile M 0 e s *in questo caso la rete si dice strutturalmente conservativa t 1 t 2 lav

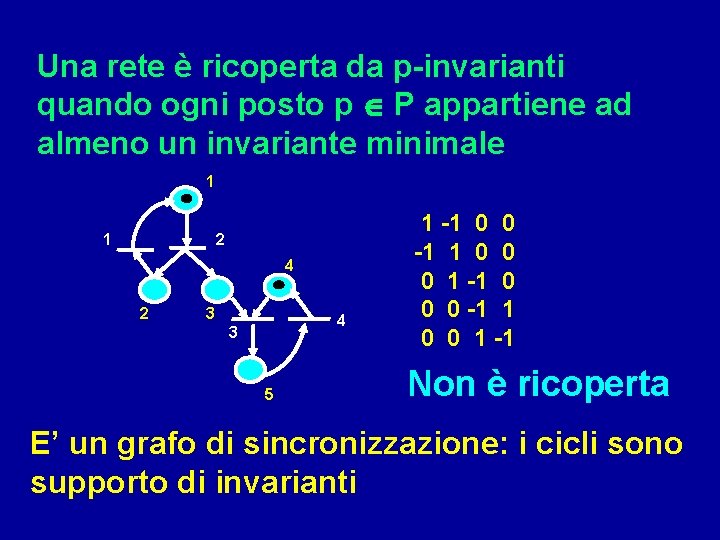
Una rete è ricoperta da p-invarianti quando ogni posto p P appartiene ad almeno un invariante minimale 1 1 2 4 2 3 4 3 5 1 -1 0 0 -1 1 0 0 0 1 -1 0 0 0 -1 1 0 0 1 -1 Non è ricoperta E’ un grafo di sincronizzazione: i cicli sono supporto di invarianti

Algoritmo di Alaiwan-Toudic Serve a determinare gli invarianti minimali Con trasformazioni matriciali si riducono progressivamente le dimensioni fino a trovare le soluzioni intere positive minime di XC=0

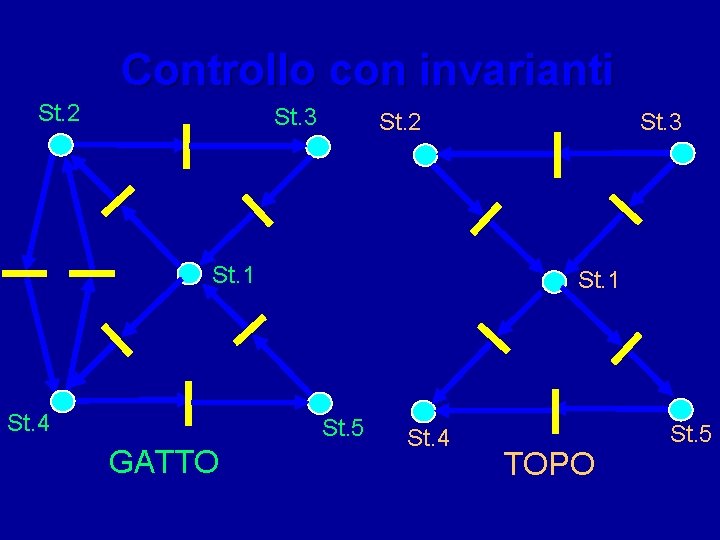
Controllo con invarianti Costruendo un invariante con un posto del controllo si può imporre il valore della somma delle marche in assegnati posti del processo controllato Ciò può corrispondere a specifiche significative per il processo

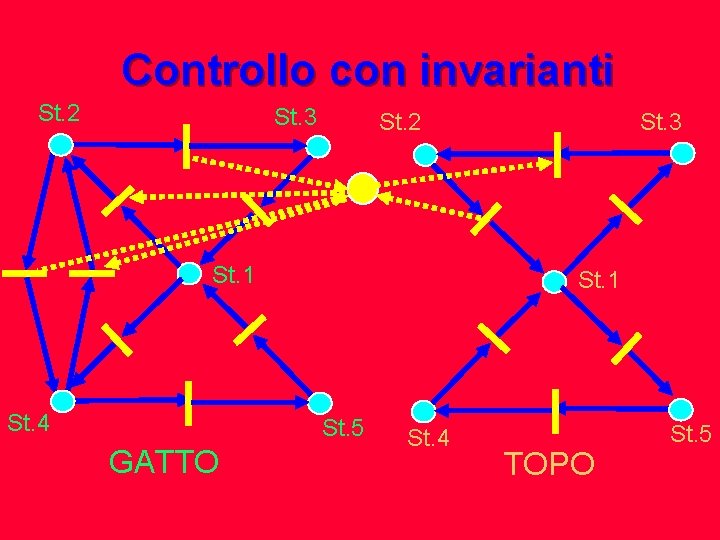
Controllo con invarianti SPECIFICHE PER IL PROCESSO: L c Mp B con Lc e B assegnati Cp : matr. inc. del processo Cc : matr. inc. del controllo Lc : matrice delle specifiche Cc : = - Lc Cp => Mp 0 : stato iniziale del processo Mc 0 : stato iniziale del controllo B : limiti specificati le righe di [ Lc Ic ] annullano la matrice di incidenza a ciclo chiuso Cp Cc sono cioè degli invarianti del sistema processo-controllo, ovvero: Lc. Mp 0 + Mc 0 = Lc. Mp + Mc Quindi se Mc 0 : = B - Lc. Mp 0 L c Mp = B - Mc B B = Lc. Mp + Mc

Controllo con invarianti St. 2 St. 3 St. 1 St. 4 St. 1 St. 5 GATTO St. 3 St. 2 St. 4 TOPO St. 5

Controllo con invarianti St. 2 St. 3 St. 1 St. 4 St. 1 St. 5 GATTO St. 3 St. 2 St. 4 TOPO St. 5

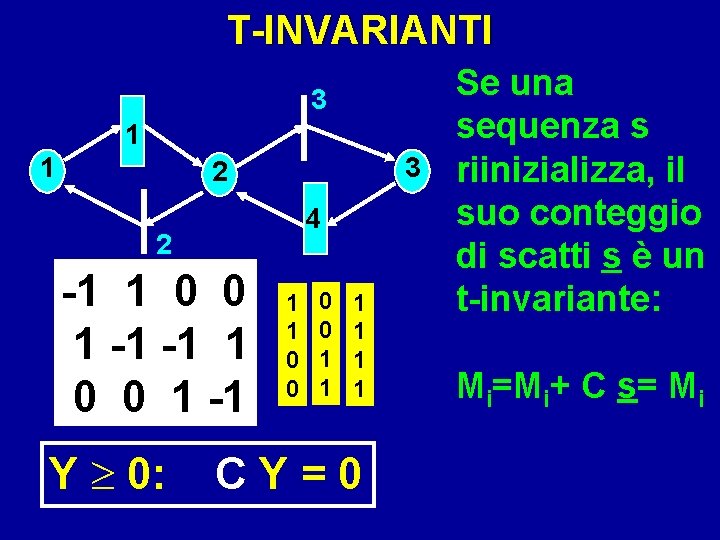
T-INVARIANTI 3 1 1 3 2 4 2 -1 1 0 0 1 -1 Y 0: 1 1 0 0 1 1 1 CY=0 Se una sequenza s riinizializza, il suo conteggio di scatti s è un t-invariante: Mi=Mi+ C s= Mi

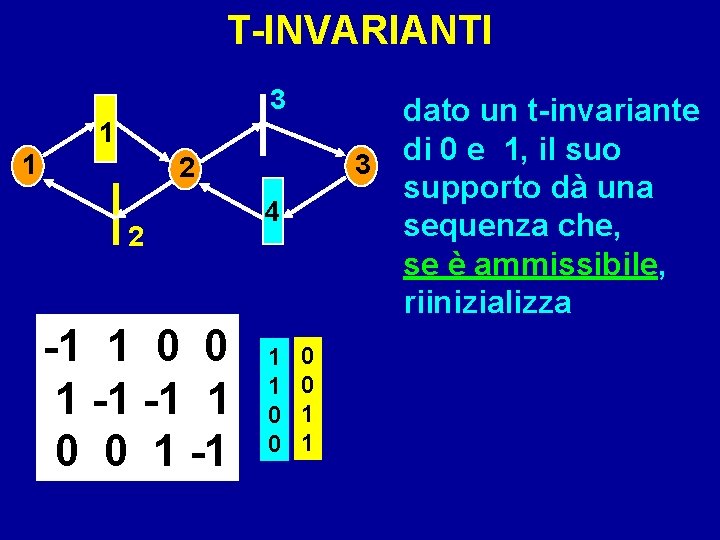
T-INVARIANTI 3 1 1 3 2 2 -1 1 0 0 1 -1 4 1 1 0 0 1 1 dato un t-invariante di 0 e 1, il suo supporto dà una sequenza che, se è ammissibile, riinizializza

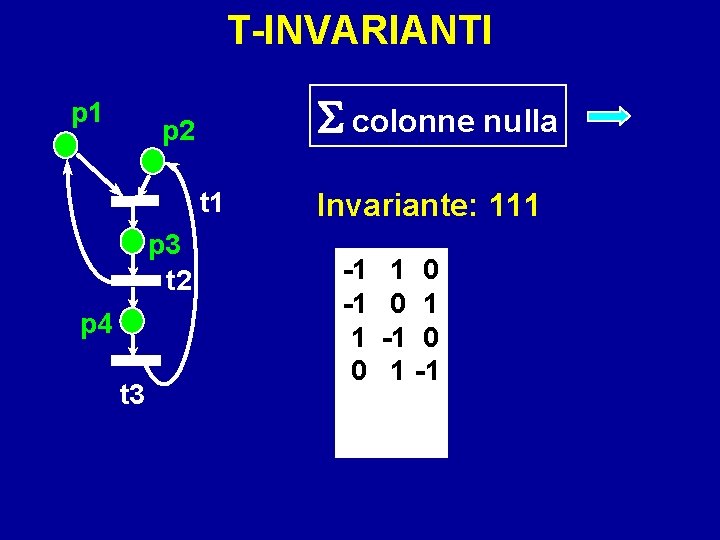
T-INVARIANTI p 1 colonne nulla p 2 t 1 p 3 t 2 p 4 t 3 Invariante: 111 -1 -1 1 0 1 0 -1

MACCHINE SMT Archetti, Sciomachen: RAPPRESENTAZIONE ED ANALISI, CON RETI DI PETRI, DI SISTEMI DI LAVORAZIONE - 1989 Consorzio Autofaber, Milano Magazzino componenti Magazzino utensili NORD testa nord braccio testa sud scheda SUD

- modulo B (“tool change & pick”): in cui una testa cambia attrezzo e preleva, mentre l’altra resta ferma - modulo C (“pick & place”): in cui le operazioni di fissaggio e di prelievo di un componente sono svolte concorrentemente dalle due teste

- modulo D (“pick”): in cui viene affettuato un prelievo di un componente da una delle due teste, mentre l’altra è ferma - modulo E (“place”): in cui viene affettuato solamente un fissaggio di un componente da una delle due teste, mentre l’altra è ferma

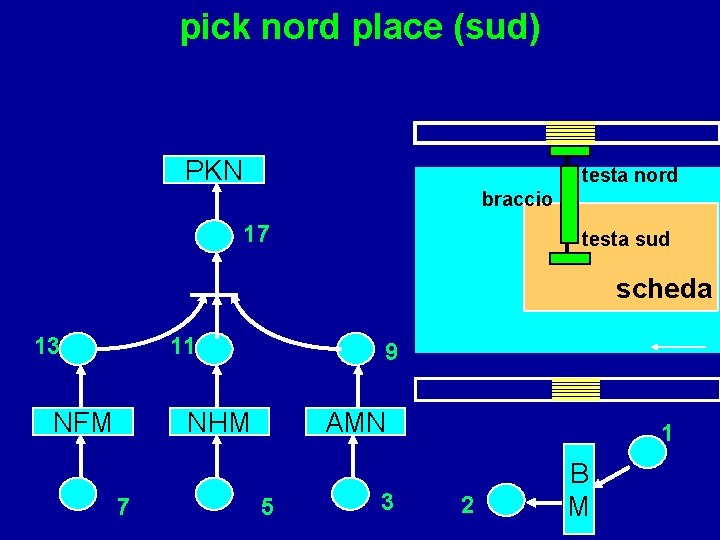
pick nord place sud testa nord braccio testa sud NFM NHM 7 AMN 5 s 1 3 B M

pick nord place (sud) PKN testa nord braccio 17 testa sud scheda 13 11 NFM 9 NHM 7 AMN 5 3 1 2 B M

BM: movimenti della scheda AMN: movimenti del braccio da sud a nord NFM: movimenti del magazzino nord NHM: movimenti di allineamento della testa nord per prelievo

AMS: movimenti del braccio da nord a sud SFM: movimenti del magazzino sud SHM: movimenti di allineamento della testa sud per prelievo

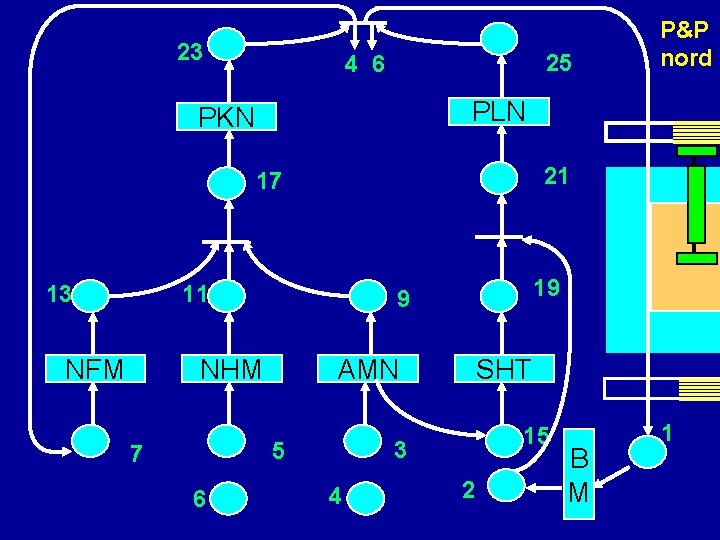
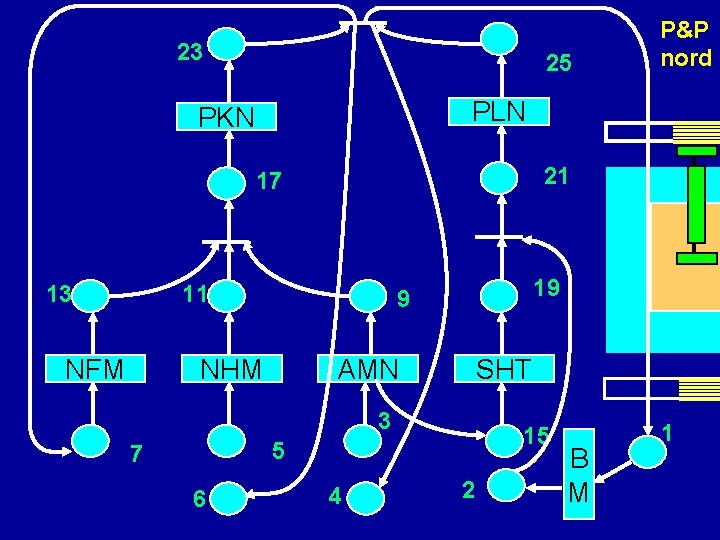
23 25 4 6 PLN PKN 21 17 13 11 NFM AMN SHT 15 3 5 6 19 9 NHM 7 P&P nord 4 2 B M 1

NHT: attività di preparazione della testa nord per fissaggio SHT: attività di preparazione della testa sud per fissaggio

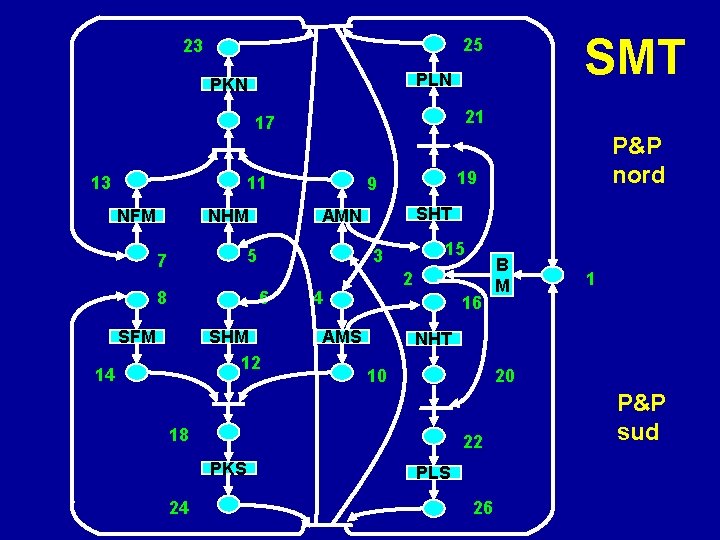
PLN PKN 21 17 13 11 NHM NFM 8 SFM 15 3 SHM 12 14 SHT AMN 6 2 4 16 AMS 24 B M 1 NHT 10 20 18 22 PKS P&P nord 19 9 5 7 SMT 25 23 PLS 26 P&P sud

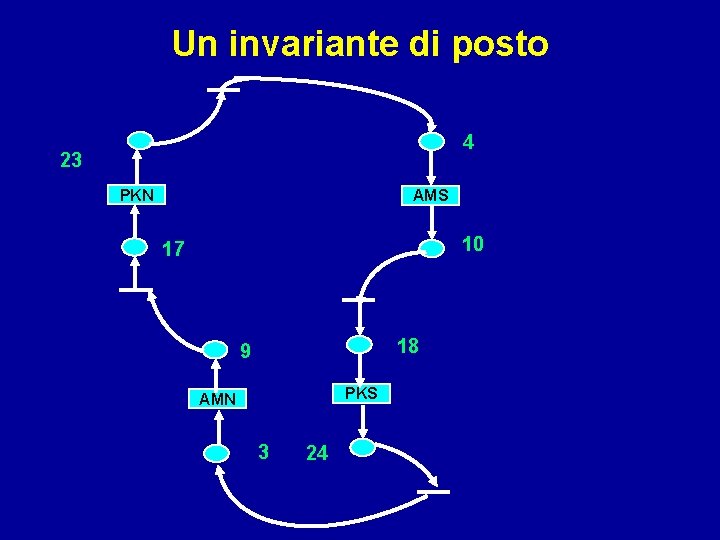
Un invariante di posto 4 23 PKN AMS 10 17 18 9 PKS AMN 3 24

Tutta la rete P&P è il supporto di un invariante di transizione minimale: YT = 2 1 1 1 1 1 Infatti la transizione BM deve scattare due volte e le altre 18 una sola per tornare alla condizione iniziale

23 25 PLN PKN 21 17 13 11 NFM 19 9 NHM AMN SHT 3 15 5 7 6 P&P nord 4 2 B M 1

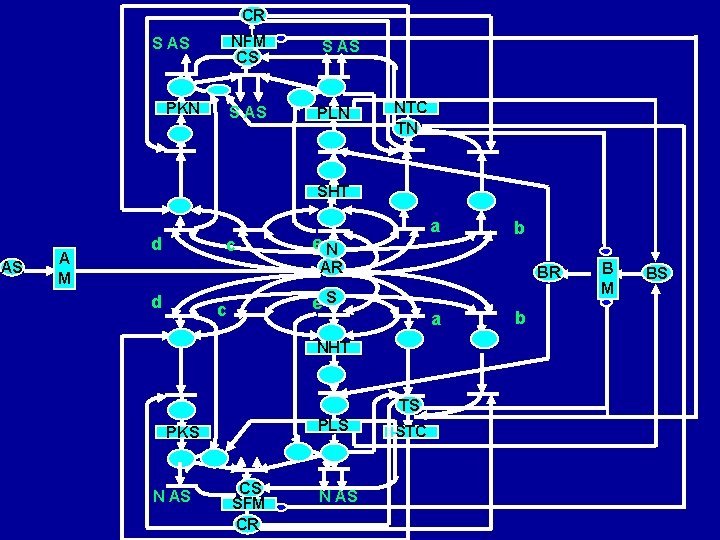
CR NFM S AS CS S AS PKN NTC PLN TN SHT d AS A M N c AR e a b BR B M BS

CR NFM CS S AS PKN S AS PLN NTC TN SHT AS A M d c a e. N b AR d BR e. S c a NHT TS PLS PKS N AS CS SFM CR N AS STC b B M BS