Esercizi e complementi di Economia dei Sistemi Industriali

Esercizi e complementi di Economia dei Sistemi Industriali 2 (teoria degli oligopoli) Introduzione alla Teoria dei Giochi Parte prima 1

TEORIA dei GIOCHI Oggetto di studio Le scelte di agenti razionali in un contesto di interazione strategica Contesto di scelta Un contesto di scelta è detto strategico quando le conseguenze di un’azione per un agente dipendono: v non soltanto dalle azioni da lui compiute v ma anche dalle azioni compiute da altri agenti 2

Il termine gioco è utilizzato per definire un generico contesto strategico Gioco cooperativo Gioco non cooperativo I giocatori possono comunicare e stabilire accordi vincolanti prima di iniziare a giocare I giocatori non possono comunicare e stabilire accordi vincolanti prima di iniziare a giocare Le imprese prima di competere sul mercato stabiliscono accordi vincolanti I giocatori scelgono le proprie strategie indipendentemente (non agiscono in modo concertato) 3

CLASSIFICAZIONI v GIOCHI STATICI I giocatori scelgono contemporaneamente v GIOCHI DINAMICI I giocatori effettuano la loro scelta secondo una sequenza prestabilita di mosse DESCRIZIONE DI UN GIOCO NON COOPERATIVO v FORMA NORMALE o STRATEGICA v FORMA ESTESA 4

DESCRIZIONE IN FORMA NORMALE G(N, S, u) La descrizione in forma normale è caratterizzata da 3 elementi: 1. Un insieme di giocatori N = {1, 2, . . , n} 2. Un insieme di strategie pure (spazio delle strategie pure) Si a disposizione di ciascun giocatore i N si Si indica una generica strategia pura S = S 1 S 2 … Sn indica l’insieme di tutte le possibili combinazioni di strategie pure s = (s 1 , s 2 , … , sn ) S indica una generica combinazione di strategie pure • Una funzione di payoff ui : S R per ciascun giocatore i N ui (s) è il payoff del giocatore i se i giocatori scelgono la combinazione di strategie s = (s 1 , s 2 , … , sn ) 5

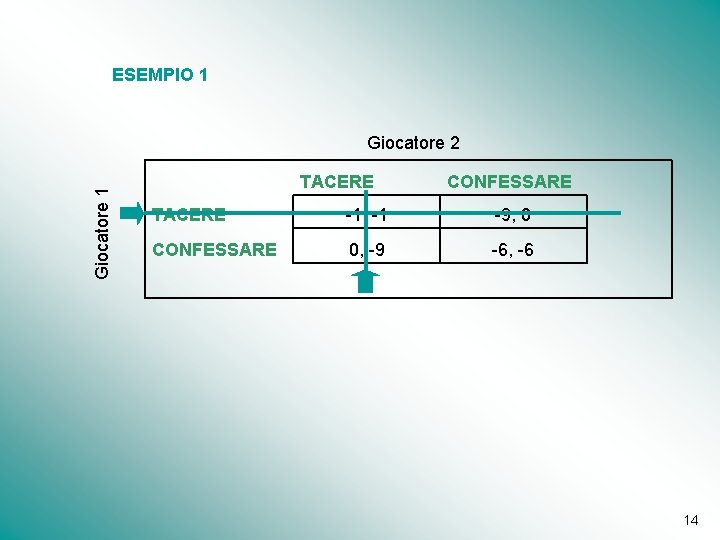
DILEMMA DEL PRIGIONIERO TACERE CONFESSARE TACERE -1, -1 -9, 0 CONFESSARE 0, -9 -6 , -6 Numero dei giocatori Insieme di strategie pure (spazio delle strategie pure) a disposizione di entrambi i giocatori 6

PAYOFF DEI GIOCATORI 7

DUOPOLIO DI COURNOT E BERTRAND 8

Dilemma del Prigioniero Modelli di Cournot e Bertrand GIOCHI STATICI CON INFORMAZIONE COMPLETA I giocatori scelgono le loro strategie “simultaneamente" (è sufficiente che ciascun giocatore scelga la propria strategia senza conoscere la scelta dell'altro) IMPORTANZA DELLA STRUTTURA INFORMATIVA DEL GIOCO Un gioco G è caratterizzato da informazione completa se tutti i giocatori informazione completa conoscono gli elementi che caratterizzano il gioco. N = {1, 2, . . , n} S = S 1 S 2 … Sn ui : S R i N 9

Informazione Completa Nel Dilemma Del Prigioniero Entrambi i giocatori conoscono la (bi)matrice del gioco TACERE CONFESSARE TACERE -1, -1 -9, 0 CONFESSARE 0, -9 -6 , -6 PREDIZIONE SULL'ESITO DEL GIOCO Procedura risolutiva: eliminazione iterata di strategie strettamente dominate 10

NOTAZIONI 11

DEFINIZIONI 12

LA PROCEDURA La procedura della eliminazione iterata di strategie strettamente dominate è basata sulla considerazione che giocatori razionali non scelgono strategie strettamente dominate nessuna credenza da parte di un giocatore, e relativa alle scelte degli avversari, è tale da rendere una strategia dominata una scelta ottima 13

ESEMPIO 1 Giocatore 2 TACERE CONFESSARE TACERE -1, -1 -9, 0 CONFESSARE 0, -9 -6, -6 14

ESEMPIO 2 Giocatore 1 SINISTRA CENTRO DESTRA SU 1, 0 1, 2 0, 1 GIU’ 0, 3 0, 1 2, 0 15

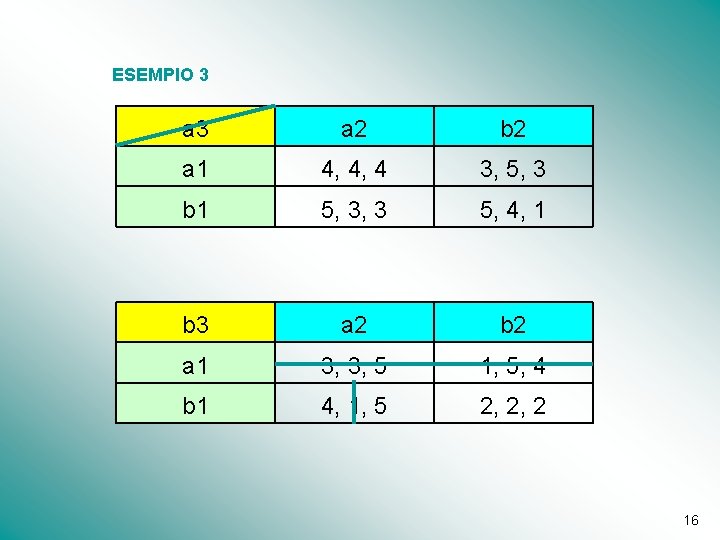
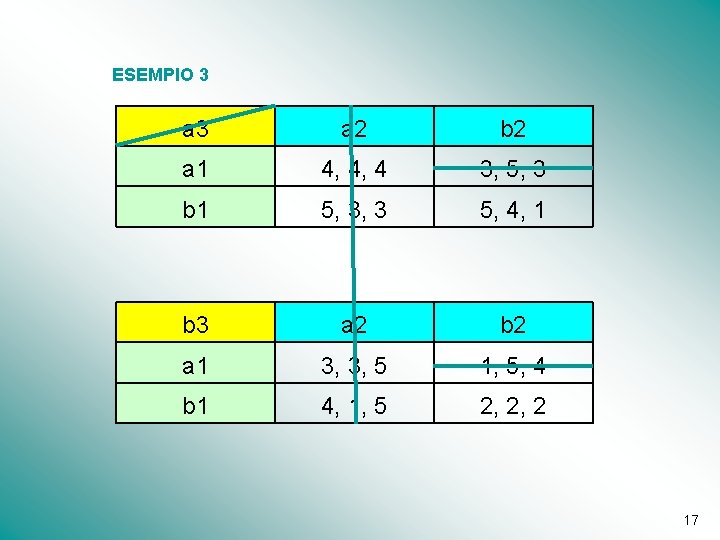
ESEMPIO 3 a 2 b 2 a 1 4, 4, 4 3, 5, 3 b 1 5, 3, 3 5, 4, 1 b 3 a 2 b 2 a 1 3, 3, 5 1, 5, 4 b 1 4, 1, 5 2, 2, 2 16

ESEMPIO 3 a 2 b 2 a 1 4, 4, 4 3, 5, 3 b 1 5, 3, 3 5, 4, 1 b 3 a 2 b 2 a 1 3, 3, 5 1, 5, 4 b 1 4, 1, 5 2, 2, 2 17

RAZIONALITA’ DEI GIOCATORI La procedura della eliminazione iterata di strategie strettamente dominate è basata sulla considerazione che: giocatori "razionali" non scelgono strategie strettamente dominate. "razionali" Nessuna credenza da parte di un giocatore, relativa alle scelte degli credenza avversari, è tale da rendere una strategia dominata una scelta ottima. L'applicazione del procedimento per un numero arbitrario di passi richiede la seguente assunzione: la "razionalità" dei giocatori è conoscenza comune (common knowledge) knowledge vtutti i giocatori sono razionali; vtutti i giocatori sanno che tutti sono razionali, ecc. . 18

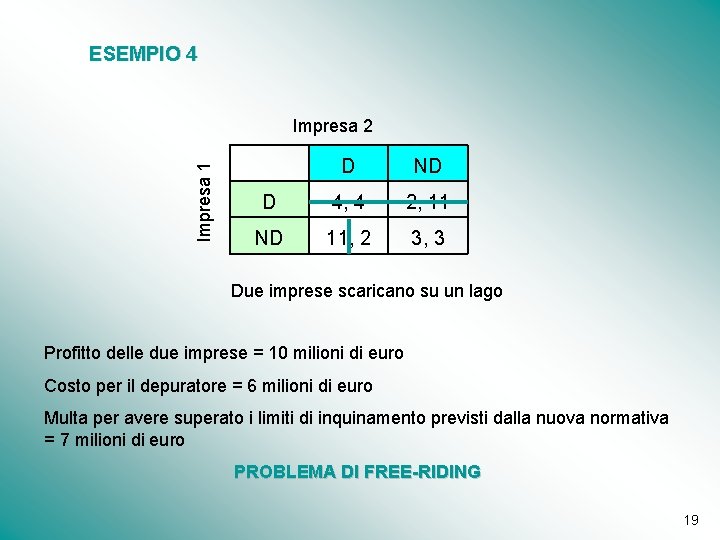
ESEMPIO 4 Impresa 1 Impresa 2 D ND D 4, 4 2, 11 ND 11, 2 3, 3 Due imprese scaricano su un lago Profitto delle due imprese = 10 milioni di euro Costo per il depuratore = 6 milioni di euro Multa per avere superato i limiti di inquinamento previsti dalla nuova normativa = 7 milioni di euro PROBLEMA DI FREE-RIDING 19

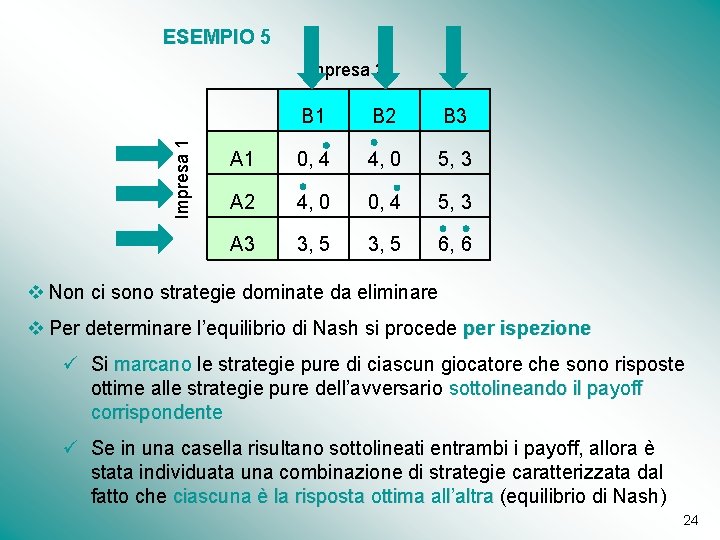
ESEMPIO 5 Impresa 1 Impresa 2 B 1 B 2 B 3 A 1 0, 4 4, 0 5, 3 A 2 4, 0 0, 4 5, 3 A 3 3, 5 6, 6 v non ci sono strategie dominate da eliminare v In questo caso l’eliminazione delle strategie strettamente dominate non risolve il gioco, in generale non risolve tutte le classi di problemi v Ci serve un criterio di soluzione più forte v Il criterio con maggiore forza di predizione è l’equilibrio di Nash 20

EQUILIBRIO DI NASH Una combinazione di strategie è un equilibrio di Nash se per ogni giocatore i e per ogni strategia ammissibile un equilibrio di Nash richiede che la strategia di ogni giocatore i sia ottimale rispetto alle strategie ottimali degli avversari 21

EQUILIBRIO DI NASH risolve il problema: Ø Per ogni giocatore i la strategia si* e la migliore risposta del giocatore i alle strategie prescritte per gli altri n-1 giocatori Ø Nessun giocatore, preso singolarmente, desidera deviare dalla strategia prescritta Ø L'equilibrio di Nash è una predizione sull'esito del gioco strategicamente stabile o autovincolante (self-enforcing) 22

EQUILIBRIO DI NASH Se l'eliminazione iterata di strategie strettamente dominate rimuove tutte le strategie tranne s'= (s’i, s’-i), allora queste strategie sono l'unico equilibrio di Nash Le strategie corrispondenti ad un equilibrio di Nash sopravvivono alla eliminazione iterata di strategie strettamente dominate, ma non e vero il contrario Non è detto che una strategia che sopravvive alla eliminazione iterata di strategie strettamente dominate faccia parte di un equilibrio di Nash 23

ESEMPIO 5 Impresa 1 Impresa 2 B 1 B 2 B 3 A 1 0, 4 4, 0 5, 3 A 2 4, 0 0, 4 5, 3 A 3 3, 5 6, 6 v Non ci sono strategie dominate da eliminare v Per determinare l’equilibrio di Nash si procede per ispezione ü Si marcano le strategie pure di ciascun giocatore che sono risposte marcano ottime alle strategie pure dell’avversario sottolineando il payoff corrispondente ü Se in una casella risultano sottolineati entrambi i payoff, allora è stata individuata una combinazione di strategie caratterizzata dal fatto che ciascuna è la risposta ottima all’altra (equilibrio di Nash) ciascuna è la risposta ottima all’altra 24

OSSERVAZIONE tutte le strategie sopravvivono alla eliminazione iterata di strategie strettamente dominate, ma solo la combinazione (A 3, B 3) soddisfa le seguenti condizioni: PROPOSIZIONE Se l'eliminazione iterata di strategie strettamente dominate rimuove tutte le strategie tranne , allora queste strategie sono l'unico equilibrio di Nash 25

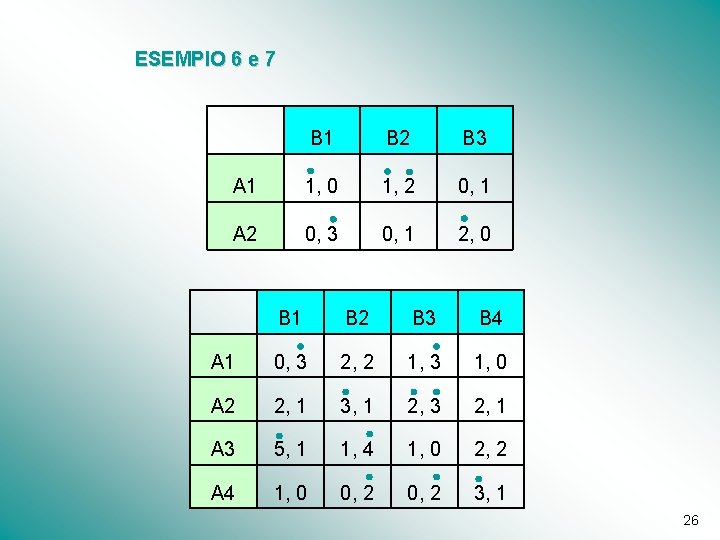
ESEMPIO 6 e 7 B 1 B 2 B 3 A 1 1, 0 1, 2 0, 1 A 2 0, 3 0, 1 2, 0 B 1 B 2 B 3 B 4 A 1 0, 3 2, 2 1, 3 1, 0 A 2 2, 1 3, 1 2, 3 2, 1 A 3 5, 1 1, 4 1, 0 2, 2 A 4 1, 0 0, 2 3, 1 26

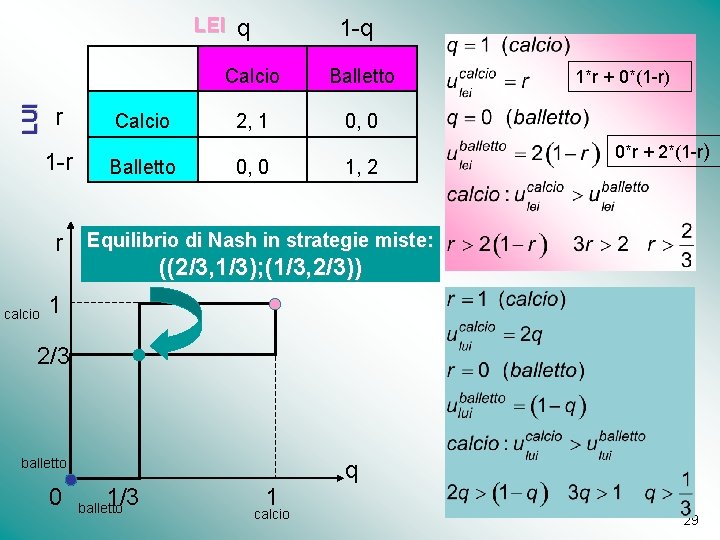
ESEMPIO 8 (BATTAGLIA DEI SESSI) Entrambi i giocatori desiderano trascorrere la serata insieme piuttosto che da soli, tuttavia “Iui" preferisce la partita mentre “Iei" preferisce il balletto Ciascun giocatore consegue: ü un payoff pari a 2 se entrambi vanno allo spettacolo da lui/lei preferito ü un payoff pari a 1 se entrambi vanno allo spettacolo preferito dall'altro ü un payoff pari a 0 se ognuno trascorre la serata da solo LUI LEI Partita Balletto Partita 2, 1 0, 0 Balletto 0, 0 1, 2 27

ESISTENZA DELL'EQUILIBRIO DI NASH Teorema. (Nash, 1950) Teorema Ogni gioco finito ammette almeno un equilibrio di Nash (eventualmente in strategie miste) Definizione: Un gioco è finito se il numero dei giocatori e quello Definizione: delle strategie pure è finito. Altrimenti è infinito. Definizione: 28

LUI LEI r 1 -r q 1 -q Calcio Balletto Calcio 2, 1 0, 0 Balletto 0, 0 1, 2 1*r + 0*(1 -r) 0*r + 2*(1 -r) r Equilibrio di Nash in strategie miste: ((2/3, 1/3); (1/3, 2/3)) calcio 1 2/3 balletto 0 1/3 balletto 1 calcio q 29

MATCHING PENNIES q 1 -q TESTA CROCE r TESTA -1, 1 1, -1 1 -r CROCE 1, -1 -1, 1 r Equilibrio di Nash in strategie miste: ((1/2, 1/2); (1/2, 1/2)) testa 1 1/2 q croce 0 croce 1/2 1 testa 30

Teorema (Glicksberg, Debreu; 1952) Un gioco per il quale valgano le seguenti ipotesi: • il numero dei giocatori è finito • Si è un sottoinsieme compatto e convesso di uno spazio euclideo per ogni giocatore i N • ui é una funzione continua in s S per ogni i N ammette almeno un equilibrio di Nash. Se inoltre ui é una funzione quasi-concava in si per ogni i N, allora ammette almeno un equilibrio di Nash in strategie pure. 31