ESE 535 Electronic Design Automation Day 23 April

ESE 535: Electronic Design Automation Day 23: April 22, 2009 Statistical Static Timing Analysis 1 Penn ESE 535 Spring 2009 -- De. Hon

Today • • Sources of Variation Limits of Worst Case Optimization for Parametric Yield Statistical Analysis 2 Penn ESE 535 Spring 2009 -- De. Hon

Central Problem Mean Number of Dopant Atoms • As our devices approach the atomic scale, we must deal with statistical effects governing the placement and behavior of individual atoms and electrons. 10000 100 10 1000 500 250 130 65 32 Technology Node (nm) Penn ESE 535 Spring 2009 -- De. Hon 16 • Transistor critical dimensions • Atomic discreteness • Subwavelength litho • Etch/polish rates • Focus • Number of dopants 3 • Dopant Placement

Oxide Thickness [Asenov et al. TRED 2002] 4 Penn ESE 535 Spring 2009 -- De. Hon

Line Edge Roughness • 1. 2 m and 2. 4 m lines From: http: //www. microtechweb. com/2 d/lw_pict. htm 5 Penn ESE 535 Spring 2009 -- De. Hon

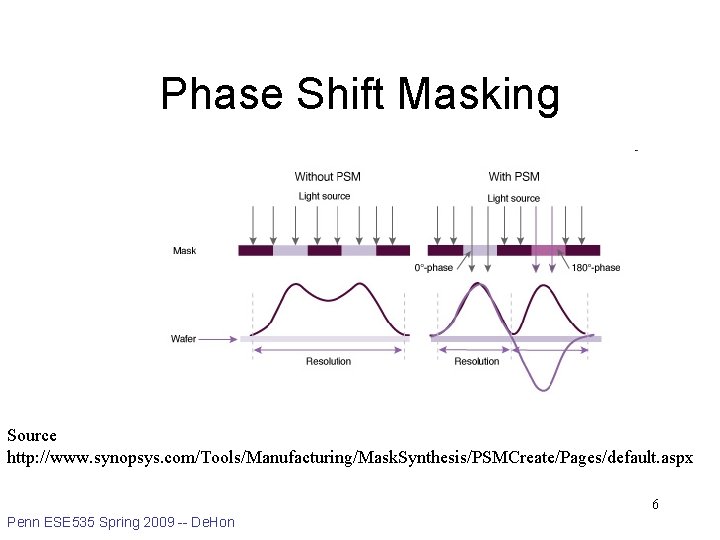
Phase Shift Masking Source http: //www. synopsys. com/Tools/Manufacturing/Mask. Synthesis/PSMCreate/Pages/default. aspx 6 Penn ESE 535 Spring 2009 -- De. Hon

Line Edges (PSM) Source: http: //www. solid-state. com/display_article/122066/5/none/Feat/Developments-in-materials-for-157 nm-photoresists 7 Penn ESE 535 Spring 2009 -- De. Hon

Intel 65 nm SRAM (PSM) Source: 8 http: //www. intel. com/technology/itj/2008/v 12 i 2/5 -design/figures/Figure_5_lg. gif Penn ESE 535 Spring 2009 -- De. Hon

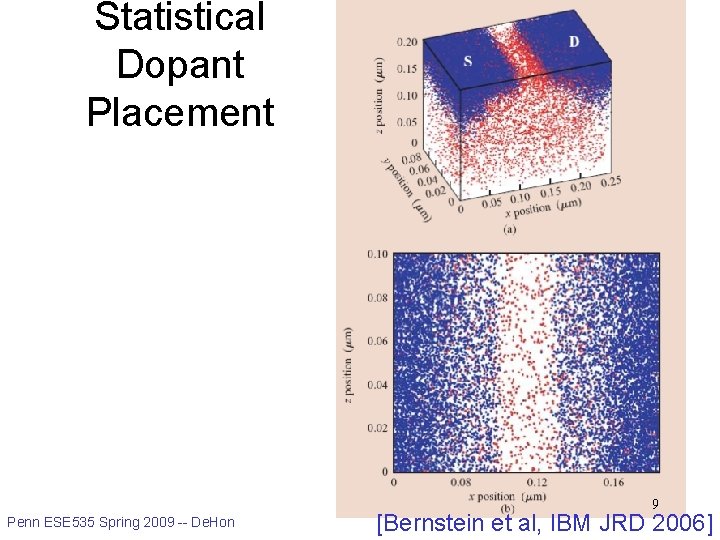
Statistical Dopant Placement 9 Penn ESE 535 Spring 2009 -- De. Hon [Bernstein et al, IBM JRD 2006]

Vth Variability @ 65 nm 10 Penn ESE 535 Spring 2009 -- De. Hon [Bernstein et al, IBM JRD 2006]

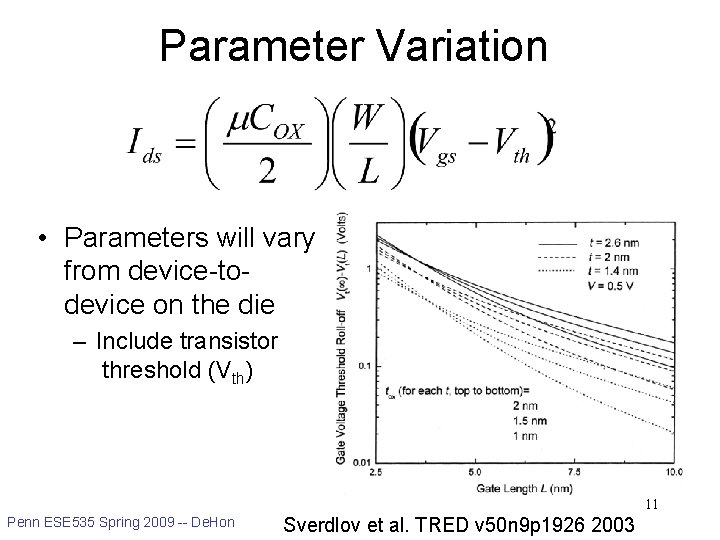
Parameter Variation • Parameters will vary from device-todevice on the die – Include transistor threshold (Vth) 11 Penn ESE 535 Spring 2009 -- De. Hon Sverdlov et al. TRED v 50 n 9 p 1926 2003

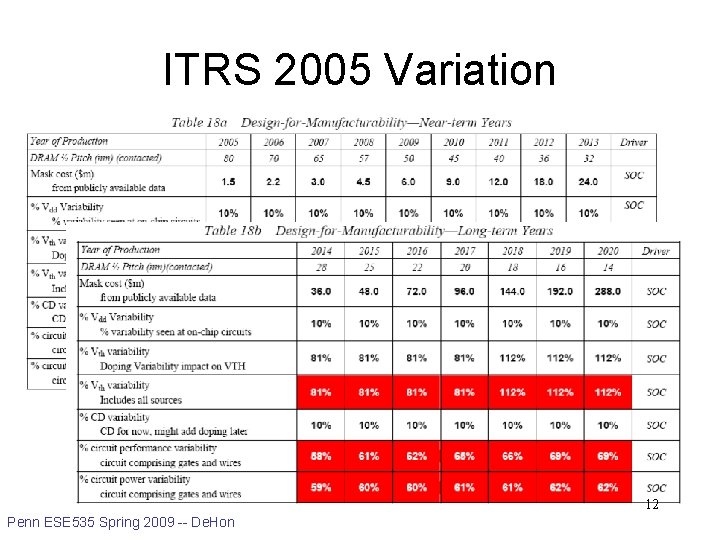
ITRS 2005 Variation 12 Penn ESE 535 Spring 2009 -- De. Hon

Source: Noel Menezes, Intel ISPD 2007 13 Penn ESE 535 Spring 2009 -- De. Hon

Source: Noel Menezes, Intel ISPD 2007 14 Penn ESE 535 Spring 2009 -- De. Hon

Old Way • Characterize gates by corner cases – Fast, nominal, slow • Add up corners to estimate range 15 Penn ESE 535 Spring 2009 -- De. Hon

Corners Misleading Penn ESE 535 Spring 2009 -- De. Hon [Orshansky+Keutzer DAC 2002] 16

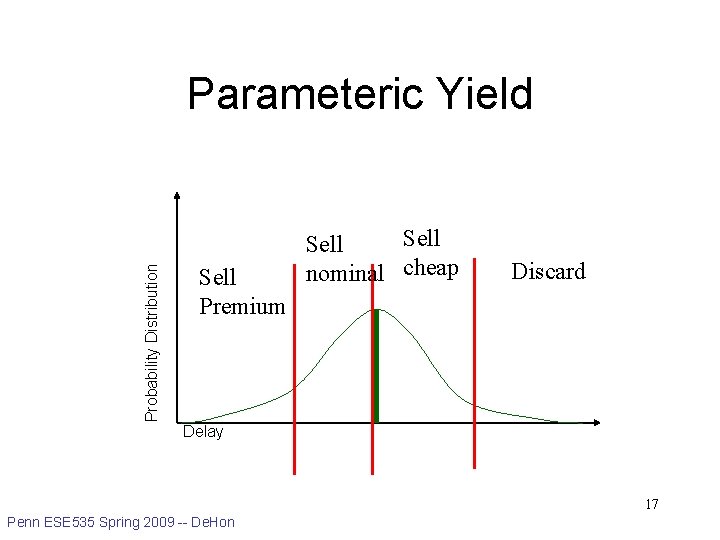
Probability Distribution Parameteric Yield Sell Premium Sell nominal cheap Discard Delay 17 Penn ESE 535 Spring 2009 -- De. Hon

Phenomena 1: Path Averaging • Tpath = t 0+t 1+t 2+t 3+…t(d-1) • Ti – iid random variables – Mean t – Variance • Tpath – Mean d×t – Variance = d × 18 Penn ESE 535 Spring 2009 -- De. Hon

Sequential Paths • Tpath = t 0+t 1+t 2+t 3+…t(d-1) • Tpath – Mean d×t – Variance = d × • 3 sigma delay on path: d×t + 3 d × – Worst case per component would be: d×(t+3 ) – Overestimate d vs. d 19 Penn ESE 535 Spring 2009 -- De. Hon

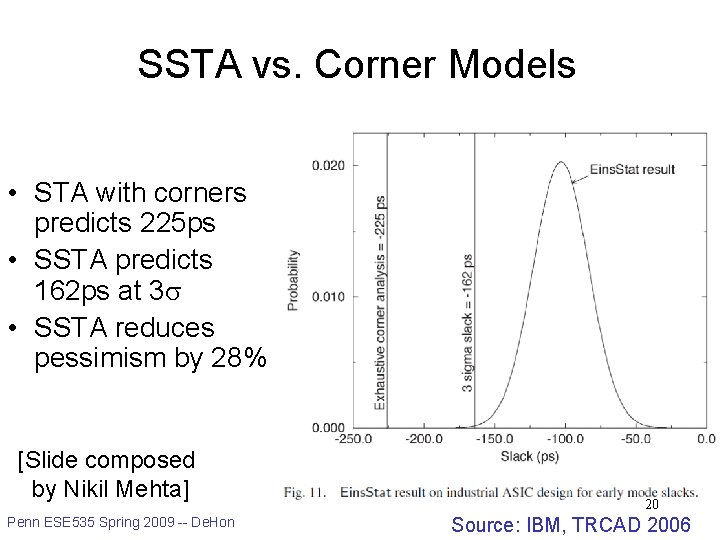
SSTA vs. Corner Models • STA with corners predicts 225 ps • SSTA predicts 162 ps at 3 • SSTA reduces pessimism by 28% [Slide composed by Nikil Mehta] Penn ESE 535 Spring 2009 -- De. Hon 20 Source: IBM, TRCAD 2006

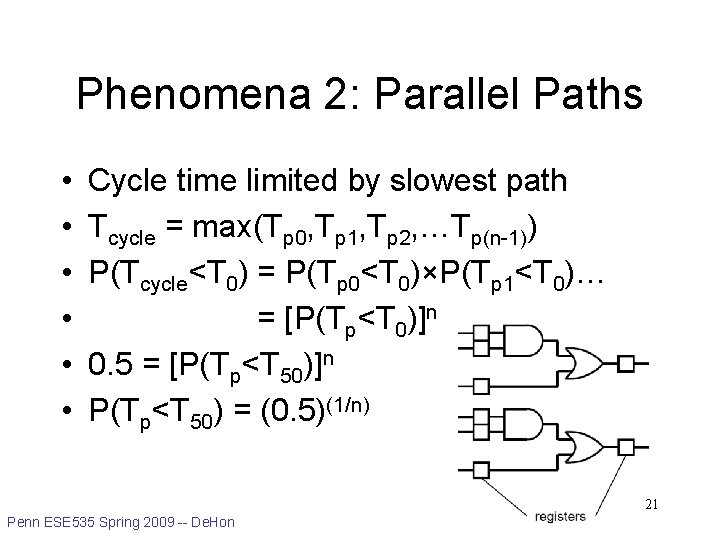
Phenomena 2: Parallel Paths • • • Cycle time limited by slowest path Tcycle = max(Tp 0, Tp 1, Tp 2, …Tp(n-1)) P(Tcycle<T 0) = P(Tp 0<T 0)×P(Tp 1<T 0)… = [P(Tp<T 0)]n 0. 5 = [P(Tp<T 50)]n P(Tp<T 50) = (0. 5)(1/n) 21 Penn ESE 535 Spring 2009 -- De. Hon

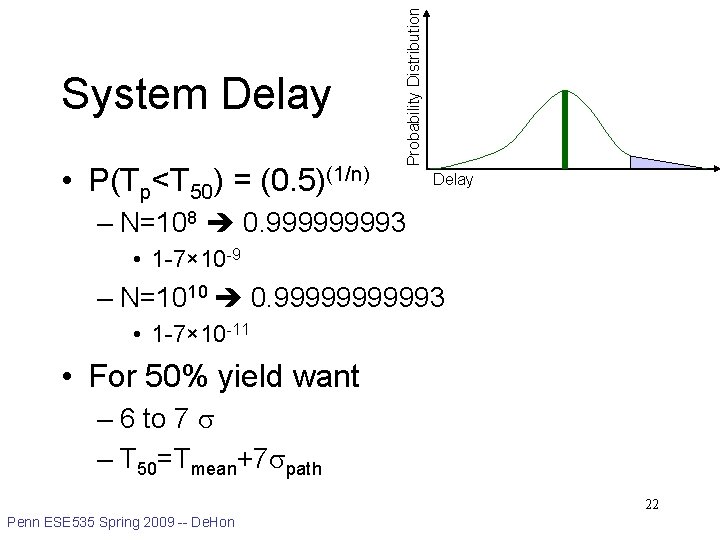
• P(Tp<T 50) = (0. 5)(1/n) Probability Distribution System Delay – N=108 0. 99993 • 1 -7× 10 -9 – N=1010 0. 999993 • 1 -7× 10 -11 • For 50% yield want – 6 to 7 – T 50=Tmean+7 path 22 Penn ESE 535 Spring 2009 -- De. Hon

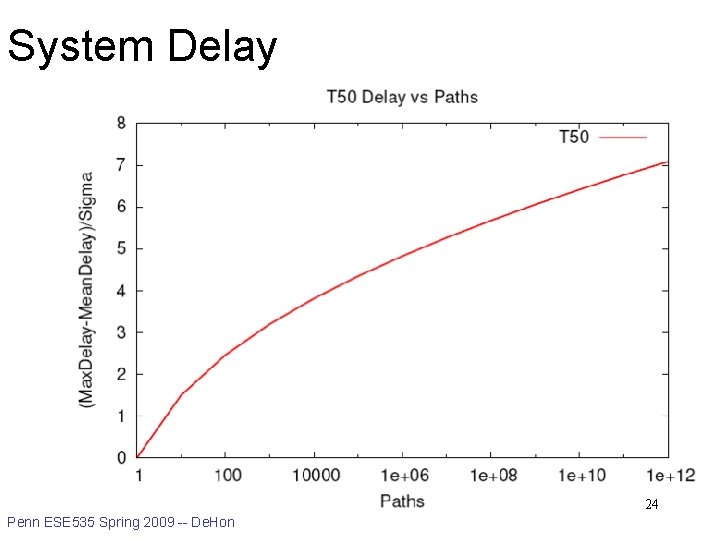
System Delay 23 Penn ESE 535 Spring 2009 -- De. Hon

System Delay 24 Penn ESE 535 Spring 2009 -- De. Hon

Corners Misleading Phenomena 2 Phenomena 1 Penn ESE 535 Spring 2009 -- De. Hon [Orshansky+Keutzer DAC 2002] 25

Source: Noel Menezes, Intel ISPD 2007 26 Penn ESE 535 Spring 2009 -- De. Hon

But does worst-case mislead? • STA with worst-case says these are equivalent: 27 Penn ESE 535 Spring 2009 -- De. Hon

What do we need to do? • Ideal: – Compute PDF for delay at each gate – Compute delay of a gate as a PDF from: • PDF of inputs • PDF of gate delay 28 Penn ESE 535 Spring 2009 -- De. Hon

Delay Calculation Day 15 AND rules 29 Penn ESE 535 Spring 2009 -- De. Hon

What do we need to do? • Ideal: – compute PDF for delay at each gate – Compute delay of a gate as a PDF from: • PDF of inputs • PDF of gate delay – Need to compute for distributions • SUM • MAX (maybe min) 30 Penn ESE 535 Spring 2009 -- De. Hon

Dealing with PDFs • Simple model assume all PDFs are Gaussian – Model with mean, – Imperfect • Not all phenomena are Gaussian • Sum of Gaussians is Gaussian • Max of Gaussians is not a Gaussian 31 Penn ESE 535 Spring 2009 -- De. Hon

Sum of Gaussians • Two Guassians – A, A and B, B – SUM = (A+B), – If identical • SUM = 2 A, A 2 32 Penn ESE 535 Spring 2009 -- De. Hon

Tightness Probability (toward max) Gaussian PDF with zero mean and unit variance Prob(X<y) Standard deviation of SUM(A, B) (if A & B uncorrelated) Prob(X<(Anom – Bnom)/ A+B)) Penn ESE 535 Spring 2009 -- De. Hon [Source: Nikil Mehta] 33

MAX of Two Gaussians • Expected value – Weighted sum of means – Additional term which adds fraction of SUM(A, B) • Variance – Weighted sum of variance – Some other terms? Penn ESE 535 Spring 2009 -- De. Hon [Source: Nikil Mehta] 34

MAX of Two Identical Gaussians • Given two identical Gaussians A and B with and • Plug into equations • E[MAX(A, B)] = + /( )1/2 • VAR[MAX(A, B)] = 2 – / [Source: Nikil Mehta] 35 Penn ESE 535 Spring 2009 -- De. Hon

[Source: Nikil Mehta] STA Example • Example circuit – Each component has a delay – Nets are numbered 3 1 2 2 3 4 4 1 6 3 6 5 12 5 3 2 7 36 Penn ESE 535 Spring 2009 -- De. Hon

[Source: Nikil Mehta] STA Example • Transform into a timing graph – Nodes = nets – Edges = gates (many edges can correspond to the same gate) 3 1 2 2 4 3 1 4 6 3 6 12 0 6 5 12 Penn ESE 535 Spring 2009 -- De. Hon S 3 2 7 0 37

[Source: Nikil Mehta] STA Example • Goal is to compute arrival time on output t=0 3 1 t=0 2 2 t=0 4 3 t=0 1 4 6 3 6 12 0 6 5 12 Penn ESE 535 Spring 2009 -- De. Hon S 3 2 7 0 38

[Source: Nikil Mehta] STA Example 3 1 t=3 2 2 12 t=14 4 12 3 t=16 t=4 12 1 t=13 4 t=1 2009 -- De. Hon Penn ESE 535 Spring 6 3 6 t=9 0 6 5 5 S 3 2 7 0 39

[Source: Nikil Mehta] STA Example – For nodes with multiple inputs • Arrival time = MAX(input arrival times) 3 1 t=3 2 2 12 t=14 4 12 3 t=16 t=4 12 1 t=13 4 t=1 2009 -- De. Hon Penn ESE 535 Spring 6 3 6 t=9 0 6 5 5 t=21 S 3 2 7 0 40

[Source: Nikil Mehta] STA Example 3 1 t=3 2 2 12 t=14 4 12 3 t=16 t=4 12 1 t=13 4 t=1 2009 -- De. Hon Penn ESE 535 Spring 6 3 6 t=9 0 6 5 t=27 5 t=21 S 3 t=24 2 7 0 41

[Source: Nikil Mehta] STA Example 3 1 t=3 2 2 12 t=14 4 12 3 t=16 t=4 12 1 t=13 4 t=1 2009 -- De. Hon Penn ESE 535 Spring 6 3 6 t=9 6 5 t=30 0 t=30 t=27 5 t=21 3 t=24 2 7 t=26 0 t=26 S t=30 42

[Source: Nikil Mehta] SSTA Example • Represent delay and arrival time statistically ( , ) • Picking large variance (10) for all delays (3, 10) 1 t=(3, 10) (2, 10) 2 (12, 10) t=(2, 10) (4, 10) (12, 10) 3 t=(4, 10) (12, 10) 4 Penn ESE 535 t=(1, 10) Spring 2009 -- De. Hon (6, 10) (3, 10) 6 (6, 10) (0, 0) (5, 10) 5 (3, 10) (0, 0) S (2, 10) 7 43

[Source: Nikil Mehta] SSTA Example • Perform statistical SUM’s • Once we get to node 5, calculate tightness probabilities of input edges – Will allow us to perform statistical MAX – MAX is computed pairwise (3, 10) 1 (6, 10) (3, 10) t=(9, 14) 6 (2, 10) (6, 10) 2 (12, 10) t=(14, 14) 0. 35 (5, 10) (4, 10) (12, 10) 0. 43 3 5 t=(16, 14) t=(4, 10) 0. 22 t=(32, 14) (3, 10) (2, 10) (12, 10) t=(13, 14) 4 7 Penn ESE 535 t=(1, 10) Spring 2009 -- De. Hon (0, 0) S 44

[Source: Nikil Mehta] SSTA Example • Finish forward pass – Now, have statistical delay pdf of circuit – Normal distribution with =51 and =15 (3, 10) 1 t=(3, 10) (6, 10) 0. 03 (3, 10) t=(9, 14) 6 (6, 10) 0. 97 t=(44, 17) (2, 10) (0, 0) 2 (12, 10) t=(14, 14) 0. 64 0. 35 (5, 10) t=(44, 17) t=(38, 17) (4, 10) (12, 10) 0. 43 3 5 S t=(16, 14) (0, 0) t=(4, 10) t=(51, 15) 0. 22 t=(32, 14) (3, 10) 0. 36 (2, 10) (12, 10) t=(35, 17) t=(13, 14) t=(37, 20) 4 1. 00 7 45 t=(1, 10) Penn ESE 535 Spring 2009 -- De. Hon t=(37, 20)

[Source: Nikil Mehta] SSTA Example • Also have statistical criticality of all paths – Criticality ´ Product of tightness probabilities along path – SSTA outputs list of paths in order of criticality • On backward pass can calculate – Statistical slack – Statistical node/edge criticality 1 0. 03 6 2 0. 97 0. 35 3 0. 43 Printing critical paths (7/7) … [crit=0. 27](node 3 ->sink) [crit=0. 21](node 2 ->sink) [crit=0. 15](node 3 ->sink) [crit=0. 13](node 4 ->sink) [crit=0. 12](node 2 ->sink) [crit=0. 07](node 4 ->sink) [crit=0. 02](node 1 ->sink) 0. 64 5 S 0. 22 4 Penn ESE 535 Spring 2009 -- De. Hon 0. 36 1. 00 7 46

Probability of Path Being Critical [Source: Intel DAC 2005] 47 Penn ESE 535 Spring 2009 -- De. Hon

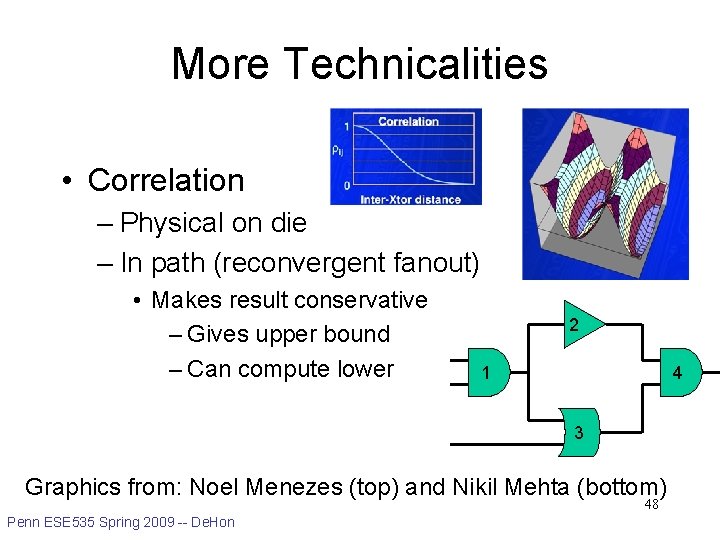
More Technicalities • Correlation – Physical on die – In path (reconvergent fanout) • Makes result conservative – Gives upper bound – Can compute lower 2 1 4 3 Graphics from: Noel Menezes (top) and Nikil Mehta (bottom) 48 Penn ESE 535 Spring 2009 -- De. Hon

SSTA vs. Monte Carlo Verification Time Source: IBM, TRCAD 2006 49 Penn ESE 535 Spring 2009 -- De. Hon

Using SSTA in FPGA CAD [Slide composed by Nikil Mehta] • Le Hei – FPGA 2007 – SSTA Synthesis, Place, Route • Kia – FPGA 2007 – Route with SSTA 50 Penn ESE 535 Spring 2009 -- De. Hon

Summary • Nanoscale fabrication is a statistical process • Delays are PDFs • Assuming each device is worst-case delay is too pessimistic – Wrong prediction about timing – Leads optimization in wrong direction • Reformulate timing analysis as statistical calculation • Estimate the PDF of circuit delays • Use this to drive optimizations 51 Penn ESE 535 Spring 2009 -- De. Hon

Admin • Reading for Monday online • Online Course Evaluations – http: //www. upenn. edu/eval 52 Penn ESE 535 Spring 2009 -- De. Hon

Big Ideas: • Coping with uncertainty • Statistical Reasoning and Calculation 53 Penn ESE 535 Spring 2009 -- De. Hon