ES 2501 StaticsUnit 15 1 Equilibrium of Rigid

ES 2501: Statics/Unit 15 -1: Equilibrium of Rigid Bodies: 3 D Problems Equilibrium Equations (3 D): Total Force is zero Total Moment about A is zero Scalar Form Ai z A y x Force eqns can be replaced by moment equation(s about other points, Say, Maximum six independent scalar equations to solve for six unknowns If # of unknowns > # of equilibrium equations Statically indeterminate problems

ES 2501: Statics/Unit 15 -2: Equilibrium of Rigid Bodies: 3 D Problems Basic Procedures of Static Analysis Step 1: Draw free-body diagram(s); Step 2: List equilibrium equations; Step 3: Any supplementary equations? (for statically indeterminate problems); Step 4: Solution; Step 5: Interpretation.

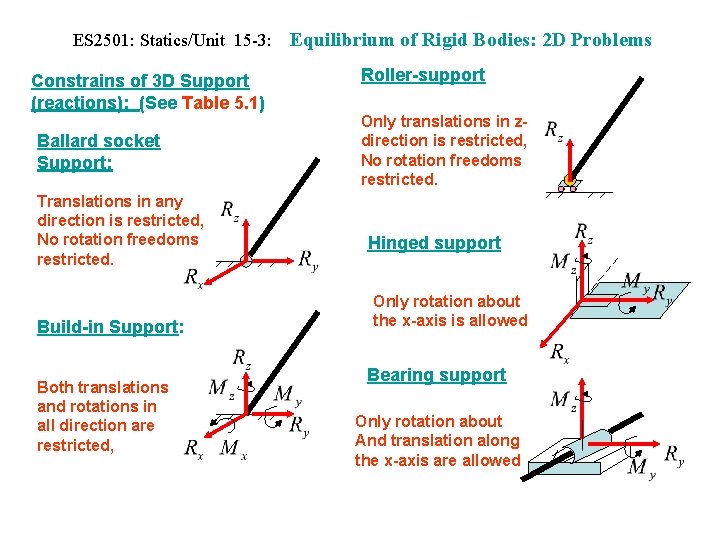
ES 2501: Statics/Unit 15 -3: Constrains of 3 D Support (reactions): (See Table 5. 1) Ballard socket Support: Translations in any direction is restricted, No rotation freedoms restricted. Build-in Support: Both translations and rotations in all direction are restricted, Equilibrium of Rigid Bodies: 2 D Problems Roller-support Only translations in zdirection is restricted, No rotation freedoms restricted. Hinged support Only rotation about the x-axis is allowed Bearing support Only rotation about And translation along the x-axis are allowed

ES 2501: Statics/Unit 15 -4: Example 1: E(0, 80, 100) A square plate with side of 200 mm is hinged at both A and B and supported by a cable to a hook E on the wall. The plate is held horizontally. A force of 400 N is applied at D downwards. Assume that hinge A doesn’t restrict motion in the hinge axis. y B(0, 0, 0) (Hinges are well aligned such that no extra couple on the plate) C(200, 0, 0) A(0, 0, 200) z Equilibrium of Rigid Bodies: 2 D Problems x Step 1: FBD (See the figure) Step 2: List Equilibrium equations. Zero total force D(200, 0, 200) Zero total moment about B Reaction at A Reaction at B Tension in cable CE (sign convention) Step 3: Solution 6 equations for 6 unknowns