Erzeugung und Verwendung von Zufallszahlen Modellierung von zuflligen

Erzeugung und Verwendung von Zufallszahlen • • Modellierung von zufälligen Prozessen Anforderungen an eine Zufallszahlengenerator Generierung einer exponentialverteilte Zufallszahl Empfehlungen zur Anwendungen der Zufallszahlenströme Bestimmung der Güte der Simulationsergebnisse durch Konfidenzintervalle Abhängigkeiten zwischen Simulationsergebnissen Literatur zur Simulation und Statistik

Modellierung von zufälligen Prozessen mittels Zufallszahlengeneratoren • Zufallszahlengeneratoren erzeugen eine Folge von Zahlen (Zufallszahlenstrom), die möglichst viele Eigenschaften von Zufallszahlen haben. • Da die Erzeugung von Zufallszahlen auf deterministischen Algorithmen beruht, ist die entstehende Zahlenfolge nicht wirklich zufällig. Deshalb wird oft von Pseudozufallszahlen gesprochen. In Computerprogrammen werden "Zufallszahlen" nach bestimmten Algorithmen berechnet, d. h. es sind gar keine echten Zufallszahlen, sondern "Pseudozufallszahlen". Von den so bestimmten Pseudozufallszahlen verlangt man eine möglichst gute Annäherung an "echte" Zufallszahlen, z. B. sollten die einzelnen Zahlen mit gleicher Häufigkeit auftreten, Wiederholungen von Zahlen sollten die gleiche Häufigkeit wie bei echten Zufallsziffern haben. • Die von dem Zufallszahlengenerator erzeugte Menge von Realisierungen (auch Stichprobe genannt) muß einem vorgegebenen Verteilungsgesetz einer Zufallszahl gehorchen. • Es zeigt sich, dass es genügt, eine im Intervall (0, 1) gleichverteilte Zufallszahl zu erzeugen. Mittels dieser Zufallszahl kann zum Beispiel eine normalverteilte Zufallszahl mit gegebenen Mittelwert (Mu) und Standardabweichung (Sigma) algorithmisch erzeugt werden. 2

Anforderungen an eine im Intervall (0, 1) gleichverteilte Zufallszahl • Die Wahrscheinlichkeit, dass eine Realisierung in einem Teilintervall von (0, 1) liegt, ist nur von der Länge des Teilintervalls abhängig. Salopp gesagt: jede Zahl in (0, 1) ist gleichwahrscheinlich. • Die Anordnung der Zufallszahlen hat keine typischen Merkmale, z. B. die Vorzeichen der Differenzen von aufeinanderfolgenden Zufallszahlen lassen keine typischen Muster erkennen. • Da es nur endliche viele Zustände eines Rechners gibt, muss ein solcher Algorithmus periodisch werden. Wir fordern deshalb, dass die Periodenlänge möglichst groß ist. • Ausgehend von gegebenen Startwerten (sogenannten Seed-Werten) muss eine große Anzahl von stochastisch unabhängigen Zufallszahlen zur Verfügung stehen. • Um bestimmte statistischen Methoden (wie z. B. die Varianzreduktion) anwenden zu können, müssen die zufälligen Prozesse einer Simulation reproduzierbar sein. 3

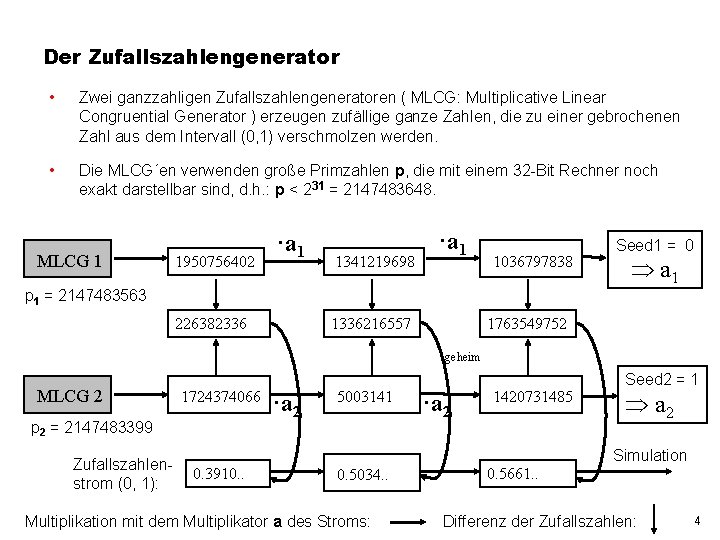
Der Zufallszahlengenerator • Zwei ganzzahligen Zufallszahlengeneratoren ( MLCG: Multiplicative Linear Congruential Generator ) erzeugen zufällige ganze Zahlen, die zu einer gebrochenen Zahl aus dem Intervall (0, 1) verschmolzen werden. • Die MLCG´en verwenden große Primzahlen p, die mit einem 32 -Bit Rechner noch exakt darstellbar sind, d. h. : p < 231 = 2147483648. MLCG 1 1950756402 ·a 1 1341219698 ·a 1 1036797838 p 1 = 2147483563 226382336 1336216557 Seed 1 = 0 a 1 1763549752 geheim MLCG 2 1724374066 p 2 = 2147483399 Zufallszahlenstrom (0, 1): ·a 2 5003141 ·a 2 1420731485 Seed 2 = 1 a 2 Simulation 0. 3910. . 0. 5034. . Multiplikation mit dem Multiplikator a des Stroms: 0. 5661. . Differenz der Zufallszahlen: 4

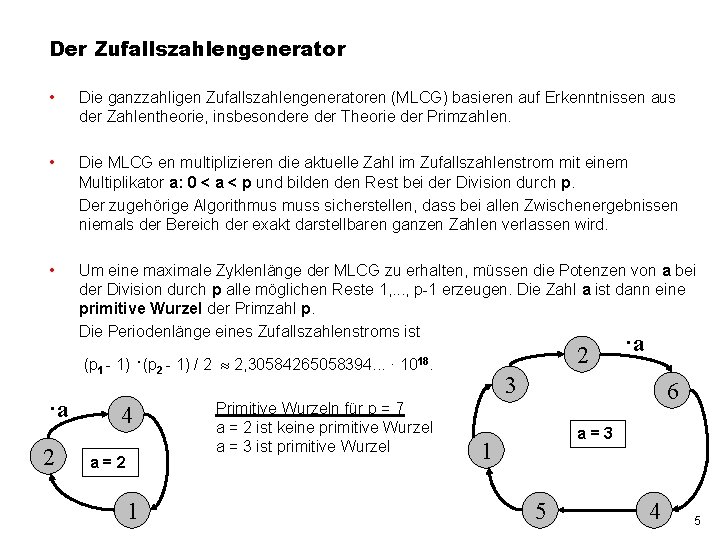
Der Zufallszahlengenerator • Die ganzzahligen Zufallszahlengeneratoren (MLCG) basieren auf Erkenntnissen aus der Zahlentheorie, insbesondere der Theorie der Primzahlen. • Die MLCG en multiplizieren die aktuelle Zahl im Zufallszahlenstrom mit einem Multiplikator a: 0 < a < p und bilden Rest bei der Division durch p. Der zugehörige Algorithmus muss sicherstellen, dass bei allen Zwischenergebnissen niemals der Bereich der exakt darstellbaren ganzen Zahlen verlassen wird. • Um eine maximale Zyklenlänge der MLCG zu erhalten, müssen die Potenzen von a bei der Division durch p alle möglichen Reste 1, . . . , p-1 erzeugen. Die Zahl a ist dann eine primitive Wurzel der Primzahl p. Die Periodenlänge eines Zufallszahlenstroms ist 2 (p 1 - 1) ·(p 2 - 1) / 2 2, 30584265058394. . . · 1018. ·a 2 4 a=2 1 Primitive Wurzeln für p = 7 a = 2 ist keine primitive Wurzel a = 3 ist primitive Wurzel ·a 3 6 a=3 1 5 4 5

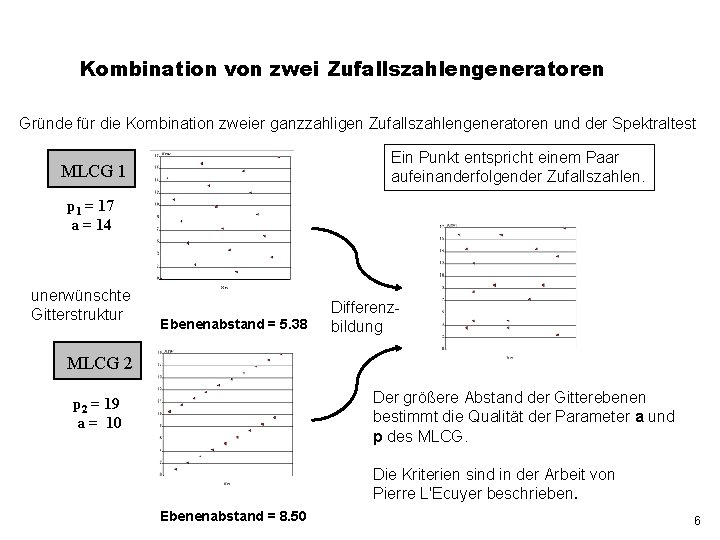
Kombination von zwei Zufallszahlengeneratoren Gründe für die Kombination zweier ganzzahligen Zufallszahlengeneratoren und der Spektraltest Ein Punkt entspricht einem Paar aufeinanderfolgender Zufallszahlen. MLCG 1 p 1 = 17 a = 14 unerwünschte Gitterstruktur Ebenenabstand = 5. 38 Differenzbildung MLCG 2 Der größere Abstand der Gitterebenen bestimmt die Qualität der Parameter a und p des MLCG. p 2 = 19 a = 10 Die Kriterien sind in der Arbeit von Pierre L'Ecuyer beschrieben. Ebenenabstand = 8. 50 6

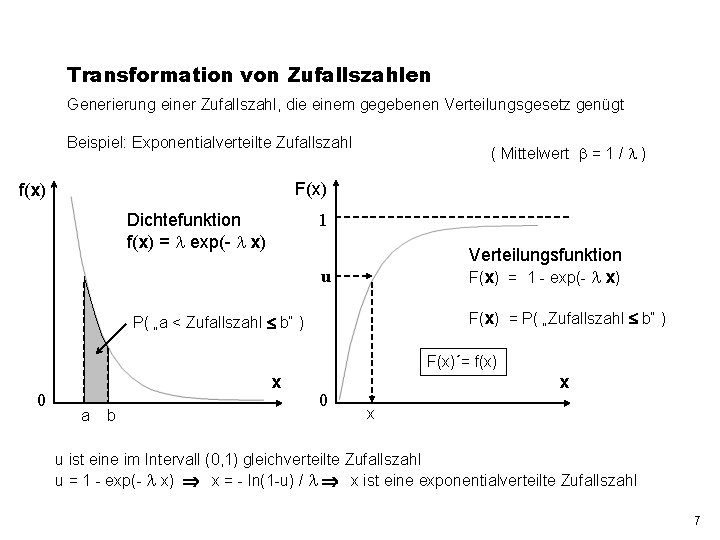
Transformation von Zufallszahlen Generierung einer Zufallszahl, die einem gegebenen Verteilungsgesetz genügt Beispiel: Exponentialverteilte Zufallszahl ( Mittelwert = 1 / ) F(x) f(x) 1 Dichtefunktion f(x) = exp(- x) Verteilungsfunktion F(x) = 1 - exp(- x) u F(x) = P( „Zufallszahl b“ ) P( „a < Zufallszahl b“ ) F(x)´= f(x) 0 x a b 0 x x u ist eine im Intervall (0, 1) gleichverteilte Zufallszahl u = 1 - exp(- x) x = - ln(1 -u) / x ist eine exponentialverteilte Zufallszahl 7

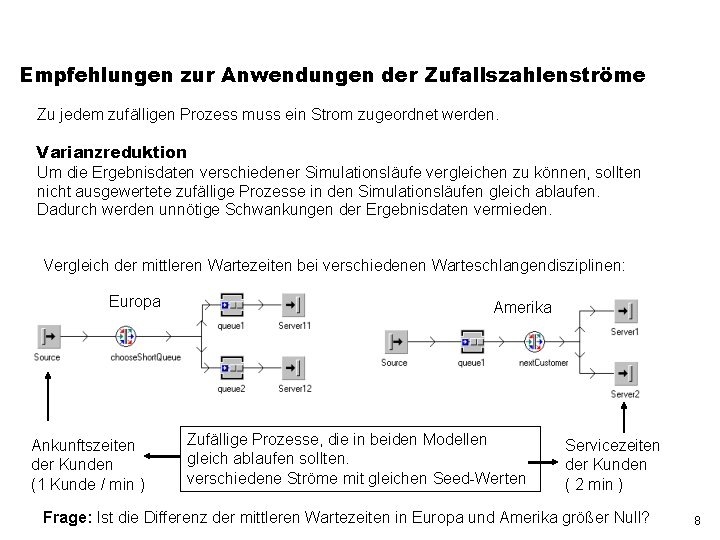
Empfehlungen zur Anwendungen der Zufallszahlenströme Zu jedem zufälligen Prozess muss ein Strom zugeordnet werden. Varianzreduktion Um die Ergebnisdaten verschiedener Simulationsläufe vergleichen zu können, sollten nicht ausgewertete zufällige Prozesse in den Simulationsläufen gleich ablaufen. Dadurch werden unnötige Schwankungen der Ergebnisdaten vermieden. Vergleich der mittleren Wartezeiten bei verschiedenen Warteschlangendisziplinen: Europa Ankunftszeiten der Kunden (1 Kunde / min ) Amerika Zufällige Prozesse, die in beiden Modellen gleich ablaufen sollten. verschiedene Ströme mit gleichen Seed-Werten Servicezeiten der Kunden ( 2 min ) Frage: Ist die Differenz der mittleren Wartezeiten in Europa und Amerika größer Null? 8

Bestimmung der Güte der Simulationsergebnisse Es genügt nicht, die Ergebnisse aus verschiedenen Simulationsläufen nur durch einen Mittelwert zusammenzufassen. Die Ergebnisse können nur dann sinnvoll interpretiert werden, wenn zu dem Mittelwert das zugehörige Konfidenzintervall (Vertrauensintervall) angegeben wird. Die Simulationsergebnisse sind auch Zufallszahlen, von denen man nur wenige Realisierungen beobachtet hat (Stichprobe). Konfidenzintervalle ermöglichen die Genauigkeit der Simulationsergebnisse zu schätzen. Ein Konfidenzintervall gibt an, in welchem Bereich sich der wahre Mittelwert der Zufallszahl mit einer gegebenen Wahrscheinlichkeit (Vertrauenswahrscheinlichkeit, Sicherheitsniveau) befindet. Eine Vergrößerung des Stichprobenumfanges führt bei gleicher Vertrauenswahrscheinlichkeit zu einer Verkleinerung des Konfidenzintervalls. Eine Vergrößerung der Vertrauenswahrscheinlichkeit führt bei gleichen Stichprobenumfang zu einer Vergrößerung des Konfidenzintervalls. 9

Konfidenzintervalle Gegeben ist eine Stichprobe einer (normalverteilten) Zufallszahl x. Beide Parameter der Zufallszahl sind unbekannt. n = Umfang der Stichprobe (z. B. Anzahl der Simulationsläufe) = Irrtumswahrscheinlichkeit des Konfidenzintervalls 1 - = Vertrauenswahrscheinlichkeit des Konfidenzintervalls (90%) m = Mittelwert der Stichprobe s = Standardabweichung der Stichprobe Das Konfidenzintervall [m-h, m+h] ist bestimmt durch P(„ m - h x m + h “) = P([m-h, m+h]) = 1 - . h = t(1 - /2, n-1) * s / n t(1 - /2, n-1) ist das Quantil der Student t-Verteilung mit n-1 Freiheitsgraden (aus Tabellen oder mit dem Modell Datafit. spp , Netzwerk. Statistical. Tools. Confidence bestimmen) Achtung: Die Excel-Funktion = KONFIDENZ(0, 1; C 16; 10) = 0, 1, Standardabweichung aus Zelle C 16, n = 10 geht von einer bekannten Standardabweichung der Zufallszahl x aus. 10

Konfidenzintervalle Beispiel: Differenz der mittleren Wartezeiten bei verschiedenen Warteschlangendisziplinen: Konfidenzintervall bei verschiedenen Ankunftsund Servicezeiten: [ -458 , 600 ] (m = 71) Mit einer Vertrauenswahrscheinlichkeit von 90 % kann man auf Grund dieser Simulationsstudie nicht entscheiden, ob die Wartezeiten in Europa oder Amerika kürzer sind. Konfidenzintervall bei gleichen Ankunfts- und Servicezeiten: [ 25 , 45 ] (m = 35) Der Mittelwert der Differenz der Wartezeiten in Europa und Amerika ist mit einer Wahrscheinlichkeit von 90 % zwischen 25 und 45 Sekunden. Streuungsdiagramme mit Wertepaare (Europa, Amerika) 11

Konfidenzintervalle und Stichprobenumfang Situation: Es liegt eine Stichprobe vom Umfang n vor. Die halbe Breite des Konfidenzintervalls ist h. Frage: Wie groß muss n* sein, um die halbe Breite des Konfidenzintervalls auf einem gewünschten Wert h* zu bringen? h = t(1 - /2, n -1) * s / n h* = t(1 - /2, n*-1) * s / n* n*/ n = (h / h*)2 t(1 - /2, n-1) liegt für n 10 zwischen 1. 282 und 3. 106. Auch wird sich die Standardabweichung mit wachsenden n kaum noch ändern. h 2 * n ist etwa konstant. Beispiel: Halbierung der Breite des Konfidenzintervalls ( h* / h = 0. 5 ) erfordert eine 4 -fach größere Stichprobe ( n* = 4 n ). Idee: J. Banks: „Output Analysis Capabilities of Simulation Software“, 1996 12

Abhängigkeit zwischen Simulationsergebnissen (x, y) = Cov(x, y) Kovarianz der Zufallszahlen x und y E[x] = Erwartungswert der Zufallszahl x (x, y) = E[ (x – E[x]) (y - E[y]) ] x und y sind stochastisch unabhängig: (x, y) = 0 (x, y) = Korrelationskoeffizient (x, y) = (x, y) / ( (x) (y) ) -1 (x, y) 1 Maß für die (lineare) Abhängigkeit von x und y, (x, y) = ± 1: linear abhängige Zufallszahlen x und y. 13

Literatur zur Simulation und Statistik • • J. Banks; J. S. Carson: „Discrete-Event System Simulation. “, Prentice--Hall 1984. Eine umfassende Einführung in die Mathematischen und statistischen Grundlagen mit Bezügen zur Simulation von Produktions- und Logistikprozessen. P. Bratley; B. L. Fox; L. E. Schrage: „A Guide to Simulation. “, Springer 1987. Kapitel 6 gibt einem umfassenden theoretischen Überblick zur Erzeugung von Zufallszahlen. H. Corsten: „Produktionswirtschaft. “, München, Wien 1994. Grundlagen zur Steuerung und Planung. Pierre L'Ecuyer: „Efficient and Portable Combined Random Number Generators. “ Comm of the ACM Vol 31, Number 6, 1988, p. 742 -750. Beschreibung der MLCG und Begründungen für die Wahl der Multiplikatoren und der verwendeteten Primzahlen. A. M. Law; W. D. Kelton: „Simulation Modeling & Analysis“, Mc. Graw-Hill, 1991. F. Liebl: „Simulation: Problemorientierte Einführung“, Oldenbourg Verlag 1995. Allgemeinverständliche Einführung in die diskrete Simulation mit zahlreichen Anweisungen und Hinweisen zur Durchführung von Simulationsprojekten. B. Page: „Diskrete Simulation: Eine Einführung mit Modula-2. “, Springer 1991. Statistische Verfahren werden ohne breite mathematische Abhandlungen allgemeinverständlich beschrieben. Hinweise zur Durchführung von Simulationsprojekten. K. Neumann; M. Morlock: „Operations Research. “, Hanser Verlag 1993. Mathematische Grundlagen in knapper Form mit zahlreichen algorithmischen Problemlösungen, Bezüge zur Produktion und Logistik. 14