ERT 1083 PHYSICAL CHEMISTRY FIRST LAW OF THERMODYNAMICS
















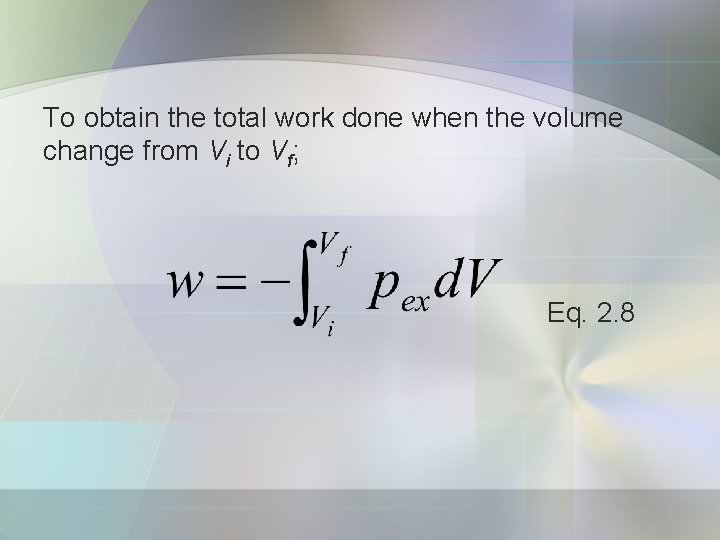

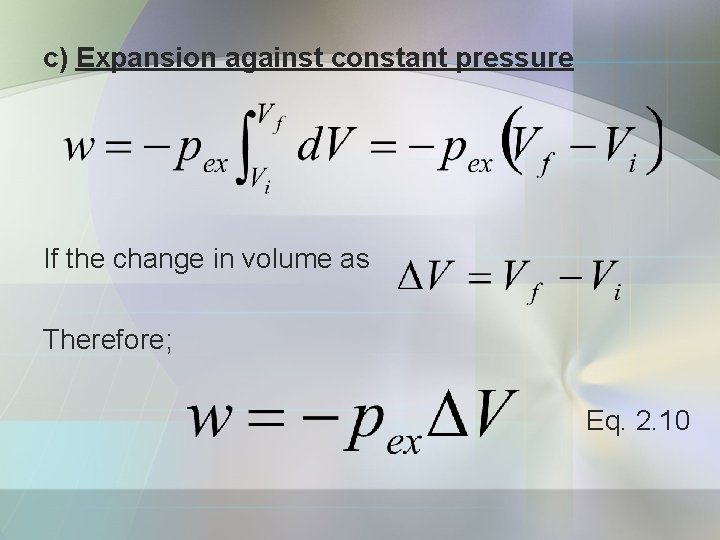
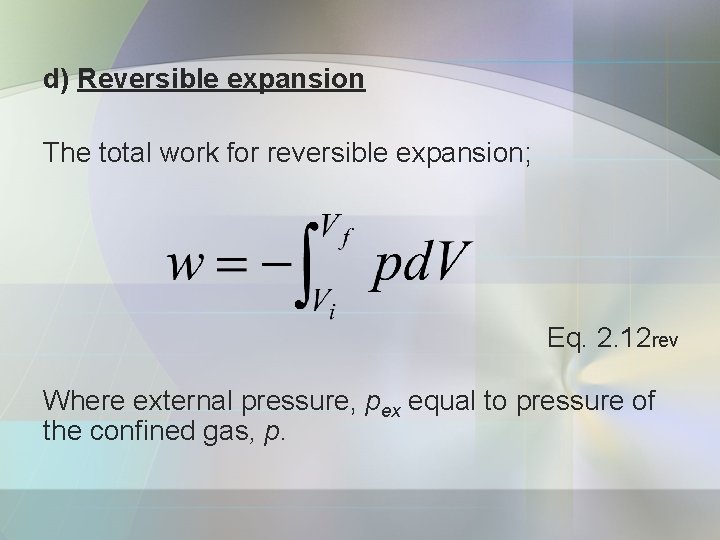







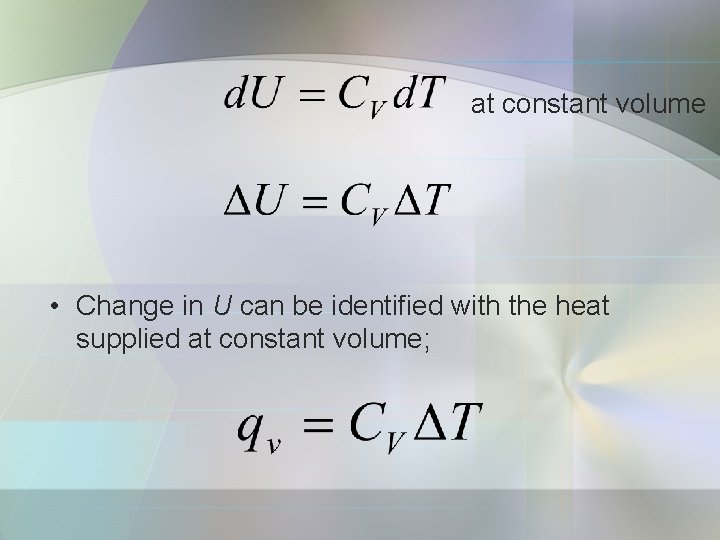

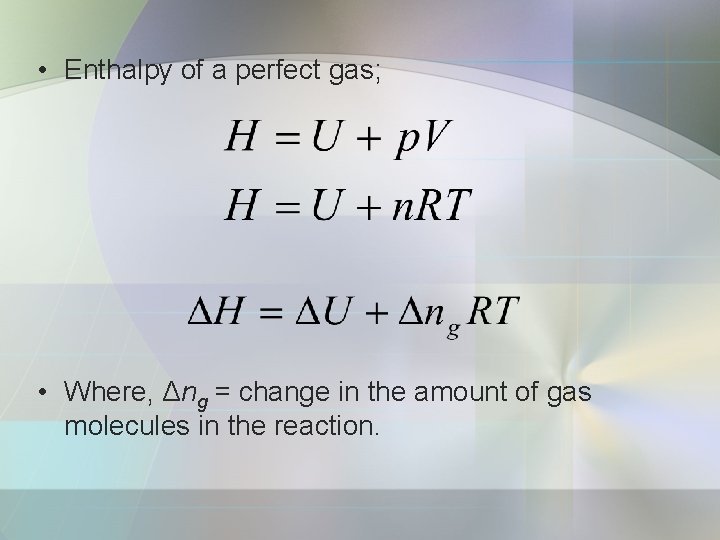






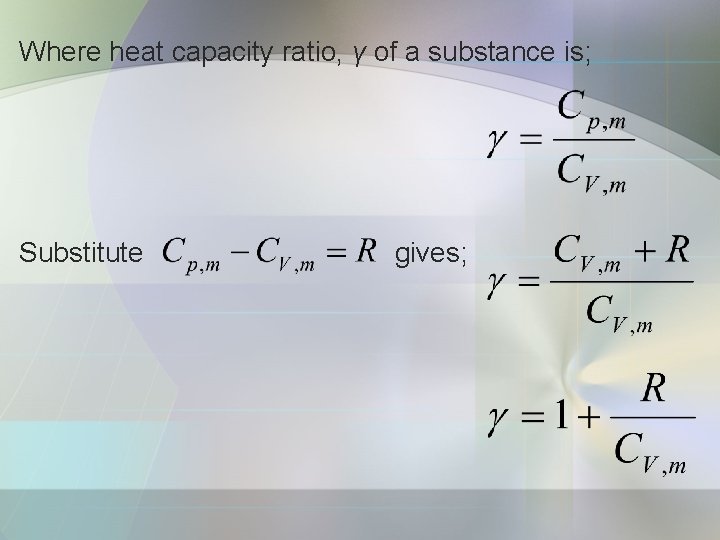
- Slides: 42

ERT 108/3 PHYSICAL CHEMISTRY FIRST LAW OF THERMODYNAMICS Prepared by: Pn. Hairul Nazirah Abdul Halim

Basic Concepts • Work, Heat & Energy • The First Law Work & Heat • Expansion Work • Heat Transaction • Enthalpy • Adiabatic Changes The First Law Thermochemistry • Standard Enthalpy Changes • Standard Enthalpy of Formation • The temperature dependence of reaction enthalpies

Thermodynamics • Thermodynamics is the study of the transformation of energy. Changes of energy in the form of heat in a system. • Thermodynamics deals with the interconversion of heat and other form of energy. • First Law of Thermodynamics: - energy can be converted from one form to another but it cannot be created or destroyed.

• Second Law of Thermodynamics explains why chemical process tends to favour one direction. • Chemical reactions occur with either the absorption or release of energy. • When a system does work or releases heat, its energy decreases. • It works on the law of conservation energy.

First Law of Thermodynamics • The release of energy can be used: - to provide heat when a fuel burns in an engine, - to generate electrical work when a chemical reaction pumps electron through the circuit.

Basic Concepts • The universe is divided into two parts; the system and its surroundings. • The system is the part of world such as reaction vessel, an engine, an electrochemical cell, etc. • The surroundings comprise the region outside the system where we make our measurements.

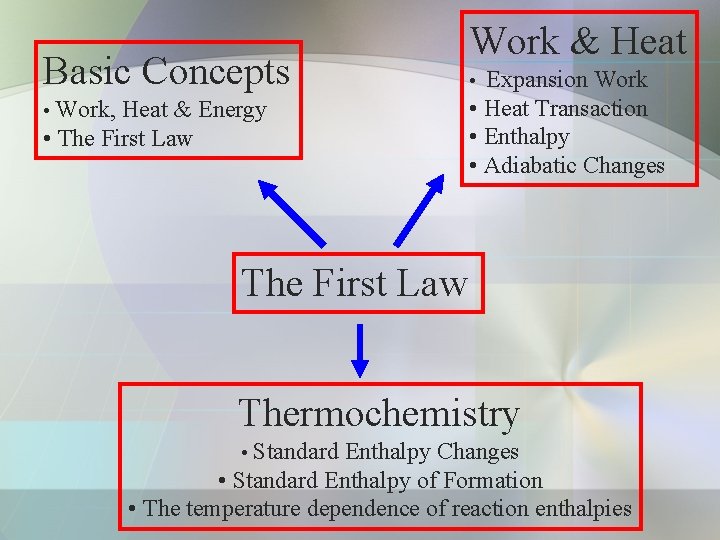
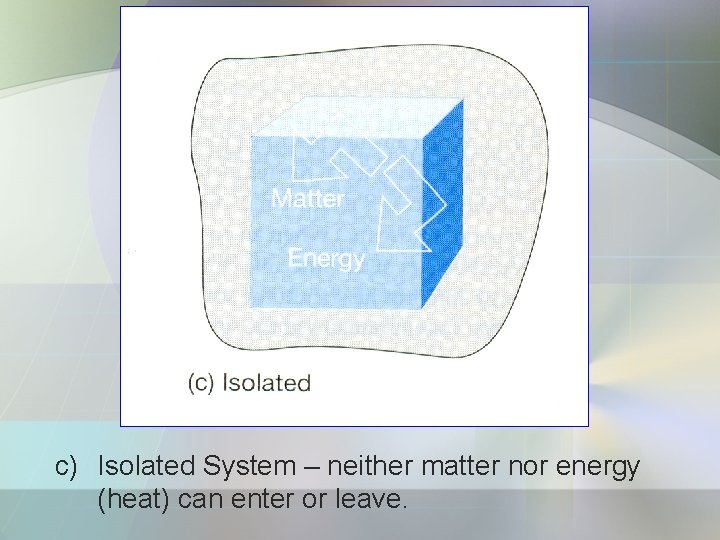
• System can be divided into 3: a) Open system – matter & energy can exchange with its surroundings. b) Closed System – energy can exchange with surroundings but it cannot exchange matter. c) Isolated System – is a closed system. - both energy and matter cannot exchange with its surroundings.

a) Open system – heat and matter can enter or leave.

b) Closed System – heat can enter or leave but not matter

c) Isolated System – neither matter nor energy (heat) can enter or leave.

Work, Heat and Energy • Work is done when an object is moved against an opposing force. • Example: the expansion of a gas that pushes out a piston and raises a weight. • Energy of a system is its capacity to do work. • When the system does work, the energy of the system is reduced.

• Exothermic process is a process that releases energy as heat. • Endothermic process is a process that absorbed energy as heat. • Example; vaporization of water

The First Law Internal energy is the total kinetic and potential energy of the molecules in the system. ΔU = the change in internal energy when a system changes from an initial state i with internal energy Ui to a final state f of internal energy Uf: • Internal energy, heat and work measured in Joule (J).

a) The conservation of energy Internal energy of a system may be changed either by doing work on the system or by heating it. The mathematical statement of First Law: Eq. 2. 2 ΔU = the change in internal energy q = the energy transferred as heat to a system w = work done on a system

b) The formal statement of the First Law “The work needed to change an adiabatic system from one specified state to another specified state is the same however the work is done. ” We can measure the change in the internal energy of a system by measuring the work needed to bring about the change in an adiabatic system: Eq. 2. 3

Work & Heat • • • Work is done when an object is moved against an opposing force. dw = the work done on a system; dq = energy supplied to a system as heat Eq. 2. 5

a) The general expression for work Work required to move an object a distance dz against an opposing force of magnitude F is Eq. 2. 6 -ve sign indicates that when the system moves an object against an opposite force, the internal energy of the system doing the work will decrease.

• Piston of area, A moves out through a distance, dz.

• If pex = external pressure, • Force acting on the outer piston is F = pex. A • When the system expands through a distance dz against external pressure pex; the work done is; • Adz is change in volume, d. V, therefore; Eq. 2. 7
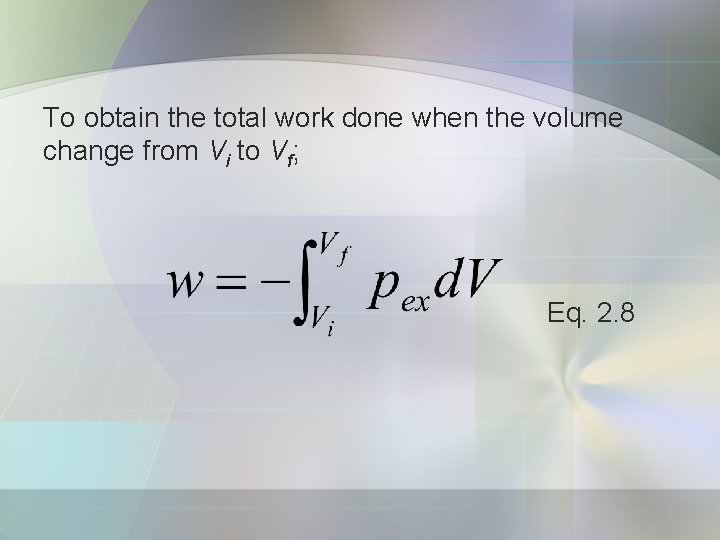
To obtain the total work done when the volume change from Vi to Vf; Eq. 2. 8

b) Free expansion • Free expansion means expansion against zero opposing force. • Occur when pex = 0 Eq. 2. 7 • If dw = 0, hence, overall w = 0. • No work is done when a system expands freely. • Occur when a system expands into a vacuum.
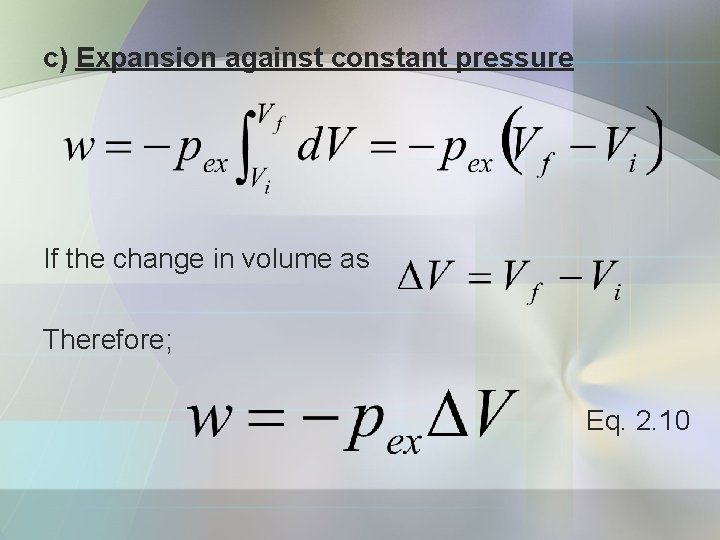
c) Expansion against constant pressure If the change in volume as Therefore; Eq. 2. 10
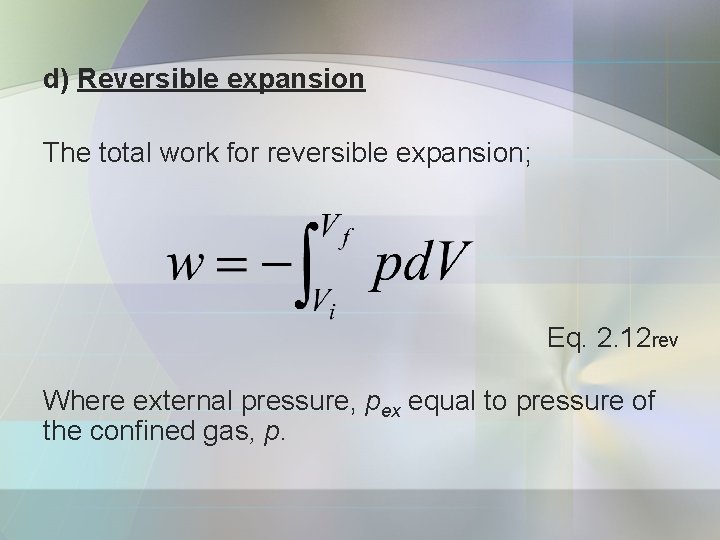
d) Reversible expansion The total work for reversible expansion; Eq. 2. 12 rev Where external pressure, pex equal to pressure of the confined gas, p.

e) Isothermal reversible expansion • Consider the isothermal, reversible expansion of a perfect gas. Eq. 2. 13 rev

Heat transactions The change in internal energy of a system is; Where; dwe = work in addition to the expansion work, dwexp. * dwe might be the electrical work of a driving current through a circuit.

At constant volume and no additional work; dwe = dwexp = 0; hence; Eq. 2. 15 Eq. 2. 16

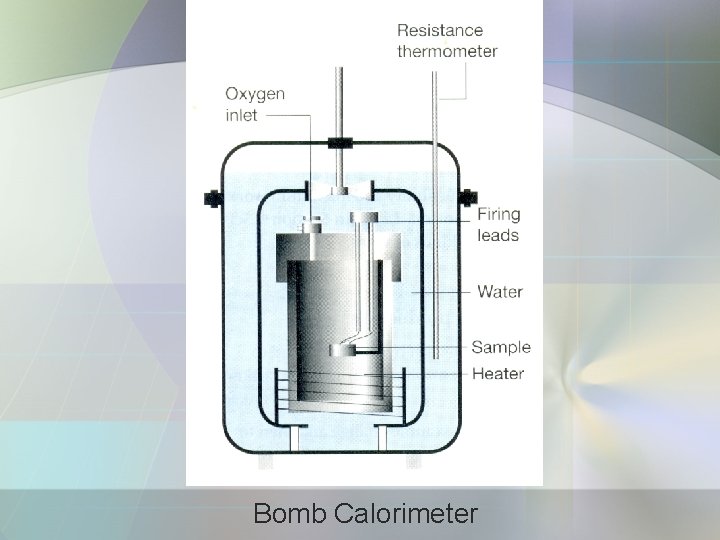
a) Calorimetry • The study of heat transfer during physical and chemical processes. • Calorimeter is a device for measuring the heat transferred. • Adiabatic bomb calorimeter – for measuring ΔU.

Bomb Calorimeter

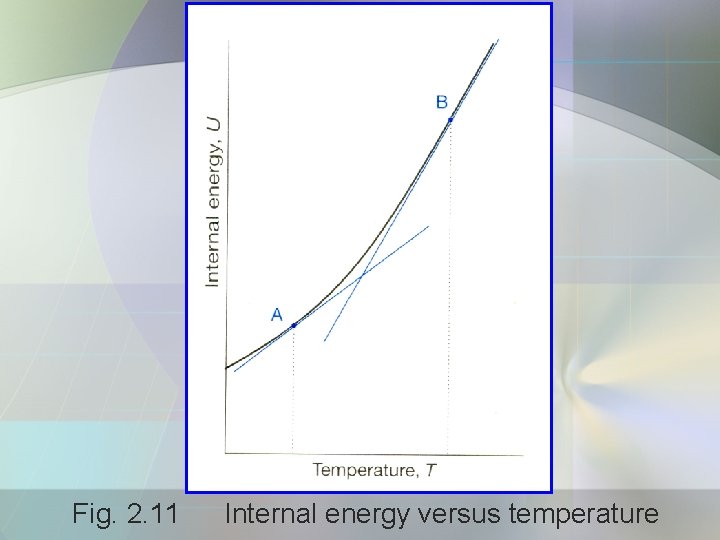
Heat Capacity • The internal energy, U of a substance increases when its temp. is raised. • Fig. 2. 11 internal energy is plotted against temp. • Heat capacity is the slope of tangent to the curve at any temp.

Fig. 2. 11 Internal energy versus temperature

• The heat capacity at constant volume, Cv is defined as: • It is a partial derivative. • Partial derivative is a slope calculated with all variables except one held constant. • In this case, the U varies with temp. , and the volume being held constant.

• The molar heat capacity at constant volume, Cv, m is the heat capacity per mole of material. (unit in J K-1 mol-1) • Specific heat capacity of a substance is the heat capacity of the sample divided by the mass (unit in J K-1 g-1) • A large heat capacity implies that for a given quantity of heat, gives small increase in temp.
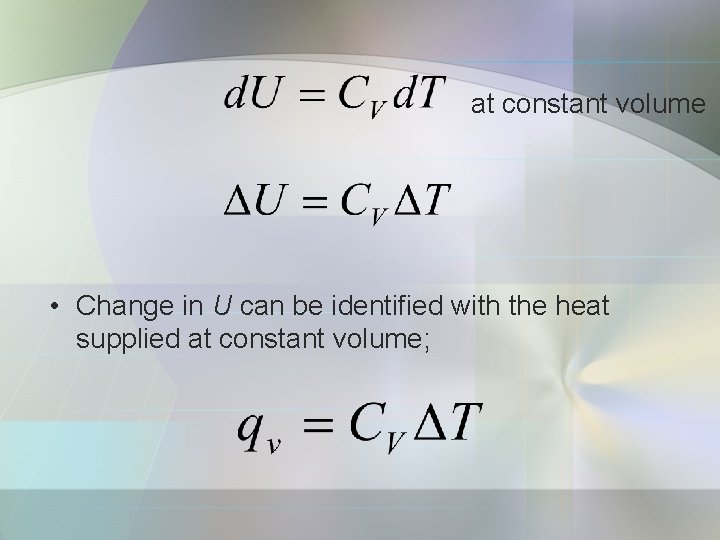
at constant volume • Change in U can be identified with the heat supplied at constant volume;

Enthalpy • Enthalpy, H is defined as: • Where; p = pressure of the system V = volume • Enthalpy is equal to the heat supplied at constant pressure;
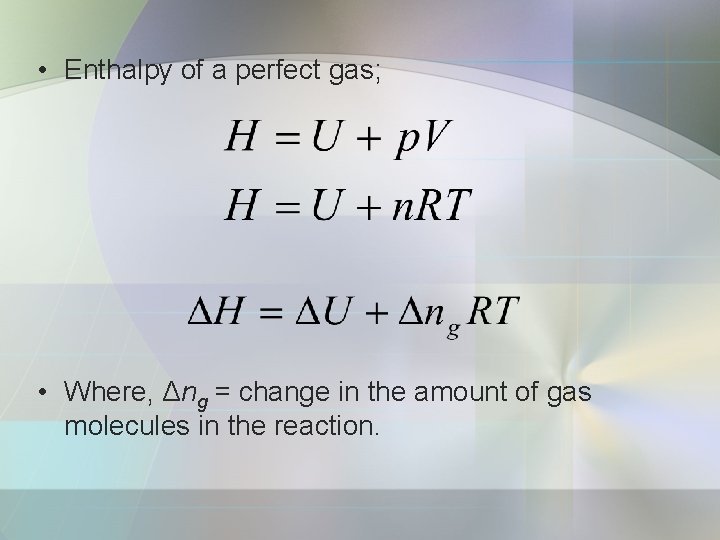
• Enthalpy of a perfect gas; • Where, Δng = change in the amount of gas molecules in the reaction.

c) The variation of enthalpy with temperature • Heat capacity at constant pressure, Cp; Eq. 2. 27 Eq. 2. 28 a Eq. 2. 28 b

Eq 2. 30 • The empirical parameters a, b and c are independent of temperature

The relation between heat capacities • Relation between two heat capacities of a perfect gas:

Adiabatic Changes a) Work of adiabatic change Eq. 2. 32 For adiabatic, q=0, Hence, Eq. 2. 33

• For adiabatic, reversible expansion the initial and final temperatures are related by; (Eq. 2. 34) rev (Eq. 2. 35)rev

b) Heat capacity ratio Consider the change in pressure that results from an adiabatic, reversible expansion of a perfect gas.
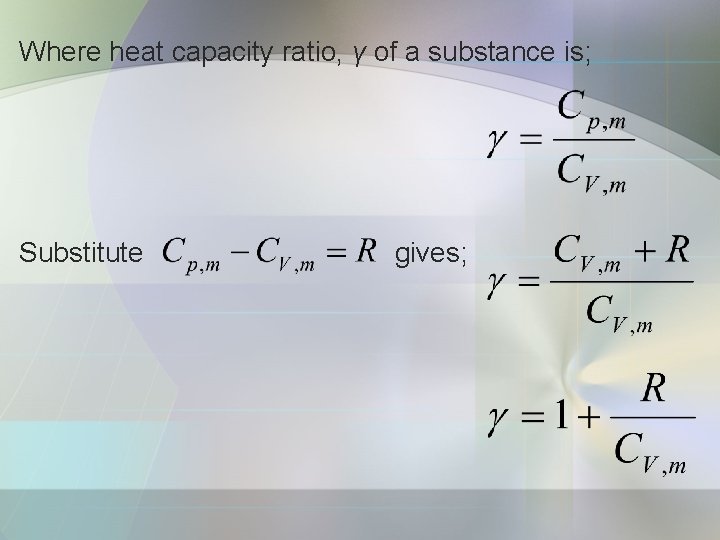
Where heat capacity ratio, γ of a substance is; Substitute gives;