EQUIVALENCIA Transformaciones de figuras manteniendo su rea FORMAS

  • Slides: 21
Download presentation
EQUIVALENCIA Transformaciones de figuras manteniendo su área

EQUIVALENCIA Transformaciones de figuras manteniendo su área

FORMAS EQUIVALENTES Dos figuras geométricas planas F y F´ son equivalentes si tienen igual

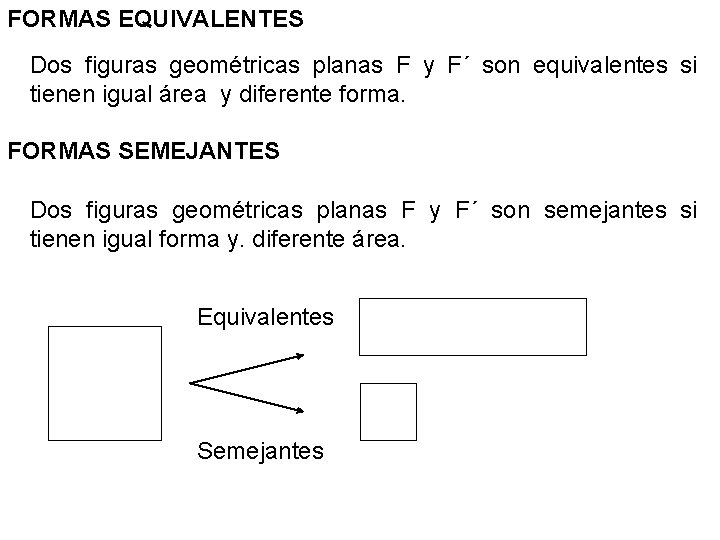
FORMAS EQUIVALENTES Dos figuras geométricas planas F y F´ son equivalentes si tienen igual área y diferente forma. FORMAS SEMEJANTES Dos figuras geométricas planas F y F´ son semejantes si tienen igual forma y. diferente área. Equivalentes Semejantes

FORMAS EQUIVALENTES • construcción de una figura plana F´ equivalentes de otra F Consiste

FORMAS EQUIVALENTES • construcción de una figura plana F´ equivalentes de otra F Consiste en resolver gráficamente la expresión algebraica: Área de la Figura Plana F´= Área de la Figura Plana F • Construcción de un polígono de (n-1) lados equivalente a otro a de n lados Consiste en sustituir un triángulo єF por otro triángulo ´ equivalente єF´, cuyo lado l ´єF´ esté alineado con otro lado l єF

Áreas ½ *b*h * R 2 l 2

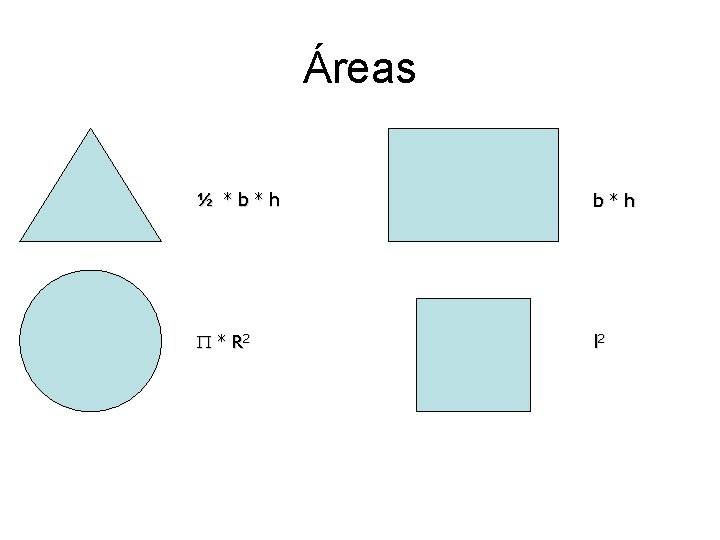
Áreas ½ *b*h * R 2 l 2

Cuadrado equivalente l 2 = b * h l 2 = ={ l 2

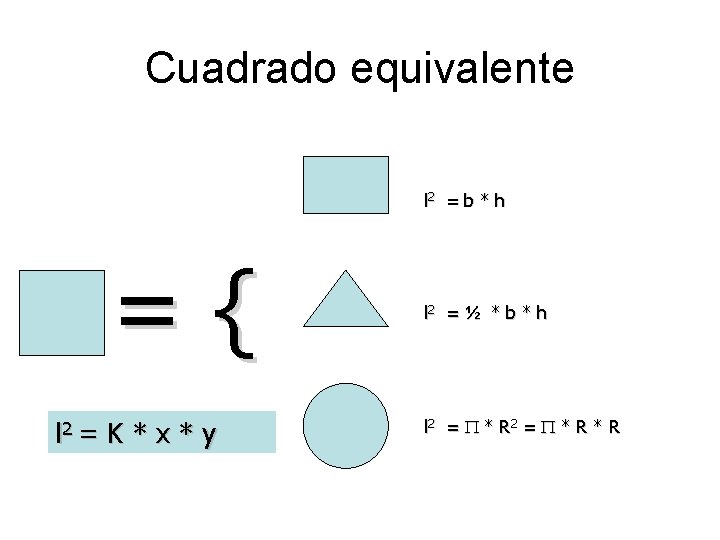
Cuadrado equivalente l 2 = b * h l 2 = ={ l 2 = ½ * b * h K*x*y l 2 = * R * R

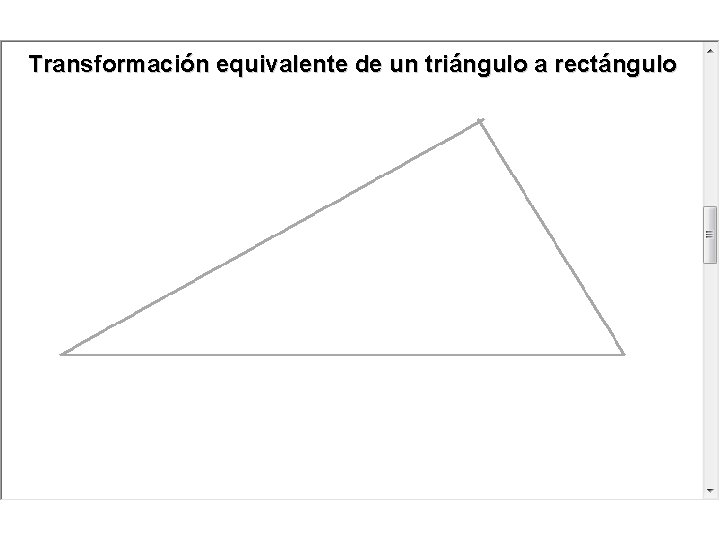
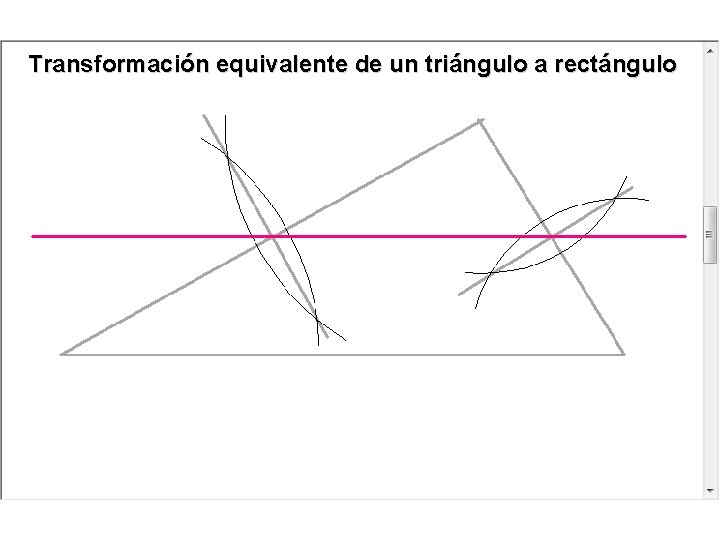
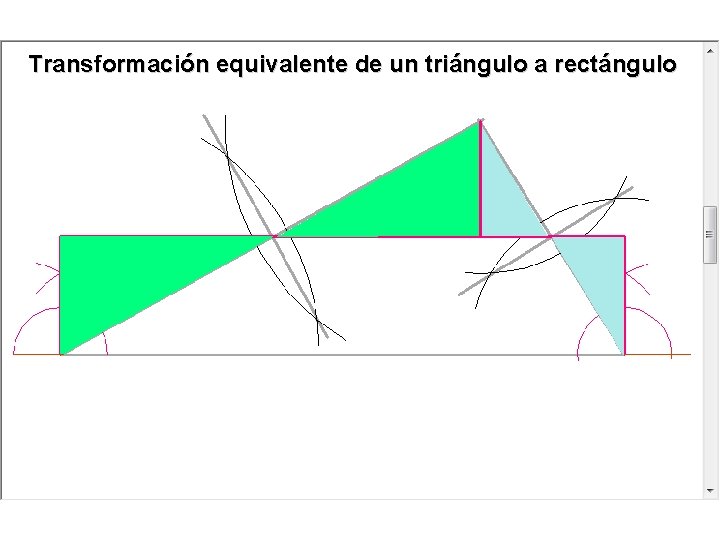
Transformación equivalente de un triángulo a rectángulo

Transformación equivalente de un triángulo a rectángulo

Transformación equivalente de un triángulo a rectángulo

Transformación equivalente de un triángulo a rectángulo

Transformación equivalente de un triángulo a rectángulo

Transformación equivalente de un triángulo a rectángulo

Transformación equivalente de un triángulo a rectángulo

Transformación equivalente de un triángulo a rectángulo

Transformación equivalente de un triángulo a rectángulo

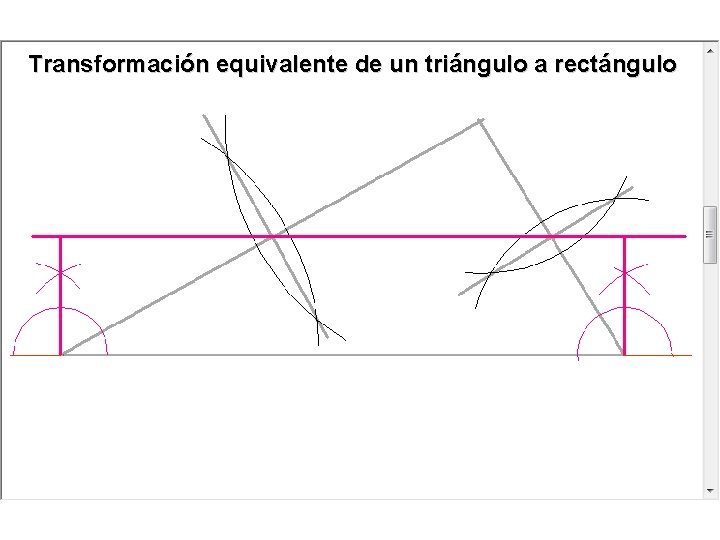
Transformación equivalente de un triángulo a rectángulo

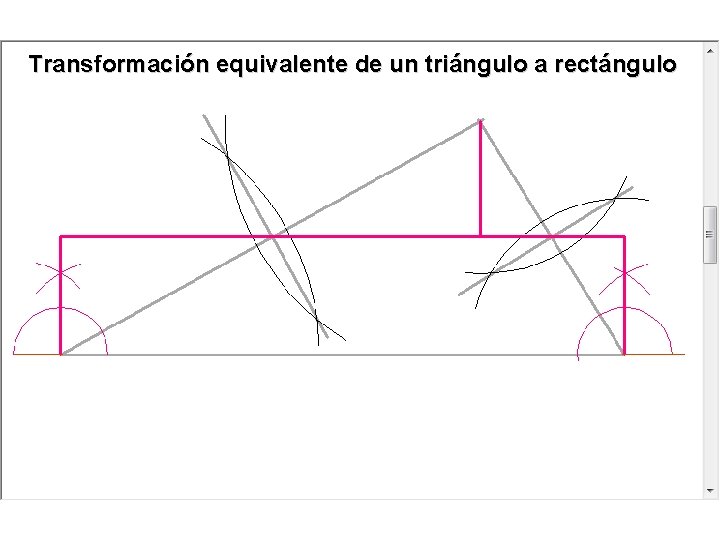
Transformación equivalente de un triángulo a rectángulo

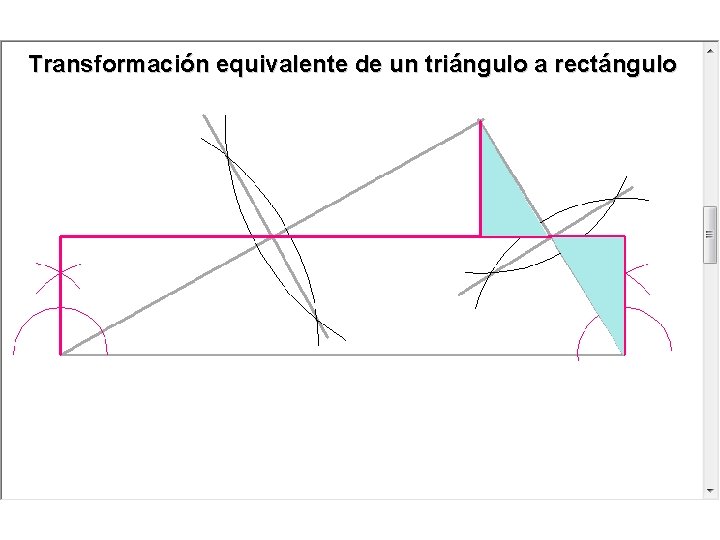
Transformación equivalente de un triángulo a rectángulo

Transformación equivalente de un triángulo a rectángulo

Transformación equivalente de un triángulo a rectángulo

Transformación equivalente de un triángulo a rectángulo

Transformación equivalente de un triángulo a rectángulo

Reducción de un polígono de n lados a otro de (n – 1) equivalente:

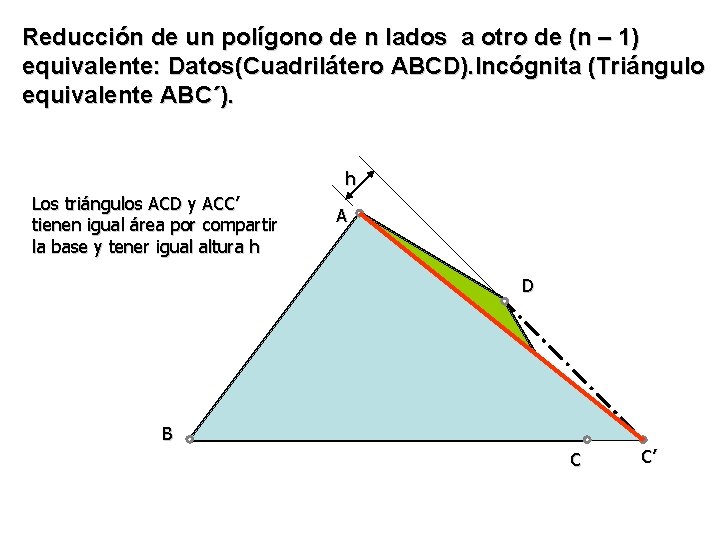
Reducción de un polígono de n lados a otro de (n – 1) equivalente: Datos(Cuadrilátero ABCD). Incógnita (Triángulo equivalente ABC´). h Los triángulos ACD y ACC’ tienen igual área por compartir la base y tener igual altura h A D B C C’

Formas equivalentes CP_6 P_02 Determinar el triángulo Isósceles equivalente al Pentágono regular A B

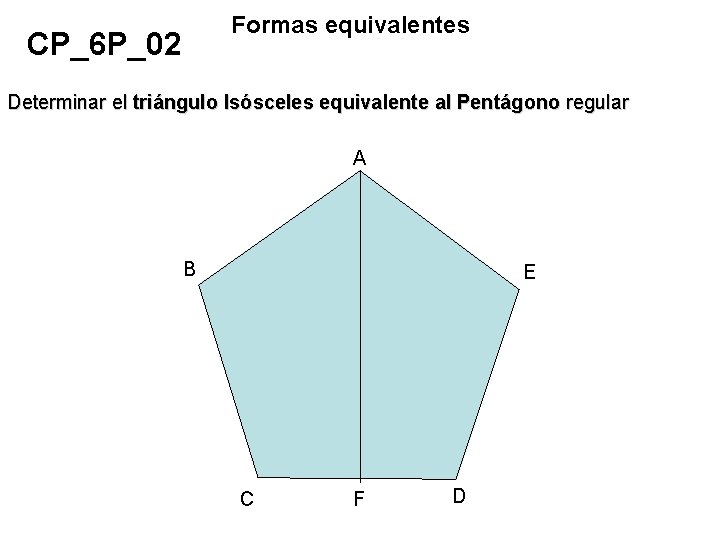
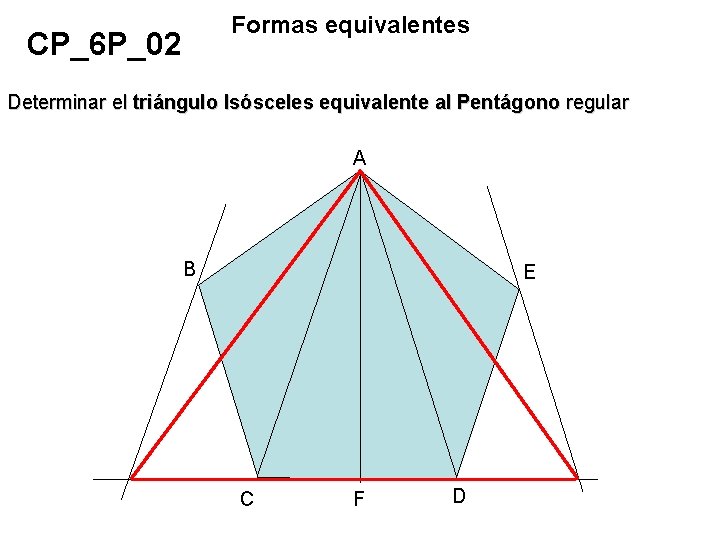
Formas equivalentes CP_6 P_02 Determinar el triángulo Isósceles equivalente al Pentágono regular A B E C F D

Formas equivalentes CP_6 P_02 Determinar el triángulo Isósceles equivalente al Pentágono regular A B

Formas equivalentes CP_6 P_02 Determinar el triángulo Isósceles equivalente al Pentágono regular A B E C F D

Determinar el CUADRADO equivalente al Pentágono regular A B E C F D

Determinar el CUADRADO equivalente al Pentágono regular A B E C F D

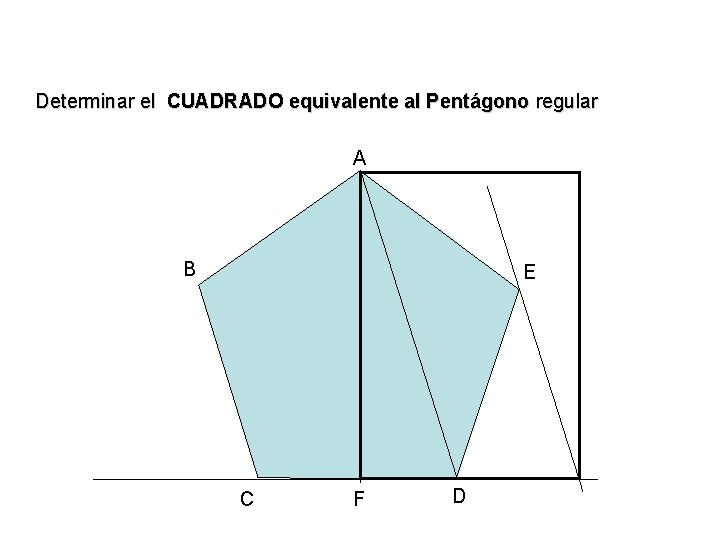
Determinar el CUADRADO equivalente al Pentágono regular A B E C F D

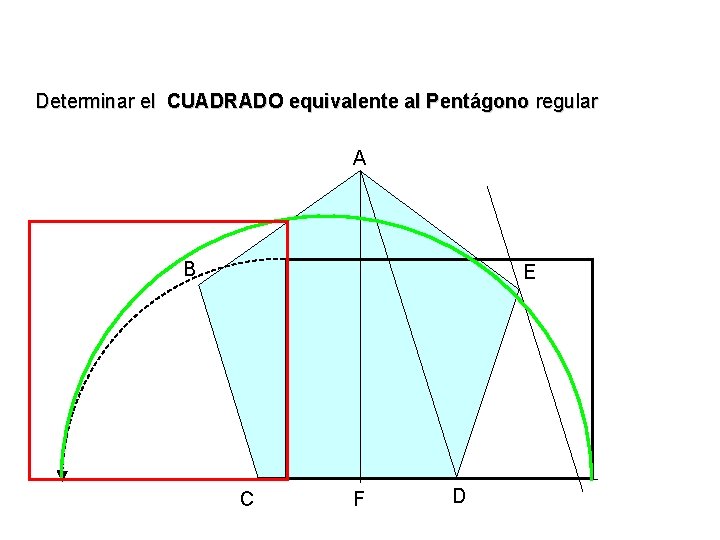
Determinar el CUADRADO equivalente al Pentágono regular A B E C F D

Ej: Determinar el cuadrado equivalente a l un rectángulo de lados b y h.

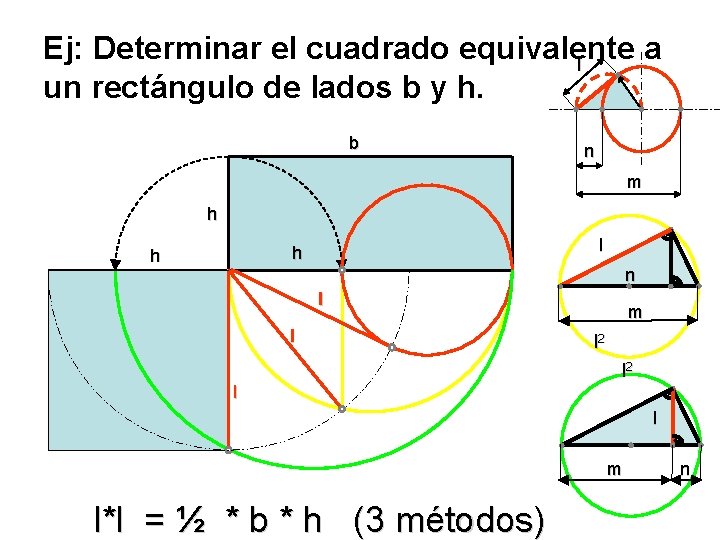
Ej: Determinar el cuadrado equivalente a l un rectángulo de lados b y h. b n m h l h h n l l m l 2 l l m l*l = ½ * b * h (3 métodos) n

Ej: Determinar el cuadrado equivalente a un triángulo dado de base b y altura

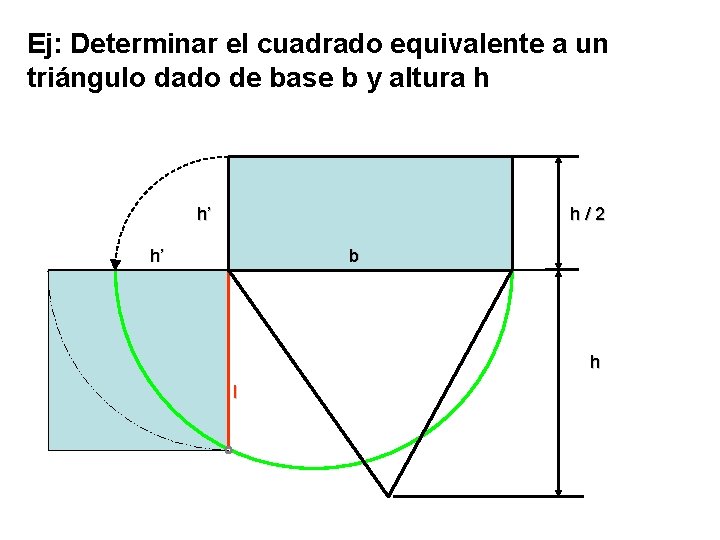
Ej: Determinar el cuadrado equivalente a un triángulo dado de base b y altura h h’ h/2 h’ b h l

• Ej: Determinar el cuadrado equivalente a un circulo dado de radio R

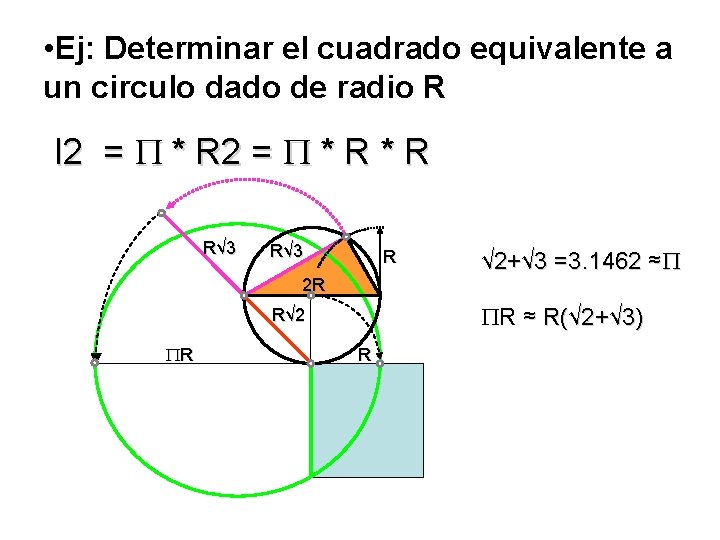
• Ej: Determinar el cuadrado equivalente a un circulo dado de radio R l 2 = * R * R R√ 3 R 2 R R ≈ R(√ 2+√ 3) R√ 2 R √ 2+√ 3 =3. 1462 ≈ R