Equivalence Class Testing In chapter 5 we saw

Equivalence Class Testing • In chapter 5, we saw that all four variations of boundary value testing are vulnerable to – gaps of untested functionality, and – significant redundancy, that results in extra effort • The mathematical notion of an equivalence class can potentially help this because – members of a class should be “treated the same” by a program – equivalence classes form a partition of the input space • Recall (from chapter 3) that a partition deals explicitly with – redundancy (elements of a partition are disjoint) – gaps (the union of all partition elements is the full input space)

Equivalence Class Testing • If you were testing the Triangle Program, would you use these test cases? – (3, 3, 3), (10, 10), (187, 187) • In Chapter 5, the normal boundary value test cases covered June 15 in five different years. Does this make any sense? • Equivalence class testing provides an elegant strategy to resolve such awkward situations.

Equivalence Class Testing • Use the mathematical concept of partitioning into equivalence classes to generate test cases for Functional (Black-box) testing • The key goals for equivalence class testing are similar to partitioning: 1. 2. completeness of test coverage lessen duplication of test coverage

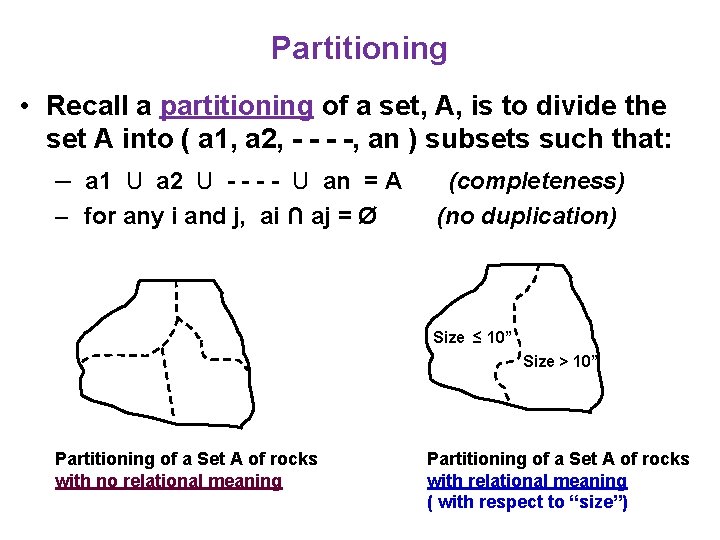
Partitioning • Recall a partitioning of a set, A, is to divide the set A into ( a 1, a 2, - -, an ) subsets such that: – a 1 U a 2 U - - U an = A (completeness) – for any i and j, ai ∩ aj = Ø (no duplication) Size ≤ 10” Size > 10” Partitioning of a Set A of rocks with no relational meaning Partitioning of a Set A of rocks with relational meaning ( with respect to “size”)

Equivalence Classes • Equivalence Relation, R, is a relation defined on the set A such that it is reflexive, transitive, and symmetric: let ε to mean an “element of” – Reflexive: z ε A, then (z, z) ε R – Symmetric: (a, b) ε R then (b, a) ε R, for all a, b in A – Transitive : (p, q) ε R and (q, r) ε R, then (p, r) ε R for all p, q, r in A • Equivalence class testing is the partitioning of the (often times, but not always) input variable’s value set into classes (subsets) using some equivalence relation. – Test cases are formed by selecting one value from each equivalence class. – Identifying the classes may be hard

Equivalence Class Test Cases • Consider a numerical input variable, i, whose values may range from -200 through +200. Then a possible partitioning of testing input variable, i, by 4 partitions may be: – -200 to -100 – – – • Define “same sign” as the equivalence relation, R, defined over the input variable’s value set, i = {-200 - -, 0, - -, +200}. Then one partitioning will be: – – – • -101 to 0 1 to 100 101 to 200 -200 to -1 (negative sign) 0 (no sign) 1 to 200 (positive sign) Let’s check if “same sign” relation, SS, is an equivalence relation: (let ‘ε’ be “element of”) – reflexive : -2 ε Input Variable then (-2, -2) ε SS – – symmetric : transitive: (3, 5) ε SS, then (5, 3) ε SS (-5, -7) ε SS and (-7, -200) ε SS , then (-5, -200) ε SS A sample equivalence test case “set” from the above “same sign” relation would be { -5; 0; 8 } where -5 is negative sign, 0 is no sign, 8 is positive sign

Forms of Equivalence Class Testing • “Traditional”—focus on invalid inputs • Normal: classes of valid values of inputs • Robust: classes of valid and invalid values of inputs • Weak: (single fault assumption) one from each class • Strong: (multiple fault assumption) one from each class in Cartesian Product • We compare these for a function of two variables, F(x 1, x 2) • Extension to problems with 3 or more variables is “obvious”.

“Traditional” Equivalence Class Testing • Programmer arrogance: – in the 1960 s and 1970 s, programmers often had very detailed input data requirements. – if input data didn’t comply, it was the user’s fault – the popular phrase—Garbage In, Garbage Out (GIGO) • Programs from this era soon developed defenses – (many of these programs are STILL legacy software) – as much as 75% of code verified input formats and values • “Traditional” equivalence class testing focuses on detecting invalid input. – (almost the same as our “weak robust equivalence class testing”)

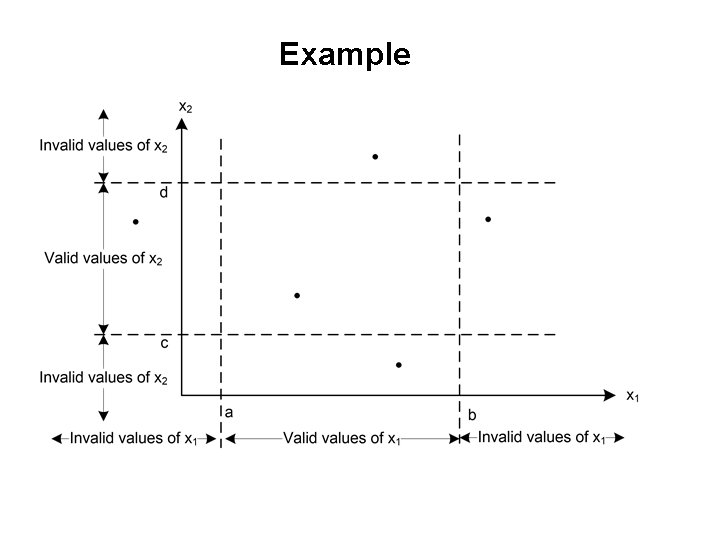
Example of Traditional Equivalence Class Testing • (only 2 -dimensions for drawing purposes) • easy to extend to more variables • F(x 1, x 2) has these classes. . . – – valid values of x 1: a ≤ x 1 ≤ b invalid values of x 1: x 1 < a, b < x 1 valid values of x 2: c ≤ x 2 ≤ d invalid values of x 2: x 2 < c, d < x 2 • Process – test F for valid values of all variables, – then test one invalid variable at a time – (note this makes the single fault assumption)

Example

Weak Normal Equivalence testing 1. Assumes the ‘single fault’ or “independence of input variables. ” – e. g. If there are 2 input variables, these input variables are independent of each other. 2. Partition the test cases of each input variable separately into one of the different equivalent classes. 3. Choose the test case from each of the equivalence classes for each input variable independently of the other input variable

Example of : Weak Normal Equivalence testing Assume the equivalence partitioning of input X is: 1 to 10; 11 to 20, 21 to 30 and the equivalence partitioning of input Y is: 1 to 5; 6 to 10; 11 to 15; and 16 to 20 X We have covered everyone of the 3 equivalence classes for input X. 30 20 10 1 Y 1 5 10 15 We have covered each of the 4 equivalence classes for input Y. 20 For ( x, y ) we have: (24, 2) (15, 8 ) ( 4, 13) (23, 17) General rule for # of test cases? What do you think? # of partitions of the largest set?

Strong Normal Equivalence testing • This is the same as the weak normal equivalence testing except for “multiple fault assumption” or “dependence among the inputs” • All the combinations of equivalence classes of the variables must be included.

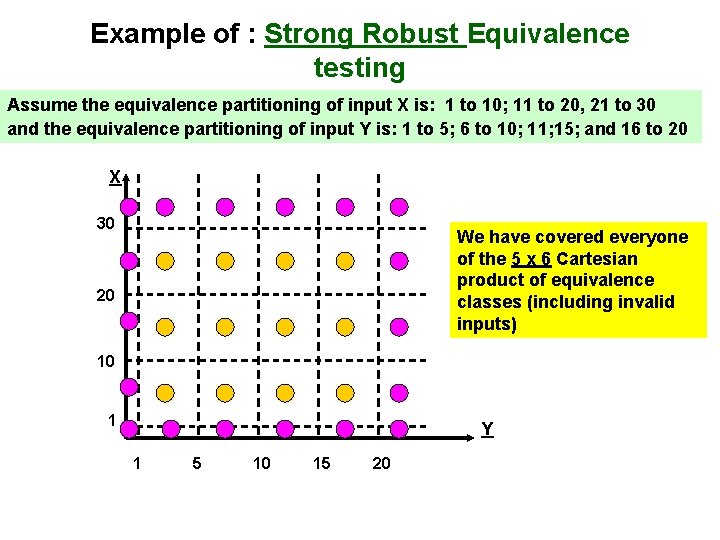
Example of : Strong Normal Equivalence testing Assume the equivalence partitioning of input X is: 1 to 10; 11 to 20, 21 to 30 and the equivalence partitioning of input Y is: 1 to 5; 6 to 10; 11; 15; and 16 to 20 X 30 We have covered everyone of the 3 x 4 Cartesian product of equivalence classes 20 10 1 Y 1 5 10 15 20 General rule for # of test cases? What do you think?

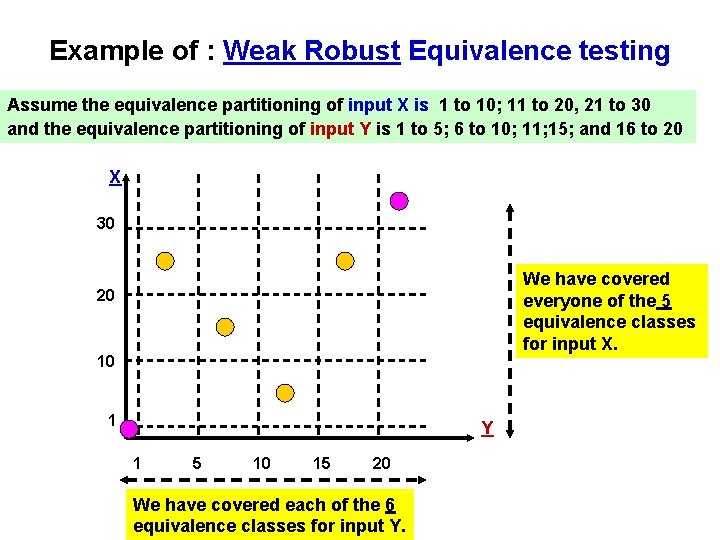
Weak Robust Equivalence testing • Up to now we have only considered partitioning the valid input space. • “Weak robust” is similar to “weak normal” equivalence test except that the invalid input variables are now considered. A note about considering invalid input is that there may not be any definition “specified” for the various, different invalid inputs - - - making definition of the output for these invalid inputs a bit difficult at times. (but fertile ground for testing)

Example of : Weak Robust Equivalence testing Assume the equivalence partitioning of input X is 1 to 10; 11 to 20, 21 to 30 and the equivalence partitioning of input Y is 1 to 5; 6 to 10; 11; 15; and 16 to 20 X 30 We have covered everyone of the 5 equivalence classes for input X. 20 10 1 Y 1 5 10 15 20 We have covered each of the 6 equivalence classes for input Y.

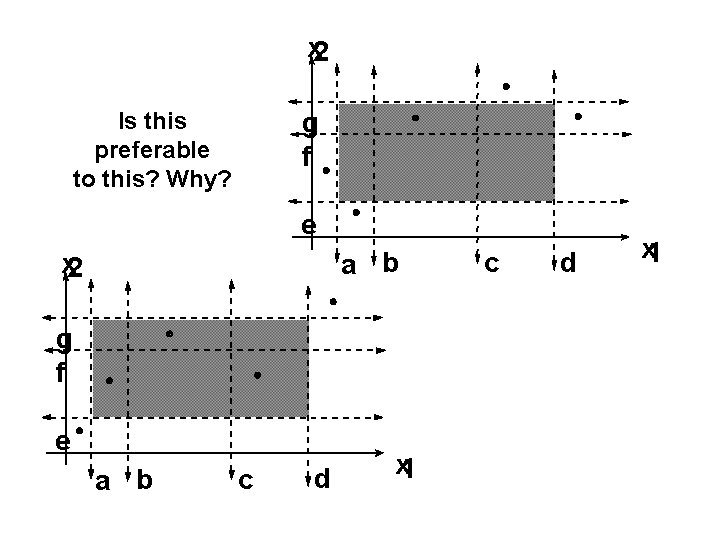
x 2 g f Is this preferable to this? Why? e a b x 2 g f e a b c d x 1

Strong Robust Equivalence testing • Does not assume “single fault” - - - assumes dependency of input variables • “Strong robust” is similar to “strong normal” equivalence test except that the invalid input variables are now considered.

Example of : Strong Robust Equivalence testing Assume the equivalence partitioning of input X is: 1 to 10; 11 to 20, 21 to 30 and the equivalence partitioning of input Y is: 1 to 5; 6 to 10; 11; 15; and 16 to 20 X 30 We have covered everyone of the 5 x 6 Cartesian product of equivalence classes (including invalid inputs) 20 10 1 Y 1 5 10 15 20

Equivalence class Definition • Note that the examples so far focused on defining input variables without considering the output variables. • For the earlier “triangle problem, ” we are interested in 4 questions: – – Is it a triangle? Is it an isosceles? Is it a scalene? Is it an equilateral? • We may define the input test data by defining the equivalence class through “viewing” the 4 output groups: – – input sides <a, b, c> do not form a triangle input sides <a, b , c> form an isosceles triangle input sides <a, b, c> form a scalene triangle input sides <a, b, c> form an equilateral triangle

Consider: Weak Normal Equivalence Test Cases to cover “Triangle” Problem Output “valid” inputs: 1<= a <= 200 1<= b <= 200 1<= c <= 200 and for triangle: a<b+c b<a+c c<b+a inputs a b c Not triangle 35 10 4 Equilateral 35 35 35 Isosceles 24 24 7 18 24 output Valid Inputs to get: Equilateral Not Triangle Isosceles Scalene 35

Strong Normal Equivalence Test Cases for Triangle Problem • Since there is no further sub-intervals inside the valid inputs for the 3 sides a, b, and c, and the 4 outputs are “independent, ” Strong Normal Equivalence is the same as the Weak Normal Equivalence for covering the outputs because the outputs are “independent” – You may want to look at Equilateral as the super set of Isosceles. But for this discussion, let’s consider them separate sets.

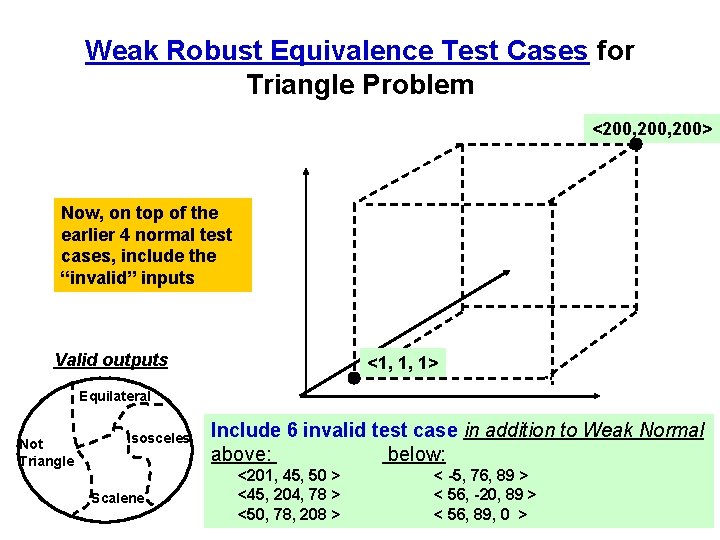
Weak Robust Equivalence Test Cases for Triangle Problem <200, 200> Now, on top of the earlier 4 normal test cases, include the “invalid” inputs Valid outputs <1, 1, 1> Equilateral Not Triangle Isosceles Scalene Include 6 invalid test case in addition to Weak Normal above: below: <201, 45, 50 > <45, 204, 78 > <50, 78, 208 > < -5, 76, 89 > < 56, -20, 89 > < 56, 89, 0 >

Strong Robust Equivalence Test Cases for Triangle Problem • Similar to Weak robust, but all combinations of “invalid” inputs must be included for the Strong Robust. • Look at the “cube” figure and consider the corners (two diagonal ones) a) Consider one of the corners <200, 200> : there a total of 23 combinatoric of valid-invalid but only (23 – 1) = 7 cases of “invalids” < 201, < 201, 50 , 201 > 50 > < 50 , 201, < 50, 50 , (50, 50 > 201 > 50) valid b) There will be 7 more “invalids” when we consider the other corner , <1, 1, 1 >: < 0, 0, 0 > < 0, 0, 5 > < 0, 10, 0 > < 0, 8, 10> <7, 0, 9 > <8, 0, 0 > <8, 9, 0 >

Next Day Program example • Here we have 3 input variables and may choose to have the sets defined as (without partitioning of days, month, or year): – Day : 1 through 31 days – Month: 1 through 12 – Year: 0001 through 3000 • In this case, for weak normal equivalence testing only needs 1 test case from each input: – (year; month; day) : (2001, 9, 23) • Clearly, this “non-partitioning” of the input gives very limited test case!

Next Day Program example (cont. ) • A more useful situation is to partition the 3 inputs. As an example: – – Day: 1 through 28 Day : 29 Day: 30 Day: 31 4 partitions of days – Month: those that have 31 days or {1, 3, 5, 7, 8, 10, 12} – Month: those that have 30 days or {4, 6, 9, 11} – Month: that has less than 30 days or {2} – Year: leap years between 0001 and 3000 – Year: non-leap years between 0001 and 3000 3 partitions of months 2 partitions of years

Next Day Problem example (cont. ) • Weak Normal equivalence Test Cases: • Number of test cases is driven by the # of partitions of the largest set, which in this case is the Days – has 4 partitions: (year, month, day): – – (leap year, 10, 8) (leap year, 4, 30) (non-leap year, 2, 31) (non-leap year, 7, 29) Without considering any relationship among the inputs and just mechanically following the rule How good is this set of test cases ? ? How valuable is the “generic” Weak Normal test Cases? --- Not Much!

Next Day Problem example (cont. ) • What about the Strong Normal case where we consider all the permutations of the previously partitioned 3 inputs? – We should have (2 years x 3 months x 4 days) = 24 test cases (leap year, 10, 5) (leap year, 10, 30) (leap year, 10, 31) (leap year, 10, 29) (non-leap year, 10, 5) (non-leap year, 10, 30) (non-leap year, 10, 31) (non-leap year, 10, 29) (leap year, 6, 5) (leap year, 6, 30) (leap year, 6, 31) (leap year, 6, 29) (non-leap year, 6, 5) (non-leap year, 6, 30) (non-leap year, 6, 31) (non-leap year, 6, 29) (leap year, 2, 5) (leap year, 2, 30) (leap year, 2, 31) (leap year, 2, 29) (non-leap year, 2, 5) (non-leap year, 2, 30) (non-leap year, 2, 31) (non-leap year, 2, 29) A little better than previous?

Next Day Problem example (cont. ) • What if we also consider the invalids, Weak Robust? – – – 31 < days; days < 1 12 < months; months < 1 3000 < year ; year < 0001 Then we need to include the following to the Weak Normal : ( valid year, 5, 45) ( valid year, 5, -5) ( valid year, 22, 30) ( valid year, 0, 15) ( 3500, 7, 20 ) ( 0000, 7, 15) combine ( 3500, 22, 45) into ( 0000, 0 , -5) Would you combine or leave them separately? Why?

Next Day Problem example (cont. ) • For Strong Robust, we need to consider and include all the permutations of the invalids to the Strong Normal: • 3 inputs, so there are 23 – 1=7 invalids each for high and for low, making a total of 14 more. high – – – – ( 3025, 45, 80) ( 3025, 45, 25) ( 3025, 7, 80) ( 3025, 7, 25) ( 2000, 45, 80) ( 2000, 45, 25) ( 2000, 7, 80) low ( 0000, -2, 0) ( 0000, -2, 15) ( 0000, 4 , 0) ( 0000, 4, 10) ( 2000, -2, 10) ( 2000, 4, 0)