EquitytoCredit Problem Philippe Henrotte ITO 33 and HEC

Equity-to-Credit Problem Philippe Henrotte ITO 33 and HEC Paris Equity-to-Credit Arbitrage Gestion Alternative, Evry, April 2004 http: //www. ito 33. com

Or how to optimally hedge your credit risk exposure with equity, equity options and credit default swaps http: //www. ito 33. com

Agenda n Traditional approach: diffusion + jump to default q q q n The notion of hazard rate Inhomogeneous model (local vol & hazard rate) Calibration and hedging problems More robust approach: jump-diffusion + stochastic volatility q q q Incomplete markets Homogeneous model Optimal hedging http: //www. ito 33. com

I – Traditional approach http: //www. ito 33. com

The equity price is the sole state variable n Structural models of the firm: Default is triggered by a bankruptcy threshold (certain or uncertain: Merton, KMV, Credit. Grades) n Reduced-form model: Default is triggered by a Poisson process of given intensity, a. k. a. “hazard rate” n Synthesis: making the hazard rate a function of the underlying equity value (and time) http: //www. ito 33. com

Default is a jump with intensity p(S, t) n Given no default before t: q q n n With probability (1 – pdt): no default With probability pdt: default Taking expectations (in the risk-neutral probability) Risk-free growth of the hedged portfolio http: //www. ito 33. com

In the risk-neutral world n n We solve the PDE opposite X is the jump in value of the hedge portfolio q q n Sdef is the recovery value of the underlying share Vdef is the recovery value of the derivative. Example : Convertible Bond Game is over upon default http: //www. ito 33. com

Example: Convertible Bond n n We recover a fraction of face value N We may have the right to convert at the recovery value of the underlying share http: //www. ito 33. com

Example: Credit Default Swap n n Credit protection buyer pays a premium u until maturity or default event We model this as asset U http: //www. ito 33. com

Example: Credit Default Swap n n n Credit protection seller pays a contingent amount at the time of default We model this as asset V is the insured security http: //www. ito 33. com

Example: Credit Default Swap n n R recovery rate CDS guarantees we recover par at maturity Simple closed forms when hazard rate is time dependent only: u is such that U(0, T) = (0, T) at inception http: //www. ito 33. com

Example: Equity Options n PDE for a Call under default risk n PDE for a Put under default risk http: //www. ito 33. com

Example: Equity Options n n n The jump to default generates an implied volatility skew Problem of the joint calibration to implied volatility data and credit spread data Calibrate (S, t) and p(S, t)? q In practice, we use parametric forms and p as S 0 http: //www. ito 33. com

Hedging (traditional approach) n n The hazard rate is expressed in the riskneutral world (calibrated from market data) Collapse of the bond floor (negative gamma) The delta-hedge presupposes that credit risk has been hedged with a CDS (or a put, …) Volatility hedge? http: //www. ito 33. com

What if there were a life after default? (Convertible bond case) n n Share does not jump to zero Issuer reschedules the debt Holder retains conversion rights It may not be optimal to convert a the time of default http: //www. ito 33. com

Switch to “default regime” n The default regime and the no-default regime are coupled through the Poisson transition n Two coupled PDEs, with different process parameters and different initial and boundary conditions http: //www. ito 33. com

Conclusion: the status of default/no default is the second state variable http: //www. ito 33. com

II – Incomplete Markets http: //www. ito 33. com

Incomplete markets n n n The state of no-default decomposes into subregimes of different diffusion components and different hazard rates This replaces (S, t) and p(S, t) with stochastic and stochastic p It turns the model into a homogenous model Markov transition matrix between regimes Stock jumps between regimes yield the needed correlations with vol and default http: //www. ito 33. com
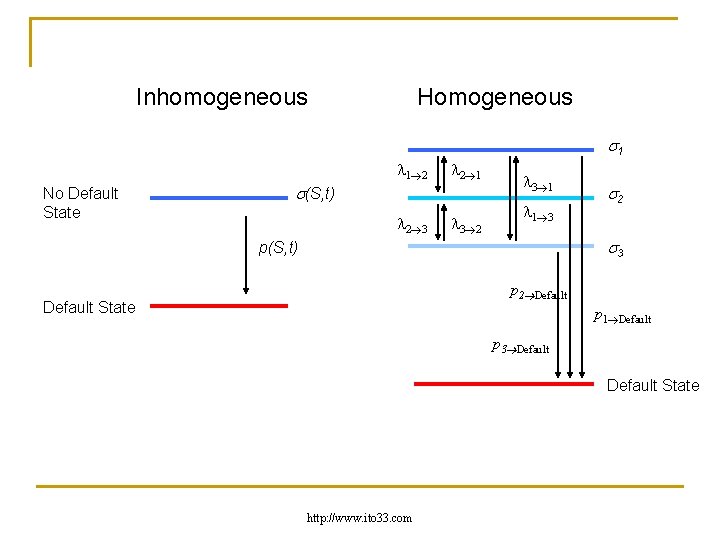
Inhomogeneous Homogeneous 1 1 2 No Default State 2 1 (S, t) 2 3 3 2 3 1 1 3 2 3 p(S, t) p 2 Default State p 1 Default p 3 Default State http: //www. ito 33. com

Incomplete markets n n In a Black-Scholes world without hedging, you can use the BS formula with any implied volatility value Perfect replication in the BS world imposes uniqueness: the implied volatility had better be the volatility of the underlying Under a general process (jump-diffusion, stochastic volatility, default process, etc. ), perfect replication is not possible… …and many non arbitrage pricing systems are possible (risk neutral probabilities) http: //www. ito 33. com

Pricing and calibration n If we wish to price one contingent claim relative to another, we can work in the riskneutral probability. This is called “calibration”: q q n Reverse engineer the prices of the Arrow. Debreu securities from the market prices of a given set of contingent claims Use the AD prices, or risk-neutral probability measure, to price a new contingent claim Whenever we wish to price a contingent claim “against the underlying” (by expressing the optimal hedging strategy), we have to work in the real probability http: //www. ito 33. com

Pricing through optimal hedge n n n The “fair value” of a contingent claim is the initial cost of its optimal dynamic replication strategy (for some optimality measure) This requires the knowledge of the historic or real probability measure… …while calibration only recovers a risk neutral probability We need to know the drift or the Sharpe ratio of the underlying The drift of the underlying drops out of the Black-Scholes pricing formula, not of the Black-Scholes world http: //www. ito 33. com

Calibration is just a pricing shortcut (It has nothing to say about hedging) n Examples: q q n Calibration of the risk-neutral default intensity function p(S, t) from the market prices of vanilla CDSs, or risky bonds Calibration of the risk-neutral jump-diffusion stochastic volatility process from the market prices of vanilla options To express the hedge, we have to transform back the risk-neutral probability into the real probability http: //www. ito 33. com

Hedging credit risk n Using the underlying only q q n Reducing the HERO q q n The notion of HERO Correlation between regimes and stock price Using the CDS to hedge credit risk and an option to hedge volatility risk (typically, hedging the CB) Using an out-of-the-money Put to hedge default risk (typically, hedging the CDS) Completing the market http: //www. ito 33. com

Tyco n n n Tyco, 3 February 2003 Stock price $16 Sharpe ratio 0. 3 Joint calibration of options and CDS Option prices fitted with a maximum error of 4 cents CDS up to 10 years http: //www. ito 33. com
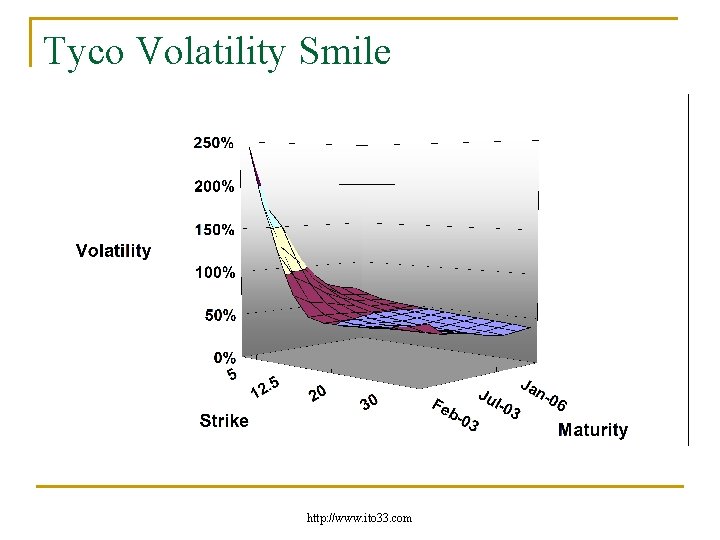
Tyco Volatility Smile http: //www. ito 33. com
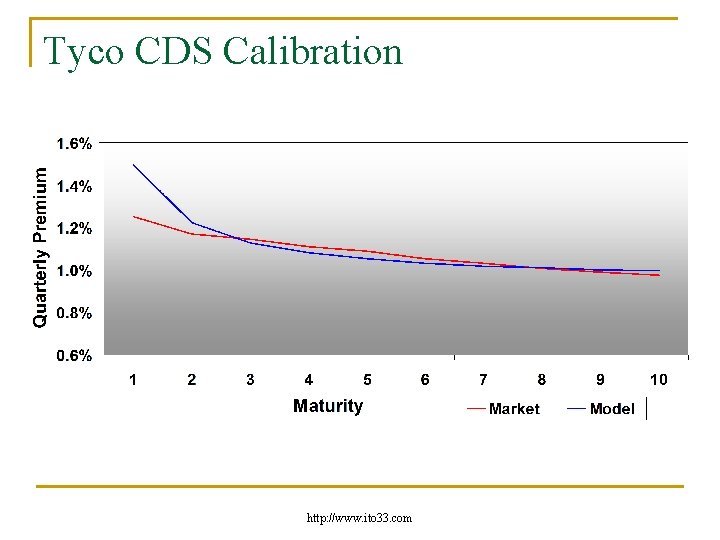
Tyco CDS Calibration http: //www. ito 33. com

Calibrated Regime Switching Model http: //www. ito 33. com

Tyco Convertible n n n Vanilla convertible bond Maturing in 5 years Conversion ratio 4. 38, corresponding to a conversion price of $22. 8 http: //www. ito 33. com

Optimal Dynamic Hedge n n n With the underlying alone HERO is $9. 8 If one uses the CDS with a maturity of 5 years on top of the underlying, the HERO falls to $5 If we add the Call with the same maturity and strike price $22. 5, the HERO falls down to a few cents and an almost exact replication is achieved http: //www. ito 33. com

Optimal Dynamic Hedge n n As a result, the convertible bond has been dynamically decomposed into an equity call option and a pure credit instrument This is the essence of the Equity to Credit paradigm http: //www. ito 33. com

References n n E. Ayache, P. Forsyth, and K. Vetzal: Valuation of Convertible Bonds with Credit Risk. The Journal of Derivatives, Fall 2003 E. Ayache, P. Forsyth, and K. Vetzal: Next Generation Models for Convertible Bonds with Credit Risk. Wilmott, December 2002 E. Ayache, P. Henrotte, S. Nassar, and X. Wang: Can Anyone Solve the Smile Problem? . Wilmott magazine, January 2004 P. Henrotte: Pricing and Hedging in the Equity to Credit Paradigm. FOW, January 2004 http: //www. ito 33. com
- Slides: 33