Equations in Simple Regression Analysis The Variance The




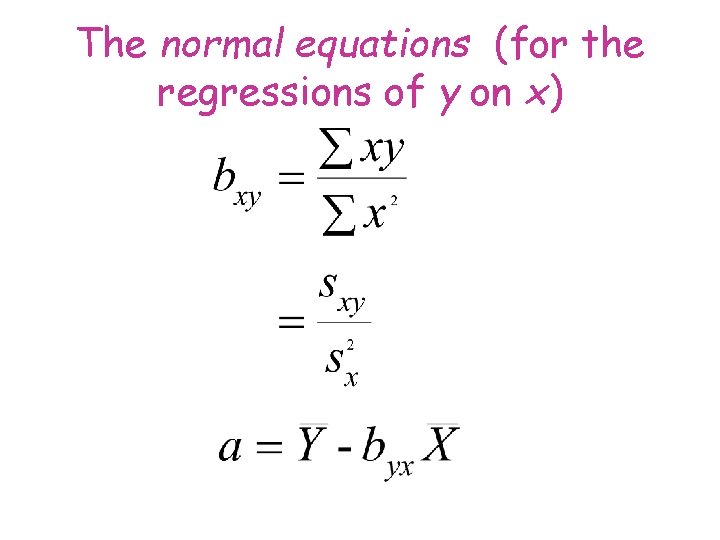

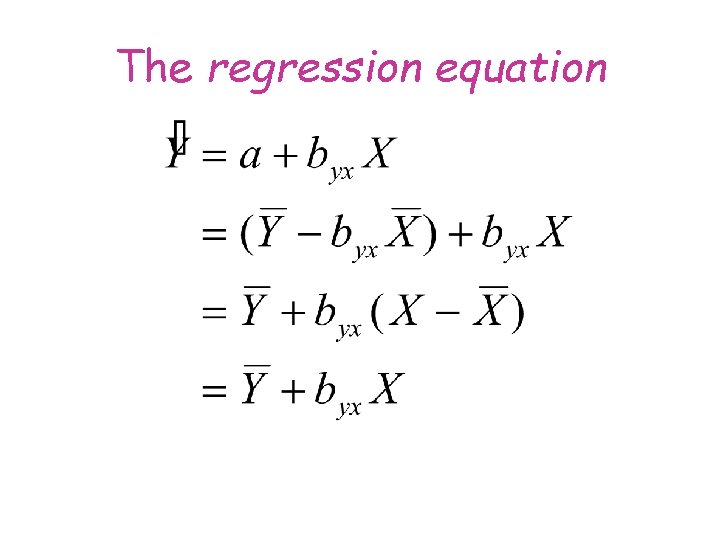


















- Slides: 26

Equations in Simple Regression Analysis

The Variance

The standard deviation

The covariance

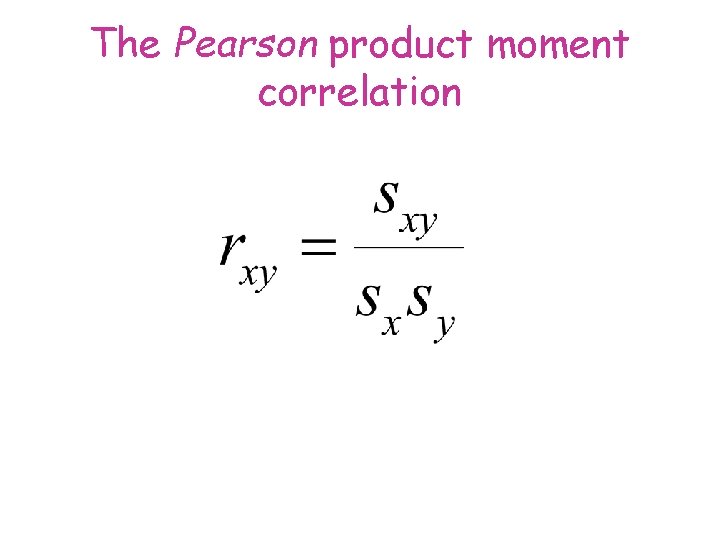
The Pearson product moment correlation
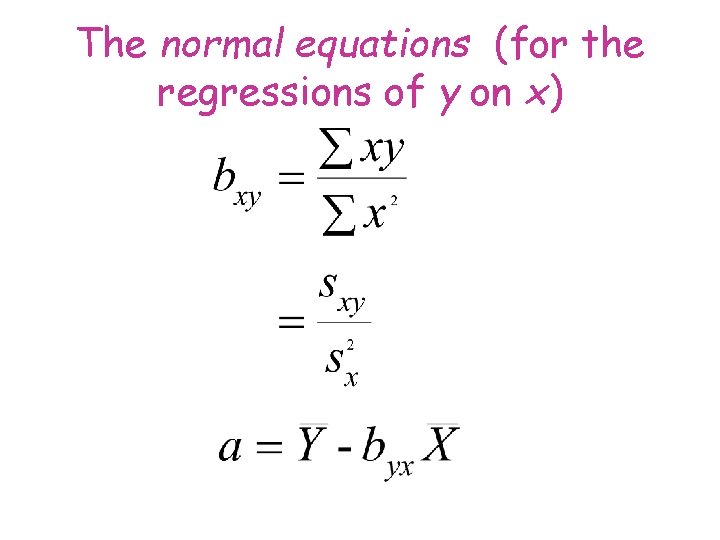
The normal equations (for the regressions of y on x)

The structural model (for an observation on individual i)
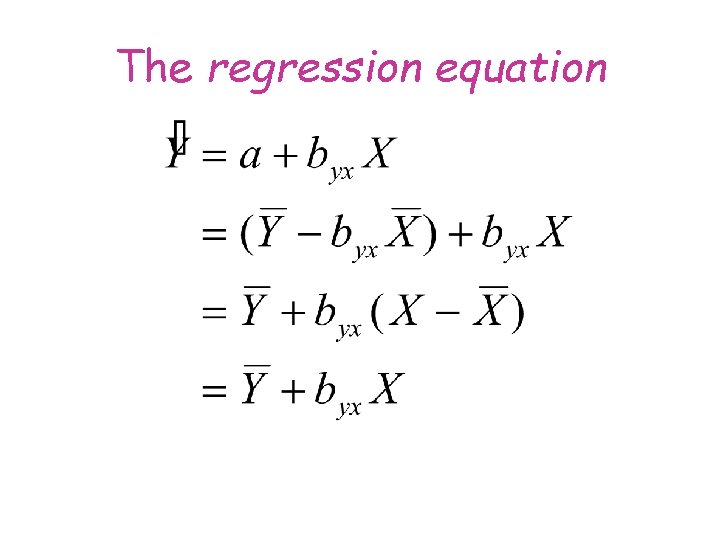
The regression equation

Partitioning a deviation score, y

Partitioning the sum of squared deviations (sum of squares, SSy)

Calculation of proportions of sums of squares due to regression and due to error (or residual)

Alternative formulas for computing the sums of squares due to regression

Test of the regression coefficient, byx, (i. e. test the null hypothesis that byx = 0) First compute the variance of estimate

Test of the regression coefficient, byx, (i. e. test the null hypothesis that byx = 0) Then obtain the standard error of estimate Then compute the standard error of the regression coefficient, Sb

The test of significance of the regression coefficient (byx) The significance of the regression coefficient is tested using a t test with (N-k-1) degrees of freedom:

Computing regression using correlations The correlation, in the population, is given by The population correlation coefficient, ρxy, is estimated by the sample correlation coefficient, rxy

Sums of squares, regression (SSreg) Recalling that r 2 gives the proportion of variance of Y accounted for (or explained) by X, we can obtain or, in other words, SSreg is that portion of SSy predicted or explained by the regression of Y on X.

Standard error of estimate From SSres we can compute the variance of estimate and standard error of estimate as (Note alternative formulas were given earlier. )

Testing the Significance of r The significance of a correlation coefficient, r, is tested using a t test: With N-2 degrees of freedom.

Testing the difference between two correlations To test the difference between two Pearson correlation coefficients, use the “Comparing two correlation coefficients” calculator on my web site.

Testing the difference between two regression coefficients This, also, is a t test: Where was given earlier. When the variances, , are unequal, used the pooled estimate given on page 258 of our textbook.

Other measures of correlation Chapter 10 in the text gives several alternative measures of correlation: Point-biserial correlation Phi correlation Biserial correlation Tetrachoric correlation Spearman correlation

Point-biserial and Phi correlation These are both Pearson Product-moment correlations The Point-biserial correlation is used when on variable is a scale variable and the other represents a true dichotomy. For instance, the correlation between an performance on an item—the dichotomous variable—and the total score on a test—the scaled variable.

Point-biserial and Phi correlation The Phi correlation is used when both variables represent a true dichotomy. For instance, the correlation between two test items.

Biserial and Tetrachoric correlation These are non-Pearson correlations. Both are rarely used anymore. The biserial correlation is used when one variable is truly a scaled variable and the other represents an artificial dichotomy. The Tetrachoric correlation is used when both variables represent an artificial dichotomy.

Spearman’s Rho Coefficient and Kendall’s Tau Coefficient Spearman’s rho is used to compute the correlation between two ordinal (or ranked) variables. It is the correlation between two sets of ranks. Kendall’s tau (see pages 286 -288 in the text) is also a measure of the relationship between two sets of ranked data.