Equations and Inequalities A6 Solve Linear Inequalities ACT






























- Slides: 31

Equations and Inequalities A-6 Solve Linear Inequalities

ACT WARM-UP n If 11 + 3 x = 56, then 5 x = ? n A) 15 B) 35 C) 45 D) 75 E) 105 n Solve for x. Since x = 15, then 5 x = 5(15) or D) 75.

Objectives n Solve and Graph Linear Inequalities n Solve and Graph Compound Inequalities

Essential Question How are the rules for solving linear inequalities similar to those for solving linear equations, and how are they different?

A linear inequality is a statement that compares two expressions by using the symbols <, >, ≤, ≥, or ≠. A solution of an inequality is the set of all points that satisfy the inequality and makes it a true statement when you substitute the number(s) for the variable. The graph of an inequality consists of all points on a number line that represent solutions. The properties of equality are true for inequalities, with one important difference. If you multiply or divide both sides by a negative number, you must reverse the inequality symbol.

REMEMBER! Use an open circle with an arrow to the left for < and an arrow to the right for >. Use a closed circle (solid dot) with an arrow to the left for ≤ and an arrow to the right for ≥. Subtracting a number is the same as adding its inverse, i. e. subtracting 5 is the same as adding − 5.

Solve Graph the solution set on a number line. Answer using interval notation. Original inequality Add – 4 y to each side. Simplify. Add – 2 to each side. Simplify. Rewrite with y first using symmetry.

Answer: Any real number greater than – 5 is a solution of this inequality. An open circle means that Interval notation: (− 5, ∞) this point is not included in the solution set.

Solve Graph the solution set on a number line. Answer in interval notation.

Multiplying or dividing each side of an inequality by a positive number does not change the truth of the inequality. However, multiplying or dividing each side of an inequality by a negative number requires that the order of the inequality be reversed. For example, to reverse ≤, replace it with ≥.

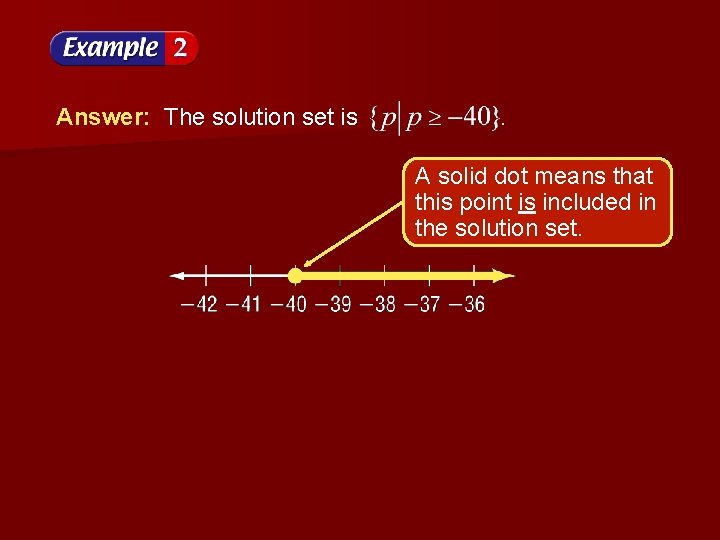
Solve Graph the solution set on a number line. Answer in set-builder notation. Original inequality Divide each side by – 0. 3, reversing the inequality symbol. – 40 p p – 40 Simplify. Rewrite with p first.

Answer: The solution set is A solid dot means that this point is included in the solution set.

Solve Graph the solution set on a number line. Write your answer using set-builder notation. Answer:

Solve Graph the solution set on a number line. Write your answer using interval notation. Original inequality Multiply each side by 2. Add –x to each side. Divide each side by – 3, reversing the inequality symbol.

Answer: The solution set is graphed below. and is

Solve Graph the solution set on a number line. Write your answer in interval notation. Answer:

ACT WARM-UP n If A ʘ B = 4 A − 3 B, then 9 ʘ 5 = ? n A) 11 B) 16 C) 21 D) 26 E) 31 n Substitute 9 for A and 5 for B. Evaluate the expression 4(9) − 3(5). The answer is C) 21.

A compound inequality consists of two inequalities joined by the word and or the word or. To solve a compound inequality, you must solve each part of the inequality. A compound inequality containing the word and is true if and only if both inequalities are true. A compound inequality containing the word or is true if one or more of the inequalities is true.

“And” Compound Inequalities The graph of a compound inequality containing and is the intersection of the solution sets of the two inequalities. The mathematical symbol for intersection is ∩. Compound inequalities involving the word and are called conjunctions.

Solution Notations The most common way of writing the solution x ≥ – 1 and x < 2 is – 1 ≤ x < 2. Both forms are read “x is greater than or equal to – 1 and less than 2”. Both inequality symbols for conjunctions are always < or ≤. In set-builder notation: {x | – 1 ≤ x < 2 } In interval notation: [– 1, 2 ), indicating that the solution set is the set of all numbers between – 1 and 2, including – 1, but not including 2.

Solve Graph the solution set on a number line. Method 1 Write the compound inequality using the word and. Then solve each inequality. and Method 2 Solve both parts at the same time by adding 2 to each part. Then divide each part by 3. 12 ≤

Graph the solution set for each inequality and find their intersection. y 4 Answer: Set Builder: {y | 4 ≤ y < 7} Interval Notation: [ 4, 7)

Solve Graph the solution set on a number line. Write your answer in set-builder notation. Answer:

“Or” Compound Inequalities The graph of a compound inequality containing or is the union of the solution sets of the two inequalities. The mathematical symbol for union is U. Compound inequalities involving the word or are called disjunctions.

Solution Notations The most common way of writing x ≤ 1 or x > 4 is by using the word “or” between the two inequalities. In set-builder notation: {x | x ≤ 1 or x > 4} In interval notation, the mathematical symbol for the union of the two sets is used and written as: (–∞, 1] U (4, +∞), indicating that all values less than and including 1 are part of the solution set. In addition, all values greater than 4, not including 4, are part of the solution set.

Solve each inequality separately. or Answer: The solution set is

Answer:

Solutions to Inequalities If you arrive at a false statement, such as 3 > 5, then the solution set for that inequality is the empty set { } or null set Ø. n If you arrive at a true statement such as 3 > – 1, then the solution set for that inequality is the set of all real numbers, written in set builder notation as {x | x Є R}, read as “ the set of all x ‘s such that x is an element of the real number system”. n

Inequality Phrases < is less than; is fewer than n > is greater than; is more than; or better than n ≤ is at most; is no more than; is less than or equal to n ≥ is at least; is no less than; is greater than or equal to n

Essential Question How are the rules for solving linear inequalities similar to those for solving linear equations, and how are they different? The addition and subtraction properties are the same, but if you multiply or divide both sides of an inequality by a negative number, the inequality symbol must be reversed.

Math Fact! n The cruise ship Queen Elizabeth 2 travels 40 feet on 1 gallon of fuel.