Equations and Functions ARITHMETIC METHOD FOR SOLVING EQUATIONS

Equations and Functions ARITHMETIC METHOD FOR SOLVING EQUATIONS

History

History of algebra Ø RHETORICAL ALGEBRA Ø 3 R D CENTURY Ø 6 T H -9 T H CENTURY

History

Rhetorical Algebra has been studied for many centuries. Babylonian, and ancient Chinese and Egyptian mathematicians proposed and solved problems in words, that is, using "rhetorical algebra". However, it was not until the 3 rd century that algebraic problems began to be considered in a form similar to those studied today.

3 rd century In the 3 rd century, the Greek mathematician Diophantus of Alexandria wrote his book Arithmetica. Of the 13 parts originally written, only six still survive, but they provide the earliest record of an attempt to use symbols to represent unknown quantities. Diophantus did not consider general methods in Arithmetica, but instead solved a large number of practical problems.

6 th-9 th century Several Indian mathematicians carried out important work in the field of algebra in the 6 th and 7 th centuries. Brahmagupta, who presented a general solution for a quadratic equation. The next major development in the history of algebra was the book al-Kitab al-muhtasar fi hisab al-jabr wa'l-muqabala ("Compendium on calculation by completion and balancing"), written by the Arabic mathematician Al. Khwarizmi in the 9 th century.

Mathematicians DIOPHANTUS HERON AL-KWARISMI BRAHMAGHUPTA

Diophantus

Diophantus of Alexandria (between 200 and 214 C) sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. Little is known about the life of Diophantus.

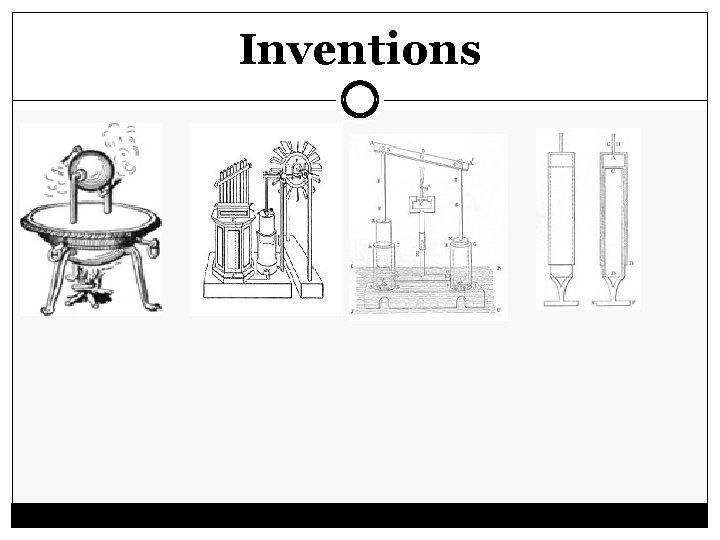
Heron of Alexandria (c. 10– 70 AD) was an ancient Greek mathematician who was a resident of a Roman province (Ptolemaic Egypt) he was also an engineer who was active in his native city of Alexandria. He is considered the greatest experimenter of antiquity and his work is representative of the Hellenistic scientific tradition. He was also an inventor. Some of his inventions is the Aeolipile, the wind-powered organ, the fireengine and the syringe.

Inventions

Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. The book Correctly Established Doctrine of Brahmagupta is one of the most famous books of this mathematician. It’s 25 chapters contain several unprecedented mathematical results. Brahmagupta was born in 598 CE (it is believed) in Bhinmal city in the state of Rajasthan of Northwest India

Al -kwarismi Abū ʿAbdallāh Muḥammad ibn Mūsā al-Khwārizmī (c. 780 – c. 850) was a Persian mathematician, astronomer and geographer, a scholar in the House of Wisdom in Baghdad. In Renaissance Europe he was considered the original inventor of algebra, although we now know that his work is based on older Indian or Greek sources. He revised Ptolemy's Geography and wrote on astronomy and astrology.

Algebra

Algebra EQUATIONS

Explanation Algebra provides a generalization of arithmetic by using symbols , usually letters to represent numbers. For example, it is true that : 2+3=3+2 We can generalize this statement and claim that: x+y=y+x is true, where x and y can be any number.

Arithmetic Equations WAY OF THINKING

Arithmetic Method For Solving Equations The Babylonians had a nice method of computing square roots that can be applied using only simple arithmetic operations. To find a rational approximation for the square root of an integer N, let’s suppose that k can be any number such that k 2 is less than N. Then k is slightly less than the square root of N, and so N/k is slightly greater than the square root of N. It follows that the average of these two numbers gives an even closer estimate

k+N/k K new=----2

Iterating this formula leads to k values that converge very rapidly on the square root of N. This formula is sometimes attributed to Heron of Alexandria, because he described it in his "Metrica. It's interesting to note that this formula can be seen as a special case of a more general formula for the roots of N, which arises from "ladder arithmetic" and we would call linear recurring sequences. The basic "ladder rule" for generating a sequence of integers to yield the square root of a number N is the recurrence formula

s[j] = 2 k s[j-1] + (N-k 2) s[j-2] where k is the largest integer such that k 2 is less than N. The ratio s[j+1]/s[j] approaches √(A+ N) as j goes to infinity. The sequence s[j] is closely related to the continued fraction for √N. This method does not converge as rapidly as the Babylonian formula, but it's often more convenient for finding the "best" rational approximations for denominators of a given size.

Example As an example, to find r = √ 7 we have N=7 and k=2, so the recurrence formula is simply s[j] = 4 s[j-1] + 3 s[j 2]. If we choose the initial values s[0]=0 and s[1]=1 we have the following sequence…. 0, 1, 4, 19, 88, 409, 1900, 8827, 41008, 190513, 885076, . . .

On this basis, the successive approximations and their squares are: r 2 (4/1) - 2 (19/4) - 2 (88/19) - 2 (409/88) – 2 (1900/409) - 2 (8827/1900) - 2 (41008/8827) - 2 (190513/41008) - 2 (885076/190513) - 2 4. 0 7. 5625 6. 9252. . . 7. 0104. . . 6. 99854. . . 7. 000201. . . 6. 9999719. . . 7. 00000390. . . 6. 999999457. . . etc.

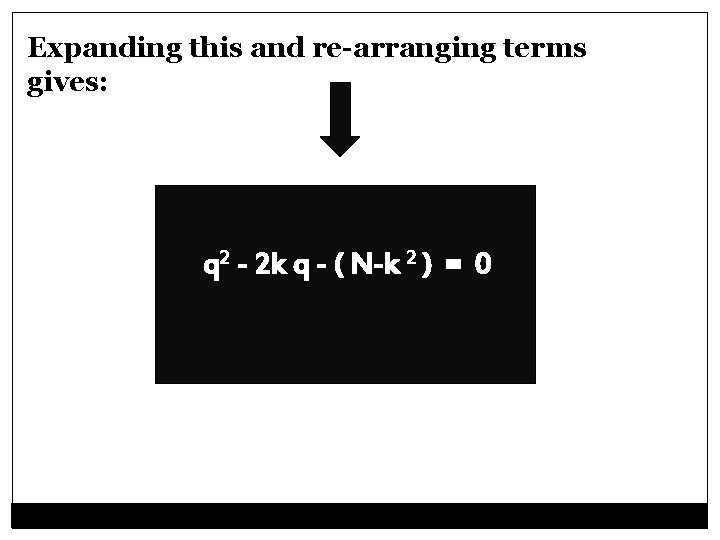
If we let q denote the ratio of successive terms q = s[j+1]/s[j], then the proposition is that q approaches √N+ k. In other words, we are trying to find the number q such that: (q - k) 2 = N

Expanding this and re-arranging terms gives: q 2 - 2 k q - ( N-k 2 ) = 0

It follows that the sequence of numbers s[0]=1, s[1]=q, s[2]=q 2. . , s[k]=qk, . . . satisfies the recurrence s[n] = 2 k s[n-1] + (N-k 2) s[n-2]

As can be seen by dividing through by s[n-2] and noting that q equals s[n 1]/s[n-2] and q 2 = s[n]/s[n-2]. Not surprisingly, then, if we apply this recurrence to arbitrary initial values s[0], s[1], the ratio of consecutive terms of the resulting sequence approaches q.

It's interesting that if we assume an EXACT rational (non-integer) value for √A and exercise the algorithm in reverse, we generate an infinite sequence of positive integers whose magnitudes are strictly decreasing, which of course is impossible.

Maria Deliveri 3 rd General Lyceum of Karditsa