Equaes de 1 grau Acadmicas Eliane Moreira da

Equações de 1° grau Acadêmicas: Eliane Moreira da Silva Lisiane Milan Selong

Objetivo geral da unidade: Estimular no aluno a curiosidade, iniciativa, exploração e consciência de seu desenvolvimento lógico e aprendizagem, levando o a compreensão de conceitos, procedimentos e estratégias a partir das experiências acumuladas no seu dia a dia. Além disso, propiciar um ambiente capaz de promover a interação e a aprendizagem matemática.

Objetivos específicos: • Construir com o aluno o conceito de equação, através de situações problema; • Demonstrar através da história a origem das equações; • Diferenciar sentença aberta de sentença fechada; • Exemplificar o conceito de equação utilizando material concreto; • Distinguir expressão algébrica de equação;

• Determinar o conjunto solução de uma equação dentro de um determinado conjunto universo; • Reconhecer como equação do 1° grau com uma incógnita toda equação equivalente a ax=b, onde a, b Є Q e a≠ 0; • Aplicar os princípios de equivalência para obter equações equivalentes e mais simples na forma ax=b; • Escrever o conjunto solução da equação de acordo com o conjunto universo dado; • Traduzir uma sentença expressa em linguagem corrente em uma sentença matemática;

• Identificar o que é dado e o que é pedido no problema; • Analisar o resultado e dar a resposta conveniente ao problema;

Metodologia: Aulas expositivas e dialogadas com a utilização de quadro e giz, situações problemas, resolução de exercícios, utilização de material concreto e software educacional.

Avaliação: A avaliação será feita pela observação do desempenho do aluno tanto individualmente quanto em grupo durante a realização das atividades propostas, assiduidade, interesse, trabalho em dupla e avaliação escrita.

Conteúdos:

1 -Introdução à Álgebra: Seqüências Um jardineiro faz canteiros com mudas de rosa e mudas de margarida, arrumando em grupos como os modelos abaixo. No seu caderno, copie a tabela a seguir e relacione o número de mudas de rosa que ele planta em cada grupo com o número de mudas de margarida. ROSA MARGARIDA 1 4 2 ? ? ?

2 -História das equações: O enigma de Diofante Até aquela época, os matemáticos gregos preferiam estudar Geometria. Apenas Diofante se dedicou à Álgebra. A História não guardou muitos da dos sobre a vida de Diofante. Tudo o que sabemos dele estava numa dedica tória gravada em seu túmulo — com toda a certeza, escrita por Hipatia:

“Caminhante! Aqui fo ramsepultados os res tos de Diofante. E os números podem mos trar — oh, milagre — quão longa foi a sua vida”, x cuja sexta parte consti tuiu sua formosa infância. x/6 E mais um duodécimo pedaço de sua vida havia transcorrido quan do de pêlos se cobriu o seu rosto. x/12 E a sétima parte de sua existência transcorreu em um matrimônio sem filhos. x/7 Passou se um qüinqüênio mais e deixou o muito feliz o nascimen to de seu 5 primeiro filho, que entregou à terra seu corpo, sua formosa vida, que durou somente a metade da de seu pai. E x/2 com profundo pesar desceu à sepultura, tendo sobrevivido apenas 4 quatro anos ao descenso de seu filho.

Hoje nós sabemos decifrar esta dedicatória através de uma equação: Fazemos os cálculos:

Agora podemos resolver todo o enigma, substituindo x por 84: “Caminhante! Aqui foram sepultados os res tos de Diofante. E os números podem mos trar — oh, milagre — quão longa foi a sua vida”, x=84 cuja sexta parte consti tuiu sua formosa infância. x/6=84/6=14 E mais um duodécimo pedaço de sua vida havia transcorrido quan do x/12=84/12=7 de pêlos se cobriu o seu rosto. E a sétima parte de sua existência transcorreu em um matrimônio sem filhos. x/7=84/7=12 Passou se um qüinqüênio mais e deixou o muito feliz o nascimen tode seu primeiro filho, 5 que entregou à terra seu corpo, sua formosa vida, que durou somente a metade da de seu pai. x/2=84/2=42 E com profundo pesar desceu à sepultura, tendo sobrevivido apenas quatro anos ao descenso de seu filho. 4 Diga me: Quantos anos viveu Diofante quando lhe chegou a morte? ”

Assim, ficamos sabendo que Diofante morreu aos 84 anos. Quatro anos antes presenciou a morte do filho, que tinha 42 anos: ½ • 84 = 42 Diofante foi pai, portanto, com 38 anos e casou se aos 21 anos: 80 42 = 38 38 5 12 = 21 Os matemáticos da época de Hipatia e Diofante não conheciam as equações. Apenas os mais brilhantes eram capazes de resolver problemas desafio como este.

Matemáticos de várias partes do mundo adotaram a regra do falso dos egípcios. Veja este famoso quebra cabeça hindu do século VII: “Um colar se rompeu quando brincavam dois namorados. . . Uma fileira de pérolas escapou. . . A sexta parte ao solo caiu. . . A quinta parte na cama ficou. . . Um terço pela jovem se salvou. . . A décima parte o namorado recolheu. . . E com seis pérolas o colar ficou. . . Diga-me, leitor, quantas pérolas tinha o colar dos namorados? ” Um estudante hindu dessa época resolvia o problema através da regra do falso; o montão representava a quantidade de pérolas do colar.

Escolhia um valor falso: Valor falso = 60 Montava uma regra de três simples: VALOR FALSO VALOR VERDADEIRO 60 Montão 12 6

Descobria assim que o colar dos namorados tinha 30 pérolas. Vamos conferir o resultado resolvendo o problema através de uma equação:

3 - De símbolos a palavras; de palavras a símbolos: Quando escrevemos uma expressão algébrica, por exemplo: x l podemos imaginar uma frase que seja representada por essa expressão: "Pedro tem um livro a menos que Carol. " Se x representa o número de livros que Carol possui, x — l representa a quantidade de livros de Pedro. Podemos pensar numa outra interpretação: "Se x representa um número inteiro, x — l representa o antecessor desse número. " Outra expressão algébrica: 2 y l pode representar a frase:

"O dobro de um número menos l" ou ainda: "Subtraindo l ano do dobro da idade de Sandro, obtemos a idade de Ana. " Se y representa a idade de Sandro, 2 y — l representa a idade de Ana. Também podemos fazer o inverso: dada uma frase, representá la por meio de uma expressão algébrica. Veja: • um número somado com 5: b + 5; • a diferença entre um número e 10: y — 10; • o dobro de um número: 2 • x ou 2 x; • se Pedro é l ano mais velho que Manuel e a idade de Manuel é representada por a, representamos a idade de Pedro por a + 1.

4 Sentenças matemáticas fechadas e sentenças matemáticas abertas:

As sentenças matemáticas A maneira como a Matemática se desenvolveu, com a descoberta de relações entre M medidas, por exemplo, fez com que os matemáticos se vissem obrigados a usar símbolos que viessem a simplificar a escrita das sentenças matemáticas relativas a tais relações. Os símbolos que surgiram espontaneamente foram as letras dos diversos alfabetos mais co nhecidos assim como sinais específicos indicando operações e relações. Assim, para afirmar que a área do retângulo é o produto das duas dimensões, con vencionou se estabelecer a fórmula que vocês já conhecem, ou seja: S =b • h Onde: S, b e h são símbolos que representam, respectivamente, a medida da área do retângulo, a medida da base e a medida da altura. Temos, nesta fórmula, uma sentença matemática escrita simbolicamente; é uma sentença porque é a expressão de um pensamento completo, ou seja, traduz uma idéia formando sentido completo. Assim, toda relação entre estes matemáticos passou a expressar se por meio de símbolos, ou seja, por meio de sentenças matemáticas escritas na linguagem simbólica.

5 -Equação: Denomina se equação toda sentença matemática aberta expressa por uma igualdade que tem pelo menos um número desconhecido representado por uma letra. Como toda equação é uma igualdade, temos: x + 2 = 6→ 2° membro da equação ↓ 1° membro da equação x – y = 10→ 2° membro da equação ↓ 1° membro da equação

6 -Variável ou incógnita de uma equação: Observe: 5 x + 2 2 x + 3 = 7 Qual a diferença entre as duas sentenças matemáticas? Que nome se dá ao “x” nessas duas sentenças? • 5 x + 2→ é uma expressão algébrica, nesse caso o “x” recebe o nome de variável; • 2 x + 3 = 7→é uma equação algébrica (é expressa por uma igualdade), nesse caso o “x” recebe o nome de incógnita;

7 -Conjunto universo e conjunto solução de uma equação: Representação: U = conjunto universo S = conjunto solução (conjunto verdade) Recordemos os conjuntos numéricos já estudados, para posterior aplicação: N = {números naturais} = { 0, 1, 2, 3, 4, 5, . . . } Z = {números inteiros} = {. . . , 3, 2, 1, 0, 1, 2, 3, . . . } Q = { números racionais} = {. . . , 2, . . . , 1, . . . , ½, . . . , 0, . . . , ⅓, . . . , 1, . . . } Veremos, por meio de exercícios práticos, o significado de conjunto universo e conjunto solução de uma equação.

Qual o elemento do conjunto A = {0, 1, 2, 3, 4} que torna verdadeira a equação x + 1 = 3? Resposta: O elemento é 2, pois (2) + 1 = 3 Significado: O conjunto A = {0, 1, 2, 3, 4} é denominado conjunto universo da equação. O conjunto {2} é denominado conjunto solução da equação (relativo aquele conjunto universo). Em síntese: Equação: x + 1 = 3 U = {0, 1, 2, 3, 4} S = {2}

Conjunto universo é o conjunto formado por todos os valores pelos quais a variável pode ser substituída. Conjunto solução é o conjunto constituído por todos os elementos do conjunto universo dado, que tornem verdadeira a equação.

8 -Equação do 1° grau com uma incógnita: 1°) x = 11 2°) 3 y = 21 3°) 10 t = 2 4°) 6 p = 1 5°) 5 m = 0 6°) 7 x – 1 = 6 x + 11 7°) y + ⅔y = 120 → A incógnita é x →A incógnita é y → A incógnita é t →A incógnita é p → A incógnita é m → A incógnita é x → A incógnita é y Como reconhecer, então, se uma equação é do 1° grau com uma incógnita? Toda equação que, reduzida à sua forma mais simples, assume a forma ax = b, em que x representa a incógnita e b são números racionais, com a ≠ 0, é denominada equação do 1° grau com uma incógnita. Os números a e b são denominados coeficientes da equação.

9 - Resolvendo uma equação do 1° grau com uma incógnita: Resolver a equação 3 x + 1 = 37 sendo U = Q. Aplicando o princípio aditivo, vamos adicionar (-1) aos dois membros da equação, isolando o termo que tem a incógnita x no 1° membro: 3 x + 1 = 37 3 x + 1 + (-1) = 37 + (-1) 3 x +1 -1 = 37 – 1 3 x = 36 Aplicando o princípio multiplicativo, vamos multiplicar os dois membros da equação por ⅓, descobrindo assim o valor do número x.

3 x. (⅓) = 36. (⅓) x = 12 Como 12 Є Q, temos S = {12} De forma prática: 3 x + 1 = 37 3 x = 37 – 1 → aplicamos o princípio aditivo 3 x = 36 ÷ 3 → aplicamos o princípio multiplicativo x = 12 Como 12 Є Q, temos S = {12}

10 -Explorando a idéia de equilíbrio e resolvendo equações de 1° grau com uma incógnita: Vamos agora trabalhar com mais um modo de resolver equações. A igualdade traduz uma idéia de equilíbrio. Equilíbrio faz a gente se lembrar de uma balança de dois pratos. Assim, uma equação (que é uma igualdade) pode ser vista como uma balança de dois pratos em equilíbrio.

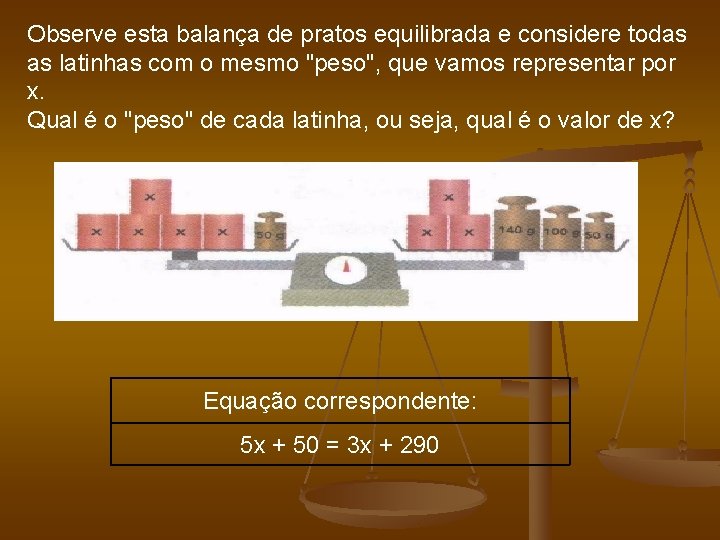
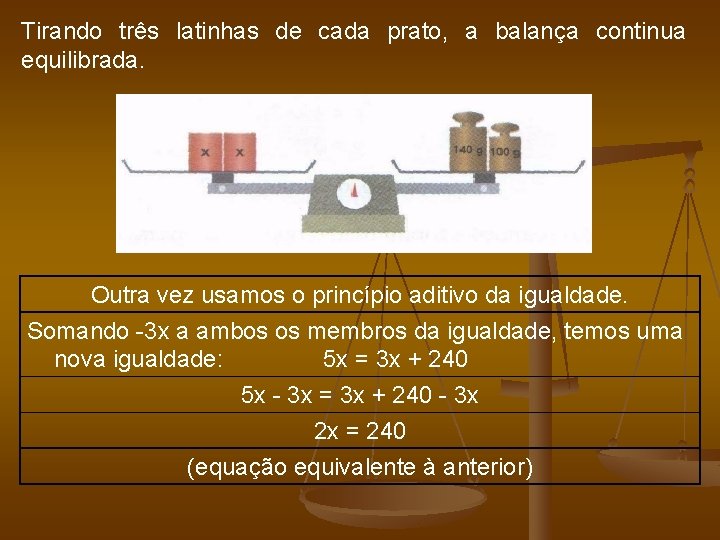
Observe esta balança de pratos equilibrada e considere todas as latinhas com o mesmo "peso", que vamos representar por x. Qual é o "peso" de cada latinha, ou seja, qual é o valor de x? Equação correspondente: 5 x + 50 = 3 x + 290

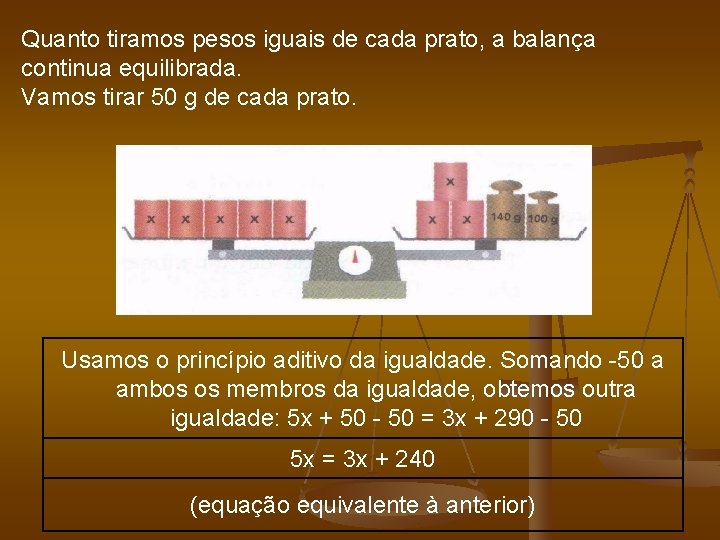
Quanto tiramos pesos iguais de cada prato, a balança continua equilibrada. Vamos tirar 50 g de cada prato. Usamos o princípio aditivo da igualdade. Somando 50 a ambos os membros da igualdade, obtemos outra igualdade: 5 x + 50 = 3 x + 290 50 5 x = 3 x + 240 (equação equivalente à anterior)

Tirando três latinhas de cada prato, a balança continua equilibrada. Outra vez usamos o princípio aditivo da igualdade. Somando 3 x a ambos os membros da igualdade, temos uma nova igualdade: 5 x = 3 x + 240 5 x 3 x = 3 x + 240 3 x 2 x = 240 (equação equivalente à anterior)

Se duas latinhas de mesmo "peso", juntas, "pesam" 240 g, cada uma "pesa" 240 : 2 = 120 g. Assim o "peso" de cada latinha é de 120 g. Se 2 x = 240, pela operação inversa obtemos x: x = 240 : 2 x = 120

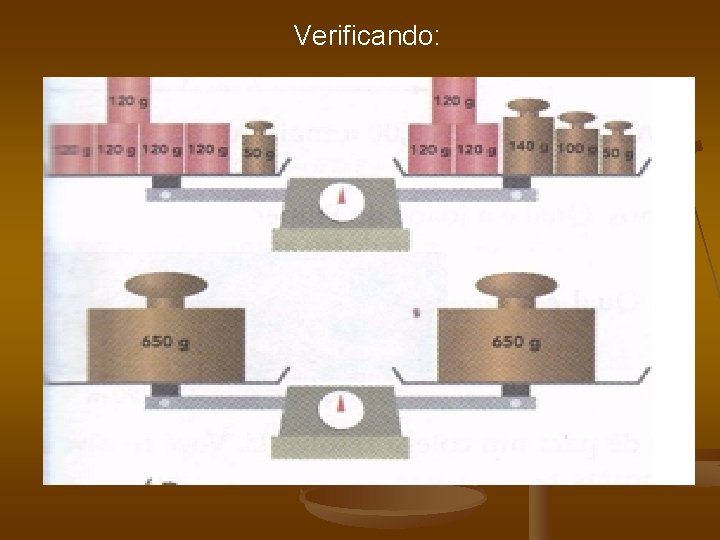
Verificando:

Verificando: 5 x + 50 = 3 x + 290 5. 120 + 50 = 3. 120 + 290 600 + 50 = 360 + 290 650 = 650 (está correto)

11 - Usando as equações para resolver problemas: Veja algumas dicas abaixo. Elas serão importantes para equacionar e resolver as situações-problema: • Leia com atenção a situação dada verificando o que se conhece e o que se vai determinar; • Represente um valor desconhecido por uma letra; • Escreva uma equação envolvendo essa letra, seguindo as informações da situação; • Resolva a equação obtendo o valor da letra; • Faça a verificação conferindo se acertou; • Escreva a resposta.