Epipolar Geometry Essential Matrix LonguetHiggins 1981 Fundamental Matrix

Epipolar Geometry • Essential Matrix (Longuet-Higgins 1981) • Fundamental Matrix (Faugeras 1992) • F and Homographies

ESSENTIAL MATRIX

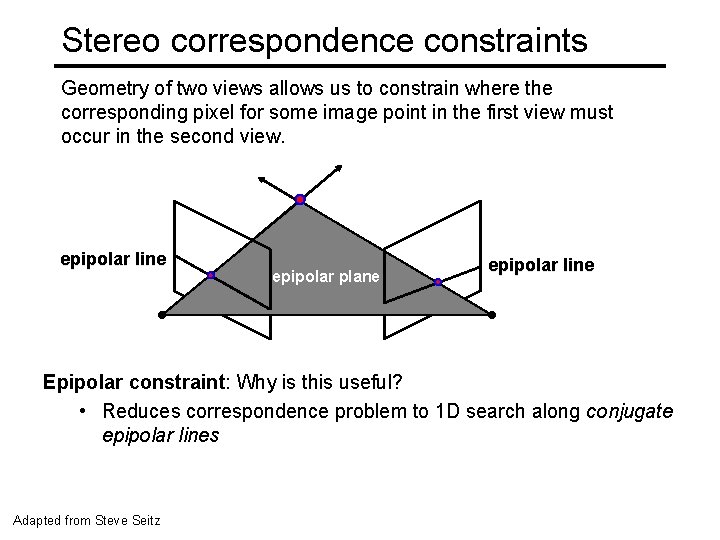
Stereo correspondence constraints Geometry of two views allows us to constrain where the corresponding pixel for some image point in the first view must occur in the second view. epipolar line epipolar plane epipolar line Epipolar constraint: Why is this useful? • Reduces correspondence problem to 1 D search along conjugate epipolar lines Adapted from Steve Seitz

Epipolar geometry: terms Baseline: line joining the camera centers Epipole: point of intersection of baseline with the image plane Epipolar plane: plane containing baseline and world point Epipolar line: intersection of epipolar plane with the image plane All epipolar lines intersect at the epipole An epipolar plane intersects the left and right image planes in epipolar lines

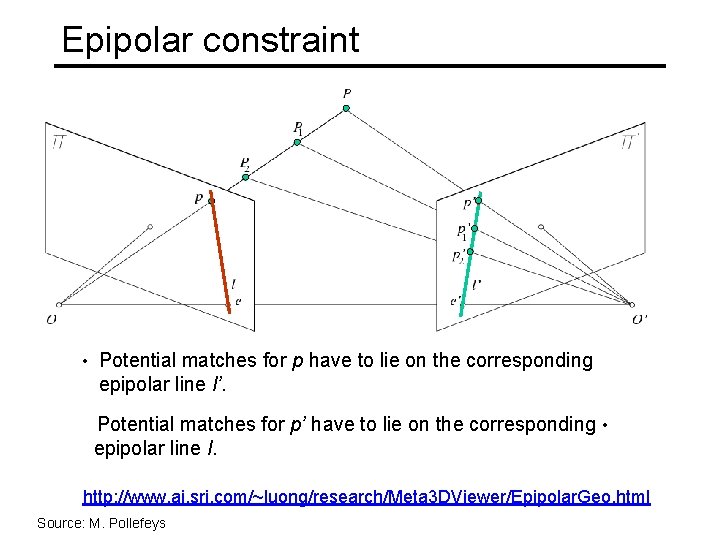
Epipolar constraint • Potential matches for p have to lie on the corresponding epipolar line l’. Potential matches for p’ have to lie on the corresponding • epipolar line l. http: //www. ai. sri. com/~luong/research/Meta 3 DViewer/Epipolar. Geo. html Source: M. Pollefeys

Example

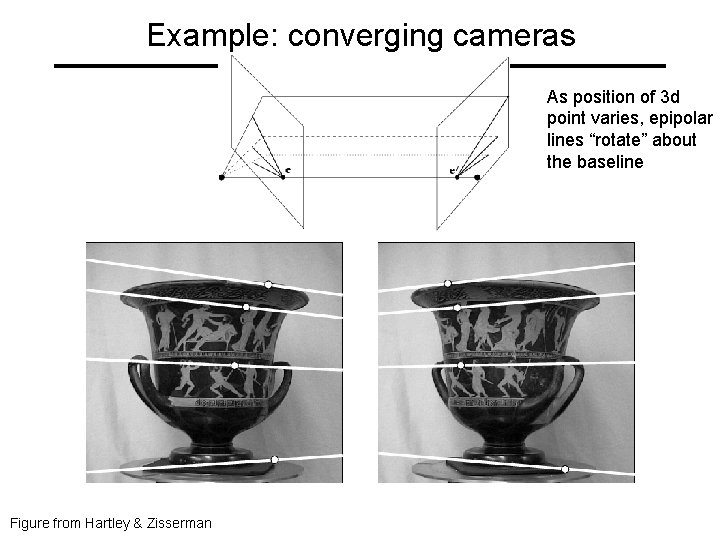
Example: converging cameras As position of 3 d point varies, epipolar lines “rotate” about the baseline Figure from Hartley & Zisserman

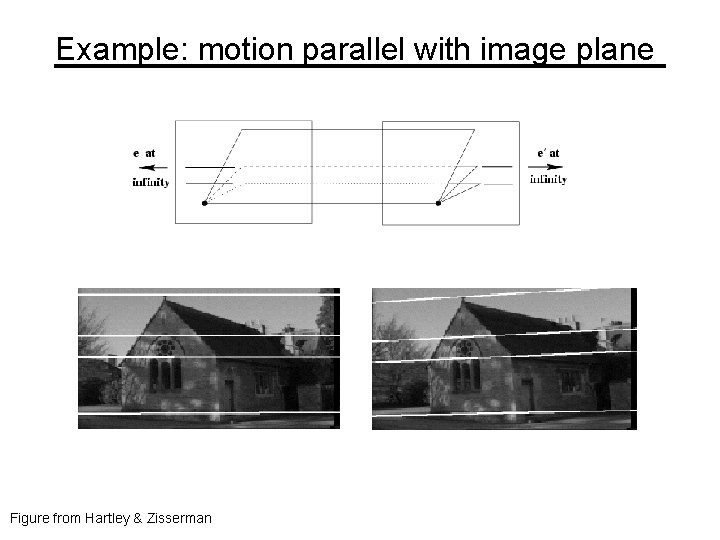
Example: motion parallel with image plane Figure from Hartley & Zisserman

Example: forward motion e’ e Epipole has same coordinates in both images. Points move along lines radiating from e: “Focus of expansion” Figure from Hartley & Zisserman

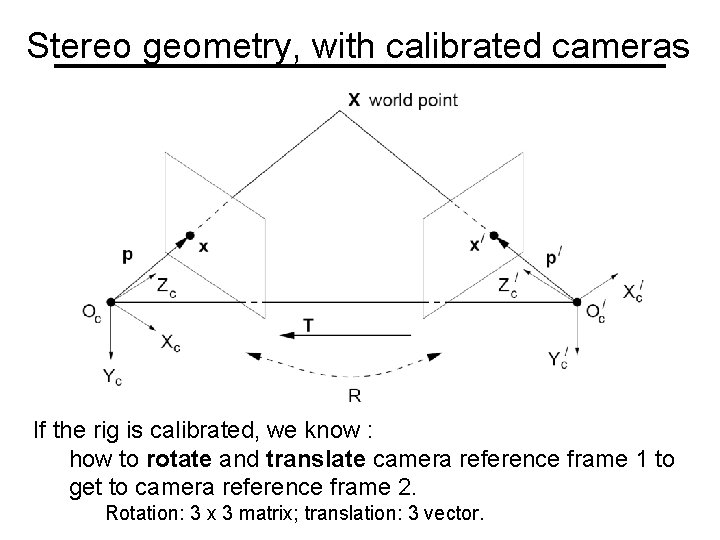
Stereo geometry, with calibrated cameras If the rig is calibrated, we know : how to rotate and translate camera reference frame 1 to get to camera reference frame 2. Rotation: 3 x 3 matrix; translation: 3 vector.

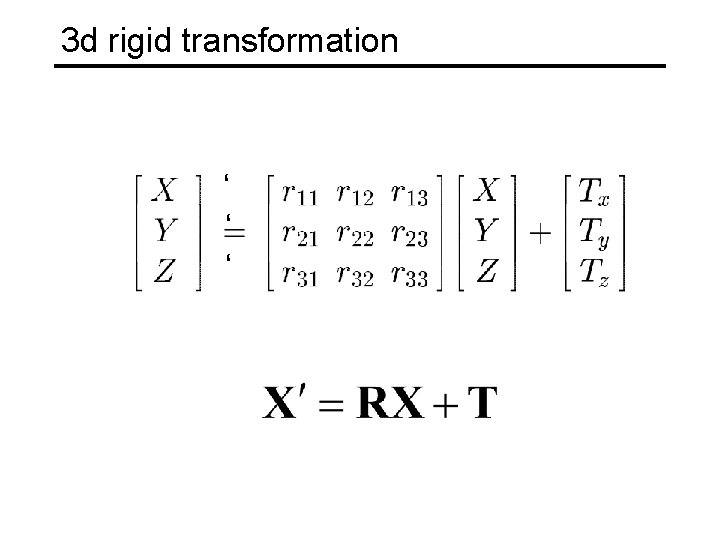
3 d rigid transformation ‘ ‘ ‘

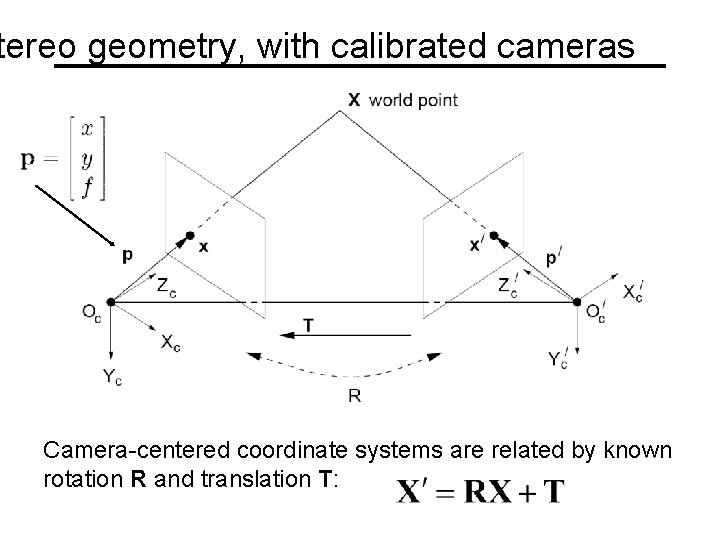
tereo geometry, with calibrated cameras Camera-centered coordinate systems are related by known rotation R and translation T:

Cross product Vector cross product takes two vectors and returns a third vector that’s perpendicular to both inputs. So here, c is perpendicular to both a and b, which means the dot product = 0.

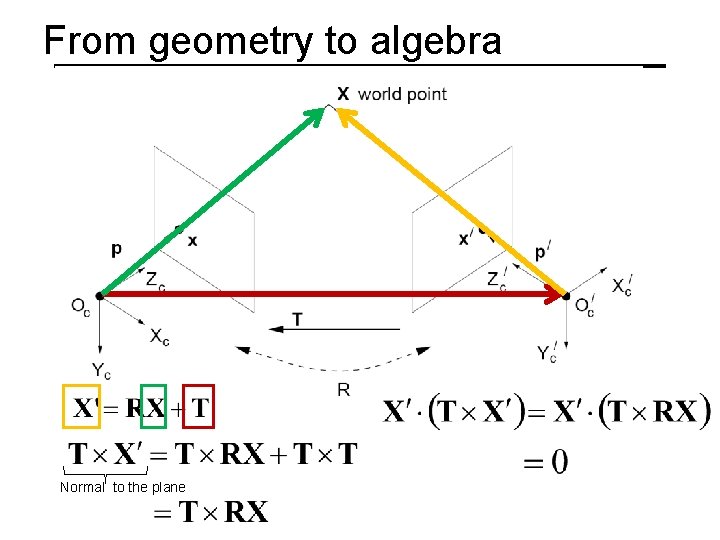
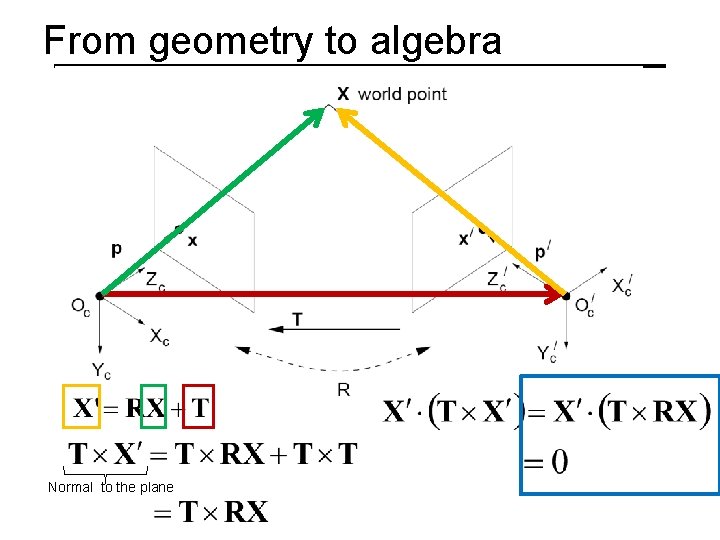
From geometry to algebra Normal to the plane

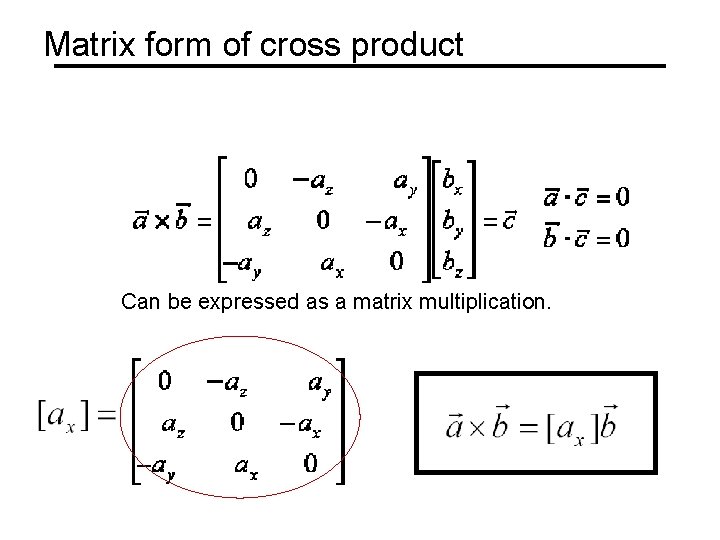
Matrix form of cross product Can be expressed as a matrix multiplication.

From geometry to algebra Normal to the plane

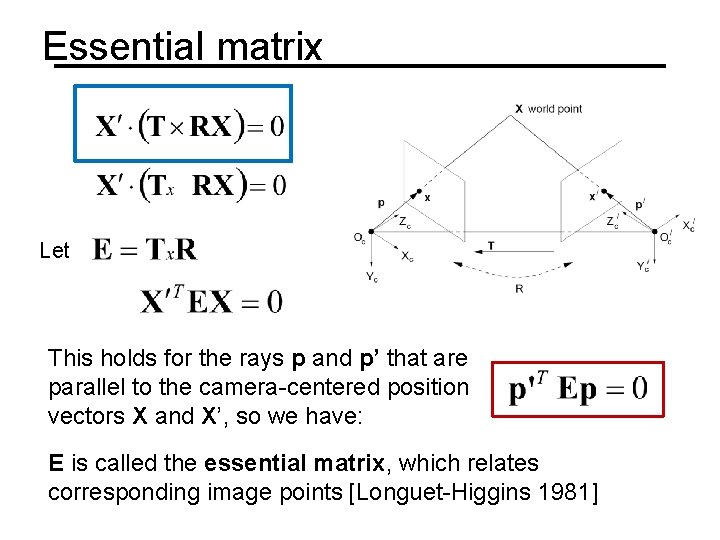
Essential matrix Let This holds for the rays p and p’ that are parallel to the camera-centered position vectors X and X’, so we have: E is called the essential matrix, which relates corresponding image points [Longuet-Higgins 1981]

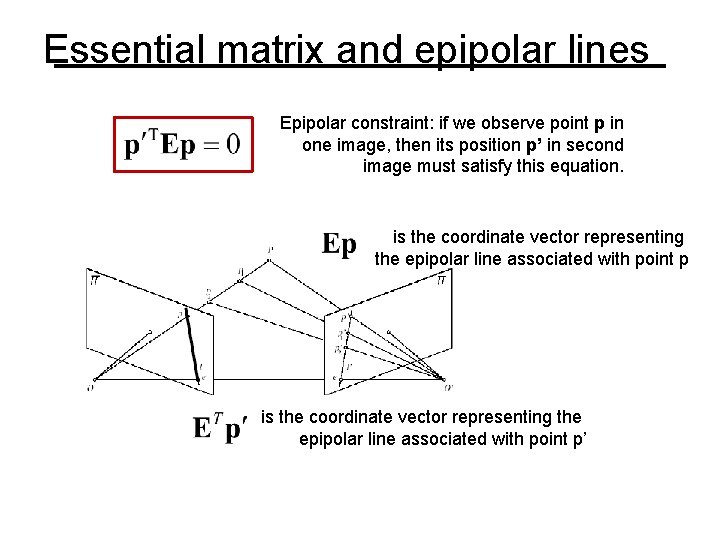
Essential matrix and epipolar lines Epipolar constraint: if we observe point p in one image, then its position p’ in second image must satisfy this equation. is the coordinate vector representing the epipolar line associated with point p’

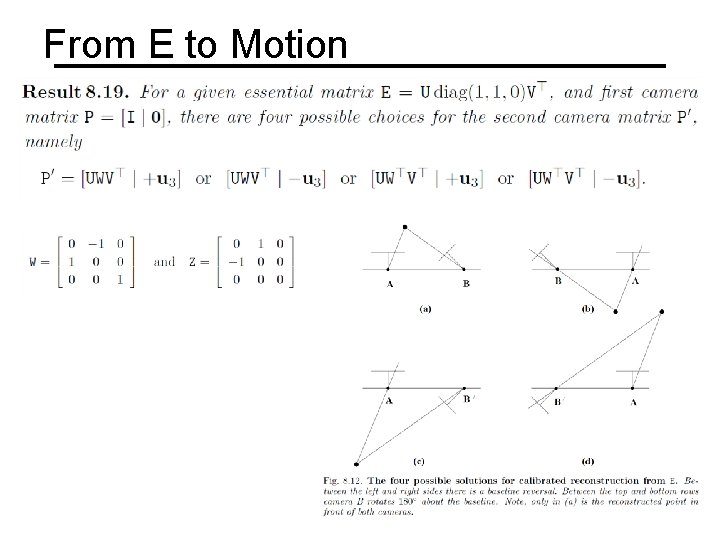
Essential matrix: properties Relates image of corresponding points in both cameras, given rotation and translation Assuming intrinsic parameters are known E is a rank 2 matrix with two equal eigvenvalues Given E, the camera projection matrix can be computed using SVD factorization. There are four possible solutions

From E to Motion

FUNDAMENTAL MATRIX

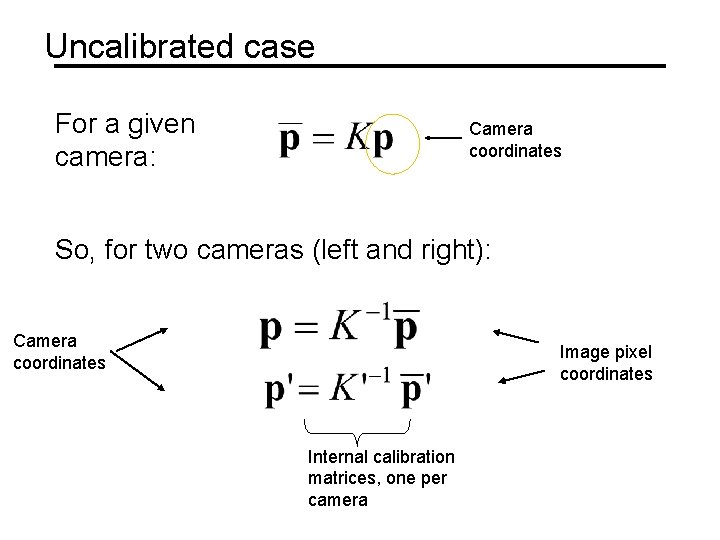
Uncalibrated case For a given camera: Camera coordinates So, for two cameras (left and right): Camera coordinates Image pixel coordinates Internal calibration matrices, one per camera

Uncalibrated case: fundamental matrix From before, the essential matrix E. Fundamental matrix

Fundamental matrix Relates pixel coordinates in the two views More general form than essential matrix: we remove need to know intrinsic parameters If we estimate fundamental matrix from correspondences in pixel coordinates, can reconstruct epipolar geometry without intrinsic or extrinsic parameters

Computing F from correspondences Cameras are uncalibrated: we don’t know E or left or right K matrices Estimate F from 8+ point correspondences.

Computing F from correspondences Each point correspondence generates one constraint on F Collect n of these constraints Solve for f , vector of parameters.

F AND HOMOGRAPHIES

F decomposition Given F, we want to decompose to left and right projection matrices. Because reconstruction is up to global projective transformation we can set the left camera projection matrix to [I; 0]. Since p’^t. Fp=0 for every pair of points, there is one point e’ s. t. e’^t. Fp=0 for every p -> e’ is in the null space of F. e’ is the epipole and all epipolar lines go through it. From the epipolar constraint (shown for the essential matrix) we have that So, we have M_1=[I; 0] and M_2 = [H, e’] Where H is a homography

The rank-4 of homographies

The canonical homography Choose some line l’ going through p’ then: l’^T p’ = 0 And from the epipolar constraint we have: p’^TFp = 0 Combining the two we have that p’ is on the intersection of the two lines: P’ =~ [l’]_x Fp And we have a homography equation: p’ =~ [l’]_x Fp =Hp In particular, lets choose l’ =~ e’, which is guaranteed not to coincide with the epipolar lines (e’Te’ !=0) and have that H = [e’]_x. F is a homography that is called the canonical homography matrix

Relationship between F and H What is the relationship between homography and fundamental matrix? Let’s choose some homography, then we have: (Hp)^TFp = 0 and this is true for every point p. So we have that Fp =~ [e’]_x Hp, because they both describe the epipolar line s. t. p’^TFp and p’^T [e’]_x Hp=0 Geometric interpretation: The points Hp, p’ and e’ are all on the same line (the epipolar line) And this can be written as: p’^T[e]_x. Hp=0