Epidemic Dissemination Efficient Broadcasting in PeertoPeer Systems Laurent

Epidemic Dissemination & Efficient Broadcasting in Peer-to-Peer Systems Laurent Massoulié Thomson, Paris Research Lab Based on joint work with: Bruce Hajek, Sujay Sanghavi, Andy Twigg, Christos Gkantsidis and Pablo Rodriguez

Context l P 2 P systems for live streaming & Video-on-Demand – PPLive, Sopcast, TVUPlay, Joost, Kontiki… l Internet hosts form overlay network – Data exchanges between overlay neighbours – Aim: real time playback at all receivers l 2 Soon the main channel for multimedia diffusion?

Diffusion of Code Red Virus 3

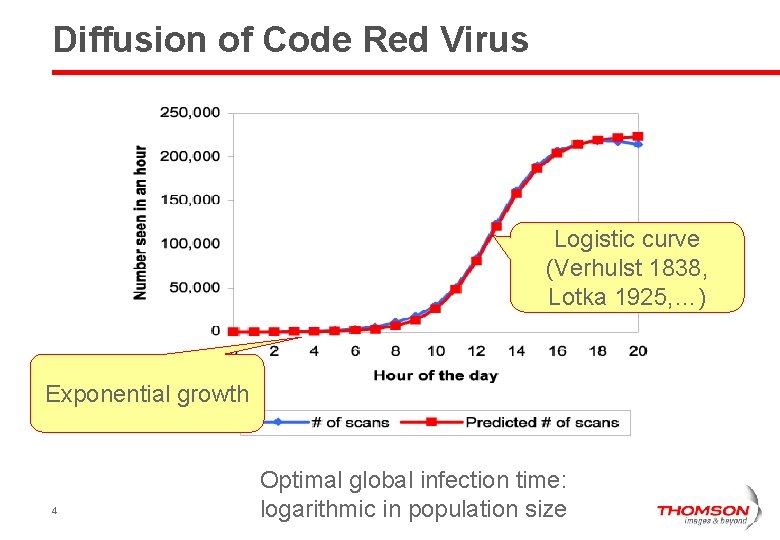
Diffusion of Code Red Virus Logistic curve (Verhulst 1838, Lotka 1925, …) Exponential growth 4 Optimal global infection time: logarithmic in population size

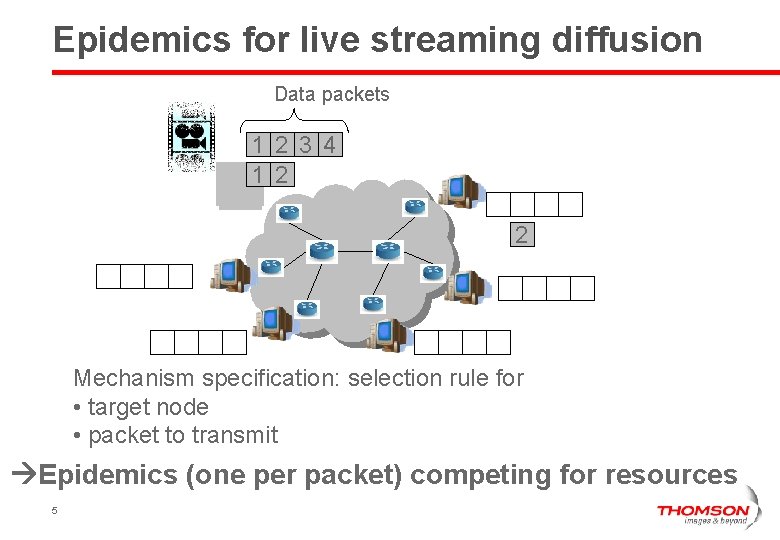
Epidemics for live streaming diffusion Data packets 1 2 3 4 1 2 2 Mechanism specification: selection rule for • target node • packet to transmit Epidemics (one per packet) competing for resources 5

Problem statement l Currently deployed systems rely on epidemic approach l Appeal of simple & decentralised schemes – Large user populations (103 – 106) – High churn (nodes join and leave) “Cost of decentralisation? i. e. , can epidemics make efficient use of communication resources? Metrics: rate and delay 6

Outline l Delay-optimal schemes [S. Sanghavi, B. Hajek, LM] l Rate-optimal schemes [LM, C. Gkantsidis, P. Rodriguez and A. Twigg] l Outlook 7

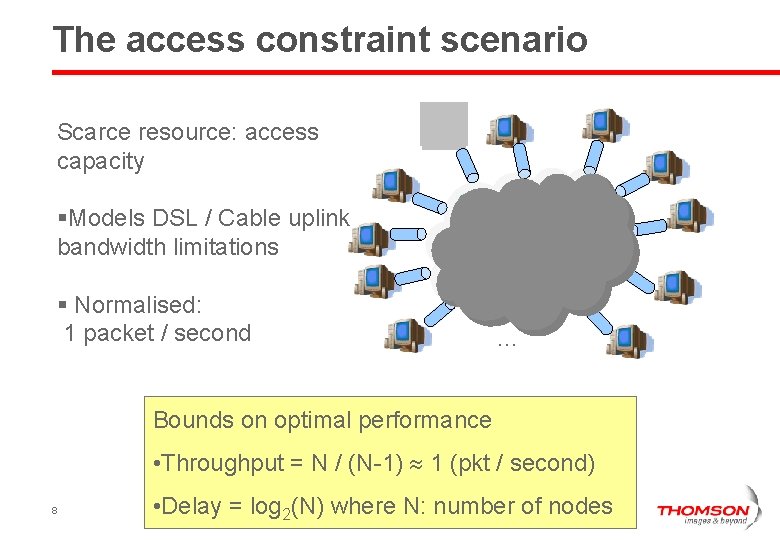
The access constraint scenario Scarce resource: access capacity §Models DSL / Cable uplink bandwidth limitations § Normalised: 1 packet / second … Bounds on optimal performance • Throughput = N / (N-1) 1 (pkt / second) 8 • Delay = log 2(N) where N: number of nodes

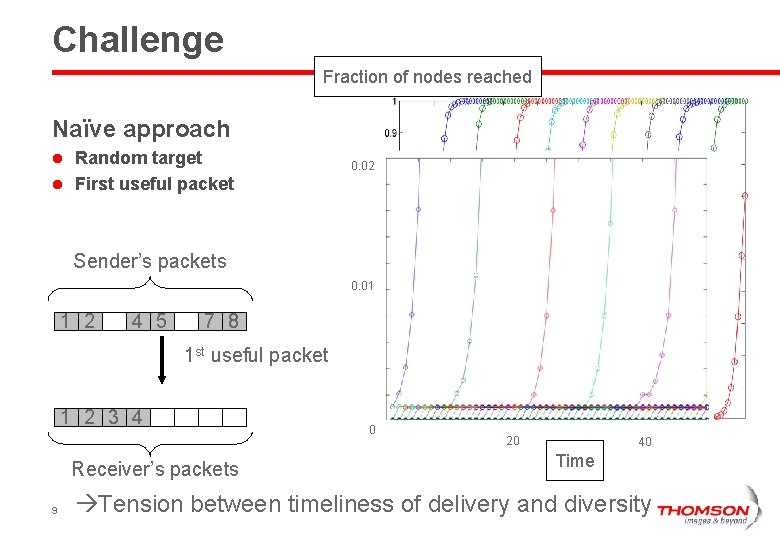
Challenge Fraction of nodes reached Naïve approach Random target l First useful packet l 0. 02 1 2 3 Sender’s packets 0. 01 1 2 4 5 7 8 1 st useful packet 1 2 3 4 Receiver’s packets 9 0 20 40 Time Tension between timeliness of delivery and diversity

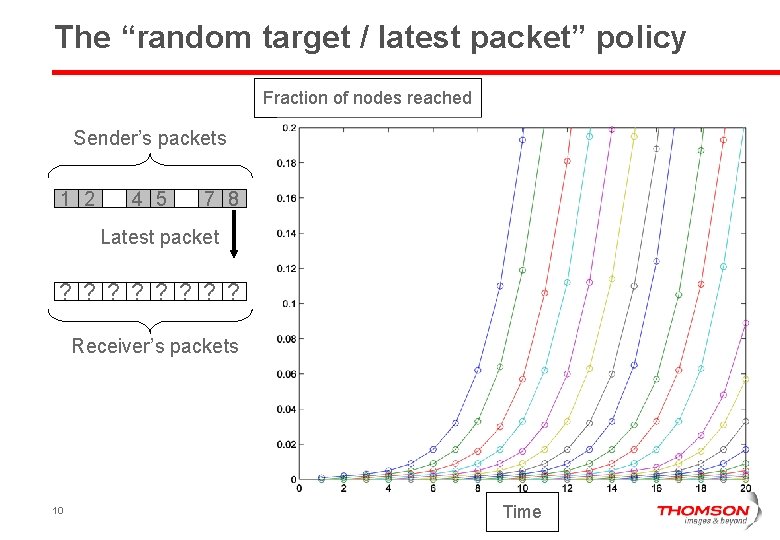
The “random target / latest packet” policy Fraction of nodes reached Sender’s packets 1 2 4 5 7 8 Latest packet ? ? ? ? Receiver’s packets 10 Time

The “random target / latest packet” policy Main result: Each node receives each packet w. p. 1 -1/e 63% with optimal delay ( less than log 2(N) ), Independently for distinct packets. Diffusion at rate 63% of optimal and with optimal delay feasible (Do source coding at source over consecutive data windows) 11

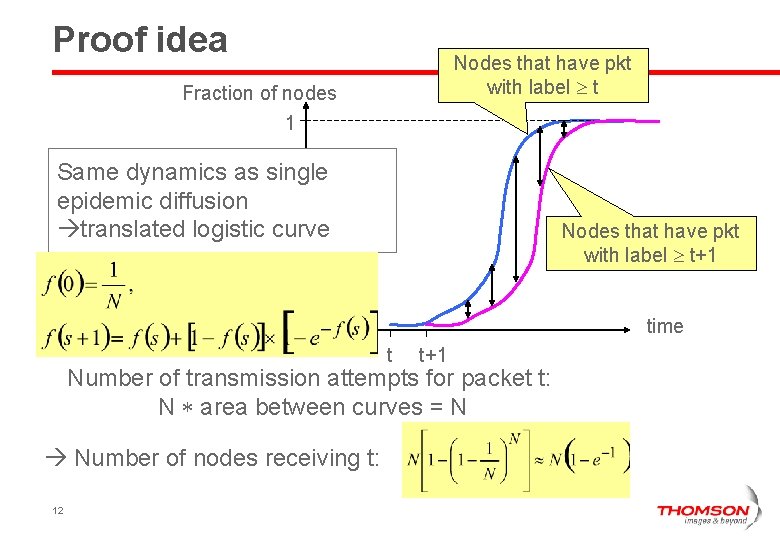
Proof idea Nodes that have pkt with label t Fraction of nodes 1 Same dynamics as single epidemic diffusion translated logistic curve Nodes that have pkt with label t+1 time t t+1 Number of transmission attempts for packet t: N area between curves = N Number of nodes receiving t: 12

Outline l Delay-optimal schemes [S. Sanghavi, B. Hajek, LM] l Rate-optimal schemes [LM, C. Gkantsidis, P. Rodriguez and A. Twigg] l Outlook 13

Access constraints scenario l. Network assumptions: – access capacities, ci – Everyone can send to everyone (complete communication graph) l. Statistical assumptions: – source creates fresh packets at instants of Poisson process with rate λ – Packet transmission time from node i: Exponential r. v. with mean 1/ci Optimal broadcast rate: 14

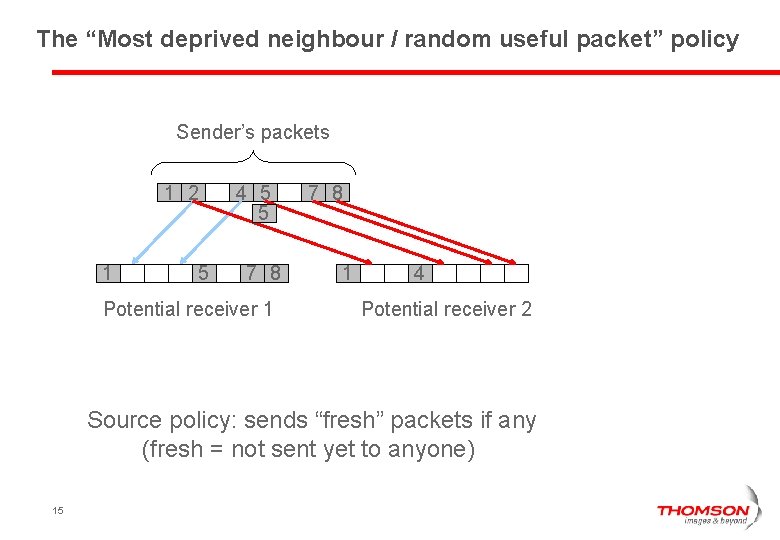
The “Most deprived neighbour / random useful packet” policy Sender’s packets 1 2 1 5 4 5 5 7 8 Potential receiver 1 7 8 1 4 Potential receiver 2 Source policy: sends “fresh” packets if any (fresh = not sent yet to anyone) 15

Main result Provided λ < λ*, Markov process describing system state is ergodic. l Hence all packets are received at all nodes after time bounded in probability l Proof: identifies “workload” as Lyapunov function for fluid dynamics of Markov process Open questions: l Magnitude of delays (simulations suggest logarithmic) l Extension to general, not complete graphs 16

Extension to limited neighborhoods Each node maintains shortlist of neighbours l Sends to most deprived from neighbour set l Periodically adds randomly chosen neighour, and dumps least deprived Neighbourhood size stays fixed l Ergodicity result still holds: fluid dynamics unchanged Q: impact of neighborhood size? 17

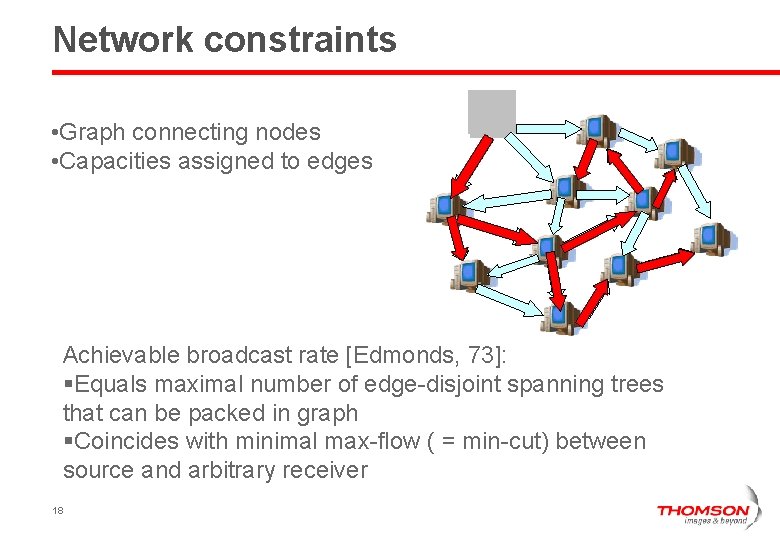
Network constraints • Graph connecting nodes • Capacities assigned to edges Achievable broadcast rate [Edmonds, 73]: §Equals maximal number of edge-disjoint spanning trees that can be packed in graph §Coincides with minimal max-flow ( = min-cut) between source and arbitrary receiver 18

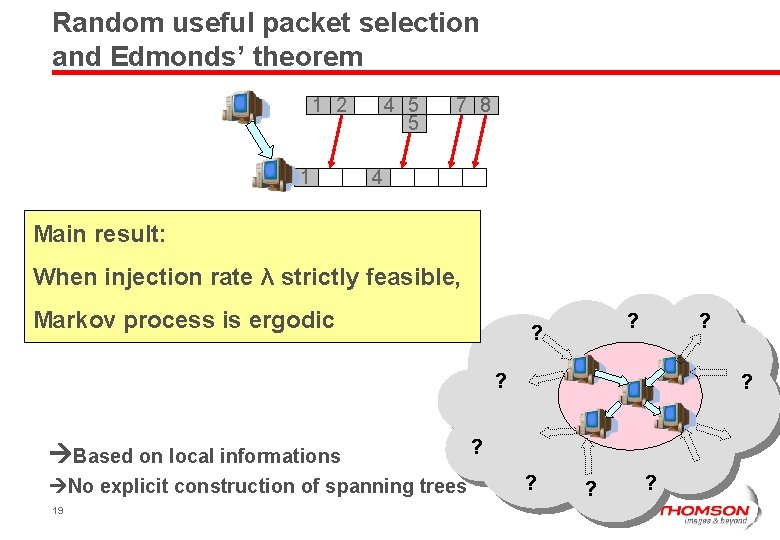
Random useful packet selection and Edmonds’ theorem 1 2 1 4 5 5 7 8 4 Main result: When injection rate λ strictly feasible, Markov process is ergodic ? ? Based on local informations No explicit construction of spanning trees 19 ? ? ?

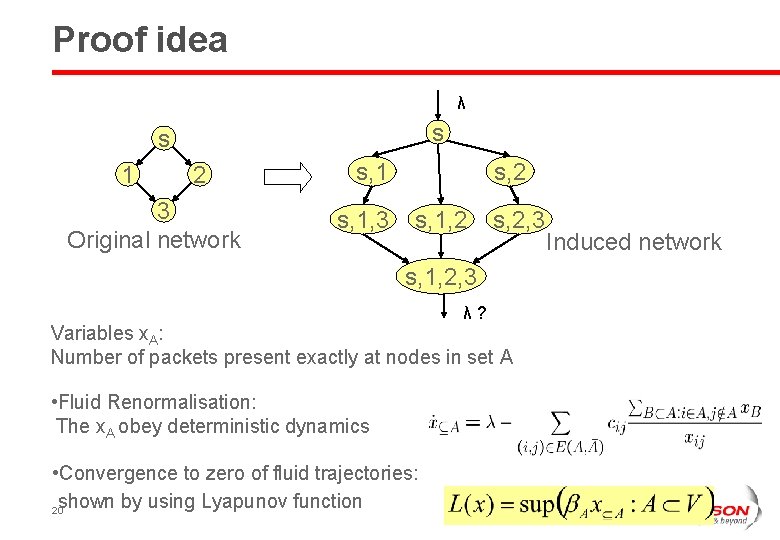
Proof idea λ s s 1 2 3 Original network s, 1, 3 s, 2 s, 1, 2 s, 2, 3 s, 1, 2, 3 λ? Variables x. A: Number of packets present exactly at nodes in set A • Fluid Renormalisation: The x. A obey deterministic dynamics • Convergence to zero of fluid trajectories: shown by using Lyapunov function 20 Induced network

Comments Provides “analytical” proof of Edmond’s theorem l Delays? l 21

Conclusions l Epidemic diffusion – Straightforward implementation – Efficient use of bandwidth resources l 22 Random & local decisions lead to global optimum

Outlook l Open problems – Schemes both delay- and rate- optimal? – Concurrent stream diffusions? – Stability proofs without the Lyapunov function? 23