Environmental and Exploration Geophysics II Amplitude Frequency and

Environmental and Exploration Geophysics II Amplitude, Frequency and Bandwidth and their relationship to Seismic Resolution tom. h. wilson@geo. wvu. edu Department of Geology and Geography West Virginia University Morgantown, WV

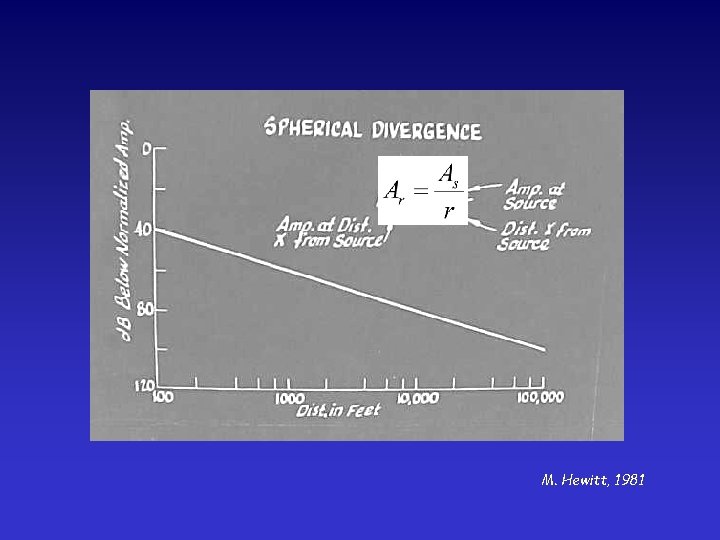
M. Hewitt, 1981

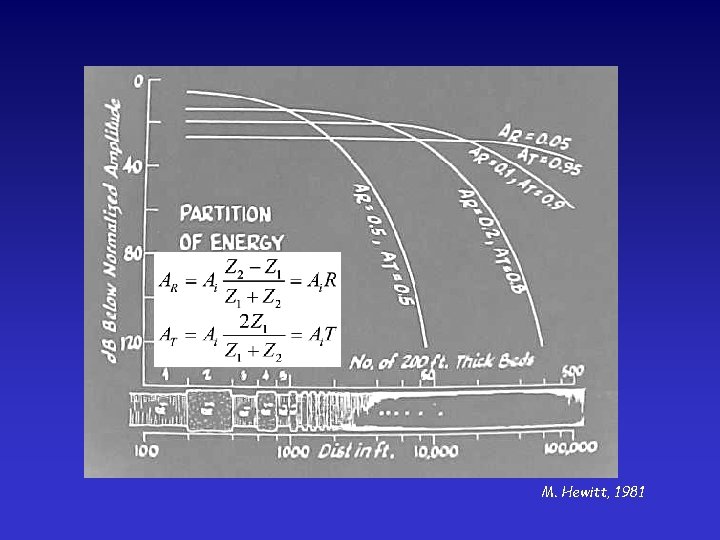
M. Hewitt, 1981

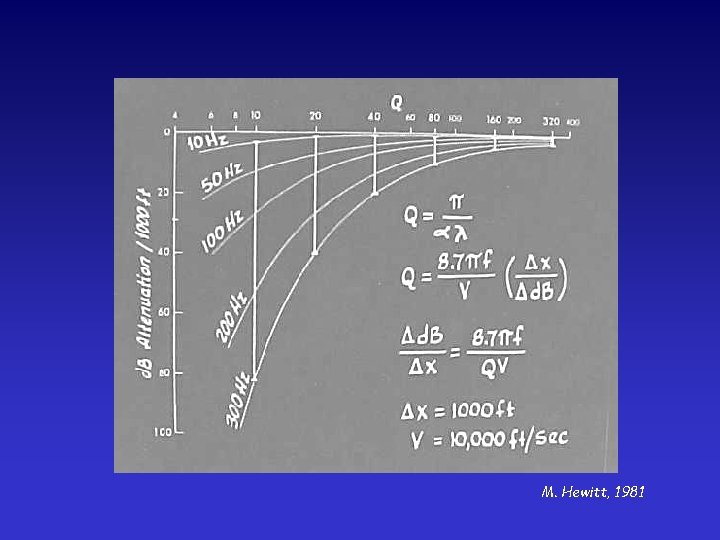
M. Hewitt, 1981

M. Hewitt, 1981

M. Hewitt, 1981

<more absorptive … less absorptive> M. Hewitt, 1981

When surface irregularities have wavelengths similar to the wavelengths comprising the wavelet, significant scattering will occur. The surface appears rough to the wavelet. When surface irregularities are small compared to the wavelengths comprising the wavelet, scattering losses are small. The surface “appears smoother to the incident wavelet.

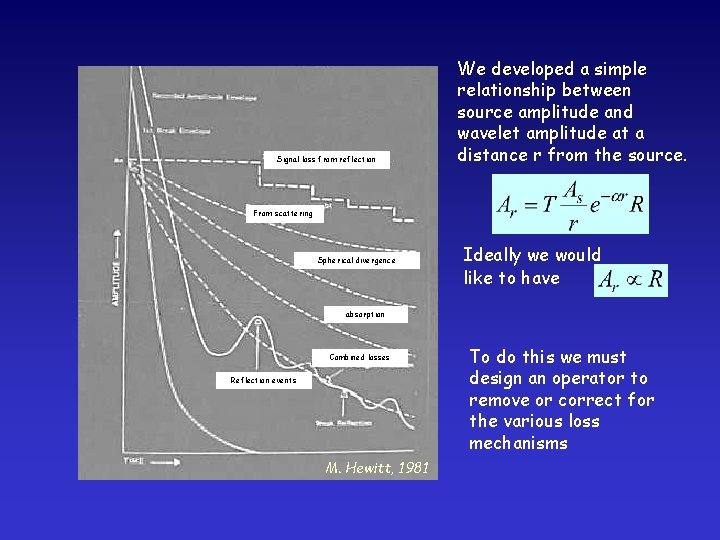
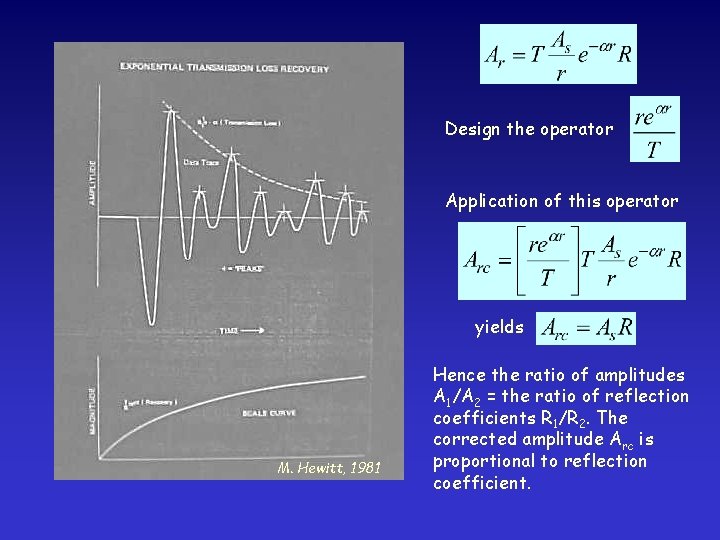
Signal loss from reflection We developed a simple relationship between source amplitude and wavelet amplitude at a distance r from the source. From scattering Spherical divergence Ideally we would like to have absorption Combined losses Reflection events M. Hewitt, 1981 To do this we must design an operator to remove or correct for the various loss mechanisms

Design the operator Application of this operator yields M. Hewitt, 1981 Hence the ratio of amplitudes A 1/A 2 = the ratio of reflection coefficients R 1/R 2. The corrected amplitude Arc is proportional to reflection coefficient.

The relative amplitude differences shown in the high fidelity section (lefttop) provide more accurate information about actual differences in reflection coefficient and thus lithology than does the section below.

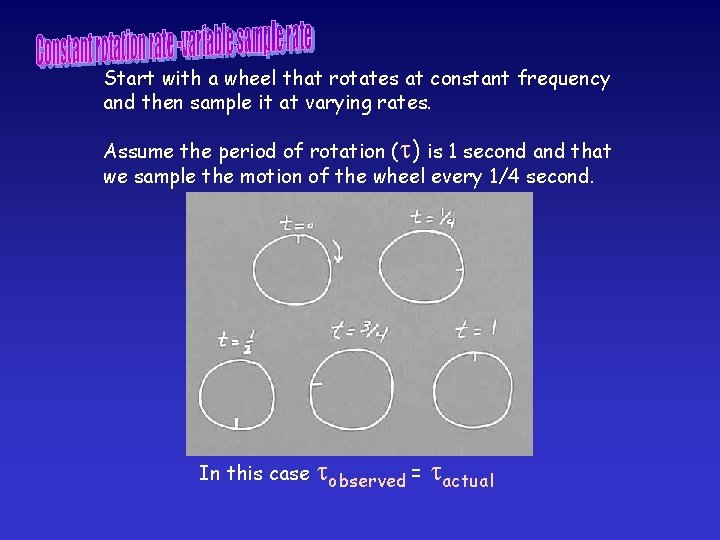
From the start you have been aware that seismic data is recorded as a series of measurements made at constant time intervals - the sample interval. How do we decide what the sample rate should be? How often should ground motion be sampled to accurately represent it? The example of a rotating wheel with spokes serves as the best example of the possible effect of sample rate on the conclusions of our observations concerning the motion of the wheel.

Start with a wheel that rotates at constant frequency and then sample it at varying rates. Assume the period of rotation ( ) is 1 second and that we sample the motion of the wheel every 1/4 second. In this case observed = actual

Let t = 1/2 second We estimate = 1 but we are unable to determine the direction of wheel rotation.

Let t = 3/4 second Our estimate of = 3 seconds is in error - by 300%

When t = 1 second, the wheel appears to remain at the starting point but actually makes a single rotation between samples.

In the second case, we deal with situations where the sample interval t is constant and varies. Take the case = 1/2 second and =4 seconds. the period of rotation where t We have no problem in this case accurately delineating the period of rotation. Note that f = 1/4 second, and that f t =1/8 th. f t is the fraction of a cycle the wheel has moved in time t.

When t equals 1/2 we also correctly identify rotation periods of 1. 5 seconds. f t = 1/3 rd

As before, when = 1, and t = 1/2, we are still able to identify the period as 1 second. f t = 1/2

However, when = 3/4 sec, the frequency f =1/ = 1. 33 cycles per second. Between consecutive samples, the wheel will turn through f t cycles (check units). f t =2/3 rds cycle between samples. The output period is 1. 5 seconds and the output frequency is 2/3 rds cycle per second. Our estimate of in this case is twice its actual value.

When = 2/3 seconds, the frequency of rotation, f=1. 5 cycles/sec. Thus the wheel turns through f t or 3/4 cycles between samples. The wheel appears to move counterclockwise with frequency equal to 1/2 cycle per second ( = 2 seconds). When = 1/2 second, the frequency of rotation, f=2 cycles/sec. f t =1. Thus the wheel turns through one cycle between samples. The wheel appears fixed. The output frequency is 0.

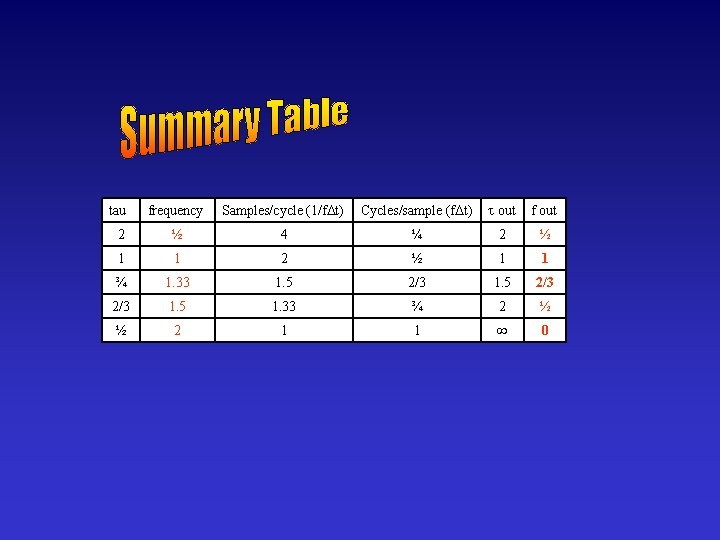
tau frequency Samples/cycle (1/f t) Cycles/sample (f t) out f out 2 ½ 4 ¼ 2 ½ 1 1 ¾ 1. 33 1. 5 2/3 2/3 1. 5 1. 33 ¾ 2 ½ ½ 2 1 1 0

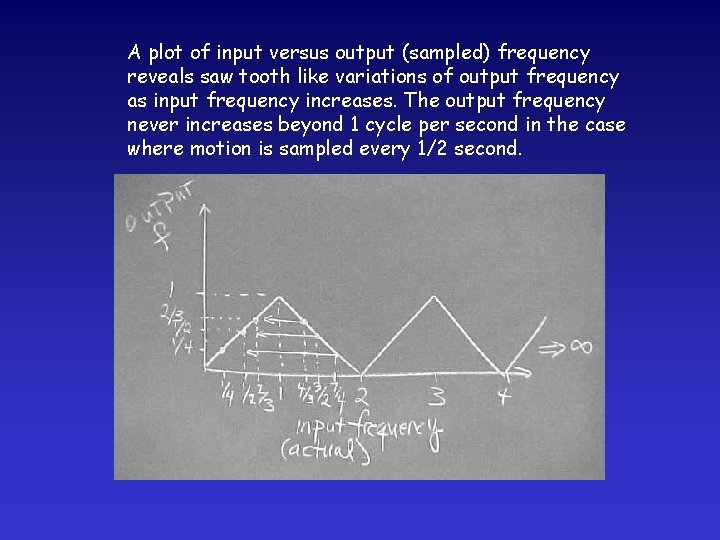
A plot of input versus output (sampled) frequency reveals saw tooth like variations of output frequency as input frequency increases. The output frequency never increases beyond 1 cycle per second in the case where motion is sampled every 1/2 second.

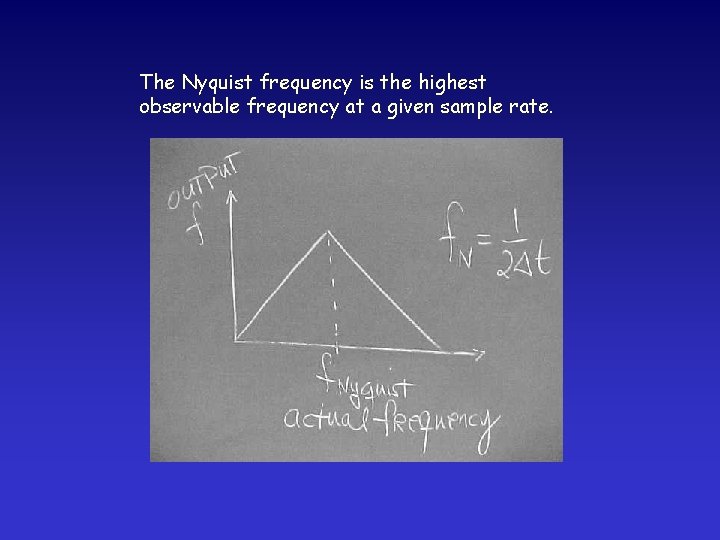
The Nyquist frequency is the highest observable frequency at a given sample rate.

Higher input frequencies appear to have lower frequency in the output recording. This phenomena is referred to as frequency or signal aliasing.

Hilterman, 1985

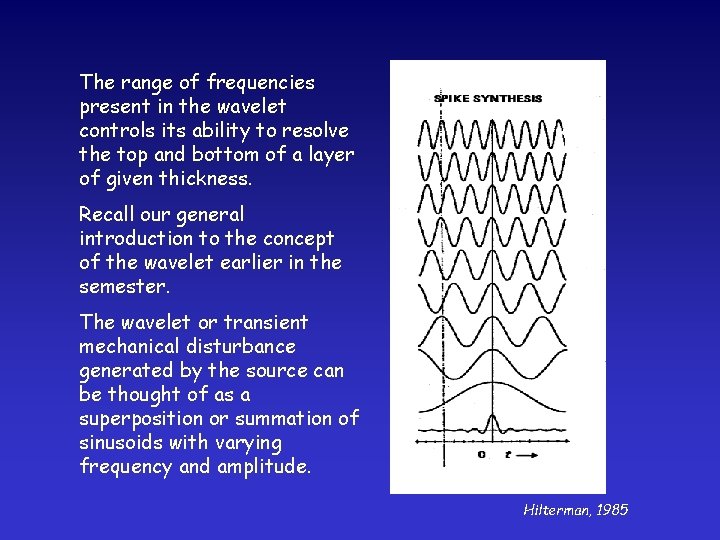
The range of frequencies present in the wavelet controls its ability to resolve the top and bottom of a layer of given thickness. Recall our general introduction to the concept of the wavelet earlier in the semester. The wavelet or transient mechanical disturbance generated by the source can be thought of as a superposition or summation of sinusoids with varying frequency and amplitude. Hilterman, 1985

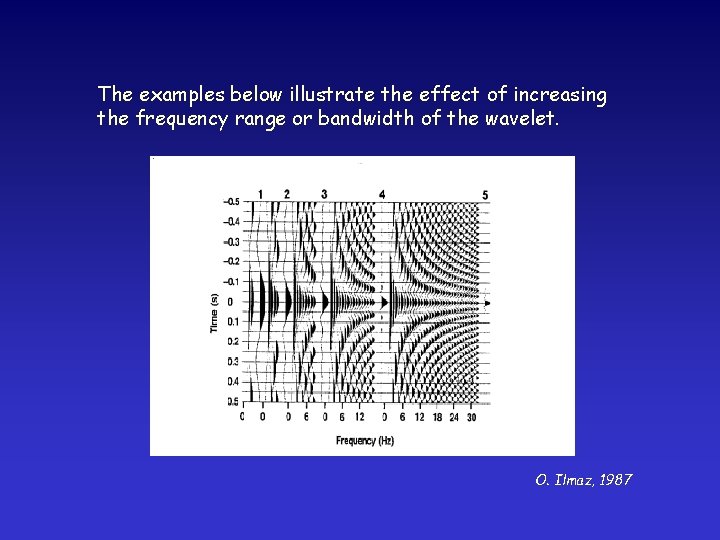
The examples below illustrate the effect of increasing the frequency range or bandwidth of the wavelet. O. Ilmaz, 1987

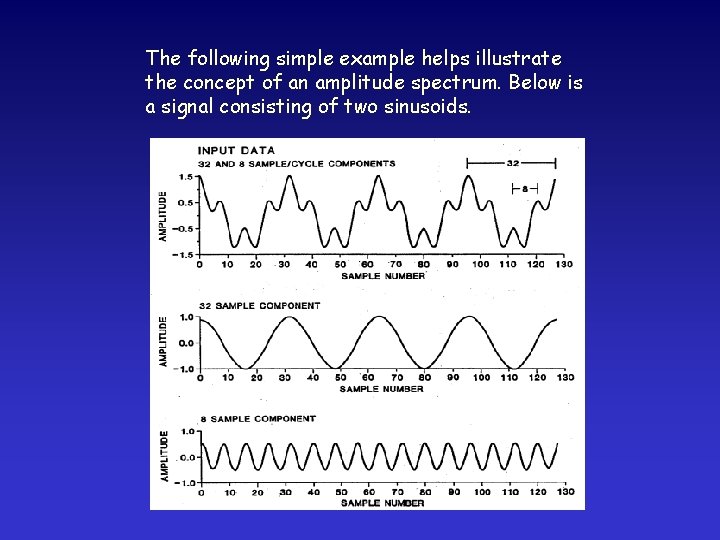
The following simple example helps illustrate the concept of an amplitude spectrum. Below is a signal consisting of two sinusoids.

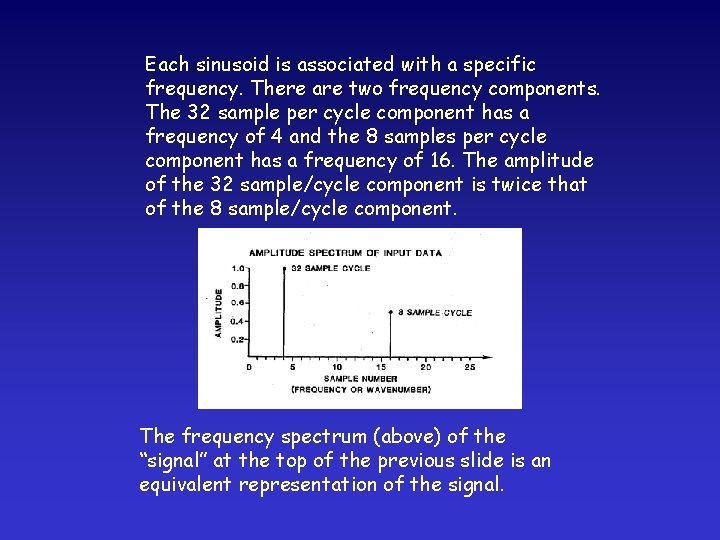
Each sinusoid is associated with a specific frequency. There are two frequency components. The 32 sample per cycle component has a frequency of 4 and the 8 samples per cycle component has a frequency of 16. The amplitude of the 32 sample/cycle component is twice that of the 8 sample/cycle component. The frequency spectrum (above) of the “signal” at the top of the previous slide is an equivalent representation of the signal.

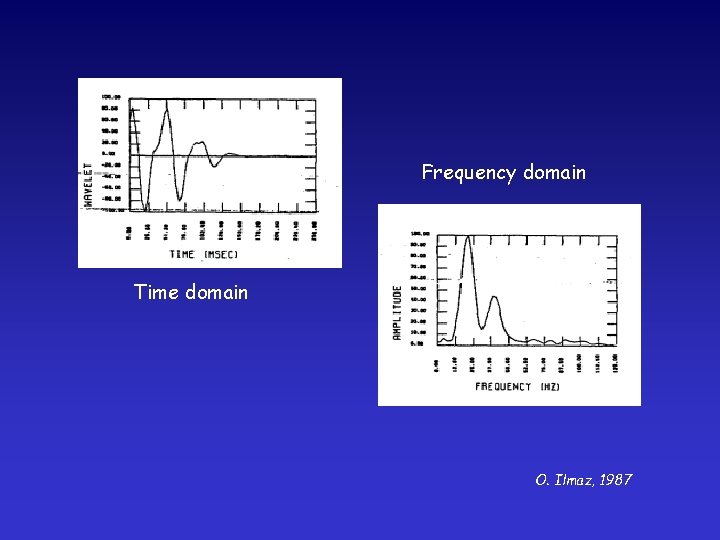
Frequency domain Time domain O. Ilmaz, 1987

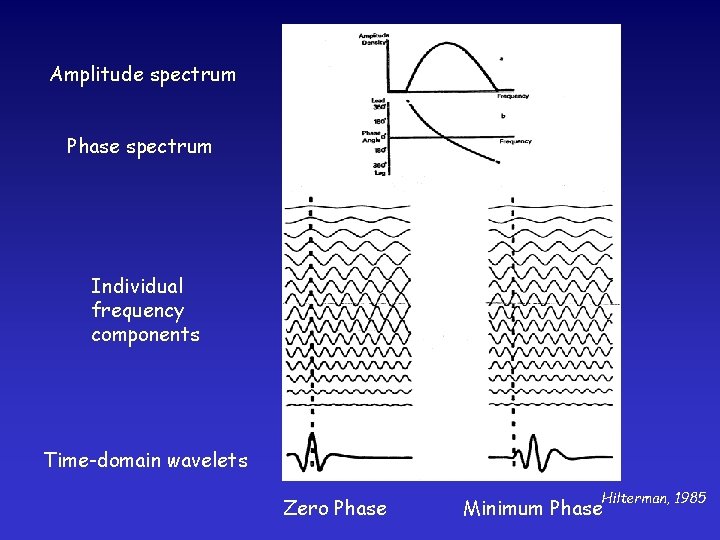
Amplitude spectrum Phase spectrum Individual frequency components Time-domain wavelets Zero Phase Hilterman, 1985 Minimum Phase