Enumration des permutations motif exclu Stage effectu au

Enumération des permutations à motif exclu Stage effectué au DSI de l’université de Florence, Italie, sous la direction de Renzo Pinzani. 16/09/2004 1

Plan de l’exposé • • • Les grands principes de la méthode ECO L’exemple des chemins de Dyck Définition et résultats à connaître sur les permutations à motif(s) exclu(s) Le problème spécifique des permutations à motif exclu de longueur fixée Une nouvelle statistique sur les permutations évitant un motif généralisé de type (1, 2) ou (2, 1) 16/09/2004 2

Méthode ECO : l’idée essentielle ECO = Enumeration of Combinatorial Objects • • • Une classe d’objets combinatoires munie d’un paramètre Étudier comment le nombre d’objets évolue en fonction de la valeur du paramètre Envisager une construction récursive des objets combinatoires considérés 16/09/2004 3

Méthode ECO : aspects théoriques • • • Classe C munie d’un paramètre p (=taille) Cn = {x Є C | p(x) = n } Trouver un opérateur θ : C -> 2 C tel que θ(Cn) = Cn+1 et qui ne génère pas de doublons θ fonctionne en insérant un petit bloc d’objet dans des sites actifs. Ensemble des sites actifs = frontière. 16/09/2004 4

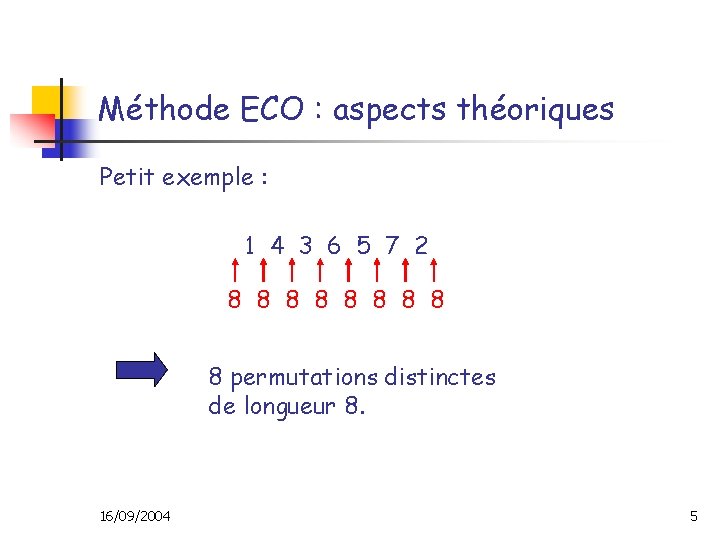
Méthode ECO : aspects théoriques Petit exemple : 1 4 3 6 5 7 2 8 8 8 8 8 permutations distinctes de longueur 8. 16/09/2004 5

Méthode ECO : aspects théoriques Θ vérifie deux conditions : • Pour tout Y Є Cn+1, il existe X Є Cn tel que Y Є θ(X) • Pour tous X 1 et X 2 Є Cn , si X 1 ≠ X 2, alors 16/09/2004 U θ(X 1) θ(X 2) = Ø 6

Méthode ECO : aspects théoriques • • • Θ ~ description récursive de la classe C. Mène parfois à une équation fonctionnelle vérifiée par la fonction génératrice de C. Fonction génératrice : T(x) = Σn Є N an xn où an est le cardinal de Cn. 16/09/2004 7

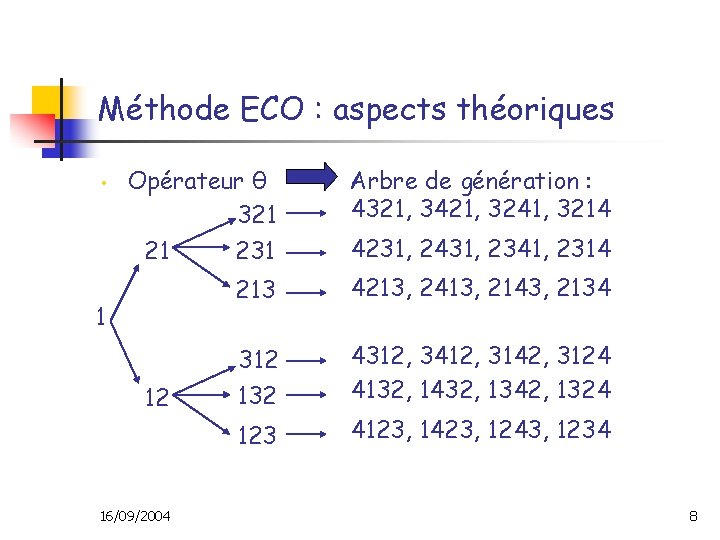
Méthode ECO : aspects théoriques • Opérateur θ 321 21 231 Arbre de génération : 4321, 3421, 3241, 3214 213 4213, 2413, 2143, 2134 312 132 4312, 3412, 3142, 3124 4132, 1432, 1342, 1324 123 4123, 1423, 1243, 1234 1 12 16/09/2004 4231, 2431, 2341, 2314 8

Méthode ECO : aspects théoriques Règles de réécriture : • • Chaque objet a une étiquette. Une étiquette permet seule de trouver les étiquettes des fils. Souvent étiquette de X = nombre de fils de X = cardinal de θ(X) 16/09/2004 9

Méthode ECO : aspects théoriques Exemple d’une règle de réécriture : (2) (k) 16/09/2004 > (2) (3). . . (k) (k+1) 10

Exemple : les chemins de Dyck 16/09/2004 11

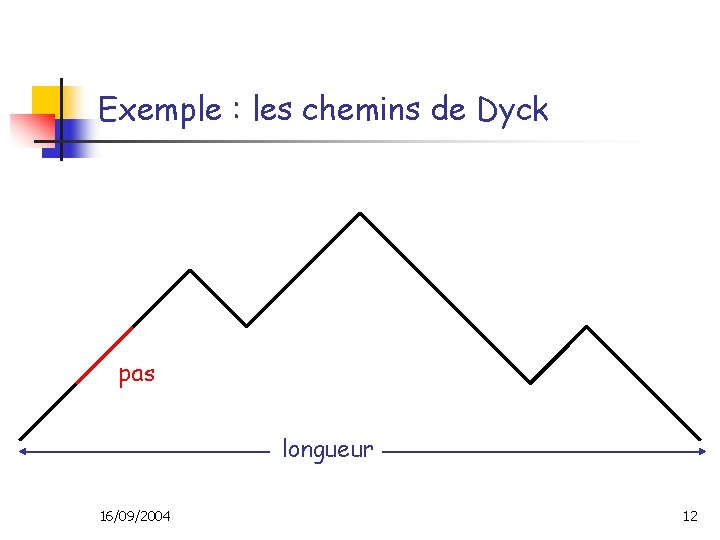
Exemple : les chemins de Dyck pas longueur 16/09/2004 12

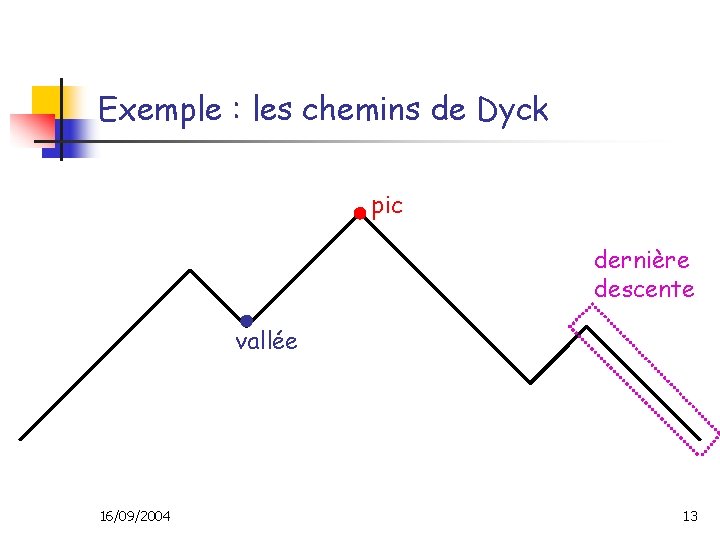
Exemple : les chemins de Dyck pic dernière descente vallée 16/09/2004 13

Exemple : les chemins de Dyck • # pas NE = # pas SE = demi-longueur • Dn = {chemins de Dyck de longueur 2 n} • • d Є Dn , θ(d) = {chemins obtenus à partir de d en insérant un pic dans chaque point de la dernière descente de d} Frontière = {points de la dernière descente de d} 16/09/2004 14

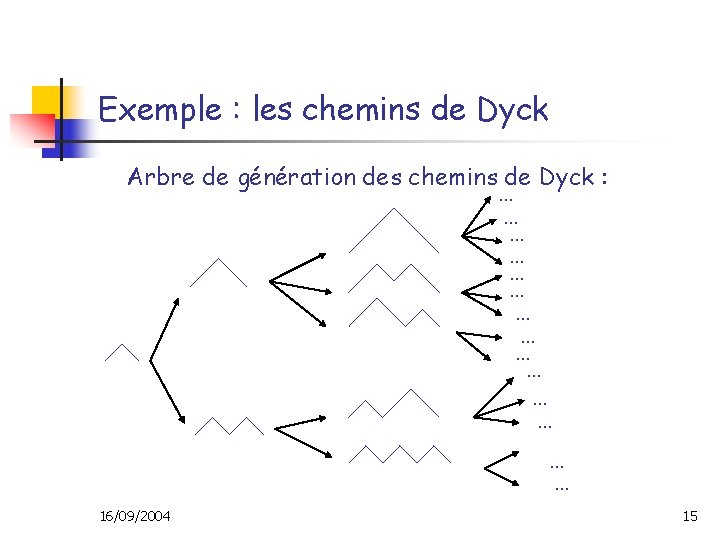
Exemple : les chemins de Dyck Arbre de génération des chemins de Dyck : … … … … 16/09/2004 15

Exemple : les chemins de Dyck • • • Étiquette = nombre de sites actifs = nombre de points de la dernière descente Étiquette du chemin de Dyck racine : (2) d Є D avec k sites actifs -> k chemins de Dyck avec des dernières descentes contenant 2, 3, …, k, k+1 points 16/09/2004 16

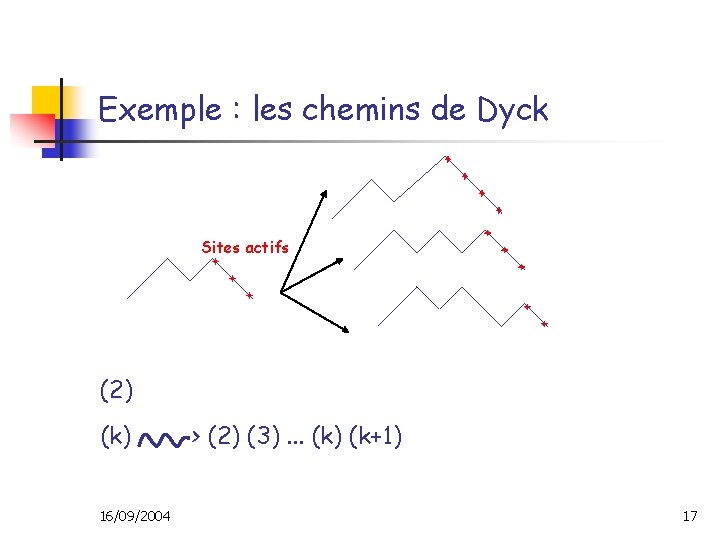
Exemple : les chemins de Dyck Sites actifs (2) (k) 16/09/2004 > (2) (3). . . (k) (k+1) 17

Exemple : les chemins de Dyck dЄD • n(d) = demi-longueur et f(d) = # frontière • Fonction génératrice : T(x, y) = Σd Є D xn(d)yf(d) • • • On cherche T(x, 1). T(x, y) = xy²+ Σd Є D ΣiЄ{2, …, f(d)+1}xn(d)+1 yi Après calcul : T(x, y) = xy²[1 + (y-1)-1(T(x, y) – T(x, 1)) ] 16/09/2004 18

Exemple : les chemins de Dyck • T(x, 1) = (1 -4 x)1/2 )(2 x)-1 -1 Fonction génératrice des nombres de Catalan ! T(x, 1) = Σd Є D xn(d) = Σn Є N an xn avec an = #Dn Conclusion : #Dn = Cn = (n+1)-1 16/09/2004 ( 2 nn ) 19

Permutations à motif(s) exclu(s) • • • Sn = ensemble des permutations de {1, 2, …, n} S est l’union des Sn , n Є N. Une représentation des permutations : π : 1 -> 4 4 -> 2 2 -> 6 5 -> 3 3 -> 1 6 -> 5 π=461235 16/09/2004 20

Permutations à motif(s) exclu(s) • • Soient π et σ deux permutations, telles que π est plus longue que σ. σ est appelée un motif. Notons n la longueur de π et m celle de σ. π contient σ s’il existe 1 ≤ i 1 < i 2 < i 3 < i 4 <… < im ≤ n tels que π(i 1)π(i 2)π(i 3)π(i 4)…π(im) soit isomorphe en ordre à σ. π évite σ dans le cas contraire. 16/09/2004 21

Permutations à motif(s) exclu(s) • • • Exemple de permutation contenant un motif : 15682437 contient le motif 312. Exemple de permutation évitant un motif : 85143267 évite le motif 231. On s’intéresse à l’énumération des permutations à motif(s) exclu(s). On note Sn(P) les permutations de longueur n évitant l’ensemble de motifs P. 16/09/2004 22

Permutations à motif(s) exclu(s) • • • Les motifs généralisés : 1 -23, 12 -3, 1 -32, 13 -2, 2 -13, 21 -3, 2 -31, 23 -1, 3 -12, 31 -2, 3 -21, 32 -1. Ils sont de type (1, 2) ou (2, 1) selon le nombre d’éléments avant et après le tiret. Notion de permutation contenant ou évitant un motif généralisé : comme pour les motifs classiques, mais les deux chiffres adjacents dans le motif doivent correspondre à deux éléments adjacents dans la permutation. 16/09/2004 23

Permutations à motif(s) exclu(s) • • • Exemple de permutation contenant le motif généralisé 21 -3 : 1452376. Une permutation peut contenir 123 sans contenir 12 -3 : 7162534 par exemple. Il en va de même pour tous les motifs généralisés. 16/09/2004 24

Permutations à motif(s) exclu(s) • Opérations de miroir et de complément : • πr (i) = π(n+1 -i) c • π (i) = n+1 -π(i) • Les trois classes de symétrie : {1 -23, 3 -21, 32 -1, 12 -3} Catalan Cn {3 -12, 21 -3, 1 -32, 23 -1} Catalan Cn {2 -13, 31 -2, 2 -31, 13 -2} Bell Bn 16/09/2004 25

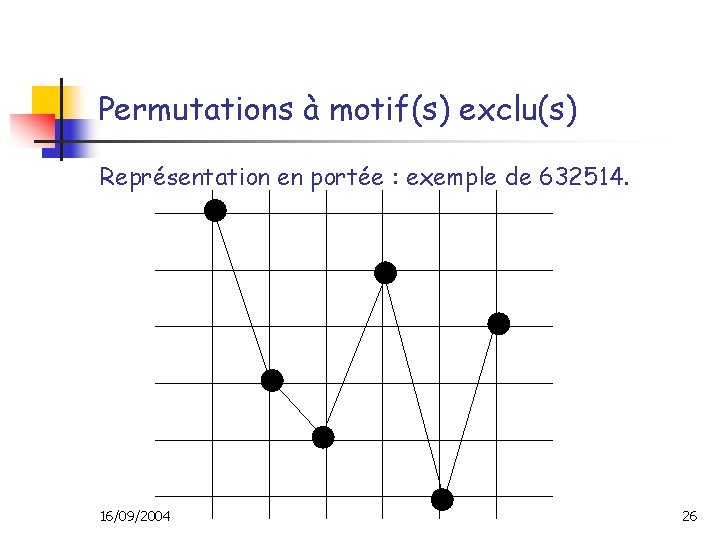
Permutations à motif(s) exclu(s) Représentation en portée : exemple de 632514. 16/09/2004 26

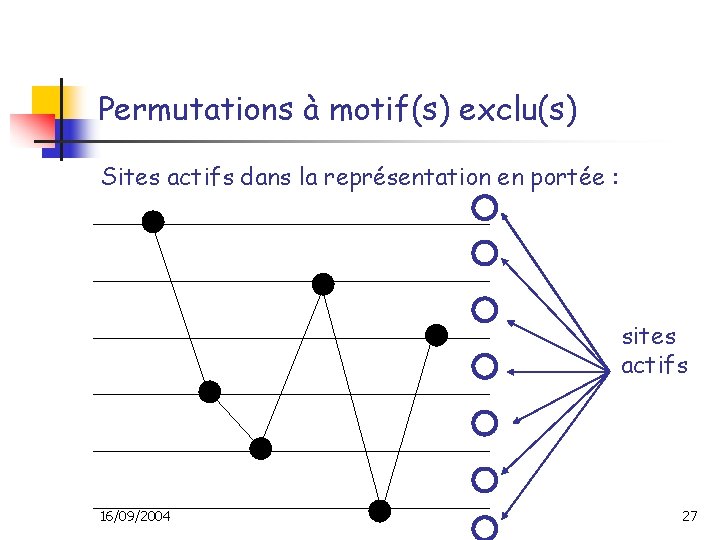
Permutations à motif(s) exclu(s) Sites actifs dans la représentation en portée : sites actifs 16/09/2004 27

Permutations à motif(s) exclu(s) Génération des permutations filles : 16/09/2004 28

Sujet particulier du stage Enumération des permutations à motif exclu de longueur fixée … 16/09/2004 29

Les motifs 1 -k 2 et 2 -k 1 • • • π Є Sn évite 1 -k 2(resp. 2 -k 1) si pour tout i, π(i) > π(i+k+1) (resp. π(i) < π(i+k+1) ) 1 -k 2 et 2 -k 1 sont miroirs l’un de l’autre, donc l’énumération des permutations évitant 1 -k 2 suffit. Pour 1 -02, il existe unique permutation dans chaque Sn qui évite ce motif : celle qui est décroissante. 16/09/2004 30

Les motifs 1 -k 2 et 2 -k 1 • Étude pour 1 -12 avec la méthode ECO et la représentation en portée. • Étiquette de π Є Sn(1 -12) : (π(n-1), π(n)). • Si π Є Sn(1 -12), alors π(n-1)=1 ou π(n)=1. • Étiquettes de la forme (1, x) ou (x, 1). 16/09/2004 31

Les motifs 1 -k 2 et 2 -k 1 Construction de la règle de réécriture : • • La permutation 1 ne rentre pas dans le cas général de l’étiquetage. Les permutations 12 et 21 évitent le motif 1 -k 2 et ont pour étiquettes respectives (1, 2) et (2, 1). 16/09/2004 32

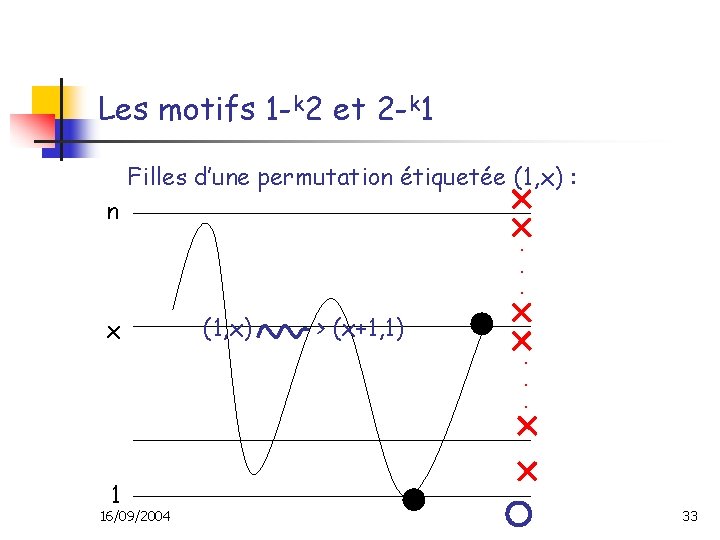
Les motifs 1 -k 2 et 2 -k 1 Filles d’une permutation étiquetée (1, x) : n. . . x 1 16/09/2004 (1, x) > (x+1, 1). . . 33

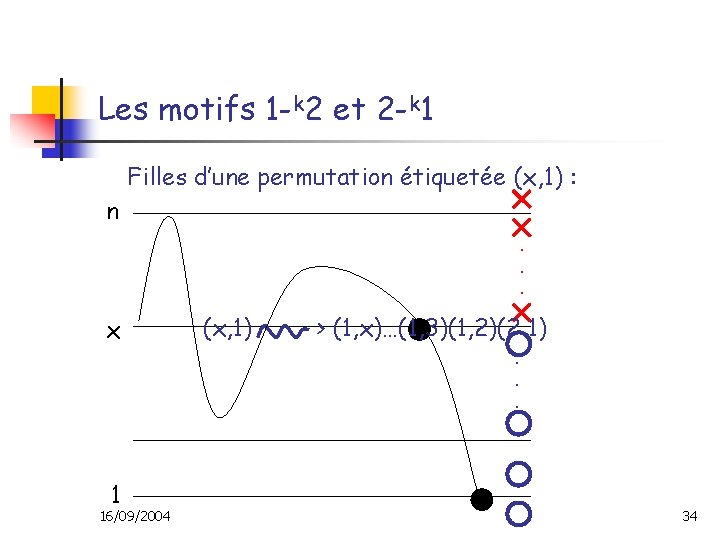
Les motifs 1 -k 2 et 2 -k 1 Filles d’une permutation étiquetée (x, 1) : n. . . x 1 16/09/2004 (x, 1) > (1, x)…(1, 3)(1, 2)(2, 1). . . 34

Les motifs 1 -k 2 et 2 -k 1 • • Remarque (2, 1) produit (1, 2) et (2, 1) donc la permutation 1 est logiquement étiquetée (2, 1). Règle de réécriture : (2, 1) (x, 1) > (1, x)…(1, 3)(1, 2)(2, 1) (1, x) > (x+1, 1) • Résultat : # Sn(1 -1 2) = n! / ([n/2]! [(n+1)/2]!) 16/09/2004 35

Les motifs 1 -k 2 et 2 -k 1 • • Étude pour 1 -22 : règle de réécriture à étiquettes triples… Calcul des premières valeurs permet de formuler une conjecture : #Sn(1 -22) = n! / ([n/3]! [(n+1)/3]! [(n+2)/3]!) Similaire à #Sn(1 -12) = n! / ([n/2]! [(n+1)/2]!) Idée : #Sn(1 -k 2) = n! / ([n/(k+1)]! [(n+1)/(k+1)]! … [(n+k)/(k+1)]!) 16/09/2004 36

Les motifs 1 -k 2 et 2 -k 1 Exemple des permutations évitant 1 -32 : #&@$#&@$#&@$#&@$#&@ Comme pour 1 -02, la séquence des #, celle des &, celle des @ et celle des $ sont des décroissantes. Il suffit de constituer 4 paquets de la bonne taille, de classer leur éléments par ordre décroissant et d’écrire les paquets en quinconce. 16/09/2004 37

Perm. à motif exclu de longueur fixée • • • Définitions : Les motifs de longueur fixée sont les suivants : {1 -k 23, 12 -k 3, 1 -k 32, 13 -k 2, 2 -k 13, 21 -k 3, 2 -k 31, 23 -k 1, 3 -k 12, 31 -k 2 3 -k 21 32 -k 1 : k Є N*} Comme précédemment, le symbole –k exprime un saut de k éléments. Par exemple, π évite 1 -k 32 s’il n’existe aucun indice i tel que π(i) < π(i+k+2) < π(i+k+1). 16/09/2004 38

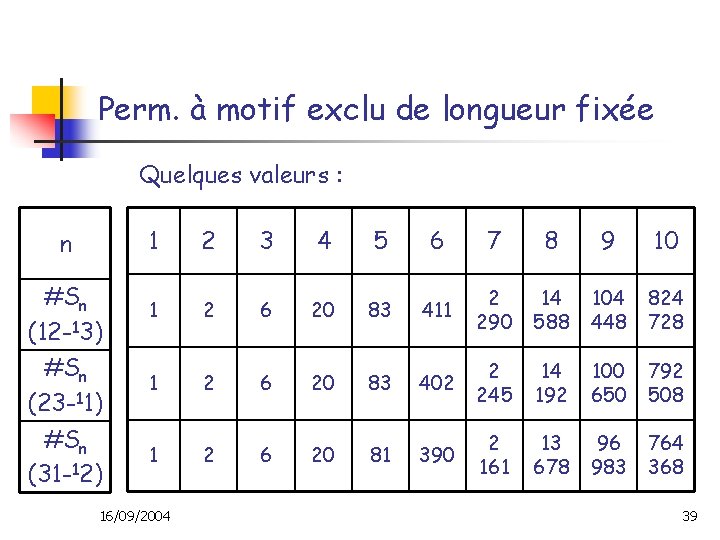
Perm. à motif exclu de longueur fixée Quelques valeurs : n 1 2 3 4 5 6 7 8 9 10 #Sn (12 -13) 1 2 6 20 83 411 2 290 14 588 104 448 824 728 #Sn (23 -11) 1 2 6 20 83 402 2 245 14 192 100 650 792 508 #Sn (31 -12) 1 2 6 20 81 390 2 161 13 678 96 983 764 368 16/09/2004 39

Perm. à motif exclu de longueur fixée • • • Nombreuses voies de recherche explorées. Aucune fructueuse… Règles de réécriture complexes… mais on peut tenter une étude. On cherche à dégager une méthode à partir des règles de réécriture des motifs généralisés sans la contrainte de longueur. Cette étude réserve de belles surprises ! 16/09/2004 40

Le résultat principal du stage • • Il s’agit d’une nouvelle statistique sur les permutations évitant un motif généralisé de type (1, 2) ou (2, 1) : la distribution de ces permutations selon la longueur et la valeur du premier (ou du dernier) élément. Résultat pour un motif dans chaque classe de symétrie, puis opérateur miroir et complément pour étendre le résultat aux autres motifs. 16/09/2004 41

Distribution des perm. évitant 1 -23 • • • Étude grâce à la méthode ECO, avec une représentation en portée des permutations. Règle de réécriture. Arbre de génération. Obtention d’une matrice dont les coefficients satisfont une récurrence, et calcul d’une forme close de ces coefficients. Interprétation des coefficients de cette matrice. Distribution selon la longueur et la valeur du dernier élément des permutations évitant 1 -23. 16/09/2004 42

Distribution des perm. évitant 1 -23 • Étiquette d’une permutation de Sn(1 -23) possédant k sites actifs : (k, n). • Soit π Є Sn(1 -23) étiquetée par (k, n). • Distinguons deux cas selon que π(n) = 1 ou non. 16/09/2004 43

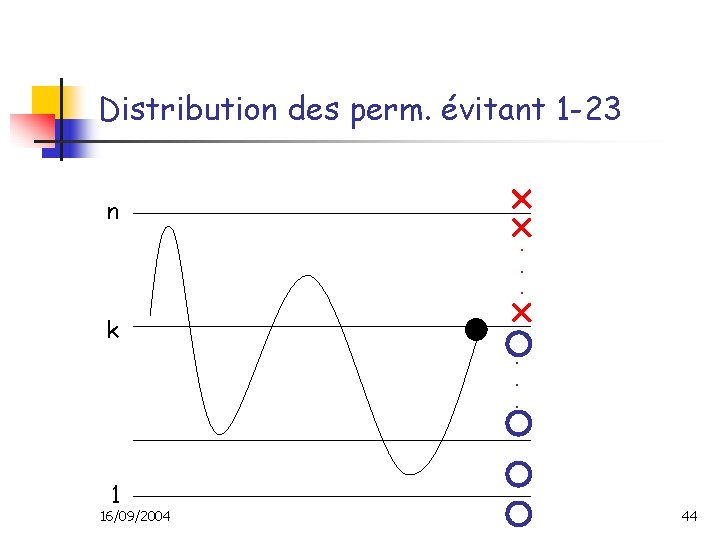
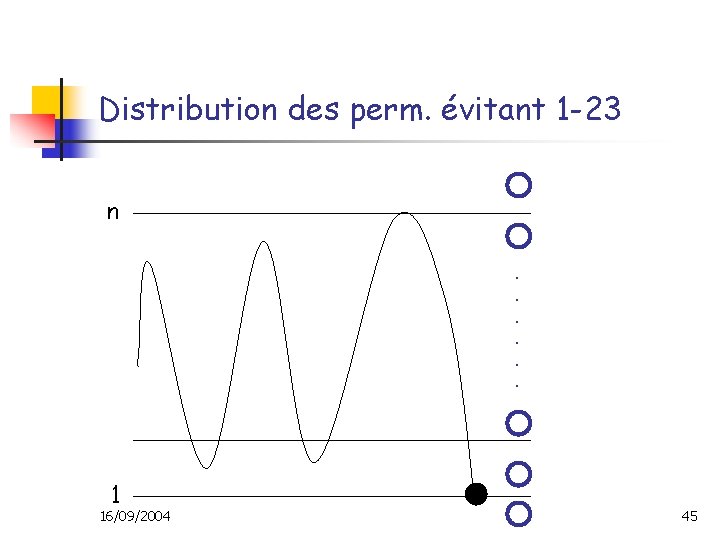
Distribution des perm. évitant 1 -23 n. . . k 1 16/09/2004 . . . 44

Distribution des perm. évitant 1 -23 n. . . 1 16/09/2004 45

Distribution des perm. évitant 1 -23 En résumé : • π Є Sn(1 -23) telle que π(n)=k≠ 1 génère k permu-tations de Sn+1(1 -23) finissant par 1, 2, …, k. • π Є Sn(1 -23) telle que π(n)=1 génère n+1 permu-tations de Sn+1(1 -23) finissant par 1, 2, …, n+1. • • π Є Sn(1 -23) telle que π(n)=k≠ 1 a pour étiquette (k, n). π Є Sn(1 -23) telle que π(n)=1 a pour étiquette (n+1, n). 16/09/2004 46

Distribution des perm. évitant 1 -23 Règle de réécriture : (2, 1) (k, n) (k) 16/09/2004 > (2, n+1)(3, n+1)…(k, n+1) (n+2, n+1) > (2) (3) … (k) (n+2) 47

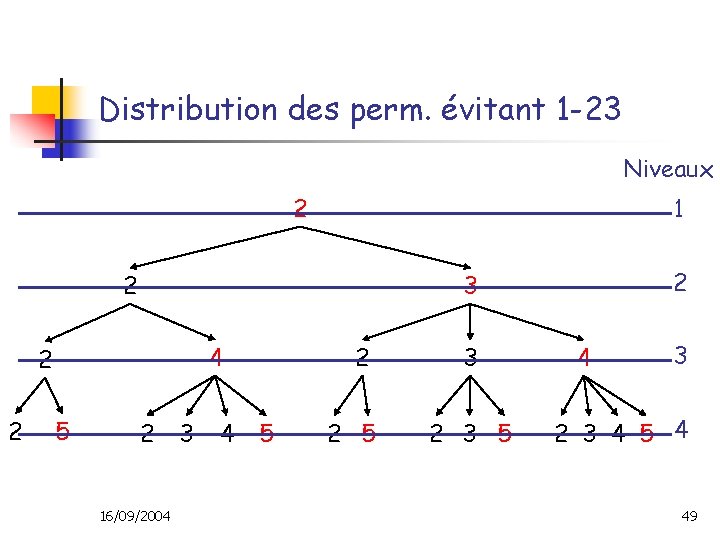
Distribution des perm. évitant 1 -23 Arbre de génération simplifié à partir de la règle de réécriture simplifiée : Au niveau n dans l’arbre de génération, une étiquette (k) a pour filles (2) (3) … (k) et (n+2) au niveau n+1. 16/09/2004 48

Distribution des perm. évitant 1 -23 Niveaux 2 1 2 4 2 2 5 2 3 2 16/09/2004 3 4 2 5 3 2 3 5 4 3 2 3 4 5 4 49

Distribution des perm. évitant 1 -23 • On construit une matrice M telle que M(i, j) représente le nombre d’étiquettes j+1 au niveau i. 1 0 0 0. . . 1 1 0 0. . . 2 1 2 0 0 0. . . 5 3 2 5 0 0. . . 15 10 7 5 15 0. . . 52 37 27 20 15 52. . . 16/09/2004 50

Distribution des perm. évitant 1 -23 • • • Récurrence dans M : M(n, k) = Σk ≤i≤ n-1 M(n-1, i). Deux points importants pour l’interprétation des coefficients de M : • π Є Sn(1 -23) a k sites actifs ssi π(n)=k, 2≤k≤n. • π Є Sn(1 -23) a n+1 sites actifs ssi π(n)=1. Transfert de la diagonale en première colonne pour obtenir la matrice de distribution cherchée. 16/09/2004 51

Distribution des perm. évitant 1 -23… … selon la longueur (indices des lignes) et la valeur du dernier élément (indices des colonnes) : matrice A = 1 2 3 4 5 6 1 1 0 0 0. . . 2 1 1 0 0. . . 3 2 2 1 0 0 0. . . 4 5 5 3 2 0 0. . . 5 15 15 10 7 5 0. . . 6 52 52 37 27 20 15. . . 16/09/2004 52

Distribution des perm. évitant 1 -23… • • Calcul des coefficients de A : la récurrence sur M se transforme en une récurrence sur A qui se simplifie en A(n, k) = A(n, k-1) – A(n, k-2). Forme close des coefficients de A : A(n, k) = ∆k-2(Bn-1). 16/09/2004 53

Conclusion • Distribution des permutations évitant 1 -23 selon leur longueur et la valeur dernier élément : • #{π Є Sn(1 -23) : π(n) = 1} = Bn-1 , n ≥ 1 • #{π Є Sn(1 -23) : π(n) = k} = ∆k-2(Bn-1) , 2 ≤ k ≤ n 16/09/2004 54

Conclusion • • • Ce résultat s’étend aux autres éléments de la classe de symétrie de 1 -23 par miroir et complément. Pour les autres classes de symétrie, les études menées pour 3 -12 et 2 -13 mènent à des résultats similaires. Pour chaque motif généralisé : une nouvelle statistique. 16/09/2004 55

Conclusion • • Après l’étude pour un motif exclu, on se demande souvent ce qui se passe quand on étudie les permutations évitant simultanément plusieurs motifs. Première étude pour la paire de motifs 1 -23 et 1 -32 a donné une statistique plus faible… mais tout reste à explorer ! 16/09/2004 56