Enumeration of Time Series Motifs of All Lengths

Example: Repeating Pattern (Motif) 30 20 10 0 0 2000 0 Chiu et al.

Motivation: Enumerating Motifs Find the most similar pairs of time series at every lengths.

Outline 1. Bounding correlation 2. Enumerating motifs of all lengths ◦ Intuitive Example ◦

Correlation Advantage: 1. Scale and Shift invariant 2. Linear scans to compute Disadvantage: 1.

Bounding Euclidean Distance 10 9 8 7 6 5 4 3 1 2 3

Intuition Append 20 and re-normalize Append 10 and re-normalize Normalized 2 2 2 1.

Bounding Euclidean Distance 35 Normalized Distance 30 25 25 24 23. 5 23 22.

Intuition -7 x 103 -7. 5 -8 -8. 5 0 1000 2000 3000 4000

Sanity Check 4 2 0 -2 White Noise 0 1000 2000 3000 4000 5

Experimental Results: Scalability 6 5 4 x 104 18 Smart Brute Force EEG EOG

D D Activity Recognition H. Pohl et al. SMC 2010 Step Action A Side

Experimental Results 8 10 n=10 k n=20 k n=40 k n=80 k n=160 k

Sample Output -7 x 103 -7. 5 -8 -8. 5 0 1000 2000 1.

Time Series Join x 1. 5 x 10 -3 Correlation Length-adjusted Correlation 2 2

Motif Covering Locations of the First Occurrences 8000 6000 Covering Motifs 4000 2000 0

Slides: 26

Download presentation

Enumeration of Time Series Motifs of All Lengths ABDULLA H MUEEN DEPART MENT OF C OMP UT ER SC IENCE UNIVE RSIT Y OF NEW MEXIC O

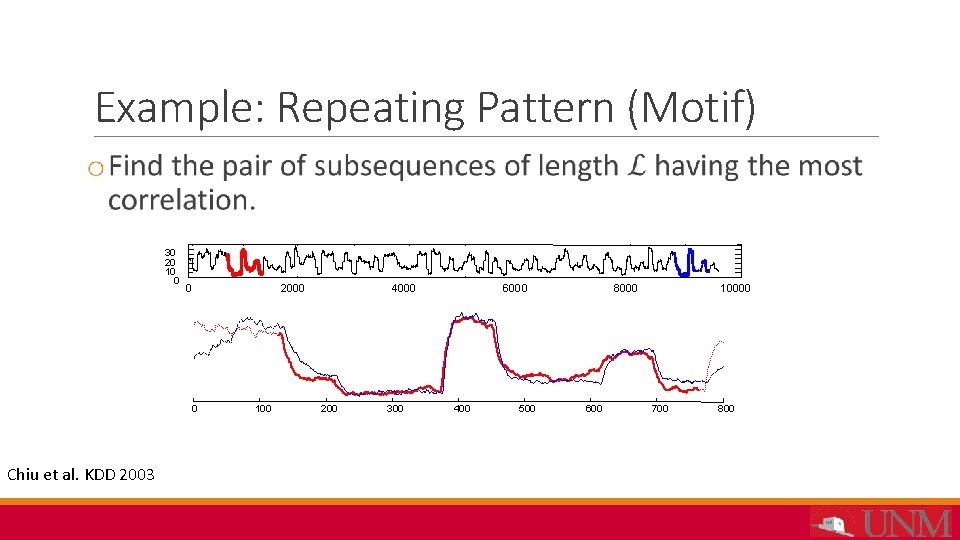
Example: Repeating Pattern (Motif) 30 20 10 0 0 2000 0 Chiu et al. KDD 2003 100 4000 200 300 6000 400 500 8000 600 10000 700 800

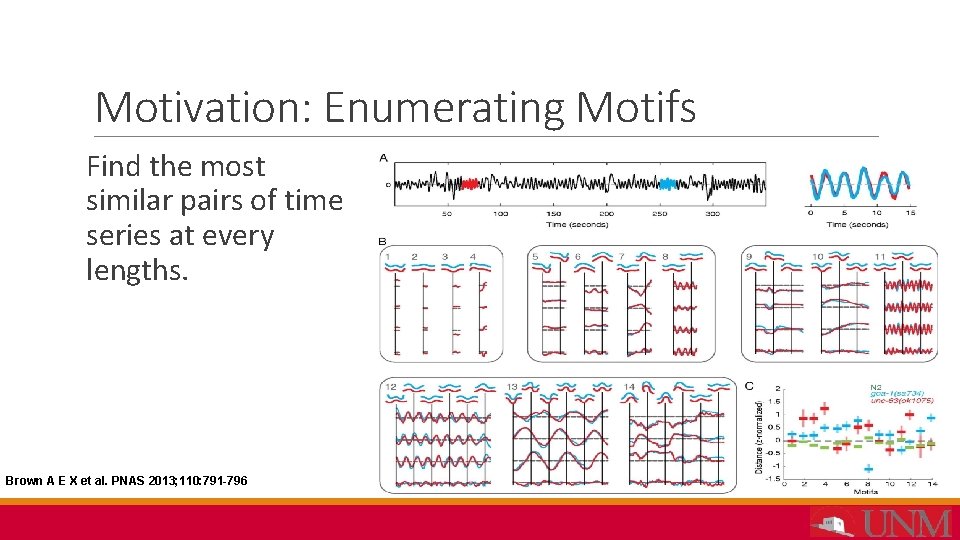
Motivation: Enumerating Motifs Find the most similar pairs of time series at every lengths. Brown A E X et al. PNAS 2013; 110: 791 -796

Goals: Enumerating Motifs

Outline 1. Bounding correlation 2. Enumerating motifs of all lengths ◦ Intuitive Example ◦ Experimental Results ◦ Case Study: Activity Recognition 3. Conclusion

Pearson’s Correlation Coefficient

Correlation Advantage: 1. Scale and Shift invariant 2. Linear scans to compute Disadvantage: 1. Don’t consider warping 2. Is not a metric

Relationship with Euclidean Distance

Bounding Euclidean Distance 10 9 8 7 6 5 4 3 1 2 3 4 Without Normalization 5 4 3 2 1 0 -1 -2 -3 -4 Values Changed 1 2 3 With Normalization 4 5

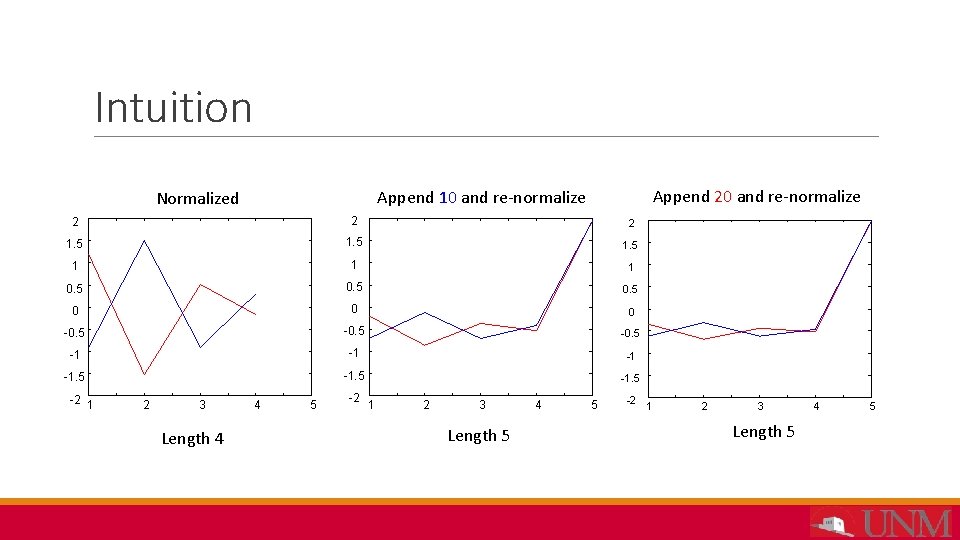
Intuition Append 20 and re-normalize Append 10 and re-normalize Normalized 2 2 2 1. 5 1 1 1 0. 5 0 0 0 -0. 5 -1 -1. 5 -2 1 2 3 Length 4 4 5 -2 1 2 3 Length 5 4 5

Bounding Euclidean Distance

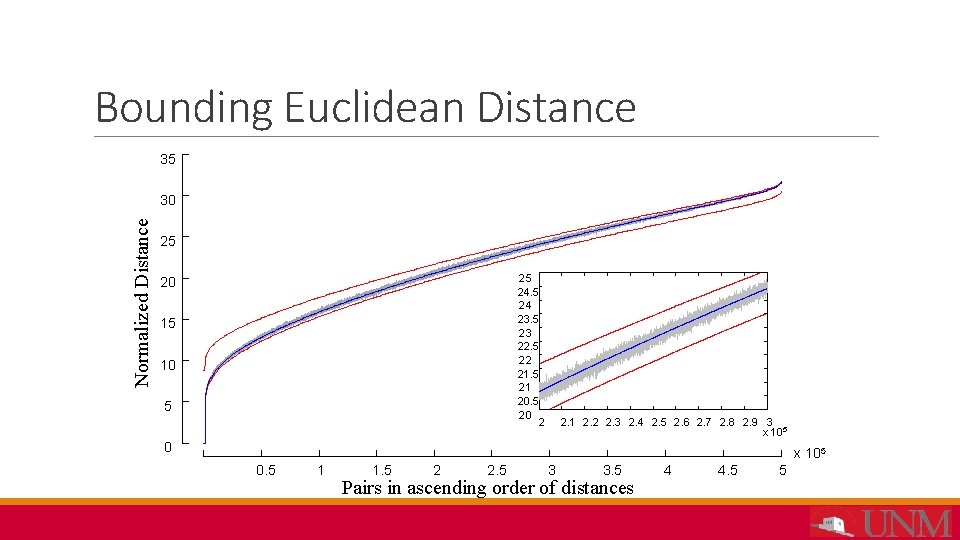
Bounding Euclidean Distance 35 Normalized Distance 30 25 25 24 23. 5 23 22. 5 22 21. 5 21 20. 5 20 2 20 15 10 5 2. 1 2. 2 2. 3 2. 4 2. 5 2. 6 2. 7 2. 8 2. 9 3 x 105 0. 5 1 1. 5 2 2. 5 3 3. 5 Pairs in ascending order of distances 4 4. 5 5

Outline 1. Bounding correlation 2. Enumerating motifs of all lengths ◦ Intuitive Example ◦ Experimental Results ◦ Case Study: Activity Recognition 3. Conclusion

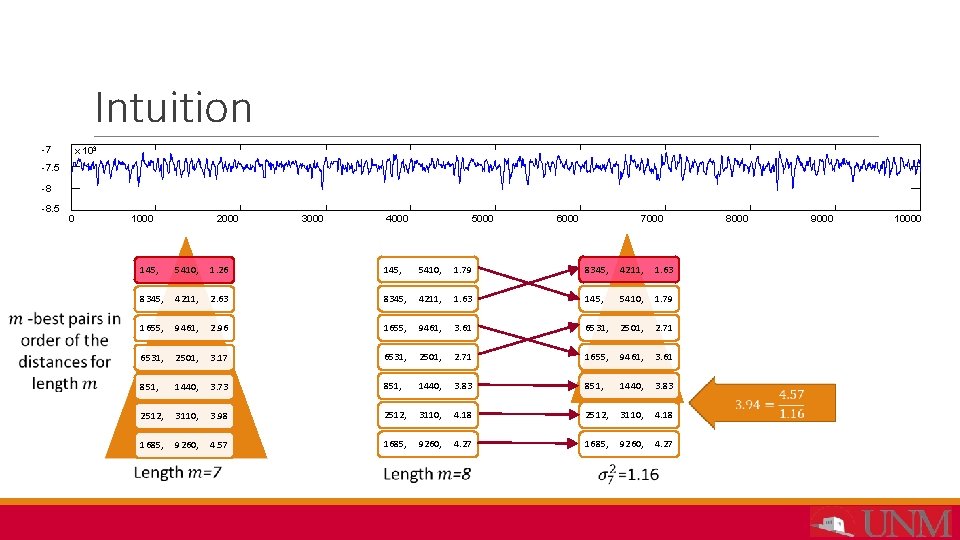
Intuition -7 x 103 -7. 5 -8 -8. 5 0 1000 2000 3000 4000 5000 6000 7000 145, 5410, 1. 26 145, 5410, 1. 79 8345, 4211, 1. 63 8345, 4211, 2. 63 8345, 4211, 1. 63 145, 5410, 1. 79 1655, 9461, 2. 96 1655, 9461, 3. 61 6531, 2501, 2. 71 6531, 2501, 3. 17 6531, 2501, 2. 71 1655, 9461, 3. 61 851, 1440, 3. 73 851, 1440, 3. 83 2512, 3110, 3. 98 2512, 3110, 4. 18 1685, 9260, 4. 57 1685, 9260, 4. 27 8000 9000 10000

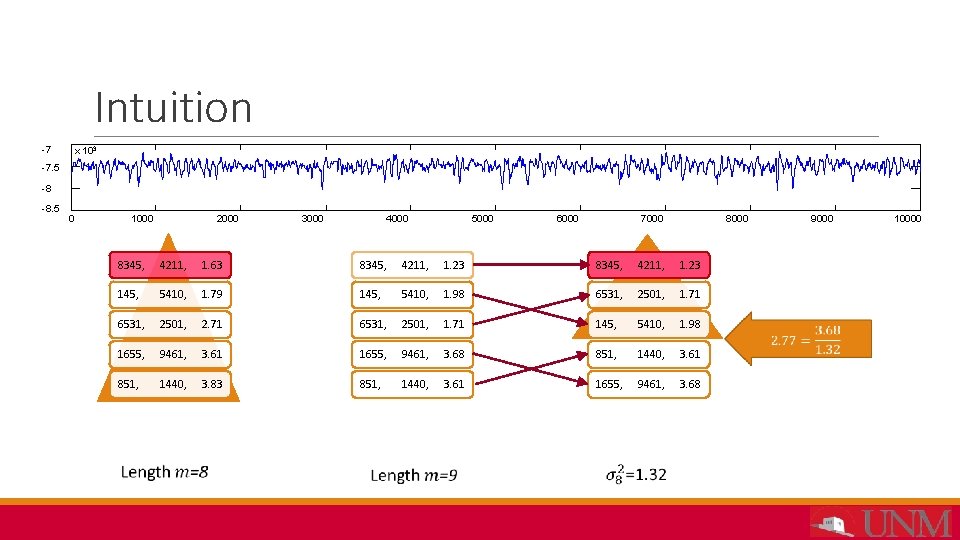
Intuition -7 x 103 -7. 5 -8 -8. 5 0 1000 2000 3000 4000 5000 6000 7000 8345, 4211, 1. 63 8345, 4211, 1. 23 145, 5410, 1. 79 145, 5410, 1. 98 6531, 2501, 1. 71 6531, 2501, 2. 71 6531, 2501, 1. 71 145, 5410, 1. 98 1655, 9461, 3. 61 1655, 9461, 3. 68 851, 1440, 3. 61 851, 1440, 3. 83 851, 1440, 3. 61 1655, 9461, 3. 68 9000 10000

Outline 1. Bounding correlation 2. Enumerating motifs of all lengths ◦ Intuitive Example ◦ Experimental Results ◦ Case Study: Activity Recognition 3. Conclusion

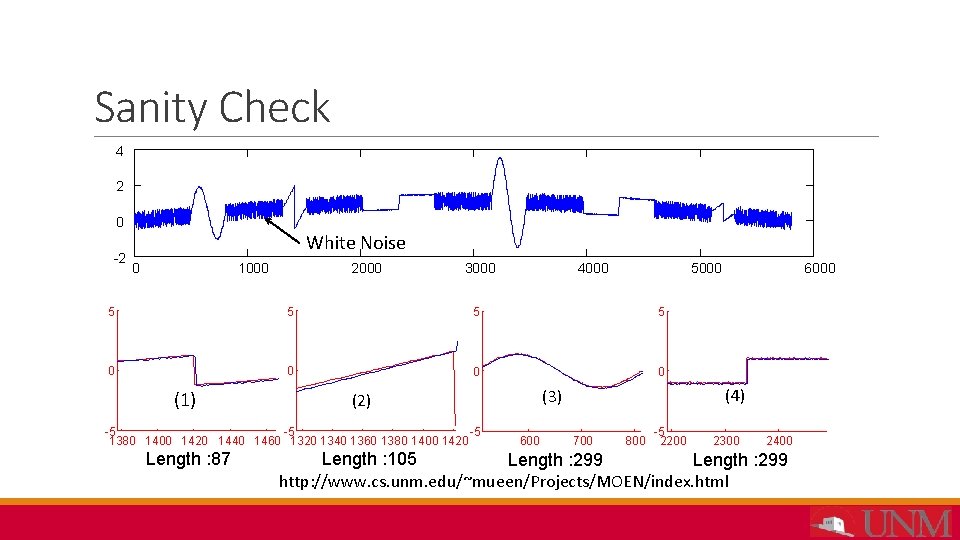
Sanity Check 4 2 0 -2 White Noise 0 1000 2000 3000 4000 5 5 5 5 0 0 (1) -5 -5 -5 1380 1400 1420 1440 1460 1320 1340 1360 1380 1400 1420 Length : 87 (4) (3) (2) 6000 700 800 -5 2200 2300 2400 Length : 105 Length : 299 http: //www. cs. unm. edu/~mueen/Projects/MOEN/index. html

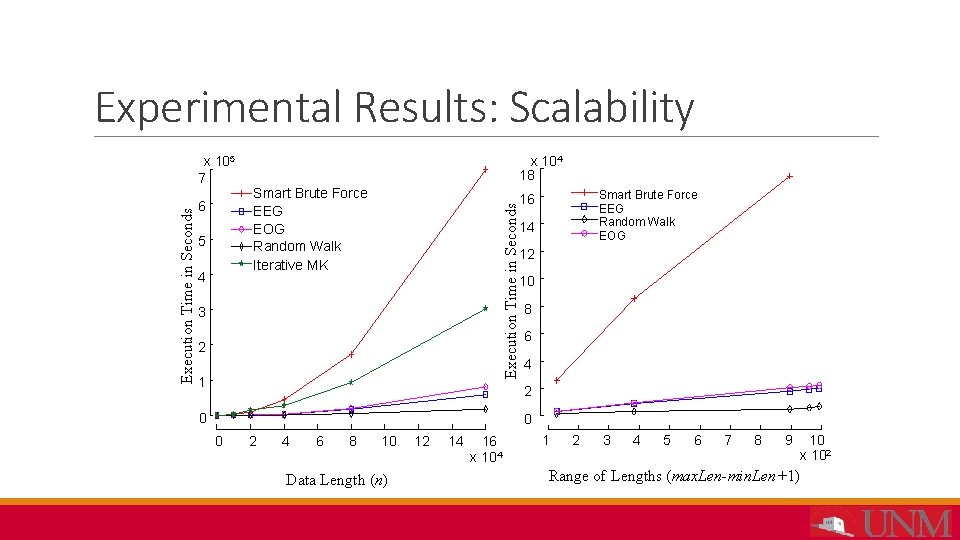
Experimental Results: Scalability 6 5 4 x 104 18 Smart Brute Force EEG EOG Random Walk Iterative MK Smart Brute Force EEG Random Walk EOG 16 Execution Time in Seconds x 105 7 14 12 10 3 2 1 8 6 4 2 0 0 0 2 4 6 8 10 Data Length (n) 12 14 16 x 104 1 2 3 4 5 6 7 8 9 Range of Lengths (max. Len-min. Len+1) 10 x 102

Outline 1. Bounding correlation 2. Enumerating motifs of all lengths ◦ Intuitive Example ◦ Experimental Results ◦ Case Study: Activity Recognition 3. Conclusion

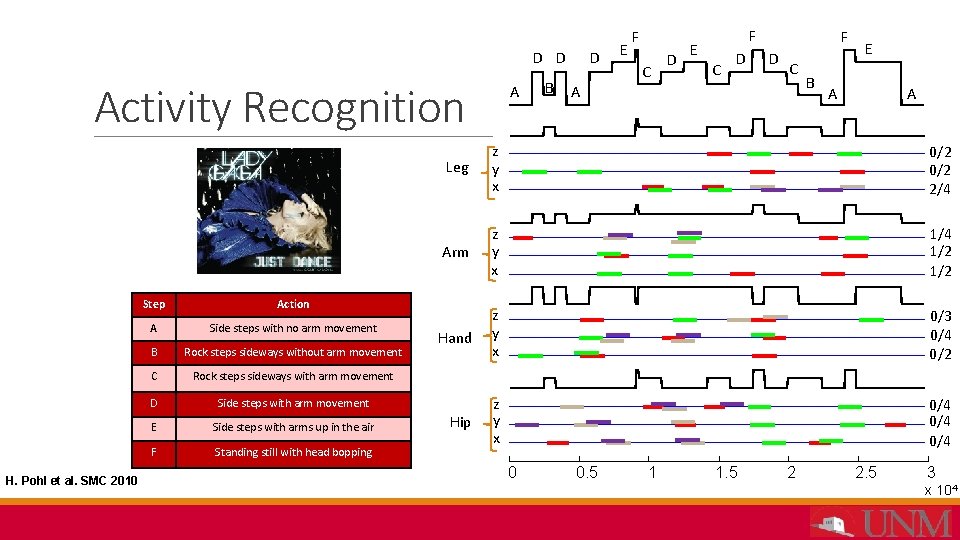
D D Activity Recognition H. Pohl et al. SMC 2010 Step Action A Side steps with no arm movement B Rock steps sideways without arm movement C Rock steps sideways with arm movement D Side steps with arm movement E Side steps with arms up in the air F Standing still with head bopping A B D E F C D F E C D F D C A B E A A Leg z y x 0/2 2/4 Arm z y x 1/4 1/2 Hand z y x 0/3 0/4 0/2 Hip z y x 0/4 0/4 0 0. 5 1 1. 5 2 2. 5 3 x 104

Thank You

Backup Slides

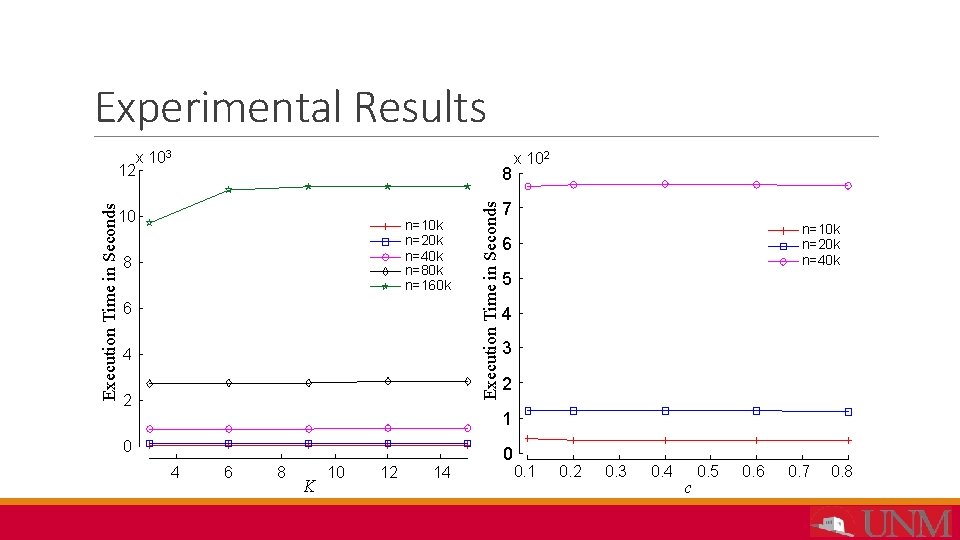
Experimental Results 8 10 n=10 k n=20 k n=40 k n=80 k n=160 k 8 6 4 2 Execution Time in Seconds 12 x 103 x 102 7 n=10 k n=20 k n=40 k 6 5 4 3 2 1 0 4 6 8 K 10 12 14 0 0. 1 0. 2 0. 3 0. 4 c 0. 5 0. 6 0. 7 0. 8

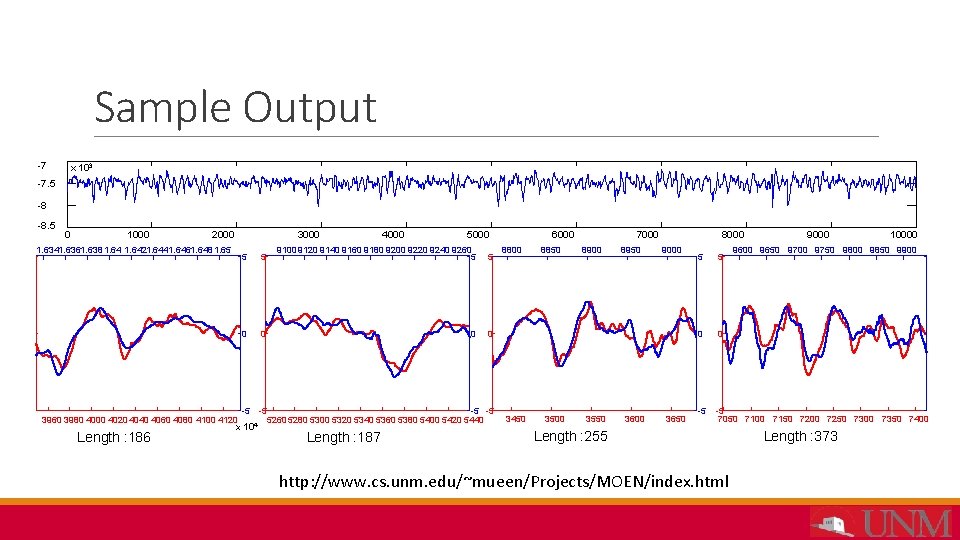
Sample Output -7 x 103 -7. 5 -8 -8. 5 0 1000 2000 1. 6341. 6361. 638 1. 6421. 6441. 6461. 648 1. 65 3000 4000 5 5 9100 9120 9140 9160 9180 9200 9220 9240 9260 5 5 0 0 -5 -5 3960 3980 4000 4020 4040 4060 4080 4100 4120 5260 5280 5300 5320 5340 5360 5380 5400 5420 5440 4 x 10 Length : 186 Length : 187 6000 8800 3450 8850 3500 7000 8900 3550 8950 3600 8000 9000 3650 9000 10000 9650 9700 9750 9800 9850 9900 5 5 0 0 -5 -5 7050 7100 7150 7200 7250 7300 7350 7400 Length : 255 http: //www. cs. unm. edu/~mueen/Projects/MOEN/index. html Length : 373

Time Series Join x 1. 5 x 10 -3 Correlation Length-adjusted Correlation 2 2 1. 5 1 1 0. 5 Best Match 0 100 200 300 400 500 Lengths 0 600 700 800

Motif Covering Locations of the First Occurrences 8000 6000 Covering Motifs 4000 2000 0 0 50 100 150 200 Length 250 300 350 400