Entry Task TRAPEZOIDS AND KITES Lesson 6 6

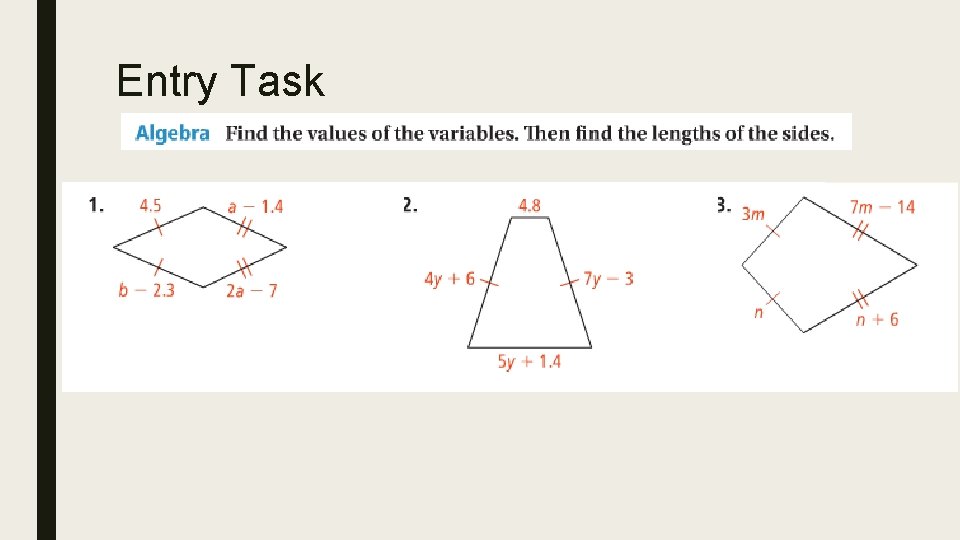
Entry Task

TRAPEZOIDS AND KITES Lesson 6 -6

Learning Targets ■ I will be able to: – Explore kites and trapezoids and make conjectures about their properties; – Prove theorems about kites and trapezoids; – Use properties of kites and trapezoids to solve problems.

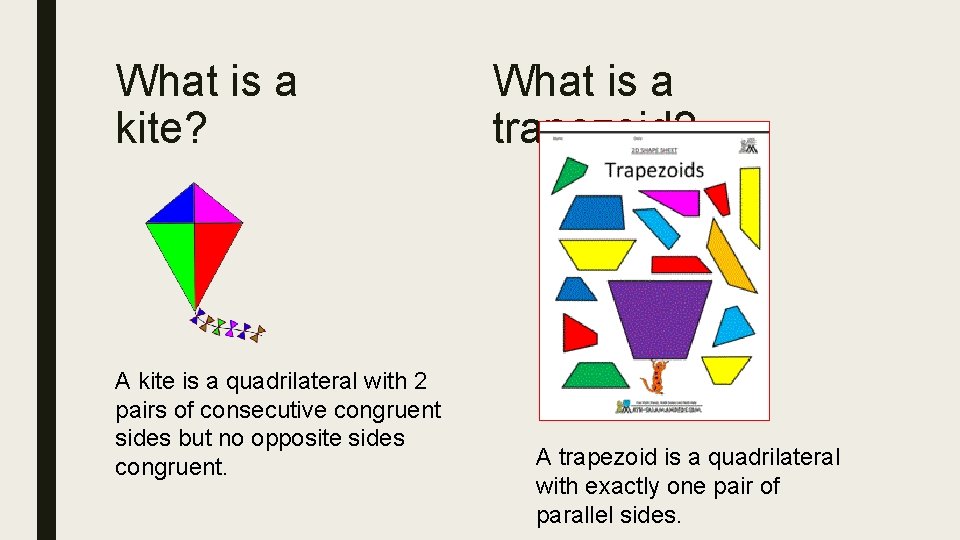
What is a kite? A kite is a quadrilateral with 2 pairs of consecutive congruent sides but no opposite sides congruent. What is a trapezoid? A trapezoid is a quadrilateral with exactly one pair of parallel sides.

Investigation 1: What are some properties of kites? ■ You will need a piece of patty paper for this investigation. ■ In this investigation, you will look at the diagonals in a kite to see what special properties they have.

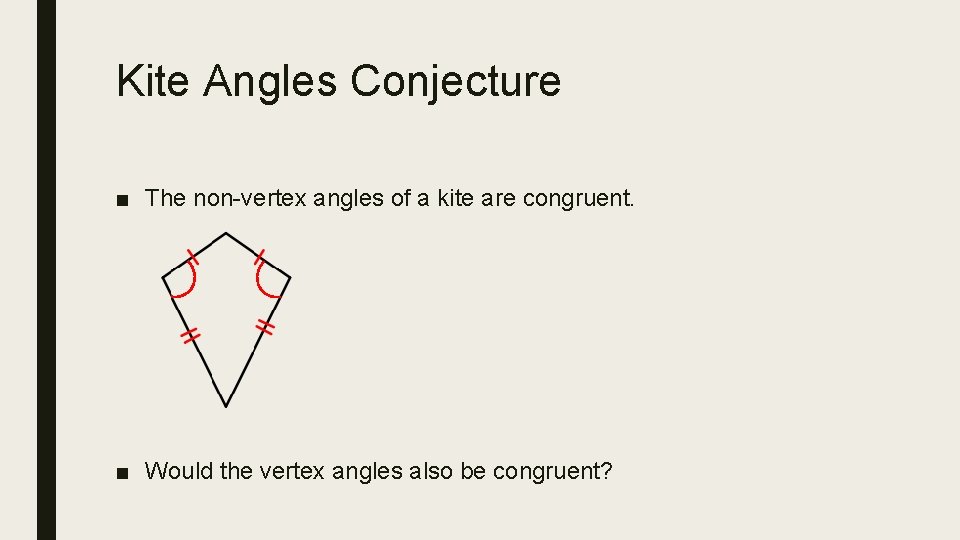
Kite Angles Conjecture ■ The non-vertex angles of a kite are congruent. ■ Would the vertex angles also be congruent?

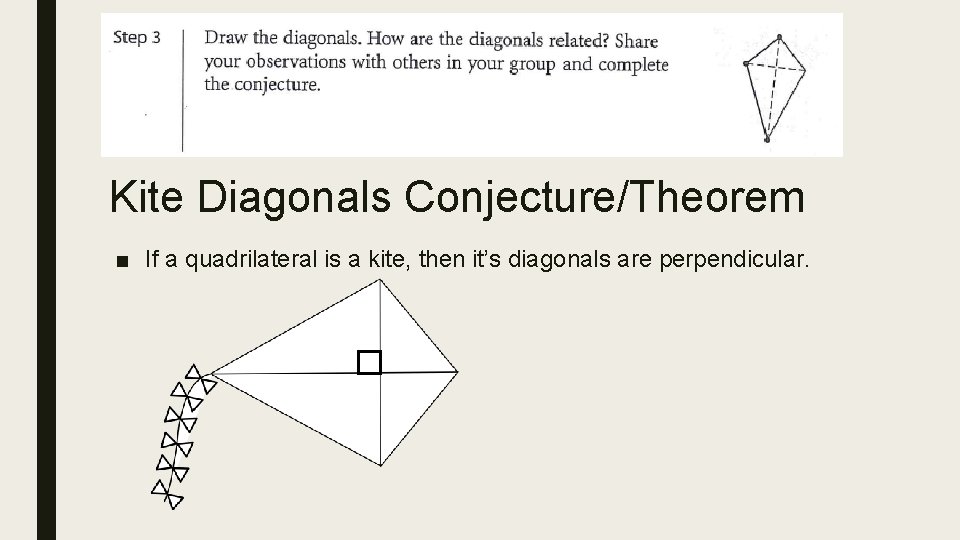
Kite Diagonals Conjecture/Theorem ■ If a quadrilateral is a kite, then it’s diagonals are perpendicular.

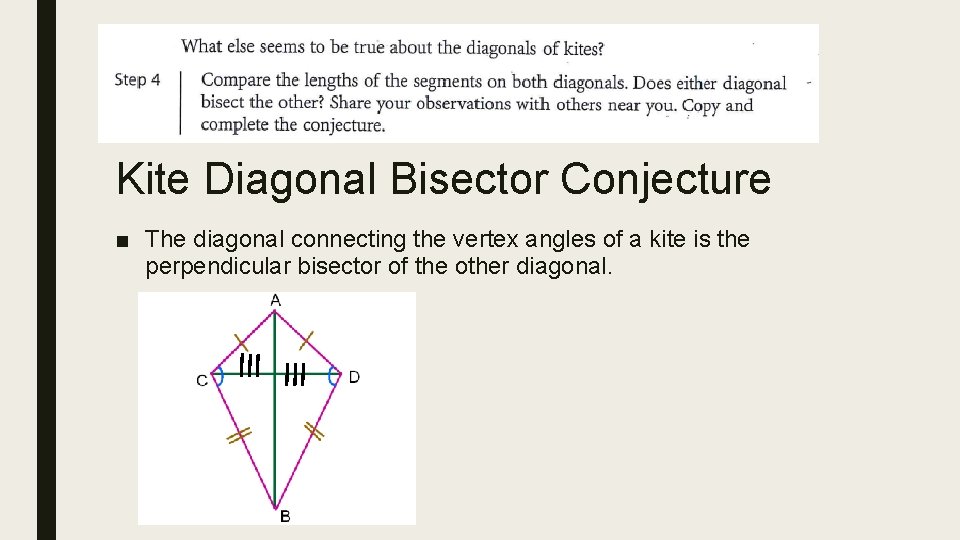
Kite Diagonal Bisector Conjecture ■ The diagonal connecting the vertex angles of a kite is the perpendicular bisector of the other diagonal.

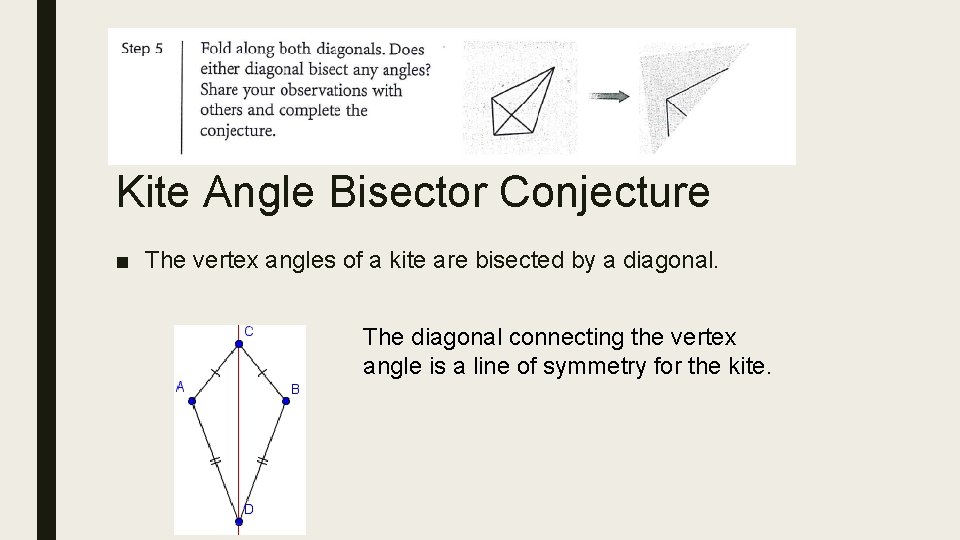
Kite Angle Bisector Conjecture ■ The vertex angles of a kite are bisected by a diagonal. The diagonal connecting the vertex angle is a line of symmetry for the kite.

Investigation 2: What are some properties of trapezoids? ■ You will need a straightedge, protractor, and compass for this investigation.

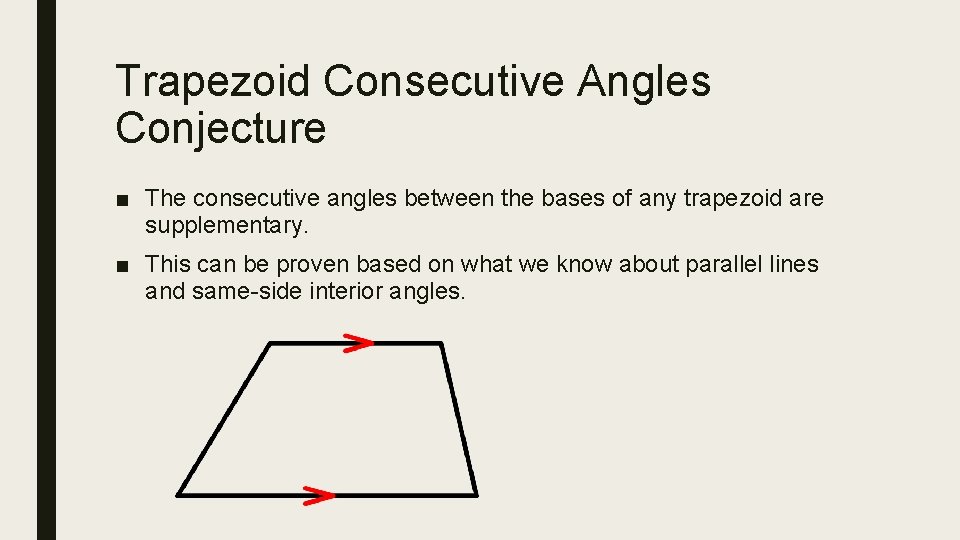
Trapezoid Consecutive Angles Conjecture ■ The consecutive angles between the bases of any trapezoid are supplementary. ■ This can be proven based on what we know about parallel lines and same-side interior angles.

Isosceles Trapezoids ■ An isosceles trapezoid is one whose non-parallel sides are congruent.

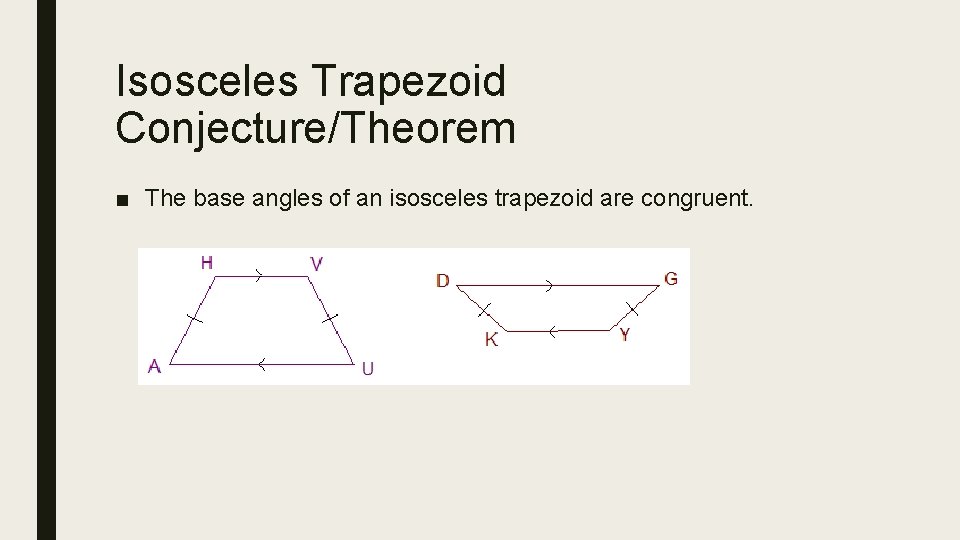
Isosceles Trapezoid Conjecture/Theorem ■ The base angles of an isosceles trapezoid are congruent.

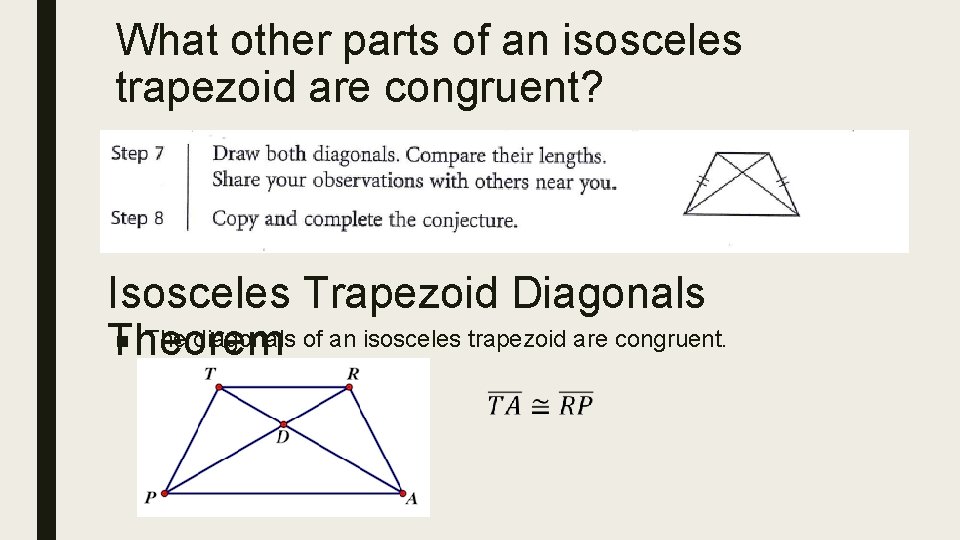
What other parts of an isosceles trapezoid are congruent? Isosceles Trapezoid Diagonals ■ The diagonals of an isosceles trapezoid are congruent. Theorem

Practice! ■ Page 394 (7 -12, 16 -25)