Entropy S Entropy is disorder or randomness 2

Entropy = S Entropy is disorder or randomness

2 nd Law of Thermodynamics Suniverse > 0 for spontaneous processes spontaneous = no external intervention Ssystem positional disorder Ssurroundings energetic disorder

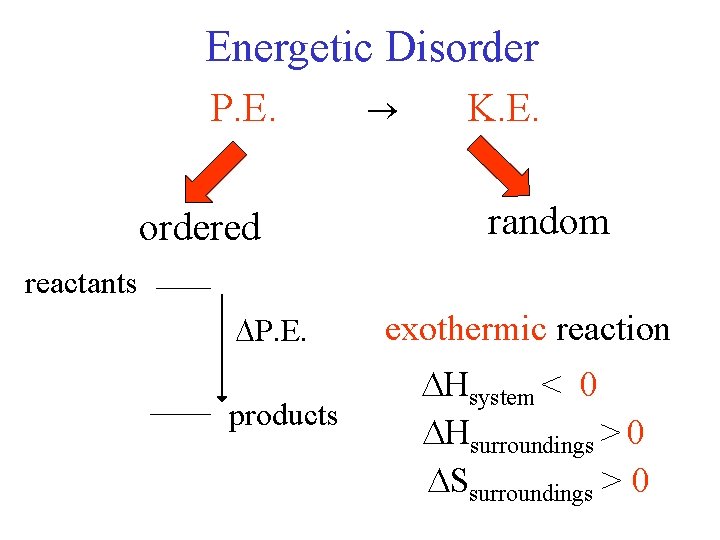
Energetic Disorder P. E. a) b) ordered reactants K. E. random a) endothermic reaction P. E. b) exothermic reaction products Hsystem < 0 Hsurroundings > 0 Ssurroundings > 0

Ssurr = - Hsystem (J/K) T Ssurr depends on T heat surroundings high T low T small effect relatively larger effect

Positional Disorder (1/2)(1/2)(1/2) = 1/64 With 1 mole of gas, Not probable

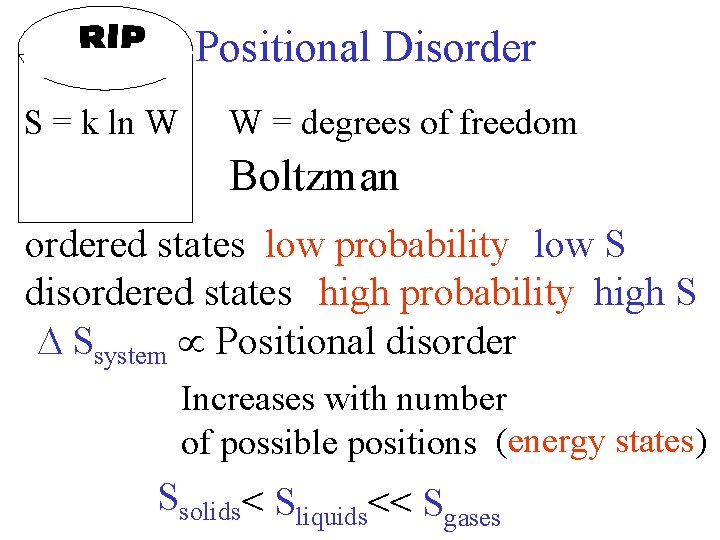
Positional Disorder S = k ln W W = degrees of freedom Boltzman ordered states low probability low S disordered states high probability high S Ssystem Positional disorder Increases with number of possible positions (energy states) Ssolids< Sliquids<< Sgases

Entropy (J/K) [heat entering system at given T] convert q to S System 1 w = -182 J q = +182 J Pext = 1. 5 atm T = 298 K System 2 Pext = 0 atm w=0 q=0 E = 0

System 3 P 1 = 6. 0 atm P 2 = 1. 5 atm V 1 = 0. 4 L V 2 = 1. 6 L T 1 = 298 K = T 2 Pext = Pint + d. P reversible process - infinitely slow V wr= - Pext d. V =- n. RT d. V = - n. RT ln (V 2/V 1) V V 2 1

Ssystem System 1 Pext = 1. 5 atm w = -182 J q = +182 J S =3. 77 J/K System 2 Pext = 0 atm w=0 q=0 S =3. 77 J/K Ssurr = - Hsystem T System 3 Pext = Pint + d. P wr = -n. RT ln (V 2/V 1) = - 1120 J qr = + 1120 J S = 3. 77 J/K Ssystem = qr = 1120 J T 298 K

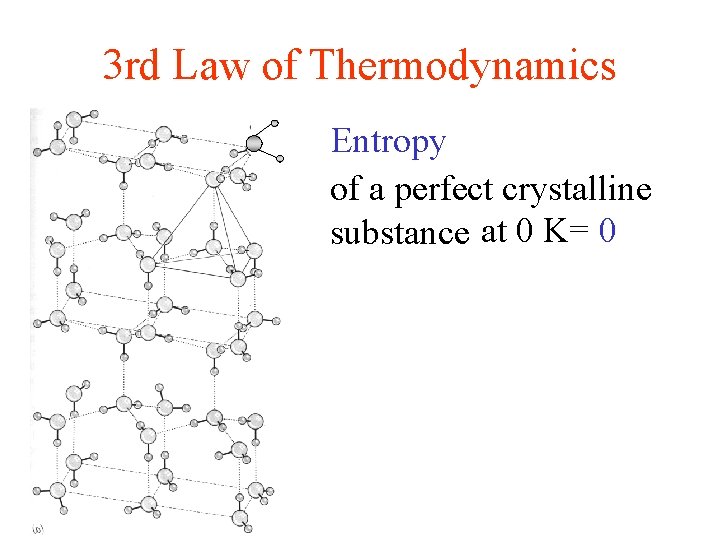
3 rd Law of Thermodynamics Entropy of a perfect crystalline substance at 0 K= 0

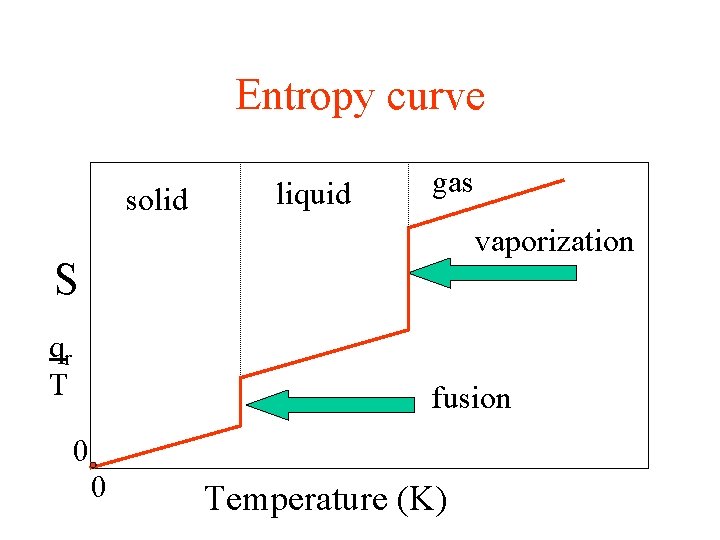
Entropy curve solid liquid gas vaporization S qr T fusion 0 0 Temperature (K)

Entropy At 0 K, S = 0 Entropy is absolute S 0 for elements in standard states S is a State Function Sorxn = n Soproducts - n Soreactants S is extensive

Increases in Entropy 1. 2. 3. 4. 5. 6. 7. Melting (fusion) Sliquid > Ssolid Vaporization Sgas >> Sliquid Increasing ngas in a reaction Heating ST 2 > ST 1 if T 2 > T 1. Dissolution ? Ssolution > (Ssolvent + Ssolute) Molecular complexity number of bonds Atomic complexity e-, protons and neutrons