Entropy Change Property diagrams Ts and hs diagrams

Entropy Change • Property diagrams (T-s and h-s diagrams) – From the definition of the entropy, it is known that Q=Td. S during a reversible process. – Hence the total heat transfer during such a process is given by Qreversible = Td. S • Therefore, it is useful to consider the T-S diagram for a reversible process involving heat transfer T On a T-S diagram, the area under the process curve represents the heat transfer for a reversible process. S

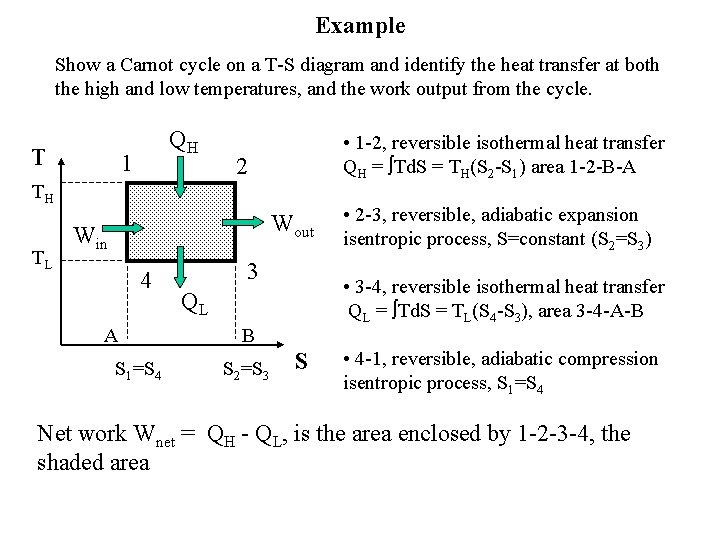
Example Show a Carnot cycle on a T-S diagram and identify the heat transfer at both the high and low temperatures, and the work output from the cycle. T QH 1 • 1 -2, reversible isothermal heat transfer QH = Td. S = TH(S 2 -S 1) area 1 -2 -B-A 2 TH TL Wout Win 4 A S 1=S 4 3 • 3 -4, reversible isothermal heat transfer QL = Td. S = TL(S 4 -S 3), area 3 -4 -A-B QL B S 2=S 3 • 2 -3, reversible, adiabatic expansion isentropic process, S=constant (S 2=S 3) S • 4 -1, reversible, adiabatic compression isentropic process, S 1=S 4 Net work Wnet = QH - QL, is the area enclosed by 1 -2 -3 -4, the shaded area

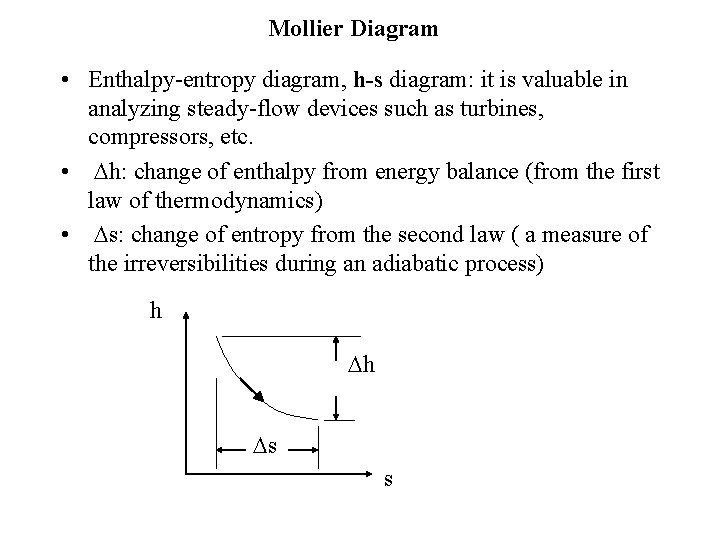
Mollier Diagram • Enthalpy-entropy diagram, h-s diagram: it is valuable in analyzing steady-flow devices such as turbines, compressors, etc. • h: change of enthalpy from energy balance (from the first law of thermodynamics) • s: change of entropy from the second law ( a measure of the irreversibilities during an adiabatic process) h h s s

Td. S (Gibbs) Equations • Since, the area under the T-s line is equal to the heat transfer for a reversible process, it would be useful to have a relationship between Temperature and Entropy to obtain the heat transfer, T. • Such a relationship exists for a closed system containing a pure, compressible substance undergoing a reversible process d. U = Qrev - Wrev = Td. S - Pd. V => Td. S = d. U + Pd. V or Tds = du + pdv ( per unit mass) • This is the well-known Gibbs equation • Alternatively, eliminate du by using the definition of enthalpy, h = u + pv => dh = du + pdv + vdp, => du + pdv = dh – vdp Td. S Tds = du + pdv Tds = dh – vdp

Comments Regarding the. Td. S Equations relate the entropy change of a system to other properties, such as enthalpy (h), internal energy (u), pressure and volume. • Hence, even though T-ds relations were derived for a reversible process, they are valid for any process, reversible or irreversible. • They are applicable for closed or open systems. • They are valid for all pure substances, single or multi-phase.

Example – Application of Tds relations • Consider steam undergoing a phase transition from liquid to vapor at a constant temperature of 20°C. Determine the entropy change sfg=sg-sf using the Gibbs equations and compare the value to that read directly from thermodynamic table. From table A-4: T=20°C, P = 2. 338 k. Pa, vf = 0. 001002(m 3/kg), vg=57. 79(m 3/kg), uf=83. 9(k. J/kg), ug=2402. 9(k. J/kg) Substituting into the Tds relation: sfg= (1/293)(2402. 9 -83. 9) + (2. 338/293)(57. 79 -0. 001002) = 8. 375(k. J/kg K) ug - uf vg - vf 1/T P/T Compares favorably with the tabulated value sfg=8. 3715(k. J/kg K)

Entropy Change of an Incompressible Substance (YAC: 6 -8) • For most liquids and all solids, the density does not change appreciably as pressure changes, hence dv 0. • Gibbs equation states that Tds = du+pdv Tds = du where du = Cd. T, for an incompressible substance and Cp=Cv=C is a function of temperature only. • Therefore, ds = du/T = C d. T/T Note: According to the above equation, an isothermal process for a pure incompressible substance is isentropic. • Specific heats for some common liquids and solids can be found in thermodynamic tables such as Table A-14 to A-18

Example – Entropy Change of Incomp. Substances A 1 -kg metal bar, initially at 1000 K, is removed from an oven and quenched by immersing in a closed tank containing 20 kg of water, initially at 300 K. Assume both substances are incompressible and Cwater= 4(k. J/kg K), Cmetal = 0. 4(k. J/kg K). Neglect heat transfer between the tank and its surroundings. (a) Determine the final temperature of the metal bar, (b) entropy generation during the process. Tm=1000 K, mm=1 kg, cm=0. 4 k. J/kg K Tw=300 K, mw=20 kg, cw=4 k. J/kg K

Solution The total entropy of the system increases, thus satisfy the second law

Entropy Change of Ideal Gases (YAC: 6 -9) From Gibbs’ equations, the change of entropy of an ideal gas can be expressed as: For an ideal gas, u=u(T) and h=h(T), du=cv(T)d. T and dh=cp(T)d. T and Pv = RT

Entropy Change of Ideal Gases – Special Cases The dependence of specific heats on temperature makes the integration more complex. However, for certain cases, one can make simplifying assumptions. Case 1: If specific heats are assumed constant, integration is simplified: Note: The above is strictly true for monatomic gases, e. g. He, Ar It is fairly accurate if the temperature difference is small. Case 2: Calculate the specific heat at an average temperature, Tavg, and assume it to be constant. This also allows the specific heat to be taken out of the integral Note: This approximation is generally fairly accurate if the temperature difference is not too large, usually good if T < few hundred degrees. Strictly speaking, one should look at the temp. dependence of specific heats for the particular substance to evaluate the validity of this approximation.

Isentropic Processes for Ideal Gases If a process is isentropic (that is adiabatic and reversible), ds = 0, s 1=s 2, then it can be shown that: The above are referred to as the: first, second and third, respectively, isentropic relations for Ideal Gases (assuming constant specific heats). They can also be written as: Tvk-1 = constant TP(1 -k)/k = constant Pvk = constant First isentropic relation Second isentropic relation Third isentropic relation

Example • Air is compressed from an initial state of 100 k. Pa and 300 K to 500 k. Pa and 360 K. Determine the entropy change using constant cp=1. 003 (k. J/kg K) • Negative entropy due to heat loss to the surroundings