Entropy and some applications in image processing Neucimar

Entropy and some applications in image processing Neucimar J. Leite Institute of Computing neucimar@ic. unicamp. br

Outline • Introduction – Intuitive understanding • Entropy as global information • Entropy as local information – edge detection, texture analysis • Entropy as minimization/maximization constraints – global thresholding – deconvolution problem

Information Entropy (Shannon´s entropy) An information theory concept closely related to the following question: - What is the minimum amount of data needed to represent an information content? • For images (compression problems): - How few data are sufficient to completely describe an images without (much) loss of information?

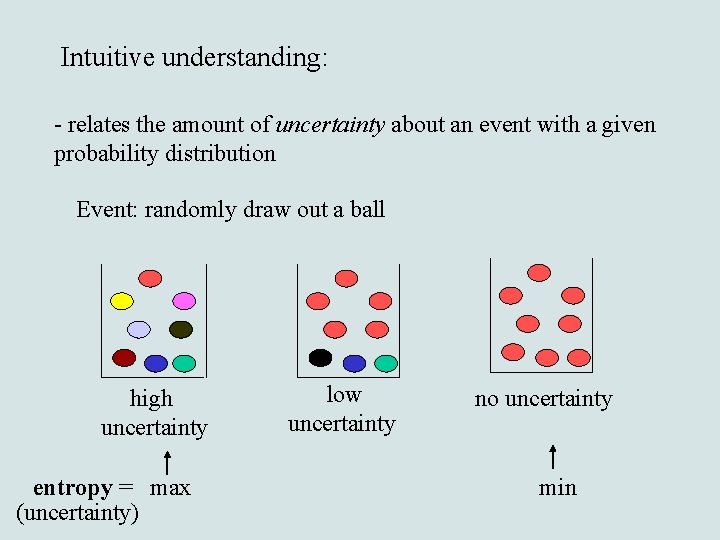
Intuitive understanding: - relates the amount of uncertainty about an event with a given probability distribution Event: randomly draw out a ball high uncertainty entropy = max (uncertainty) low uncertainty no uncertainty min

Self-information: - Units of information used to represent an event E Example 1: Event: a coin flipping = { heads, tails } Probability: P(heads) = P(tails) = 1/2 0 heads 1 tails self-information: inversely related to the probability of E

Example 2: Entropy: average information amount of conveyed information of event E

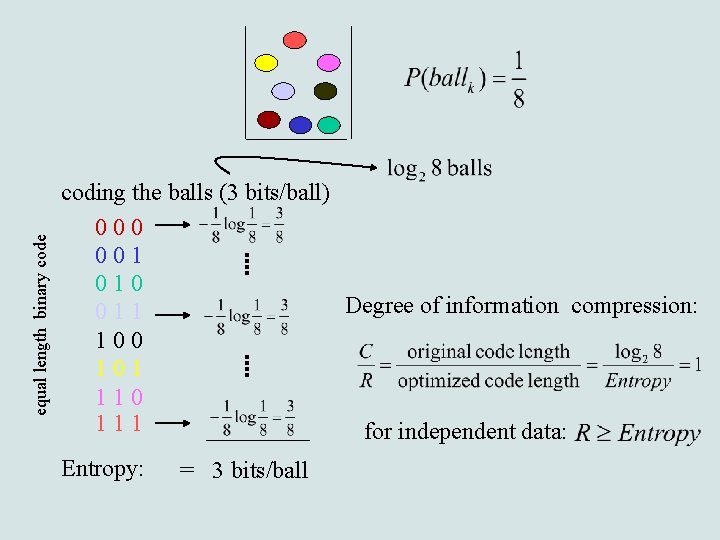
equal length binary code coding the balls (3 bits/ball) 000 001 010 Degree of information compression: 011 100 101 110 111 for independent data: Entropy: = 3 bits/ball

medium uncertainty: code 00 01 10 11 H= -( 5/8 log 2(5/8) + 1/8 log 2(1/8) ) = 1. 54 no uncertainty: H = -8 log 21 = 0

medium uncertainty: code 00 01 10 11 H= -( 5/8 log 2(5/8) + 1/8 log 2(1/8) ) = 1. 54 • 2 bits/ball > 1. 54 bit/ball and code redundancy !!! 22% We need an encoding method for eliminating this code redundancy

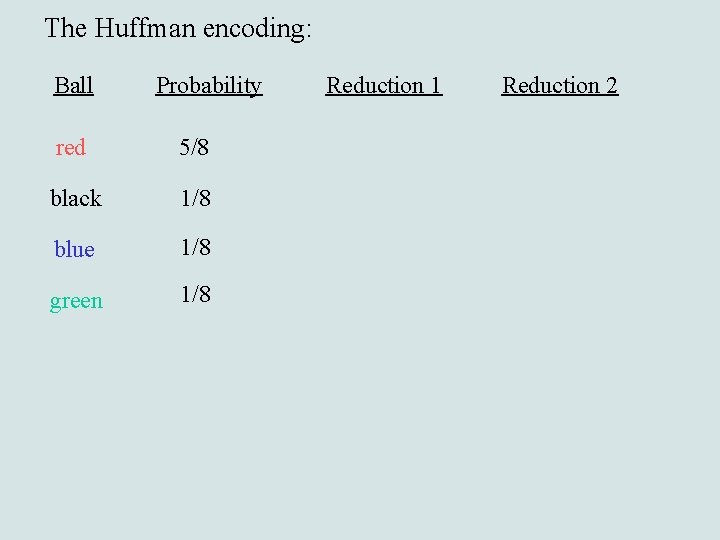
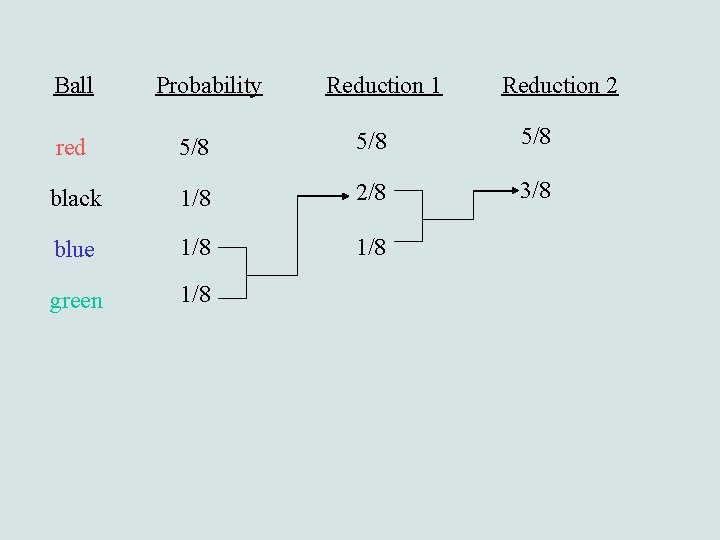
The Huffman encoding: Ball Probability red 5/8 black 1/8 blue 1/8 green 1/8 Reduction 1 Reduction 2

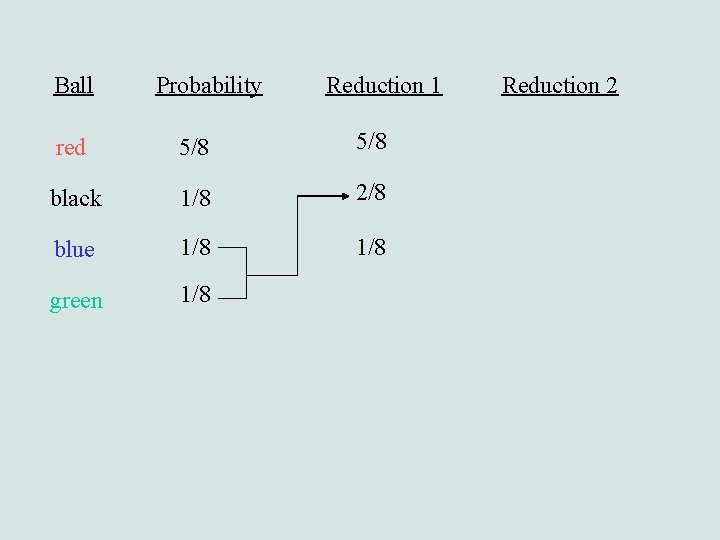
Ball Probability Reduction 1 red 5/8 black 1/8 2/8 blue 1/8 green 1/8 Reduction 2

Ball Probability Reduction 1 Reduction 2 red 5/8 5/8 black 1/8 2/8 3/8 blue 1/8 green 1/8

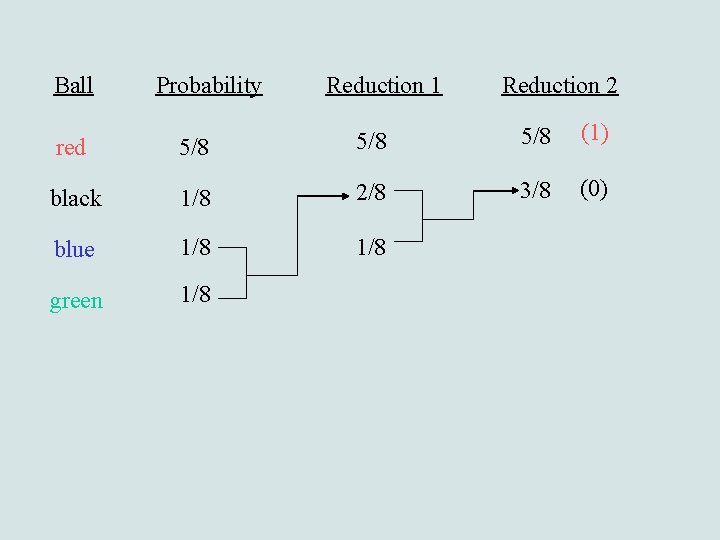
Ball Probability Reduction 1 red 5/8 black 1/8 2/8 blue 1/8 green 1/8 Reduction 2 5/8 (1) 3/8 (0)

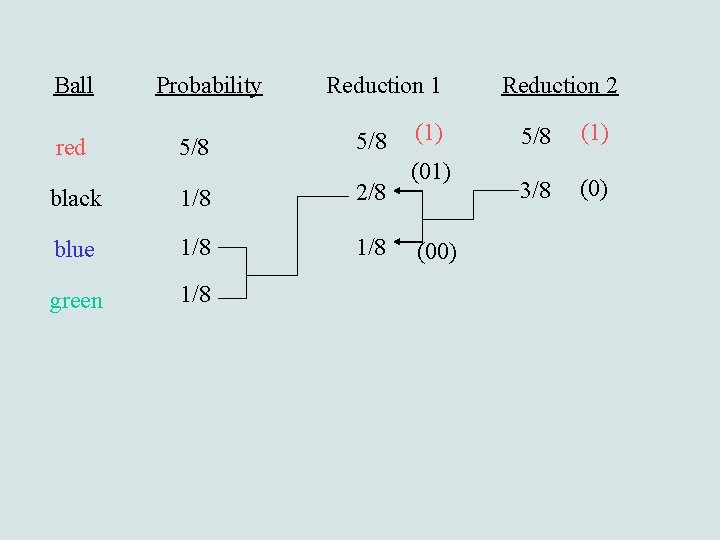
Ball Probability Reduction 1 red 5/8 black 1/8 2/8 blue 1/8 green 1/8 (1) (00) Reduction 2 5/8 (1) 3/8 (0)

Ball Probability red 5/8 (1) black 1/8 (00) blue 1/8 green 1/8 ball red black blue green Reduction 1 (011) 5/8 2/8 1/8 (1) (01) Reduction 2 5/8 (1) 3/8 (0) (010) variable length code 1 00 011 010 and (18, 6%)

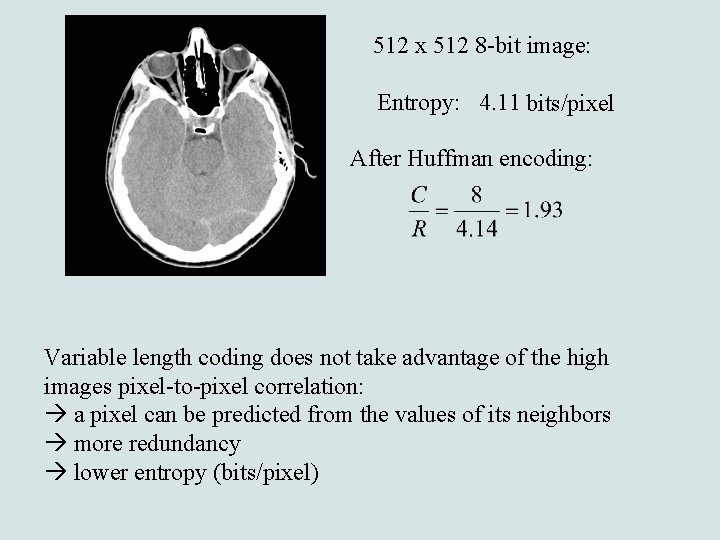
512 x 512 8 -bit image: Entropy: 4. 11 bits/pixel After Huffman encoding: Variable length coding does not take advantage of the high images pixel-to-pixel correlation: a pixel can be predicted from the values of its neighbors more redundancy lower entropy (bits/pixel)

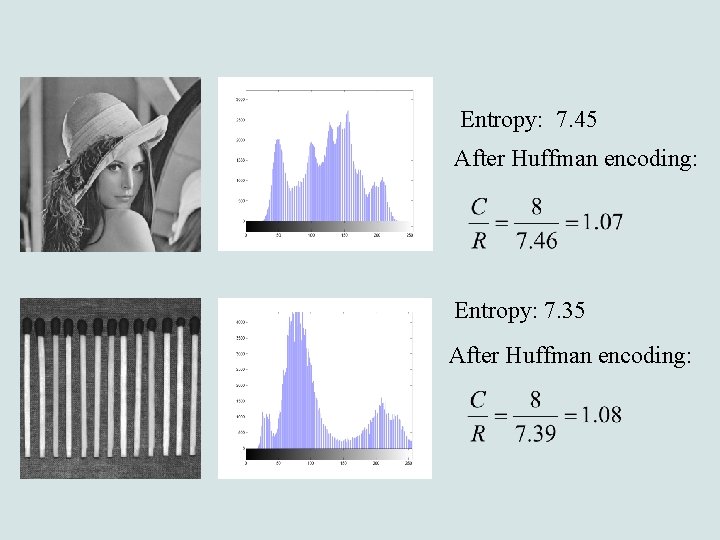
Entropy: 7. 45 After Huffman encoding: Entropy: 7. 35 After Huffman encoding:

Coding the interpixel difference highlighting redundancies: Entropy: 4. 73 instead of 7. 45 After Huffman encoding: instead of 1. 07 Entropy: 5. 97 instead of 7. 35 After Huffman encoding: instead of 1. 08

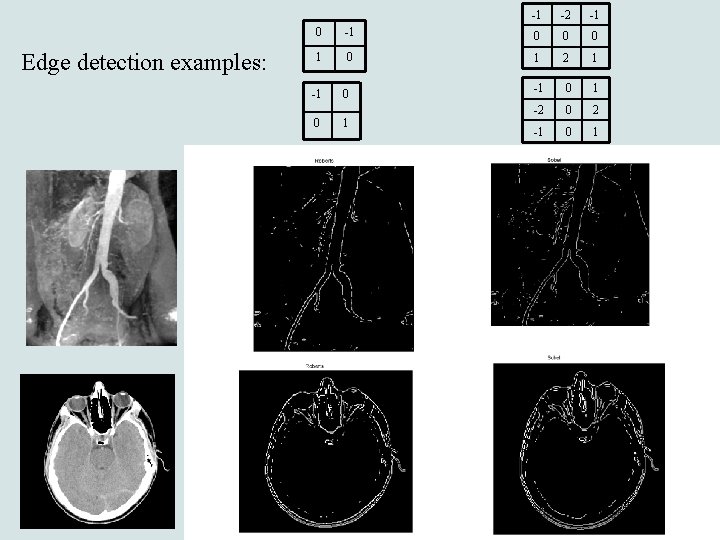
Entropy as a local information: the edge detection example

Edge detection examples: -1 -2 -1 0 0 0 1 2 1 -1 0 1 -2 0 2 -1 0 1 -1 0 0 1

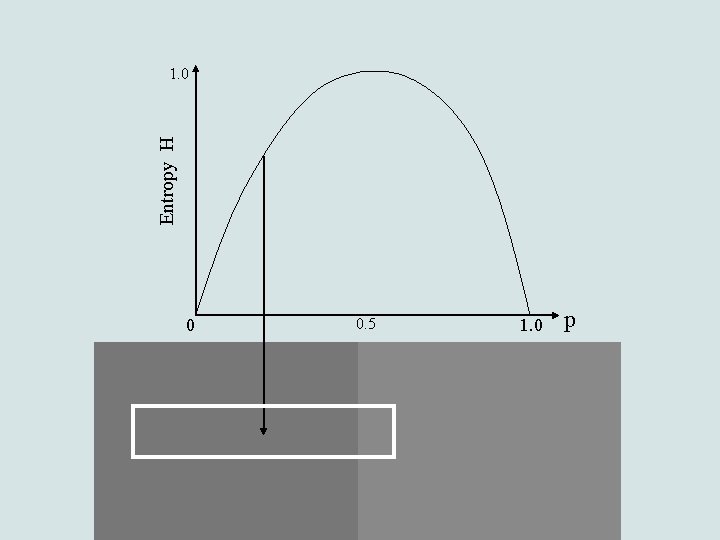
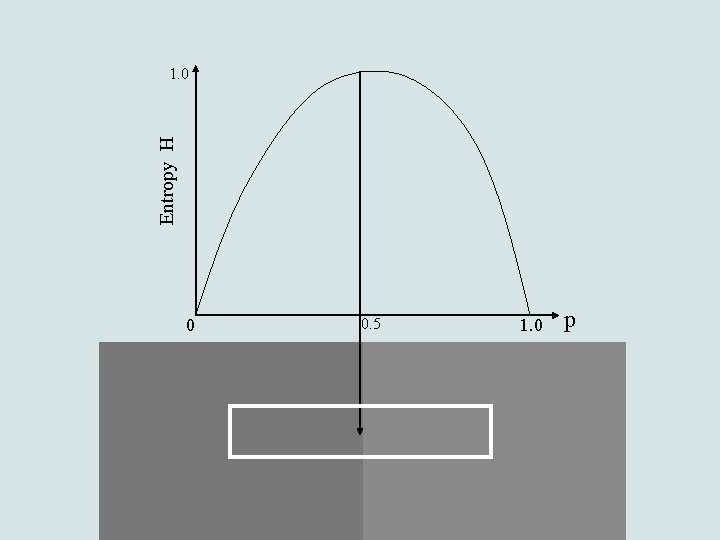
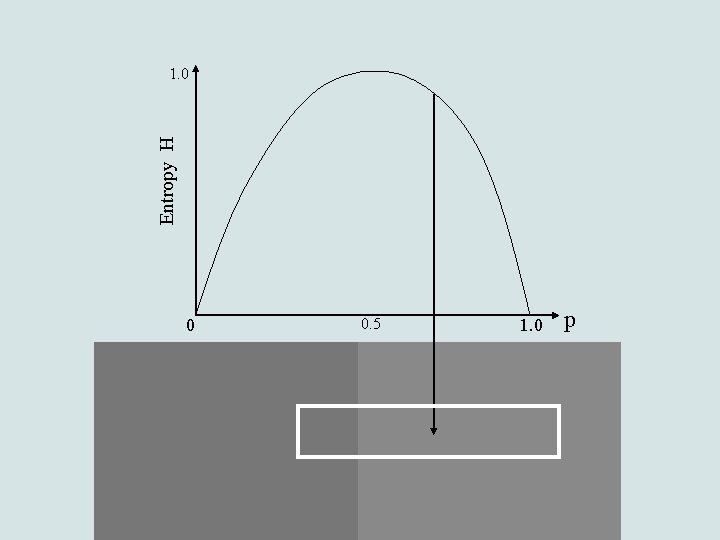
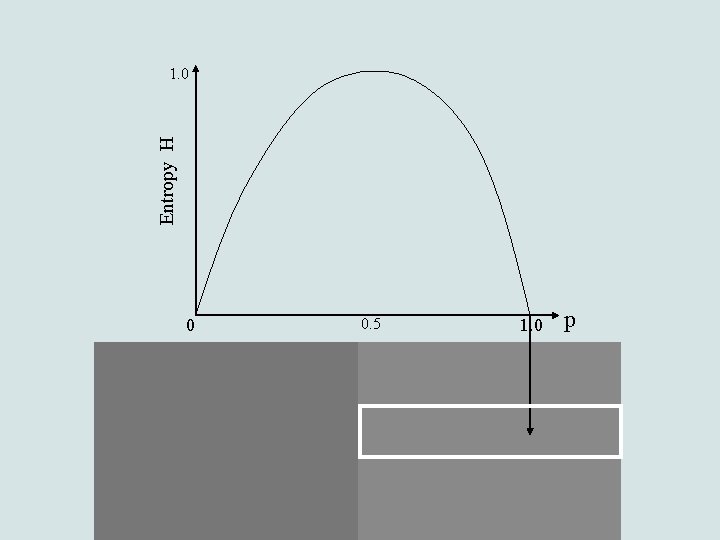
Entropy-based edge detection • Low entropy values low frequencies uniform image regions • High entropy values high frequencies image edges

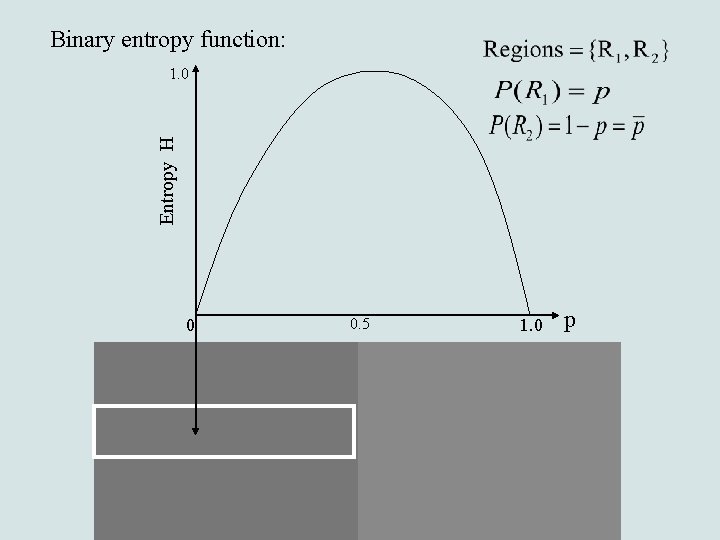
Binary entropy function: Entropy H 1. 0 0 0. 5 1. 0 p

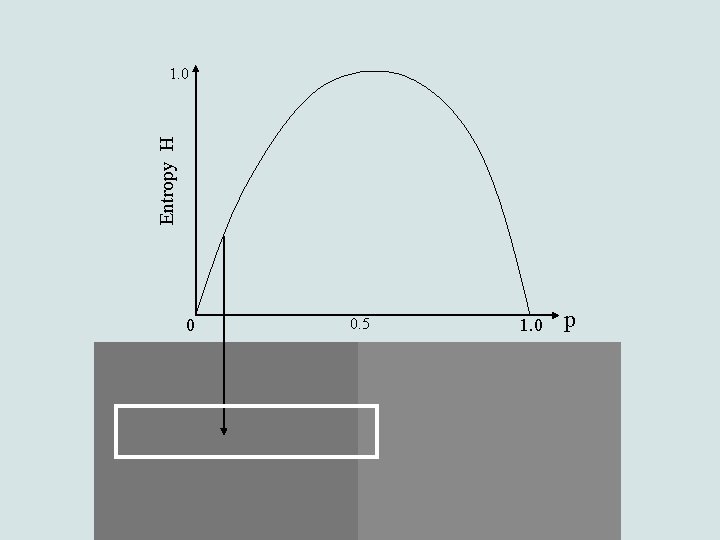
Entropy H 1. 0 0 0. 5 1. 0 p

Entropy H 1. 0 0 0. 5 1. 0 p

Entropy H 1. 0 0 0. 5 1. 0 p

Entropy H 1. 0 0 0. 5 1. 0 p

Entropy H 1. 0 0 0. 5 1. 0 p

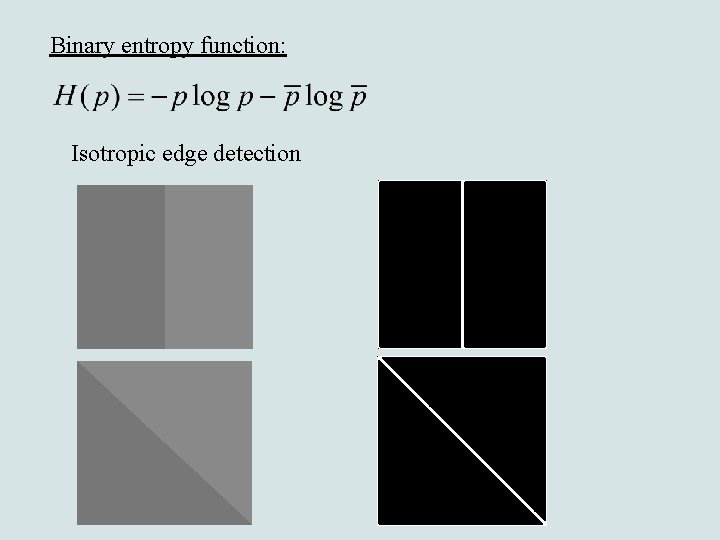
Binary entropy function: Isotropic edge detection

H in a 3 x 3 neighborhood:

5 x 5 neighborhood:

7 x 7 neighborhood:

9 x 9 neighborhood:

Texture Analysis • Similarity grouping based on brightness, colors, slopes, sizes etc • The perceived patterns of lightness, directionality, coarseness, regularity, etc can be used to describe and segment an image

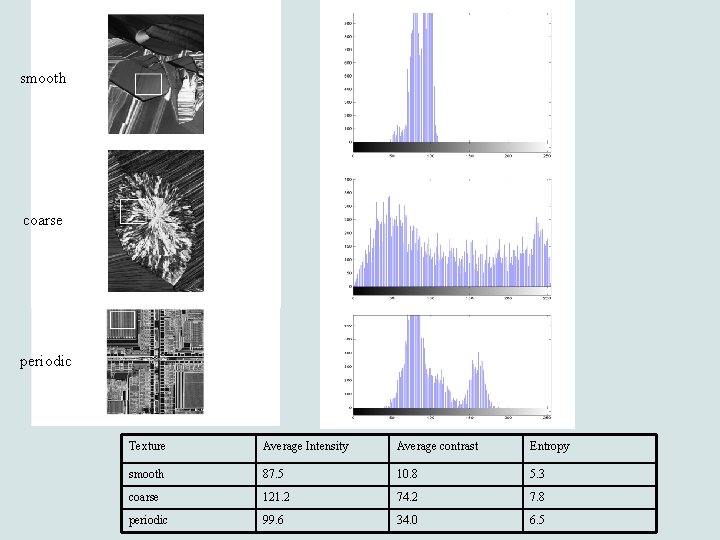
Texture description: statistical approach • Characterizes textures as smooth, coarse, periodic, etc - Based on the intensity histogram prob. density function Descriptors examples: • Mean: a measure of average intensity p(zi) = the intensity histogram in a region zi = random variable denoting gray levels

• Other moments of different orders: - e. g. , standard deviation: a measure of average contrast Entropy: a measure of randomness

smooth coarse periodic Texture Average Intensity Average contrast Entropy smooth 87. 5 10. 8 5. 3 coarse 121. 2 74. 2 7. 8 periodic 99. 6 34. 0 6. 5

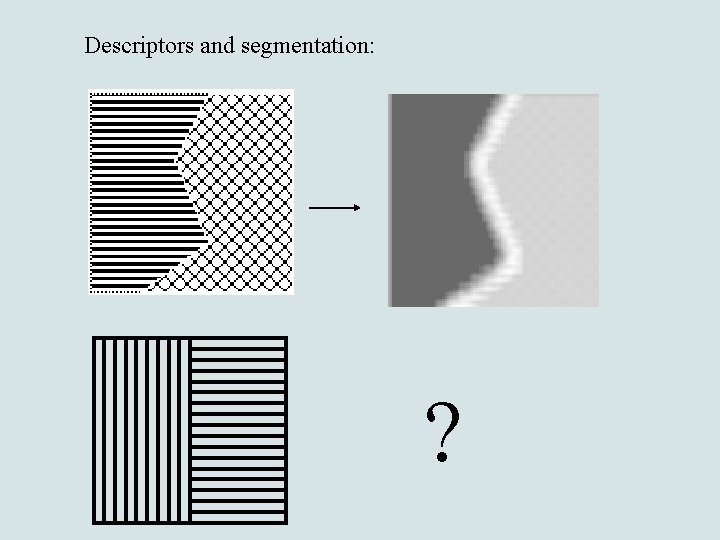
Descriptors and segmentation: ?

Gray-level co-occurrence matrix: Haralick´s descriptors • Conveys information about the positions of pixels having similar gray level values. Md(a, b) 1 d=1 2 3 3 3 1 2 2 1 3 2 2 2 3 2 1 1 1 1 1 3 3 0 1 2 3 4 0 0 0 4 3 1 0 0 2 3 2 0 0 1 2 3 0 0 0

Md = the probability that a pixel with gray level i will have a pixel with level j a distance of d pixels away in a given direction For the descriptor H: large empty spaces in M little information content cluttered areas large information content d = 2, horizontal direction

Obviously, more complex texture analysis based on statistical descriptors should consider combination of information related to image scale, moments, contrast, homogeneity, directionality, etc

Entropy as minimization/maximization constraints

Global thresholding examples: mean histogram peaks

For images with levels 0 -255: The probability that a given pixel will have value less than or equal t is: Now considering: Class A: Class B:

The optimal threshold is the value of t that maximizes where

Examples:

Entropy as a fuzziness measure In fuzzy set theory an element x belongs to a set S with a certain probability px defined by a membership function px(x) Example of a membership function for a given threshold t: px(x) gives the degree to which x belongs to the object or background with gray-level average and , respectively.

How can the degree of fuzziness be measured? Example: t = 0 for a a binary image fuzziness = 0

Using the Shannon´s function (for two classes): the entropy of an entire fuzzy set of dimension Mx. N is and for segmentation purpose, the threshold t is such that E(t) is minimum t minimizes fuzziness

Segmentation examples

Maximum Entropy Restoration: the deconvolution problem

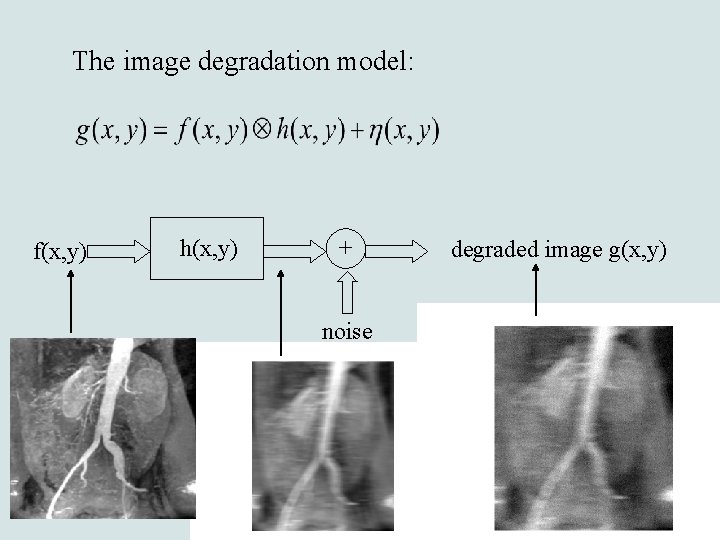
The image degradation model: f(x, y) h(x, y) + noise degraded image g(x, y)

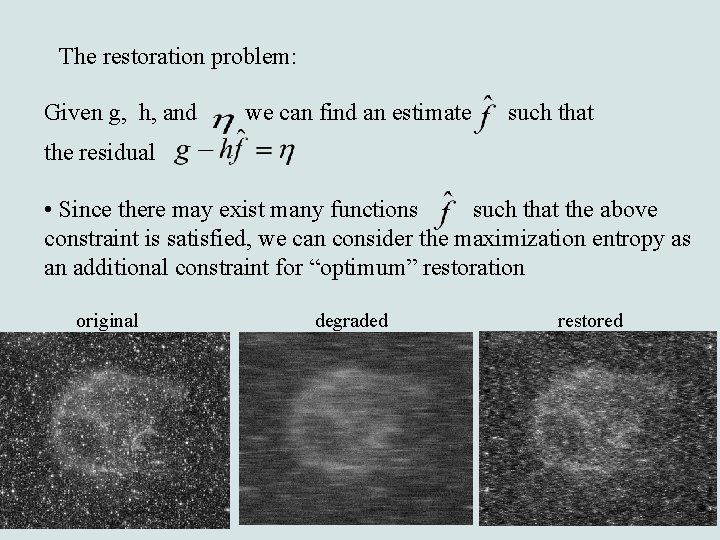
The restoration problem: Given g, h, and we can find an estimate such that the residual • Since there may exist many functions such that the above constraint is satisfied, we can consider the maximization entropy as an additional constraint for “optimum” restoration original degraded restored

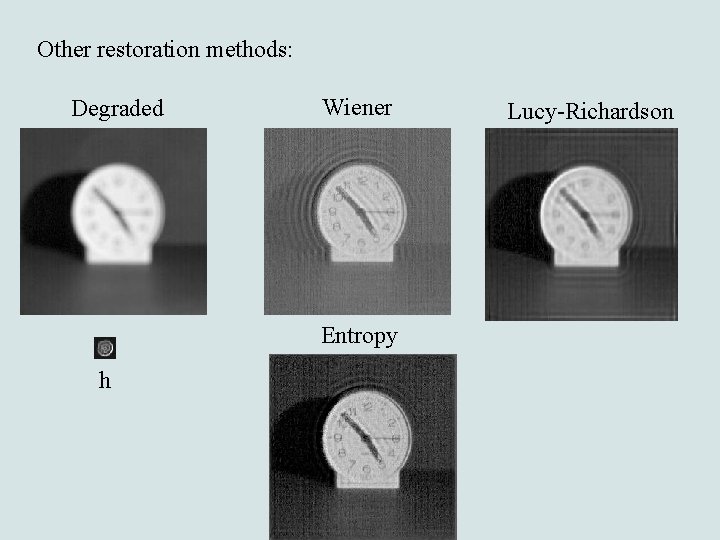
Other restoration methods: Degraded Wiener Entropy h Lucy-Richardson

Conclusions • The entropy information has been extensively used in various image processing applications. • Other examples concern distortion prediction, images evaluation, registration, multiscale analysis, high-level feature extraction and classification, etc