Entropy and entanglement on the horizon Danny Terno

Entropy and entanglement on the horizon Danny Terno joint work with Etera Livine gr-qc/0508085 gr-qc/0505068 Phys. Rev. A 72 022307 (2005)

Black hole in LQG Object: static black hole Comment 1: no dynamics Comment 2: closed 2 -surface States: spin network that crosses the horizon Definition of a “black hole”: complete coarse-graining of the spin network inside Gauge invariance: SU(2) invariance at each vertex becomes SU(2) invariance for the horizon states Microscopic states: intertwiners

Features & assumptions Area spectrum The probing scale We work at fixed j Comment: reasons to be discussed The flow: scaling and invariance of physical quantities For starters: a qubit black hole

Summary Qubit black hole Spin-j black hole Entanglement between halves of the horizon Logarithmic correction = quantum mutual information Area rescaling

Standard counting story area constraint number of states entropy Fancy counting story density matrix entropy 2 n spins

Combinatorics Schur’s duality is the irrep of the permutation group Example: =#standard tableaux 1 2 1 3 3 4 2 4

Entanglement a brief history Ancient times: 1935 -1993 “The sole use of entanglement was to subtly humiliate the opponents of QM” Modern age: 1993 Resource of QIT Teleportation, quantum dense coding, quantum computation…. Postmodern age: 1986 (2001)Entanglement in physics 1/3

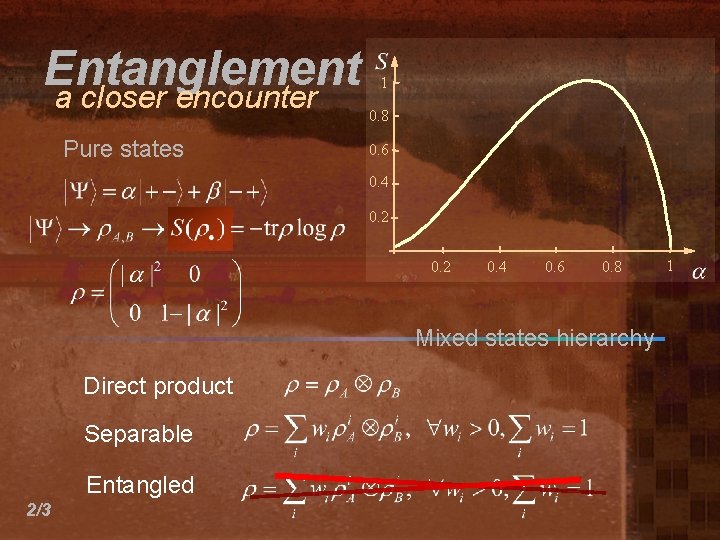
Entanglement a closer encounter Pure states 1 0. 8 0. 6 0. 4 0. 2 0. 4 0. 6 0. 8 Mixed states hierarchy Direct product Separable Entangled 2/3 1

Entanglement measures Entanglement of formation Minimal weighted average entanglement of constituents n w o n “Good” measures of entanglement: satisfy three axioms k r e v e n t s o m l A Coincide on pure states with Zero on unentangled states 3/3 Do not increase under LOCC

Entanglement calculation Clever notation

Entanglement 2 vs 2 n-2 States degeneracy indices Unentangled fraction Entanglement

n vs n Entropy of the whole vs. sum of its parts Reduced density matrices BH is not made from independent qubits, but… Logarithmic correction equals quantum mutual information

Why qubits (fixed j)? Answer 1: Dreyer, Markopoulou, Smolin Comment: spin-1 Answer 2: if the spectrum is Decomposition into spin-1/2. 1 -1 relation between the intertwiners. No area change Answer 3: irreducibility

Universality and the random walks Entropy Explanation: a random walk with a mirror Practical calculation: -4 -2 -1 -3 RWM(0)=RW(0)-RW(1) 1 2 3 4

Calculations & asymptotics Asymptotics Entanglement: n vs n

Area renormalization Generic surface, 2 n qubits Complete coarse-graining The most probable spin: maximal degeneracy Horizon, 2 n qubits split into p patches of 2 k qubits

different options The most probable spin: maximal degeneracy The average spin: Area rescaling:

Open questions

Open questions Dynamics: evolution of entanglement dynamical evolution of evaporation "H=0" section & the number of states Semi-classicality: requiring states to represent semi-classical BH rotating BH

Evaporation A model for Bekenstein-Mukhanov spectroscopy (1995) Minimal frequency <= fundamental j Probability for the jump is proportional to the unentangled fraction (of 2 -spin blocks) number of blocks

Entanglement calculation Clever notation (2): Clever notation (3): Coup de grâce: • Alternative decomposition: linear combinations • Its reduced density matrices: mixtures • Entropy: concavity