ENTHALPY CHANGES ENTHALPY CHANGES CONTENTS Thermodynamics Enthalpy changes























- Slides: 34

ENTHALPY CHANGES

ENTHALPY CHANGES CONTENTS • Thermodynamics • Enthalpy changes • Standard enthalpy values • Standard enthalpy of formation • Standard enthalpy of combustion • Enthalpy of neutralisation • Bond dissociation enthalpy • Hess’s law • Calculating enthalpy changes using bond enthalpies • Calculating enthalpy changes using enthalpy of formation values • Calculating enthalpy changes using enthalpy of combustion values • Practical measurement • Check list

ENTHALPY CHANGES Before you start it would be helpful to… • be able to balance equations • be confident with simple arithmetical operations

THERMODYNAMICS First Law Energy changes Examples Energy can be neither created nor destroyed but It can be converted from one form to another all chemical reactions are accompanied by some form of energy changes can be very obvious (e. g. coal burning) but can go unnoticed Exothermic Energy is given out Endothermic Energy is absorbed Exothermic combustion of fuels respiration (oxidation of carbohydrates) Endothermic photosynthesis thermal decomposition of calcium carbonate

THERMODYNAMICS - ENTHALPY CHANGES Enthalpy a measure of the heat content of a substance at constant pressure you cannot measure the actual enthalpy of a substance you can measure an enthalpy CHANGE written as the symbol DH , “delta H ” Enthalpy change (DH) = Enthalpy of products - Enthalpy of reactants

THERMODYNAMICS - ENTHALPY CHANGES a measure of the heat content of a substance at constant pressure you cannot measure the actual enthalpy of a substance you can measure an enthalpy CHANGE written as the symbol DH , “delta H ” Enthalpy change (DH) = Enthalpy of products - Enthalpy of reactants ENTHALPY Enthalpy REACTION CO-ORDINATE Enthalpy of reactants > products DH = - ive EXOTHERMIC Heat given out

THERMODYNAMICS - ENTHALPY CHANGES a measure of the heat content of a substance at constant pressure you cannot measure the actual enthalpy of a substance you can measure an enthalpy CHANGE written as the symbol DH , “delta H ” ENTHALPY Enthalpy change (DH) = Enthalpy of products - Enthalpy of reactants ENTHALPY Enthalpy REACTION CO-ORDINATE Enthalpy of reactants > products DH = - ive EXOTHERMIC Heat given out REACTION CO-ORDINATE Enthalpy of reactants < products DH = + ive ENDOTHERMIC Heat absorbed

STANDARD ENTHALPY CHANGES Why a standard? enthalpy values vary according to the conditions a substance under these conditions is said to be in its standard state. . . Pressure: A stated temperature 100 k. Pa (1 atmosphere) usually 298 K (25°C) • as a guide, just think of how a substance would be under normal lab conditions • assign the correct subscript [(g), (l) or (s) ] to indicate which state it is in • any solutions are of concentration 1 mol dm-3 • to tell if standard conditions are used we modify the symbol for DH. Enthalpy Change Standard Enthalpy Change (at 298 K)

STANDARD ENTHALPY OF FORMATION Definition The enthalpy change when ONE MOLE of a compound is formed in its standard state from its elements in their standard states. Symbol DH°f Values Usually, but not exclusively, exothermic Example(s) C(graphite) + O 2(g) ———> CO 2(g) H 2(g) + ½O 2(g) ———> 2 C(graphite) + ½O 2(g) + Notes H 2 O(l) 3 H 2(g) ———> C 2 H 5 OH(l) Only ONE MOLE of product on the RHS of the equation Elements In their standard states have zero enthalpy of formation. Carbon is usually taken as the graphite allotrope.

STANDARD ENTHALPY OF COMBUSTION Definition The enthalpy change when ONE MOLE of a substance undergoes complete combustion under standard conditions. All reactants and products are in their standard states. Symbol DH°c Values Always exothermic Example(s) C(graphite) + O 2(g) ———> CO 2(g) H 2(g) + ½O 2(g) ———> H 2 O(l) C 2 H 5 OH(l) + 3 O 2(g) ———> 2 CO 2(g) + 3 H 2 O(l) Notes Always only ONE MOLE of what you are burning on the LHS of the equation To aid balancing the equation, remember. . . you get one carbon dioxide molecule for every carbon atom in the original and one water molecule for every two hydrogen atoms When you have done this, go back and balance the oxygen.

ENTHALPY OF NEUTRALISATION Definition The enthalpy change when ONE MOLE of water is formed from its ions in dilute solution. Values Exothermic Equation H+(aq) Notes A value of -57 k. J mol-1 is obtained when strong acids react with strong alkalis. + OH¯(aq) ———> H 2 O(l) See later slides for practical details of measurement

BOND DISSOCIATION ENTHALPY Definition Energy required to break ONE MOLE of gaseous bonds to form gaseous atoms. Values Endothermic - Energy must be put in to break any chemical bond Examples Cl 2(g) Notes • • ———> 2 Cl(g) O-H(g) ———> O(g) + H(g) strength of bonds also depends on environment; MEAN values quoted making bonds is exothermic as it is the opposite of breaking a bond for diatomic gases, bond enthalpy = 2 x enthalpy of atomisation smaller bond enthalpy = weaker bond = easier to break

BOND DISSOCIATION ENTHALPY Definition Energy required to break ONE MOLE of gaseous bonds to form gaseous atoms. Values Endothermic - Energy must be put in to break any chemical bond Examples Cl 2(g) Notes • • ———> 2 Cl(g) O-H(g) ———> O(g) + H(g) strength of bonds also depends on environment; MEAN values quoted making bonds is exothermic as it is the opposite of breaking a bond for diatomic gases, bond enthalpy = 2 x enthalpy of atomisation smaller bond enthalpy = weaker bond = easier to break Mean Values Average (mean) values are quoted because the actual value depends on the environment of the bond i. e. where it is in the molecule H-H C-C C=C C C C-O C=O C-H C-N C-F C-Cl 436 346 611 837 360 743 413 305 484 338 H-F H-Cl H-Br H-I H-N H-O H-Si P-H O-O 562 431 366 299 388 463 338 318 322 146 UNITS = k. J mol-1 N-N N=N N N P-P F-F Cl-Cl Br-Br I-I S-S Si-Si 163 409 944 172 158 242 193 151 264 176

HESS’S LAW “The enthalpy change is independent of the path taken provided that the starting and end conditions are exactly the same” How The enthalpy change going from A to B can be found by adding the values of the enthalpy changes for the reactions A to X, X to Y and Y to B. DHr = DH 1 + DH 2 + DH 3

HESS’S LAW “The enthalpy change is independent of the path taken provided that the starting and end conditions are exactly the same” How The enthalpy change going from A to B can be found by adding the values of the enthalpy changes for the reactions A to X, X to Y and Y to B. DHr = DH 1 + DH 2 + DH 3 If you go in the opposite direction of an arrow, you subtract the value of the enthalpy change. e. g. DH 2 = - DH 1 + DHr - DH 3 The values of DH 1 and DH 3 have been subtracted because the route involves going in the opposite direction to their definition.

HESS’S LAW “The enthalpy change is independent of the path taken provided that the starting and end conditions are exactly the same” Use applying Hess’s Law enables one to calculate enthalpy changes from other data, such as. . . changes which cannot be measured directly e. g. Lattice Enthalpy enthalpy change of reaction from bond enthalpy change of reaction from DH°c enthalpy change of formation from DH°f

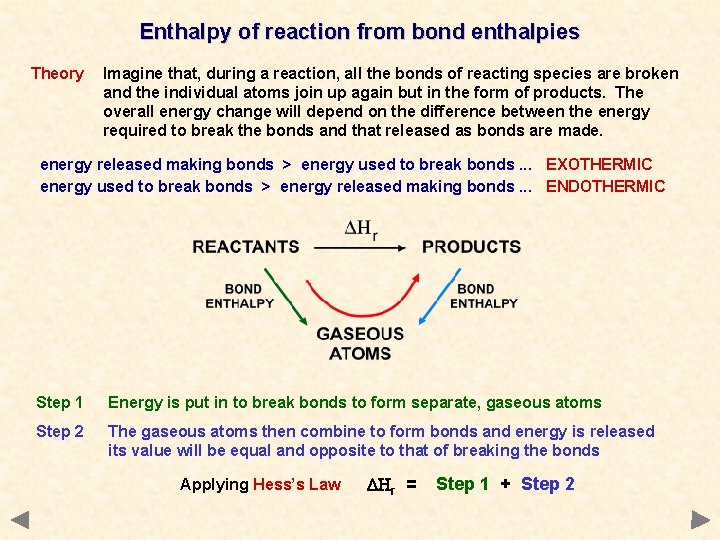
Enthalpy of reaction from bond enthalpies Theory Imagine that, during a reaction, all the bonds of reacting species are broken and the individual atoms join up again but in the form of products. The overall energy change will depend on the difference between the energy required to break the bonds and that released as bonds are made. energy released making bonds > energy used to break bonds. . . EXOTHERMIC energy used to break bonds > energy released making bonds. . . ENDOTHERMIC Step 1 Energy is put in to break bonds to form separate, gaseous atoms Step 2 The gaseous atoms then combine to form bonds and energy is released its value will be equal and opposite to that of breaking the bonds Applying Hess’s Law DHr = Step 1 + Step 2

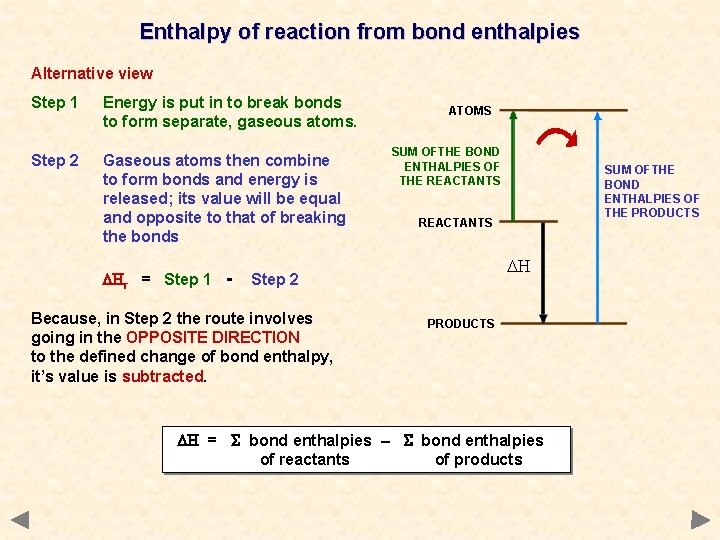
Enthalpy of reaction from bond enthalpies Alternative view Step 1 Energy is put in to break bonds to form separate, gaseous atoms. Step 2 Gaseous atoms then combine to form bonds and energy is released; its value will be equal and opposite to that of breaking the bonds DHr = Step 1 - ATOMS SUM OFTHE BOND ENTHALPIES OF THE REACTANTS DH Step 2 Because, in Step 2 the route involves going in the OPPOSITE DIRECTION to the defined change of bond enthalpy, it’s value is subtracted. SUM OFTHE BOND ENTHALPIES OF THE PRODUCTS DH = bond enthalpies – bond enthalpies of reactants of products

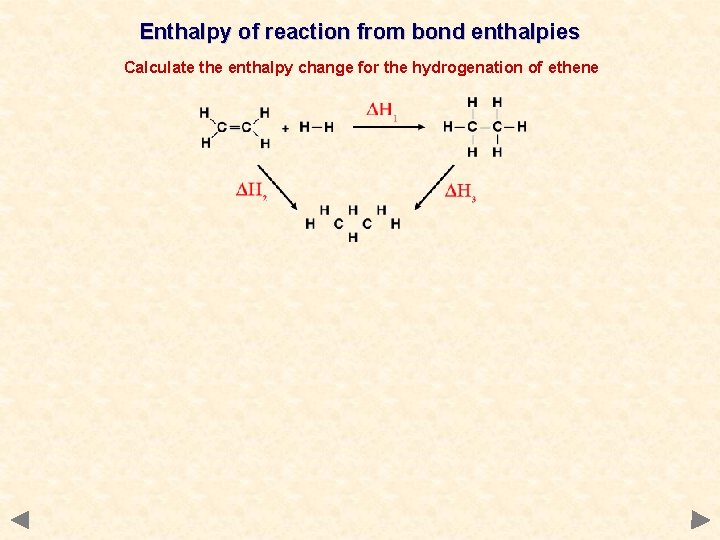
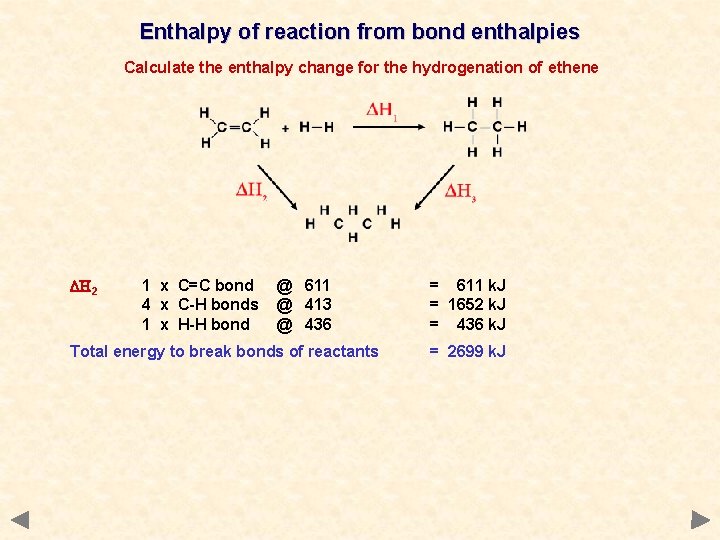
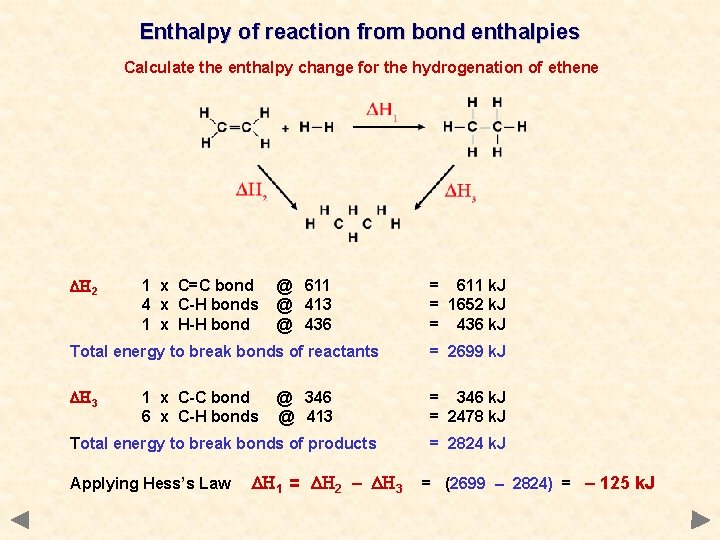
Enthalpy of reaction from bond enthalpies Calculate the enthalpy change for the hydrogenation of ethene

Enthalpy of reaction from bond enthalpies Calculate the enthalpy change for the hydrogenation of ethene DH 2 1 x C=C bond 4 x C-H bonds 1 x H-H bond @ 611 @ 413 @ 436 Total energy to break bonds of reactants = 611 k. J = 1652 k. J = 436 k. J = 2699 k. J

Enthalpy of reaction from bond enthalpies Calculate the enthalpy change for the hydrogenation of ethene DH 2 1 x C=C bond 4 x C-H bonds 1 x H-H bond @ 611 @ 413 @ 436 = 611 k. J = 1652 k. J = 436 k. J Total energy to break bonds of reactants = 2699 k. J DH 3 = 346 k. J = 2478 k. J 1 x C-C bond 6 x C-H bonds @ 346 @ 413 Total energy to break bonds of products Applying Hess’s Law DH 1 = DH 2 – DH 3 = 2824 k. J = (2699 – 2824) = – 125 k. J

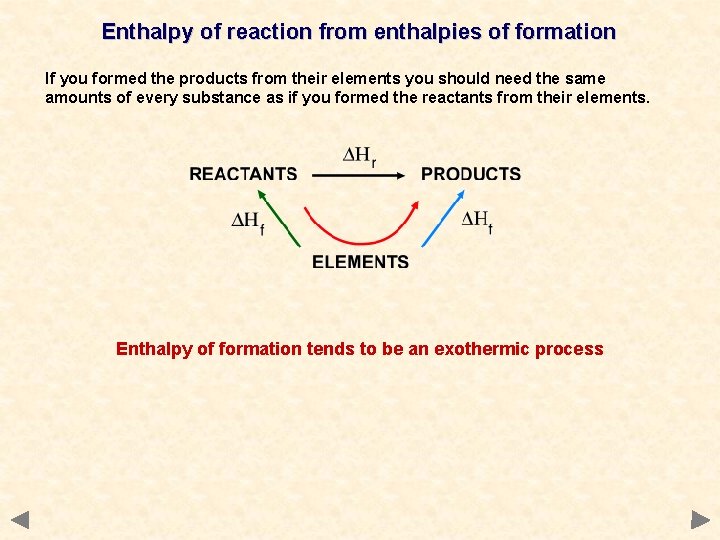
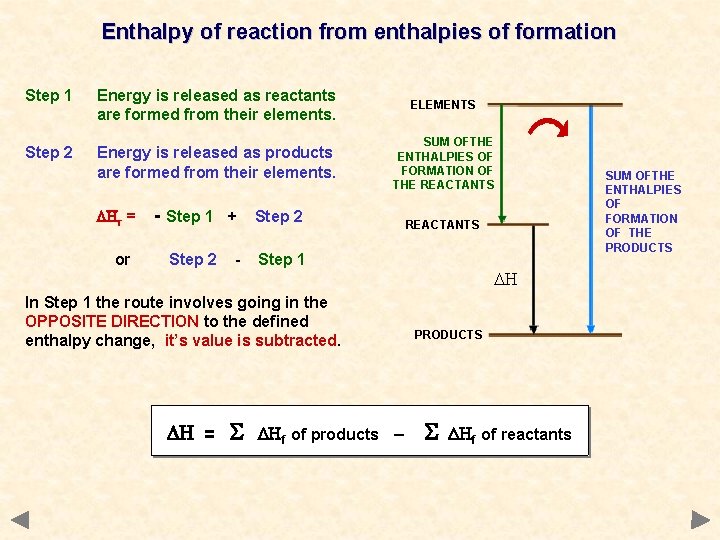
Enthalpy of reaction from enthalpies of formation If you formed the products from their elements you should need the same amounts of every substance as if you formed the reactants from their elements. Enthalpy of formation tends to be an exothermic process

Enthalpy of reaction from enthalpies of formation Step 1 Energy is released as reactants are formed from their elements. ELEMENTS Step 2 Energy is released as products are formed from their elements. SUM OFTHE ENTHALPIES OF FORMATION OF THE REACTANTS DHr = or - Step 1 + Step 2 - Step 1 In Step 1 the route involves going in the OPPOSITE DIRECTION to the defined enthalpy change, it’s value is subtracted. DH = DHf of products – REACTANTS DH PRODUCTS DHf of reactants SUM OFTHE ENTHALPIES OF FORMATION OF THE PRODUCTS

Enthalpy of reaction from enthalpies of formation Sample calculation Calculate the standard enthalpy change for the following reaction, given that the standard enthalpies of formation of water, nitrogen dioxide and nitric acid are -286, +33 and -173 k. J mol-1 respectively; the value for oxygen is ZERO as it is an element 2 H 2 O(l) DH = + 4 NO 2(g) + O 2(g) DHf of products – ———> 4 HNO 3(l) DHf of reactants By applying Hess’s Law. . . The Standard Enthalpy of Reaction DH°r will be. . . PRODUCTS REACTANTS [ 4 x DHf of HNO 3 ] minus DH°r = 4 x (-173) - [ (2 x DHf of H 2 O) + (4 x DHf of NO 2) + (1 x DHf of O 2) ] 2 x (-286) ANSWER = - 252 k. J + 4 x (+33) + 0

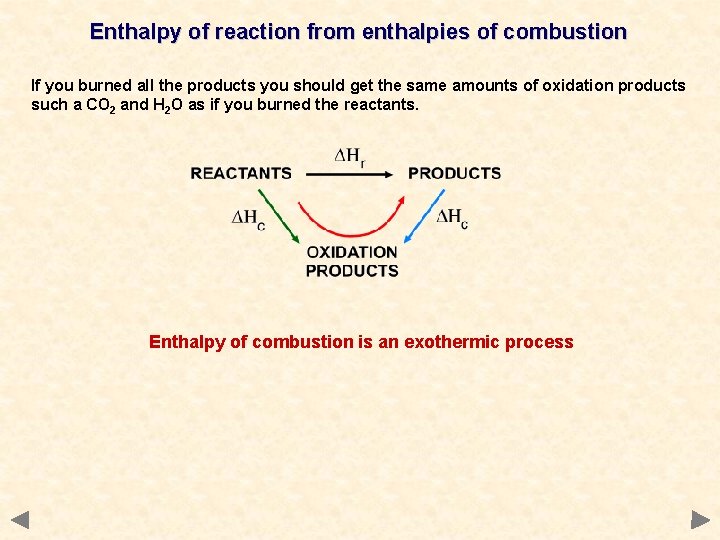
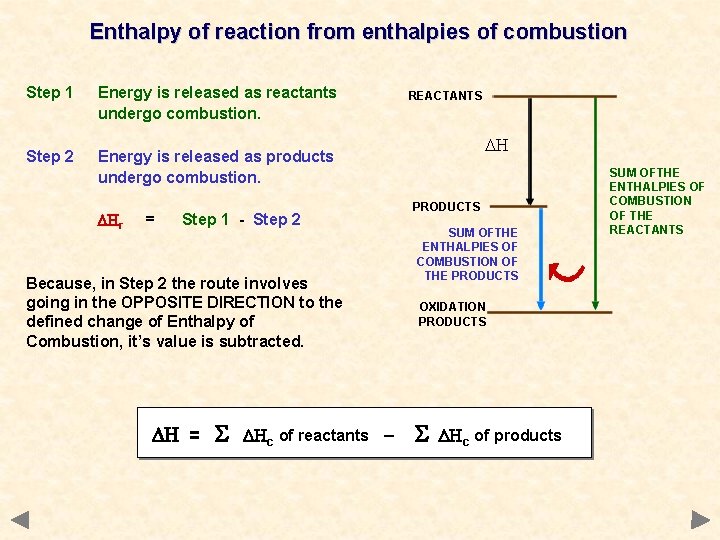
Enthalpy of reaction from enthalpies of combustion If you burned all the products you should get the same amounts of oxidation products such a CO 2 and H 2 O as if you burned the reactants. Enthalpy of combustion is an exothermic process

Enthalpy of reaction from enthalpies of combustion Step 1 Energy is released as reactants undergo combustion. Step 2 Energy is released as products undergo combustion. DHr = Step 1 - Step 2 Because, in Step 2 the route involves going in the OPPOSITE DIRECTION to the defined change of Enthalpy of Combustion, it’s value is subtracted. DH = DHc of reactants – REACTANTS DH PRODUCTS SUM OFTHE ENTHALPIES OF COMBUSTION OF THE PRODUCTS OXIDATION PRODUCTS DHc of products SUM OFTHE ENTHALPIES OF COMBUSTION OF THE REACTANTS

Enthalpy of reaction from enthalpies of combustion Sample calculation Calculate the standard enthalpy of formation of methane; the standard enthalpies of combustion of carbon, hydrogen and methane are -394, -286 and -890 k. J mol -1. C(graphite) DH = + 2 H 2(g) DHc of reactants – ———> CH 4(g) DHc of products By applying Hess’s Law. . . The Standard Enthalpy of Reaction DH°r will be. . . REACTANTS PRODUCTS [ (1 x DHc of C) + (2 x DHc of H 2) ] DH°r = 1 x (-394) + 2 x (-286) minus - ANSWER = - 76 k. J mol-1 [ 1 x DHc of CH 4] 1 x (-890)

MEASURING ENTHALPY CHANGES Calorimetry involves the practical determination of enthalpy changes usually involves heating (or cooling) known amounts of water is heated up reaction is EXOTHERMIC water cools down reaction is ENDOTHERMIC Calculation The energy required to change the temperature of a substance can be calculated using. . . q = m x c x DT where q m c DT = = heat energy mass Specific Heat Capacity change in temperature k. J kg k. J K -1 kg -1 [ water is 4. 18 ] K

MEASURING ENTHALPY CHANGES Calorimetry involves the practical determination of enthalpy changes usually involves heating (or cooling) known amounts of water is heated up reaction is EXOTHERMIC water cools down reaction is ENDOTHERMIC Calculation The energy required to change the temperature of a substance can be calculated using. . . q = m x c x DT where Example q m c DT = = heat energy mass Specific Heat Capacity change in temperature k. J kg k. J K -1 kg -1 [ water is 4. 18 ] K On complete combustion, 0. 18 g of hexane raised the temperature of 100 g water from 22°C to 47°C. Calculate its enthalpy of combustion. Heat absorbed by the water (q) = 0. 1 x 4. 18 x 25 = 10. 45 k. J Moles of hexane burned = mass / Mr = 0. 18 / 86 = 0. 00209 Enthalpy change = heat energy / moles ANS = 10. 45 / 0. 00209 = 5000 k. J mol -1

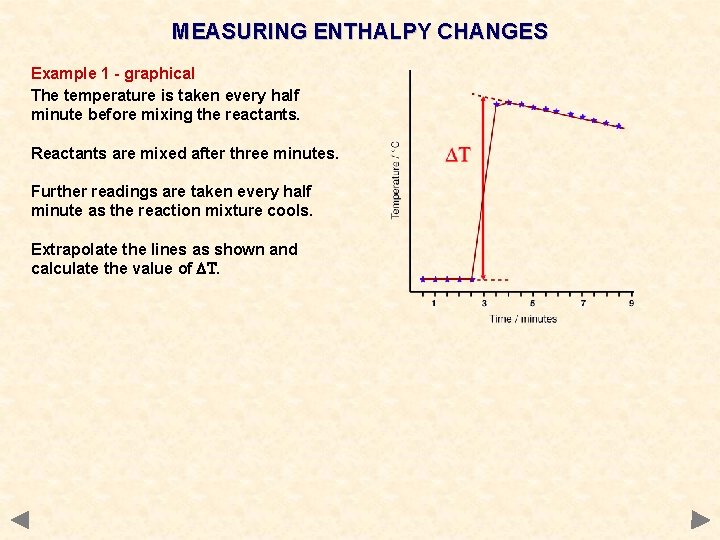
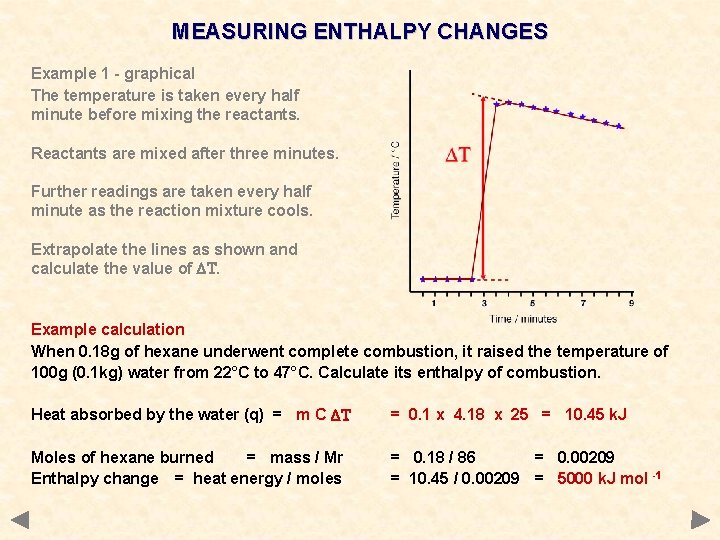
MEASURING ENTHALPY CHANGES Example 1 - graphical The temperature is taken every half minute before mixing the reactants. Reactants are mixed after three minutes. Further readings are taken every half minute as the reaction mixture cools. Extrapolate the lines as shown and calculate the value of DT.

MEASURING ENTHALPY CHANGES Example 1 - graphical The temperature is taken every half minute before mixing the reactants. Reactants are mixed after three minutes. Further readings are taken every half minute as the reaction mixture cools. Extrapolate the lines as shown and calculate the value of DT. Example calculation When 0. 18 g of hexane underwent complete combustion, it raised the temperature of 100 g (0. 1 kg) water from 22°C to 47°C. Calculate its enthalpy of combustion. Heat absorbed by the water (q) = m C DT = 0. 1 x 4. 18 x 25 = 10. 45 k. J Moles of hexane burned = mass / Mr Enthalpy change = heat energy / moles = 0. 18 / 86 = 0. 00209 = 10. 45 / 0. 00209 = 5000 k. J mol -1

MEASURING ENTHALPY CHANGES Example 2 25 cm 3 of 2. 0 M HCl was added to 25 cm 3 of 2. 0 M Na. OH in an insulated beaker. The initial temperature of both solutions was 20°C. The highest temperature reached by the solution was 33°C. Calculate the Molar Enthalpy of Neutralisation. [The specific heat capacity (c) of water is 4. 18 k. J K -1 kg -1] Na. OH + HCl ——> Na. Cl + H 2 O

MEASURING ENTHALPY CHANGES Example 2 25 cm 3 of 2. 0 M HCl was added to 25 cm 3 of 2. 0 M Na. OH in an insulated beaker. The initial temperature of both solutions was 20°C. The highest temperature reached by the solution was 33°C. Calculate the Molar Enthalpy of Neutralisation. [The specific heat capacity (c) of water is 4. 18 k. J K -1 kg -1] Na. OH + Temperature rise (DT) Volume of resulting solution= Equivalent mass of water (density is 1 g per cm 3) Heat absorbed by the water (q) HCl ——> Na. Cl = 306 K – 293 K 25 + 25 = 50 cm 3 = 50 g = m x c x DT = + H 2 O = = 13 K 0. 05 dm 3 = 0. 05 kg 0. 05 x 4. 18 x 13 = 2. 717 k. J

MEASURING ENTHALPY CHANGES Example 2 25 cm 3 of 2. 0 M HCl was added to 25 cm 3 of 2. 0 M Na. OH in an insulated beaker. The initial temperature of both solutions was 20°C. The highest temperature reached by the solution was 33°C. Calculate the Molar Enthalpy of Neutralisation. [The specific heat capacity (c) of water is 4. 18 k. J K -1 kg -1] Na. OH + Temperature rise (DT) Volume of resulting solution= Equivalent mass of water (density is 1 g per cm 3) HCl ——> Na. Cl + = 306 K – 293 K 25 + 25 = 50 cm 3 = 50 g H 2 O = = 13 K 0. 05 dm 3 = 0. 05 kg Heat absorbed by the water (q) = m x c x DT = Moles of HCl reacting Moles of Na. OH reacting Moles of water produced = = 2 x Enthalpy change per mol (DH) = heat energy / moles of water 0. 05 x 4. 18 x 13 = 2. 717 k. J 25/1000 = = = 54. 34 k. J mol -1 0. 05 mol = 2. 717 / 0. 05
 Change in enthalpy formula thermodynamics
Change in enthalpy formula thermodynamics Thermodynamics enthalpy of reaction and hess's law
Thermodynamics enthalpy of reaction and hess's law Cp thermodynamics
Cp thermodynamics 17.2 measuring and expressing enthalpy changes answers
17.2 measuring and expressing enthalpy changes answers Communicating enthalpy changes
Communicating enthalpy changes Calculation of enthalpy
Calculation of enthalpy Measuring and expressing enthalpy changes
Measuring and expressing enthalpy changes Examples of chemical change
Examples of chemical change Changes in latitudes, changes in attitudes meaning
Changes in latitudes, changes in attitudes meaning Nutrients and their functions table
Nutrients and their functions table Research methodology contents
Research methodology contents Sound contents
Sound contents Anterior mediastinum
Anterior mediastinum Styloid apparatus
Styloid apparatus Febrile non hemolytic transfusion reaction
Febrile non hemolytic transfusion reaction Define use case
Define use case M
M Quad origin
Quad origin Contents of carotid sheath
Contents of carotid sheath Table of contents background
Table of contents background Noble samn
Noble samn Contents of air pollution
Contents of air pollution Site:slidetodoc.com
Site:slidetodoc.com Company profile table of contents
Company profile table of contents Anterior mediastinum contents
Anterior mediastinum contents Nike blue ocean strategy
Nike blue ocean strategy Sas contents
Sas contents Table of contents science
Table of contents science Contents
Contents Persepolis table
Persepolis table Table of contents error
Table of contents error What is the perineum and where is it located
What is the perineum and where is it located Pericardium and mediastinum
Pericardium and mediastinum Spermatic cord contents rule of 3's
Spermatic cord contents rule of 3's Planetary systems
Planetary systems