Entanglement in Quantum Critical Phenomena Holography and Gravity

Entanglement in Quantum Critical Phenomena, Holography and Gravity Dmitri V. Fursaev Joint Institute for Nuclear Research Dubna, RUSSIA hep-th/0602134 hep-th/0606184 Banff, July 31, 2006

gravity - quantum information condensed matter finding entanglement entropy in spin chains near a critical point finding a minimal surface in a curved space one dimension higher

plan of the talk ● quantum entanglement in 2 D critical phenomena and CFT’s ● geometrical structure of entanglement entropy ● gravitational coupling in quantum gravity and entanglement entropy ● new gravity analogs in condensed matter systems (applications) ● “holographic formula” for entanglement entropy (in QFT’s dual to Ad. S gravity)

Quantum Entanglement Quantum state of particle « 1» cannot be described independently from particle « 2» (even for spatial separation at long distances)

measure of entanglement - entropy of entanglement density matrix of particle « 2» under integration over the states of « 1» « 2» is in a mixed state when information about « 1» is not available S – measures the loss of information about “ 1” (or “ 2”)

Ising spin chains off-critical regime at large N critical regime

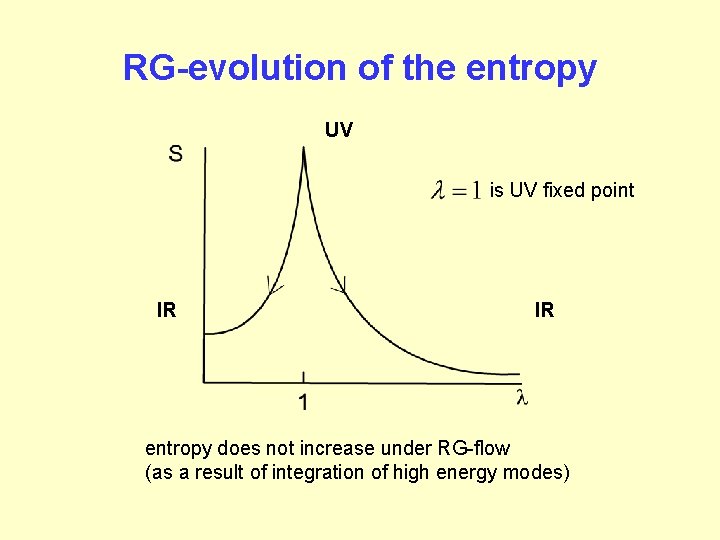
RG-evolution of the entropy UV is UV fixed point IR IR entropy does not increase under RG-flow (as a result of integration of high energy modes)

Explanation Near the critical point the Ising model is equivalent to a 2 D quantum field theory with mass m proportional to At the critical point it is equivalent to a 2 D CFT with 2 massless fermions each having the central charge 1/2

Entanglement in 2 D models: analytical results ground state entanglement on an interval Calabrese, Cardy hep-th/0405152 is the length of massive case: massless case: a is a UV cutoff

analytical results (continued) is the length of ground state entanglement for a system on a circle system at a finite temperature

effective action and geometrical structure of entanglement entropy - “partition function” -effective action is defined on manifolds with cone-like singularities - “inverse temperature”

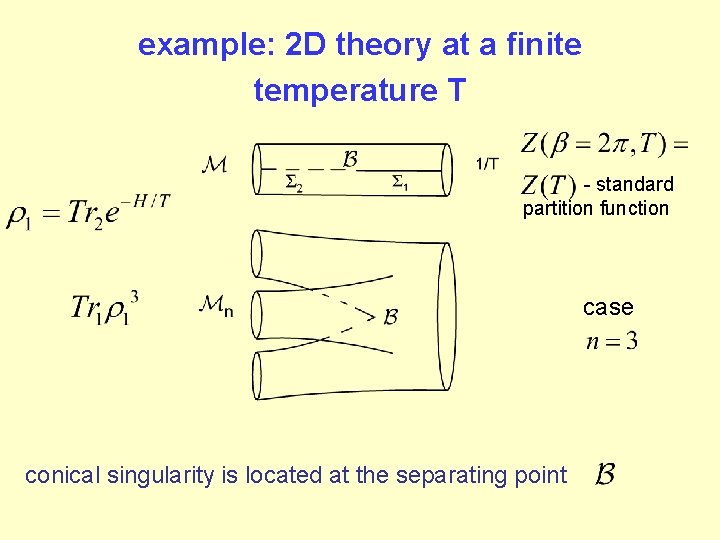
example: 2 D theory at a finite temperature T - standard partition function case conical singularity is located at the separating point

effective action on a manifold with conical singularities is the gravity action (even if the manifold is locally flat) curvature at the singularity is non-trivial: derivation of entanglement entropy in a flat space has to do with gravity effects!

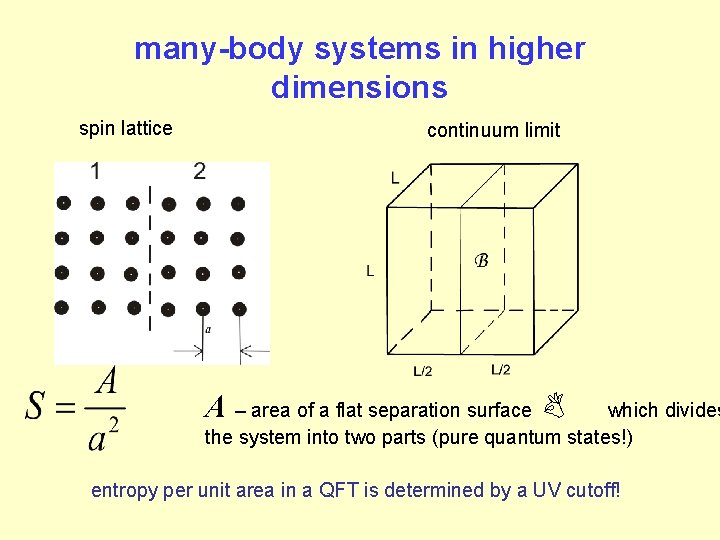
many-body systems in higher dimensions spin lattice continuum limit A – area of a flat separation surface B which divides the system into two parts (pure quantum states!) entropy per unit area in a QFT is determined by a UV cutoff!

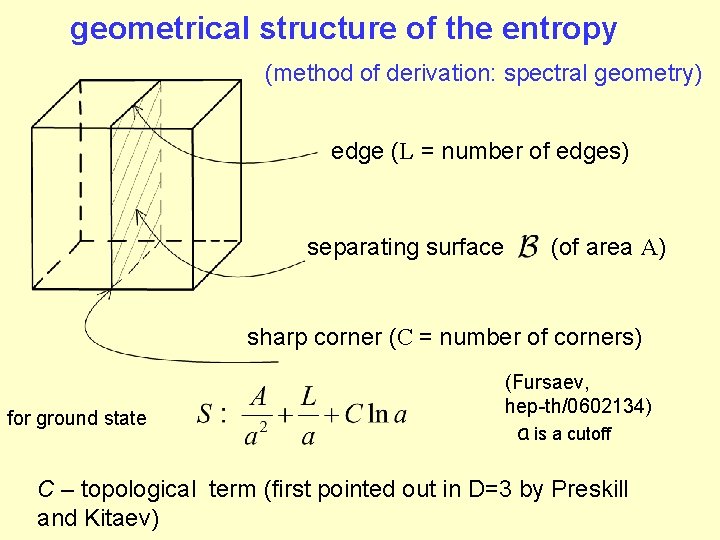
geometrical structure of the entropy (method of derivation: spectral geometry) edge (L = number of edges) separating surface (of area A) sharp corner (C = number of corners) for ground state (Fursaev, hep-th/0602134) a is a cutoff C – topological term (first pointed out in D=3 by Preskill and Kitaev)

gravitational coupling - gravitational force between two bodies is determined by the microscopical properties of a fundamental theory

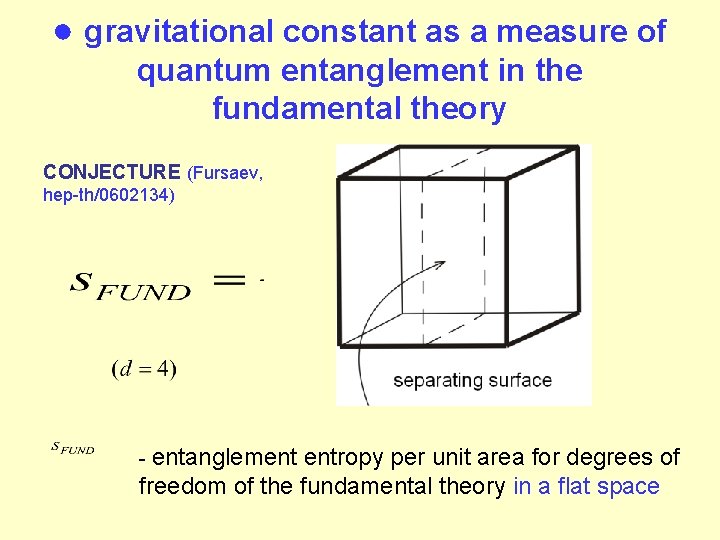
● gravitational constant as a measure of quantum entanglement in the fundamental theory CONJECTURE (Fursaev, hep-th/0602134) - entanglement entropy per unit area for degrees of freedom of the fundamental theory in a flat space

arguments: ● entropy density is determined by UV-cutoff ● the conjecture is valid for area density of the entropy of black holes ● entanglement entropy can be derived form the effective gravity action ● entropy in QFT’s which admit Ad. S duals

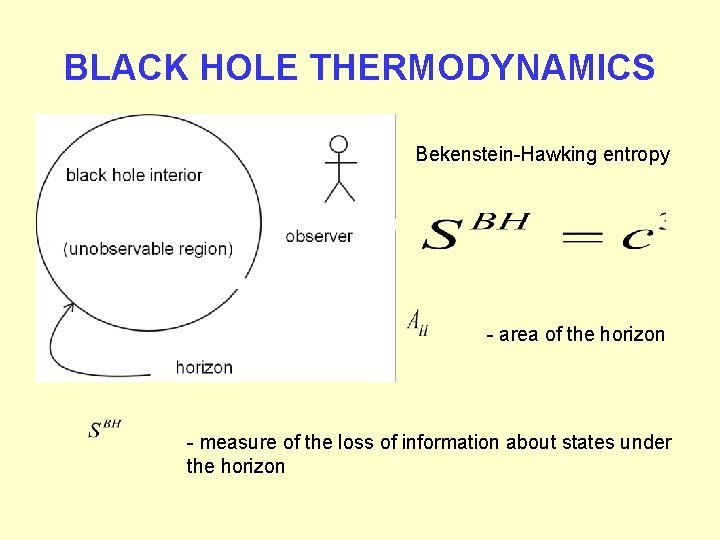
BLACK HOLE THERMODYNAMICS Bekenstein-Hawking entropy - area of the horizon - measure of the loss of information about states under the horizon

some references: ● black hole entropy as the entropy of entanglement (Srednicki 93, Sorkin et al 86) ● iduced gravity (Sakharov 68) as a condition (Jacobson 94, Frolov, Fursaev, Zelnikov 96) ● application to de Sitter horizon (Hawking, Maldacena, Strominger 00) ● entropy of certain type black holes in string theory as the entanglement entropy in 2 - and 3 - qubit systems (Duff 06, Kallosh & Linde 06) our conjecture : ● yields the value for the fundamental entropy in flat space in terms of gravity coupling ● horizon entropy is a particular case

● applications: new gravity analogs in condensed matter systems In condensed matter systems one can define an effective gravity constant where is the ground state entanglement entropy per unit area Requirements: ● lattice models (cutoff) ● second order phase transition ● description in terms of a massive QFT near the critical point Advantage: one does not need to introduce effective metric in the system

theories with extra dimensions the conjecture should hold in higher dimensions: fundamental entanglement entropy per unit area of the separating surface is is the higher-dimensional gravitational coupling What is the separating surface ● Kaluza-Klein-like theories: in higher dimensions? is - space of extra dimensions ● brane-world models (only gravity is higher dimensional): extension of the separating surface to higher dimensions has to be determined by the dynamical gravity equations in the bulk

Holographic Formula for the Entropy Ryu and Takayanagi, hep-th/0603001, 0605073 CFT which admit a dual description in terms of the Anti-de Sitter (Ad. S) gravity one dimension higher Let be the extension of the separating surface 1) in d-dim. CFT is a minimal surface in (d+1) dimensional Ad. S space 2) “holographic formula” holds: is the area of is the gravity coupling in Ad. S

the holographic formula enables one to compute entanglement entropy in strongly coupled theories by using geometrical methods

example in d=2: CFT on a circle - Ad. S radius A is the length of the geodesic in Ad. S - UV cutoff -holographic formula reproduces the entropy for a ground state entanglement - central charge in d=2 CFT

Sketch of the proof of the holographic formula Fursaev, hep-th/0606184 -Ad. S/CFT representation for CFT partition function (with specific boundary conditions) (3 D Ad. S / 2 D CFT) is (a conformal) boundary of

the proof (continued) in semiclassical approximation there are conical singularities in the bulk located on extremality of the action requires be a minimal surface

consequences • possibility to consider entropy in stationary but not static theories (Riemannian sections) • choice of the minimal surface in case of several options • theories with different phases and phase transitions • higher-curvature corrections in the bulk • entropy in brane-world models (Randall and Sundrum)

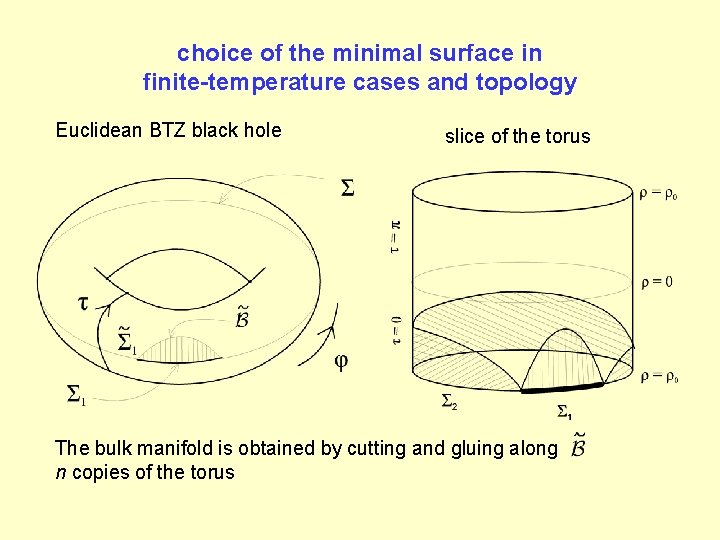
choice of the minimal surface in finite-temperature cases and topology Euclidean BTZ black hole slice of the torus The bulk manifold is obtained by cutting and gluing along n copies of the torus

Summary - Entanglement and critical phenomena in condensed matter systems (d=2, . . . ) - Entanglement in quantum gravity: relation to gravity coupling in a fundamental theory - New gravity analogs in condensed matter (lattice models) - “Holographic” representation of entanglement entropy: geometrical way of computation + new ideas