Entanglement and Quantum Phase Transition in Matrix Product

Entanglement and Quantum Phase Transition in Matrix Product Systems S. Alipour Department of Physics, Sharif University of Technology Tehran, Iran International Iran Conference on Quantum Information, 7 -10 Sept. 2007, Kish Island 0

Outline • Why do we study matrix product states? • Matrix product formalism (MPF) • An example: Spin-one chain 1

From the condensed matter point of view The starting point for studying many body systems is a given Hamiltonian which captures all interactions in the system The basic problem: Finding the Ground state (GS) and low lying states of H Finding the Physical properties of the system at low temperatures T 0 Thermal fluctuations Quantum phase transitions (QPT)

From the condensed matter point of view Physical properties of interest: • • Critical exponents Correlation length N-point functions … Unfortunately solving these problems is extremely difficult. There are only a few rare examples: • XX chain (free fermion) • Heisenberg chain (Bethe ansatz) 3

From the quantum information point of view The emphasis is on the properties of given states. A very important property: Entanglement between particles The state which has enough amount of multi-partite entangleme can be used as an initial state in a quantum computer. The basic problem: To find a physical system (H) whose GS is this state. 4

MPF as a promising connection point of condensed matter physics and quantum information theory Condensed Matter Physics Quantum Information Theory Matrix Product States 5

Matrix Product Formalism … 1 2 3 The state of the chain This state is called a MPS are D-dimensional matrices Ais are not unique: N

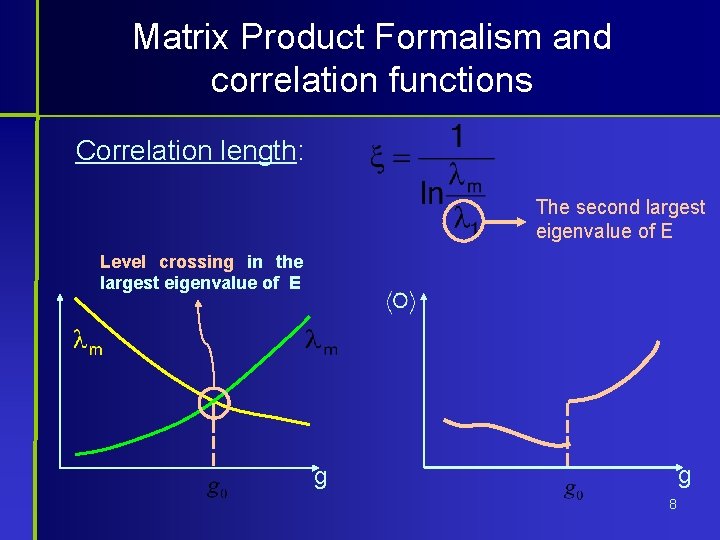
Matrix Product Formalism and correlation functions This matrix has an important role in recognizing QPT In thermodynamic limit we have: The largest eigenvalue of E 7

Matrix Product Formalism and correlation functions Correlation length: The second largest eigenvalue of E Level crossing in the largest eigenvalue of E g g 8

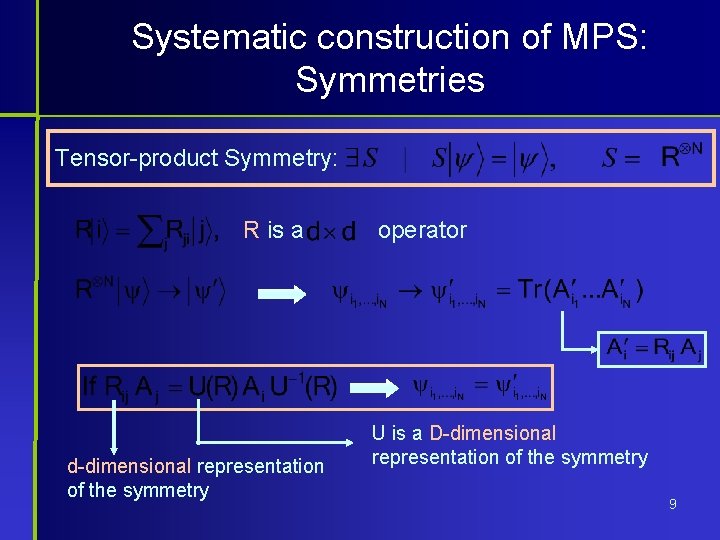
Systematic construction of MPS: Symmetries Tensor-product Symmetry: R is a d-dimensional representation of the symmetry operator U is a D-dimensional representation of the symmetry 9

Systematic construction of MPS: Symmetries In terms of the generators: • Rotational symmetry around z-axis: • Parity: The state is the same whether we look at the chain from left or right. 10

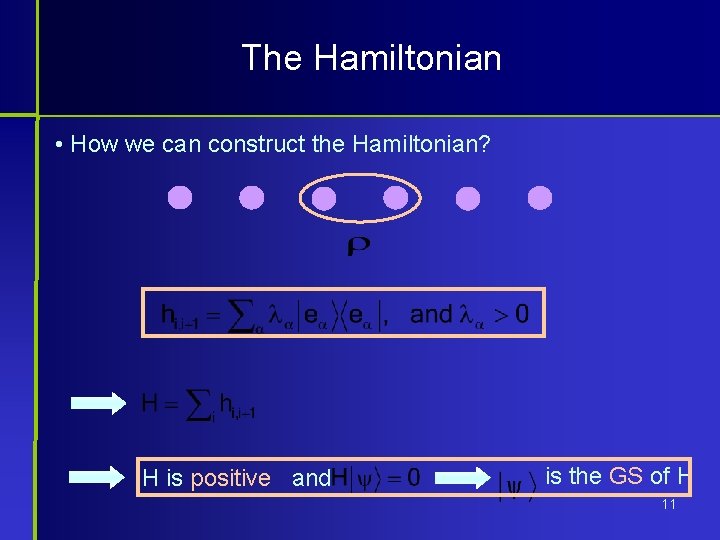
The Hamiltonian • How we can construct the Hamiltonian? H is positive and is the GS of H 11

Example: A spin-one chain I. Affleck et al. PRL (1987) Full rotational symmetry Rotation around z-axis only

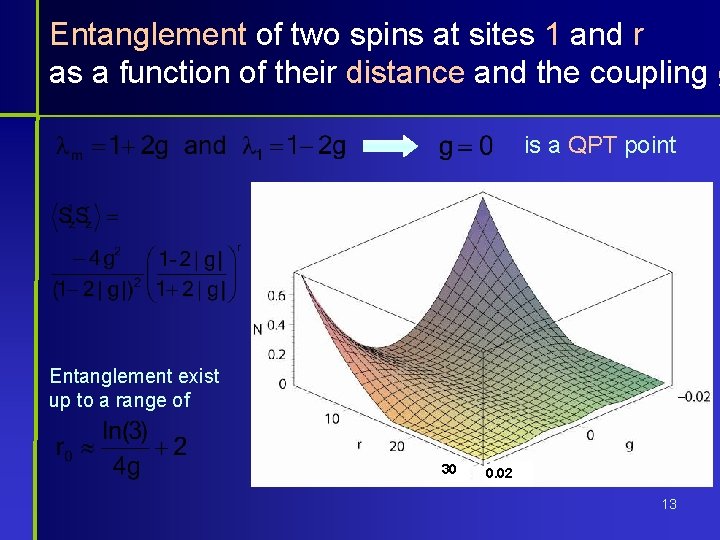
Entanglement of two spins at sites 1 and r as a function of their distance and the coupling g is a QPT point Entanglement exist up to a range of 30 0. 02 13

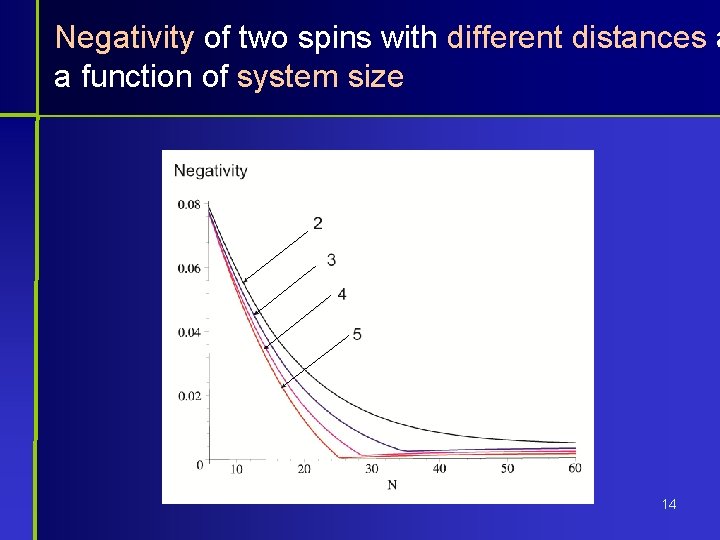
Negativity of two spins with different distances a a function of system size 14

Negativity of two spins as a function of their distance for a ring of size N=40 15

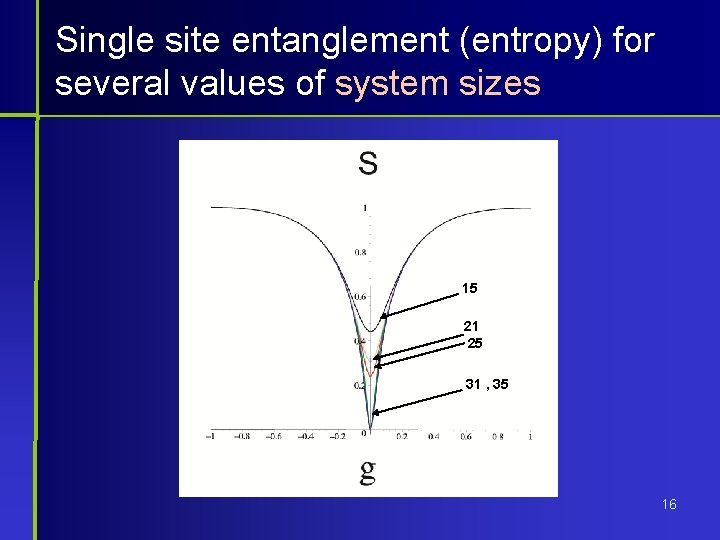
Single site entanglement (entropy) for several values of system sizes 15 21 25 31 , 35 16

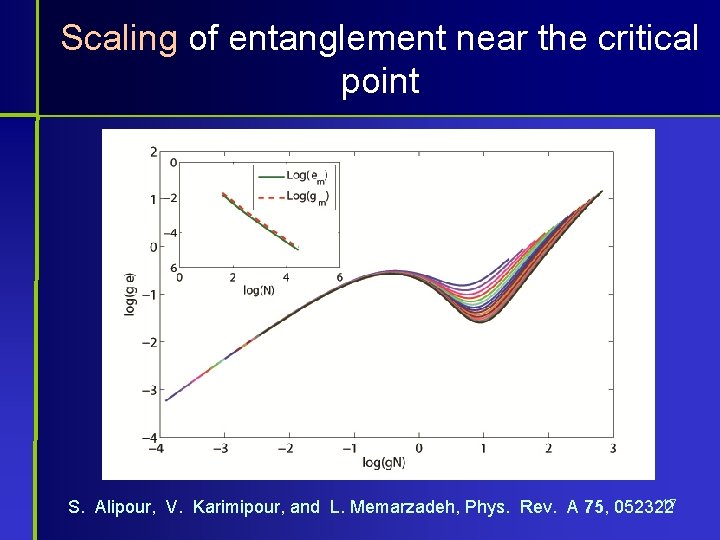
Scaling of entanglement near the critical point 17 S. Alipour, V. Karimipour, and L. Memarzadeh, Phys. Rev. A 75, 052322

Summary 1. We have shown how to systematically construct stats which has continuous or distinct symmetries. 2. We have shown that how entanglement between two particles shows scaling behavior.

Large r Correlation length: 19